基于电压参量的新型谐波补偿策略研究

范建兵，樊飞强2，董昱廷，闵令民

(1.国网新疆电力有限公司经济技术研究院，新疆 乌鲁木齐 830000; 2.国网新疆电力公司哈密电力公司，新疆 哈密 839000)

1 引言

配电网中非线性电力电子器件比重增大，给人们的生活带来方便，但同时导致电网的谐波含量增多[1-3]。目前普遍采用有源滤波器来补偿谐波，但因算法的原因造成检测精度和检测速度相矛盾，为解决这一问题，本文提出一种改进的基于谐波电压的检测算法，并结合仿真验证算法的有效性[4]。

2 有源滤波器谐波补偿策略

谐波补偿的原理如图1(a)所示，将总电流分为基波电流I1和谐波电流Ih。采样信号取自总电流Is，其中：

Is=I1+Ih

(1)

(2)

根据检测出的Ih控制APF发出与之反相的补偿电流[5-7]。

通常APF的参考电流IL,h采样自IL(如图1(a)所示)。通过算法运算后控制补偿装置输出补偿电流IF[8]。具体原理如图2所示。

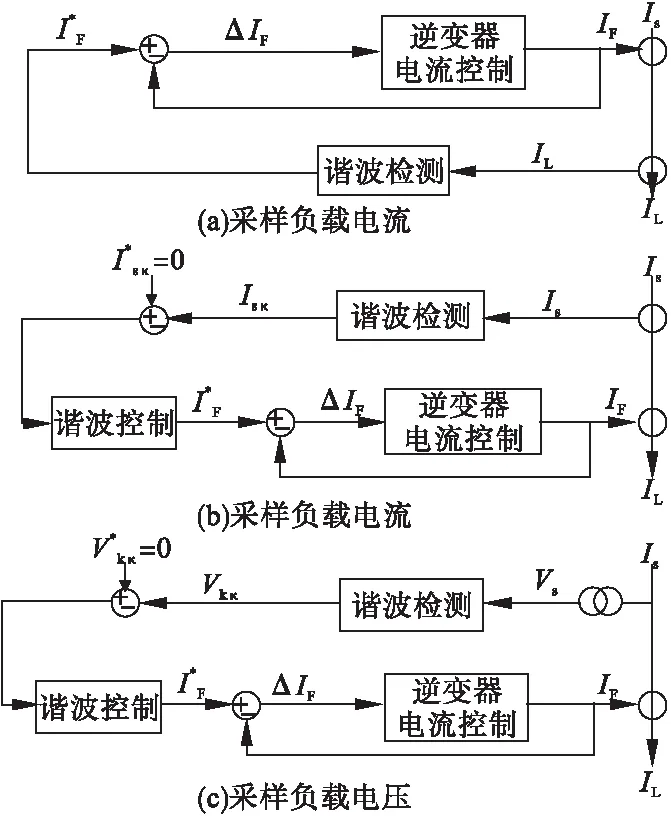
图1 APF工作原理

滤波器输出的补偿电流值是：

(3)

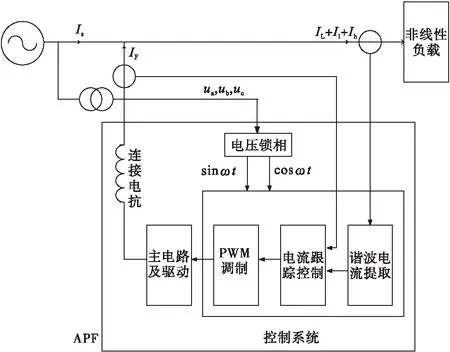
图2 传统APF控制策略

本文采用一种从电压采集信号的方法，通过谐波电压来控制补偿装置的输出值。再通过静止坐标下的广义积分产生参考电流IF*。图1(c)给出过程[9]。

具体环节如图3所示，包含三部分：谐波检测、谐波控制器(SGI)、锁相环装置(SRF-PLL)[10]。

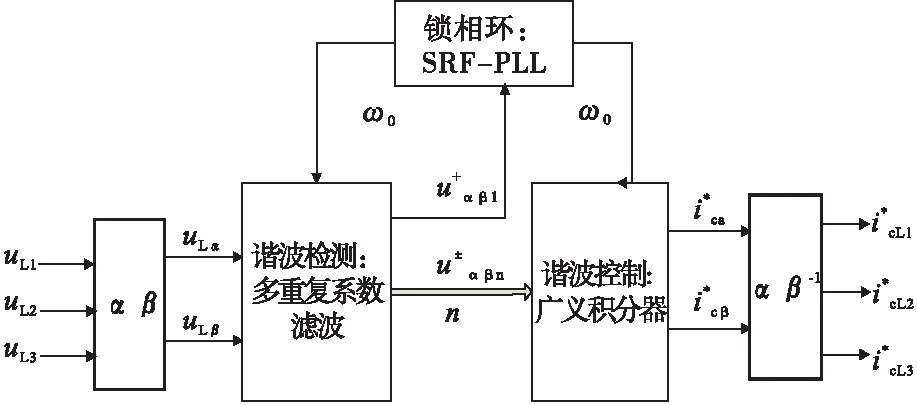
图3 采样自电压的谐波补偿的控制策略图

3 采样自电压的谐波补偿策略

文献[10]给出一种分离各次谐波电压的方法，如图4(a)所示，通过这一结构将输入电压的各次谐波分离。再通过使用静止坐标系下的克拉克变换形成一个正交的两相α-β系统(如图4(b))。式(6)～(8)给出不同频率参量值，k代表频次：

(6)

滤波器的传递函数和输入信号分别是：

其中：

(7)

(8)

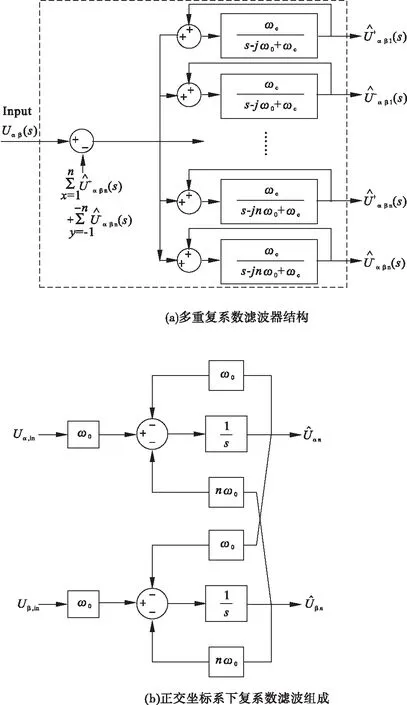
图4 传递函数和复系数滤波器组成

改变PI控制器的参数以对应不同频次谐波，组合到一起构成谐波控制器。式(9)给出了对应k次谐波的传递函数：

(9)

对图4中输出的采样电压作为图5的输入信号，通过积分运算后得到补偿电流参考值IF*：

(10)

其中Kp和Ki是比例积分增益系数，Uh，x是所选择的谐波电压。

在克拉克坐标变换的基础上由复系数谐波检测器计算谐波电压，SGI控制器的运算量变得非常少，同时将耦合的各次谐波分离计算出各自的补偿参量，极大的提升了补偿的精度。

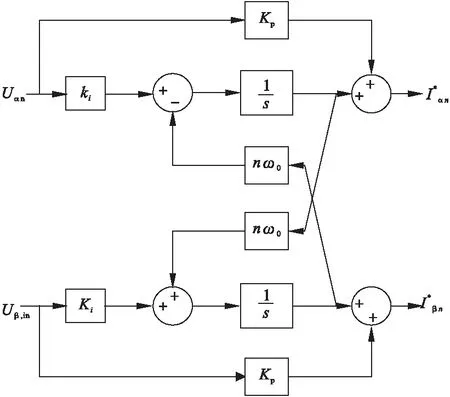
图5 静止坐标系下的广义积分器

表1 不同频次的控制器参数值

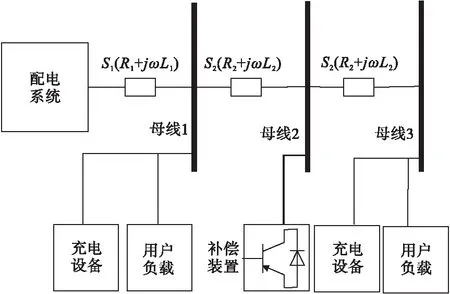
图6 模拟测试系统

图6中，通过模拟配电网环境来进行测试。考虑补偿的整体效果，将补偿装置接到母线2上，同时各母线并联谐波负载产生谐波。

4 仿真实验及结果分析

通过MATLAB 中SimPower Systems Tool box来模拟测试环境。为了形成对比，检测补偿前后各段的谐波含有率THDu，如表3所示。图7给出了电网的总电流及补偿电流值，可以看出补偿装置仅有0.1s的延时，补偿电流注入后，谐波明显减少。

图8所示为各频次谐波分离的结果。本检测方法可有效分离各频次的谐波电压。

图9所示频谱图说明了本文所提出的补偿策略的补偿效果，补偿装置安装处母线2的谐波几乎被完全补偿。并给出母线1和母线3补偿前后的谐波含量对比值，说明本文提出的谐波补偿策略补偿效果明显。

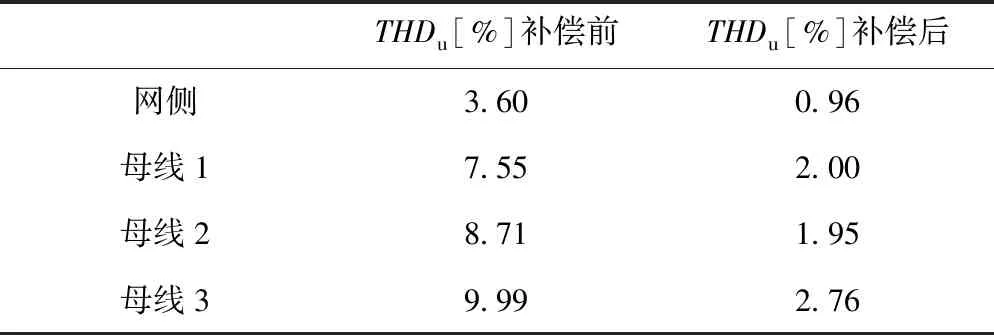
表3 谐波含量对比

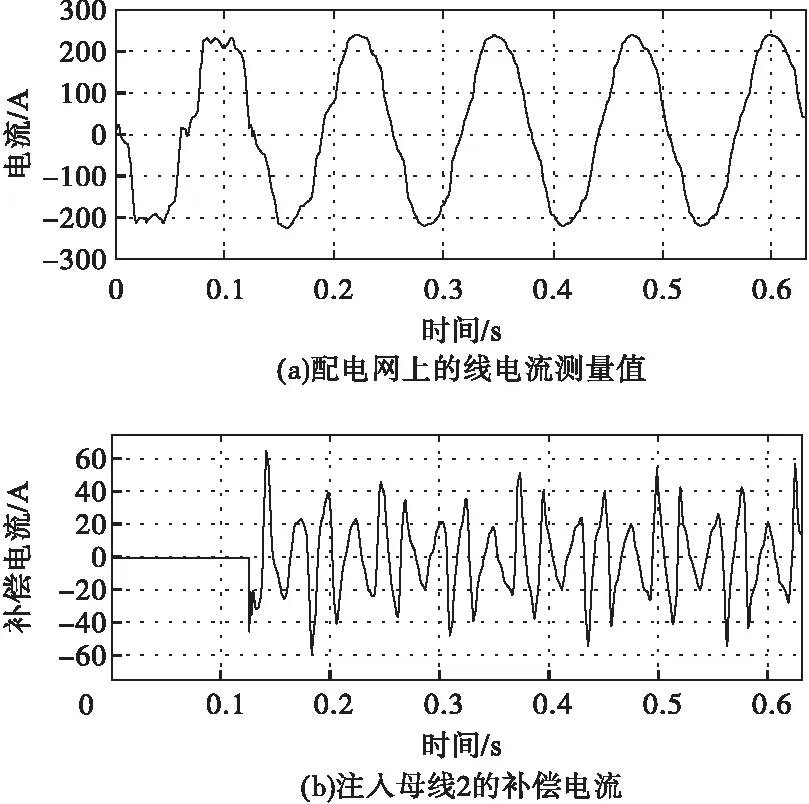
图7

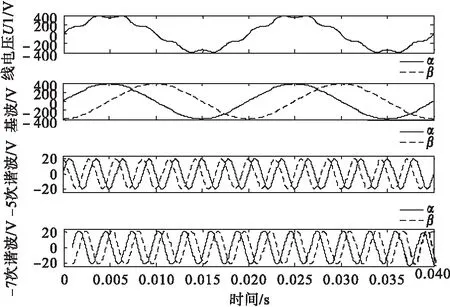
图8 不同频次谐波分离结果

5 结论

本文采用一种新型谐波补偿方法，滤波器采样自谐波电压，对电压谐波分离后输入到新型的积分器中，通过对其积分生成补偿电流信号。当电网处于暂态时，该系统仍能准确检测谐波电压，为控制滤波器提供准确参考值。应用于静止坐标系下的新型积分器运算简单，极大的提升检测效率。最后，通过仿真模型验证了这一方法的正确性。补偿后谐波含量明显降低。

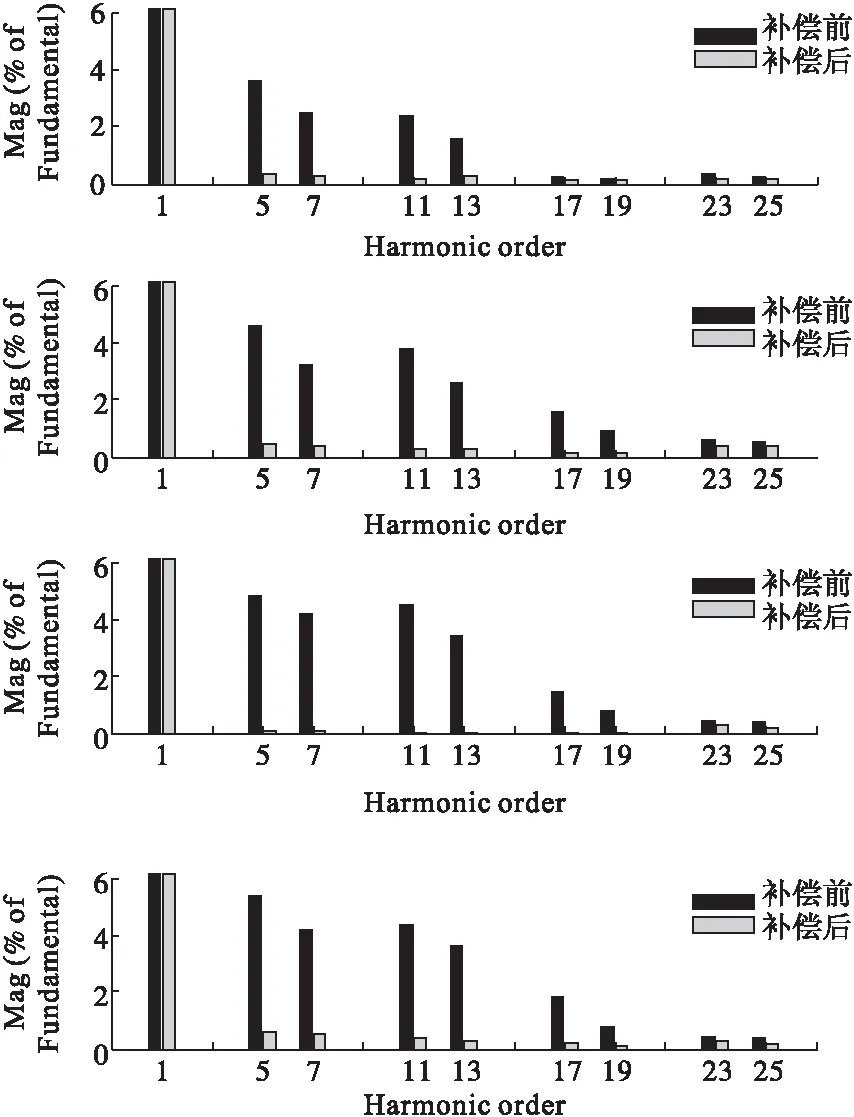
图9 测量点的谐波含量