微网中电动汽车有序充放电的粒子群优化控制

(广西大学电气工程学院，广西 南宁 530004)

1 引言

随着全球能源问题与环境危机的日益突出，以光伏、风电为代表的可再生分布式电源以其优越的环保性能而得到了迅速发展。这些分布式电源大多数是通过微电网的形式接入大电网，而其本身具有一定程度的随机性和波动性，使得在微电网中必须配置合适的储能系统。目前，蓄电池通常被选用为微电网的储能装置。近年来，电动汽车(Electric Vehicle，EV)作为一种“低噪音、零排放、零污染”的新型能源汽车，受到世界各国的青睐、重视与发展。电动汽车的行驶行为具有时空分散性和其充电行为则具有随机性，若其大规模渗透到电网中，给电网安全稳定运行带来新的挑战与机遇。电动汽车接入电网(Vehicle to Grid，V2G)模式的提出[1]，给未来电动汽车的发展带来了一定机遇。电动汽车的大规模发展与普及，将其接入微电网中，考虑充分利用其自身所具有的储能特性，通过双向互动的充电桩来实现电动汽车的V2G功能，以达到提高微电网的可靠性、减少储能的配置和平抑微电网中的负荷波动的目的，是可行的。

电动汽车的接入行为对配电网的稳定运行有很大的影响[2-6]，其影响主要包括电压波动、谐波电流和三相不平衡等电压质量问题、继电保护规划、负荷叠加、电网规划等问题。研究表明，电动汽车一天中有90%的时间会处于停使闲置的状态[7]，其具有移动存储电能的特性，可通过V2G方式接入微电网，并承担微电网中分布式储能的责任，保障微电网的安全稳定可靠运行，提高微电网中分布式电源的渗透率。有关电动汽车与电网运行的研究，国内外已有不少文献报道，文献[8]指出EV换电站作为储能可提高微电网的可再生能源接纳能力和可靠性，并更具有经济性；文献[9-10]建立电动汽车与可再生能源协调调度的数学模型，验证了利用电动汽车作为平抑等效负荷波动的手段的可行性；文献[11-12]以提高微电网的经济性为目标建立成本最低的能量管理模型，对比分析加入EV前后的情况。文献[13-14]通过以优化EV充电的过程为手段降低电网损耗，但是研究中并未计及EV的放电过程。不过上述的研究中均较少考虑EV的放电过程，也未根据每辆EV自身的荷电状态进行优化控制，可能会导致EV电池的过充或过放等问题的发生，影响车主的使用。

本文以小型的孤岛运行的微电网作为研究对象，其中包含光伏发电系统、传统蓄电池储能、本地负荷以及电动汽车充放电负荷等，研究电动汽车充放电的优化问题。首先，根据现有的统计数据及车主日常行为，利用蒙特卡洛方法获取电动汽车车主的充电需求。其次，依据电动汽车的充放电特性，以电动汽车充放电功率为优化变量建立相应的模型，并提出引进互相学习策略对粒子群优化算法加以改进；最后，在Matlab平台上对该算法进行编程仿真并加以应用，求出该优化模型的Pareto前沿，获得较符合实际的电动汽车充放电控制策略。

2 微电网的结构与功能

随着新能源技术的不断发展与成熟，EV、光伏发电大规模发展，它们主要通过微电网接入大电网。典型微电网结构如图1所示，结构中包含EV充放电系统、光伏发电系统、储能系统及本地基本负荷等，控制中心可以实时监控微电网的运行状态。

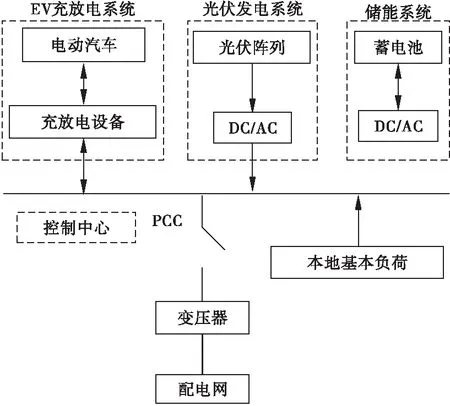
图1 典型微电网结构

2.1 光伏发电系统模型

采用贝塔分布函数描述辐照度的随机性，如式(1)所示。其中，α，β是伽马函数的形状参数，与辐照度平均值和方差的关系如式(2)和式(3)所示。

(1)

(2)

(3)

式中，f(·)为概率密度函数；r(t)为实际辐照度；rmax(t)为最大辐照度；Γ(·)为伽马函数；α，β为形状参数；μ为随机变量均值；σ2为随机变量方差。

基于辐照度的概率密度分布和光伏发电的准稳态数学模型，得到光伏发电功率波动的概率分布函数。光伏发电的出力如式(4)所示。

Ppv(t)=ηSr(t)

(4)

式中，Ppv(t)为t时刻的光伏出力；η为光电转换效率；S为光伏阵列的面积。

光伏出力的概率密度函数为：

(5)

可以根据当地典型日的光照强度和温度变化来模拟光伏发电系统的出力。

2.2 储能系统模型

储能系统主要是由传统的蓄电池组成的，不包含电动汽车的储能部分，其在微电网中可以平抑可再生能源发电的波动，增加可再生能源的利用率。蓄电池运行过程中必须满足：

Ebat(t+1)=Ebat(t)*(1-σ)+Pbat(t)

(6)

SOC(t)=(1-σ)SOC(t-1)+PbatΔt/ηEC

(7)

式中，σ为储能系统自放电率；Pbat(t)为储能系统充放电功率，Pbat(t)>0为充电，Pbat(t)<0为发电；η为充放电效率；EC为储能系统的额定容量。

2.3 电动汽车充电需求模型

2.3.1 开始充电时间的概率模型

根据参考文献[15]，获得用户最后一次结束行驶的时间数据，假定用户在最后停止行驶的时刻就开始进行充电，开始充电时间分布如图2所示。

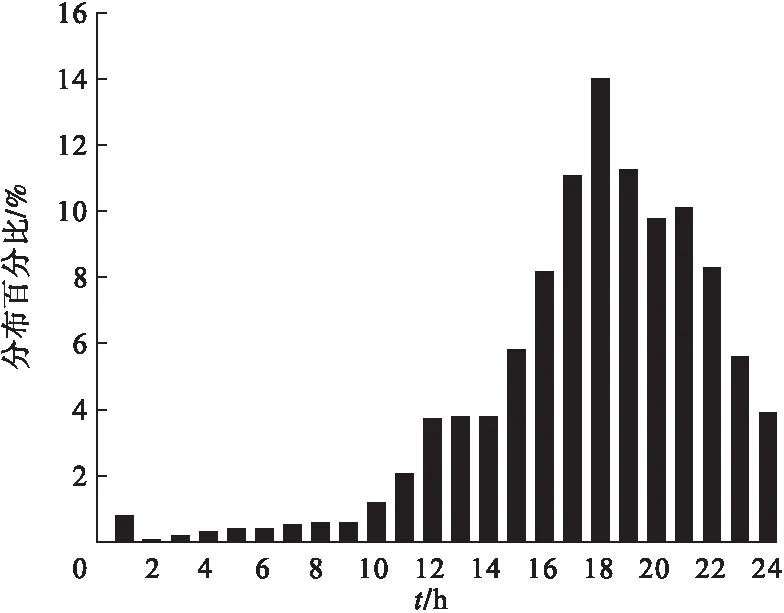
图2 电动汽车开始充电时间分布

研究表明，用户开始充电时间概率分布服从正态分布，如式(8)所示。

(8)

式中，μs=17,σs=3.3。

2.3.2 电动汽车出行特征参数

根据参考文献[15]，获得日行驶里程的数据，电动汽车日均行驶里程的分布百分比如图3所示。

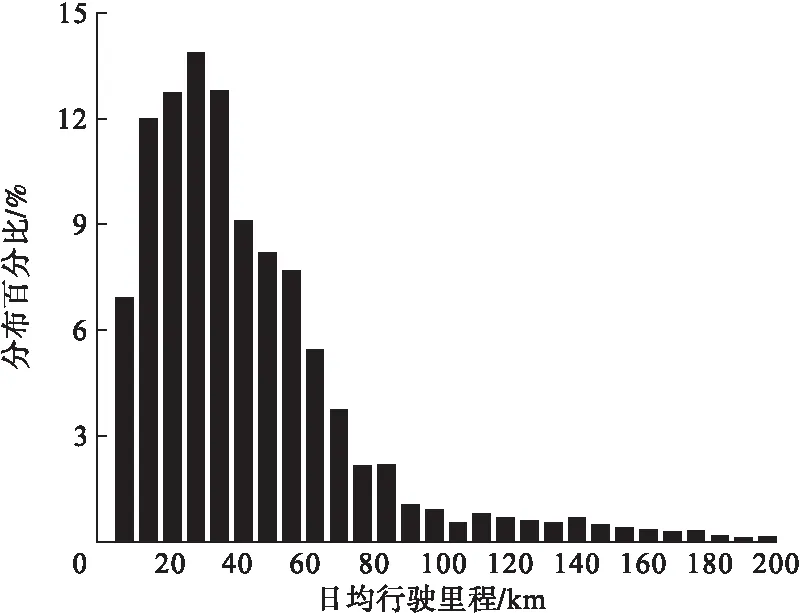
图3 电动汽车日均行驶里程分布

通过对电动汽车的日行驶里程数据进行拟合，可知其主要呈对数正态分布。关于行驶里程的概率密度函数可描述为式子(9)所示。

(9)

式中，μd为EV每天行驶里程的平均值；σd为对数正态分布的标准差；d为行驶里程。

2.3.3 电动汽车充放电负荷

电动汽车作为一种移动式储能，其接入微电网的位置和容量都具有一定程度的随机性和不确定性。本文所提出的EV充放电负荷的模型，获取步骤如下：

(1)根据单辆电动汽车的电池类型及总容量，确定电动汽车接入微电网的充放电行为特性。根据车主的出行时间和停使时间，确定电动汽车的开始充电时间。同时，根据电动汽车行驶里程、电池能耗等相关信息，确定车主充放电前一刻的荷电状态(SOC)值，可获取电动汽车一天中的充放电功率及其相应SOC变化过程。

(2)确定电动汽车接入微电网参与V2G平均时间长度和参与V2G的电动汽车总数，根据历史统计信息，预测电动汽车分布式储能允许的最大充放电功率。

(3)根据微电网的需要，以电动汽车分布式储能允许的最大充放电功率、电池约束、电网约束以及用户出行方便为约束条件制定电动汽车充放电负荷曲线。

(4)依据现有的数据，通过蒙特卡洛方法模拟得到n辆电动汽车的充放电过程，进而获取电动汽车一天不同时段的充放电负荷值。

3 微电网中电动汽车优化模型

3.1 模型概述

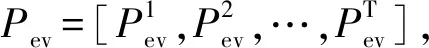
模型假设条件：(1)电动汽车属于私人所有，型号一致；(2)电动汽车在充放电的过程中不考虑动力电池的功率损耗及其寿命周期的影响。

3.2 目标函数

本文以系统的总功率波动与光伏出力差值的标准差最小为目标函数，目标函数如式子(10)所示。

(10)

(11)

Ps(t)=P(t)+Pev(t)+Pbat(t)-Ppv(t)

(12)

式中，T为一天的时长；Nk为一天中的采样点总数，即24；Pav为总负荷功率与光伏发电功率差值的平均值；Ps(t)为t时段系统的等效总负荷功率与光伏发电功率差值；P(t)为t时段系统的基本负荷功率；Pev(t)为t时段系统的电动汽车充放电功率，充电时为正，放电时为负；Ppv(t)为t时段系统的光伏发电功率；Pbat(t)为t时段系统的储能系统充放电功率。

3.3 约束条件

(1)节点电压约束：

Uimin≤Ui≤Uimax,i=1,2,…,n

(13)

式中，Ui为节点i的电压；Uimin和Uimax分别为节点电压的上限和下限。

(2)支路限流约束：

Ii≤Iimax,i=1,2,…,n

(14)

式中，Ii为节点i的电流；Iimax为节点i的电流上限。

(3)电动汽车充放电功率约束：

(15)

式中，P(t)ev,i为第i台电动汽车在时段t的充放电功率；P(t)c,max为最大充电功率；P(t)d,max为最大放电功率。

(4)储能系统约束：

(16)

式中，Pc,min和Pc,max分别为储能系统的最小和最大充电功率；Pd,min和Pd,max分别为储能系统的最小和最大放电功率；Rmin和Rmax分别为储能蓄电池的最小和最大荷电状态。

4 模型求解

4.1 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)是依托于鸟类觅食模型来寻找最优值的。PSO算法的搜索性能取决于其全局搜索和局部优化之间的平衡，这在很大程度上是与算法的控制参数有关系的，参数设置包括有粒子位置与速度的初始化、惯性因子ω的值、最大速度νmax的设定和加速常数c1与c2的值。

(17)

(18)

(19)

PSO算法具有算法简单、适应性强、搜索速度快、效率高的优点，故而在函数优化、神经网络训练、工程规划领域广泛。然而，该算法存在早熟、收敛速度慢且精度比较低、容易陷入局部最优、容易发散等缺点，导致输出结果的可靠性与准确性难以得到保证。实际应用中往往需要对其加以改进。

4.2 改进粒子群优化算法

由于粒子群多样性的丧失，使得传统PSO算法比较容易陷入到局部最优的情形，导致算法在求解复杂问题时过早收敛，最终使得寻求到的最优解并非是全局最优。针对传统PSO算法所存在的缺陷与不足，同时为了增强PSO算法的全局搜索、寻优能力和对不同优化问题的适应度，提出在传统PSO算法的基础上加以改进。本文针对孤岛运行的微电网中电动汽车有序充放电优化模型采用了学习型的粒子群优化算法。该算法将人类社会中有建设性的团队理念引入到PSO算法中，形成的一种种群之间相互学习策略的改进粒子群算法(IIL-PSO)来克服典型粒子群学习策略的多样性丧失问题。

4.3 求解步骤

采用改进粒子群算法求解微电网中电动汽车有序充放电控制问题时，其基本步骤如下。

(1)种群、参数初始化。导入全年光照、温度以及负荷数据，设置算法的基本参数，如：种群规模，粒子维数，决策变量的上下限、最大迭代次数、学习因子等参数。

(2)根据式子(20)和(21)分别确定学习种群与被学习种群、学习的概率。

(20)

Pci=0.1+0.5×(Si/Nj)5

(21)

(3)计算种群中每个粒子的适应度。各粒子的个体极值pbest为当前位置，gbest表示个数为m的pbest中适应度最高的粒子位置。

(4)如若随机概率小于等于Pci，那么按照式子(22)更新粒子群的速度，否则按照式子(23)更新速度。

(22)

(23)

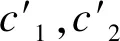
(5)按照式子(19)更新粒子位置。

(6)计算更新后粒子群的适应度，并同时更新pbest和gbest。将新粒子的适应度与各自pbest的适应度进行比较，如果优于pbest，则将优于pbest的新粒子位置作为各自新的pbest。将这些新的pbest中适应度最高的pbest与gbest适应度进行比较，如果优于gbest，则将优于gbest的适应度最高的pbest的位置作为新的gbest；否则，gbest不变。

(7)确定粒子群是否达到最大迭代次数？如果是，则输出gbest，程序结束；否则，转到步骤(4)。

5 仿真分析

5.1 仿真参数的设置

仿真参数如下：

建立如图1所示的微电网模型，单个蓄电池组的最大充放电功率为40kW，微电网中传统储能的最大容量为2MW。

(2)取某区域典型日负荷曲线为微电网的负荷。

(3)单一光伏组件在标准测试条件下，即日照强度为1000W/m2、参考温度为25℃时的最大输出功率为400W，整个微电网中光伏发电系统装机容量为3MW。选取典型日作为光伏阵列光照强度和环境温度参考值，并计算光伏出力。

(4)单辆电动汽车的电池容量为40kW·h，最大充放电功率为5kW，100km耗电量为12kW·h，不考虑电动汽车自放电率和充放电效率。

(5)考虑微电网区域的大小，假定区域内有500辆EV，其中20%的EV有接入微电网充放电的需求。EV利用双向充电机实现充放电过程，其SOC的上下限分别设置为95%和20%。

5.2 仿真结果与比较

典型光伏发电功率、负荷预测曲线如图4所示。

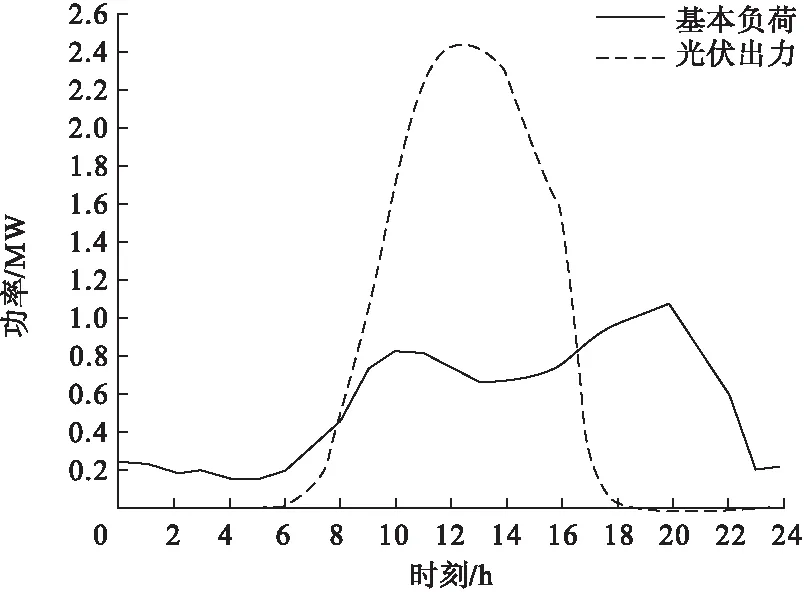
图4 典型的光伏出力与基础负荷曲线

电动汽车无序接入微电网的负荷曲线如图5所示。

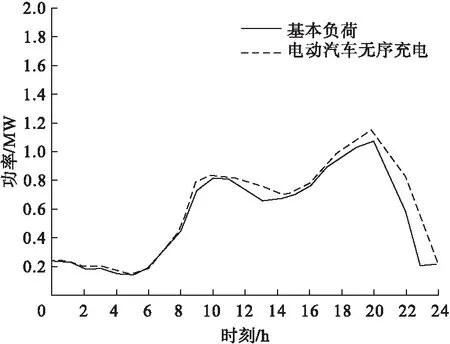
图5 含电动汽车充电需求的负荷曲线

由图5分析可知，当大规模电动汽车无序接入电网进行充电时，其充电需求将会使得大电网负荷峰上加峰，增加了电网的峰谷差，并影响了电网的稳定运行。结合图4光伏发电系统仅在6:00-18:00之间才会有出力，因此在微电网中光伏发电系统不出力或出力不足时，需要配备相应的储能维持系统的稳定运行，在光伏出力过剩的情况下吸收微电网中富余的功率进行储能。而图5中在17:00之后光伏出力不足，而电动汽车进行充电，导致微电网中负荷增加，配备的储能容量增加，不利于系统的经济运行。

假定粒子数目为80，分为四个粒子群，每个粒子群内含有20个粒子，最大迭代次数为100。在优化算法下对电动汽车充放电加以有序控制后的负荷曲线如图6所示。

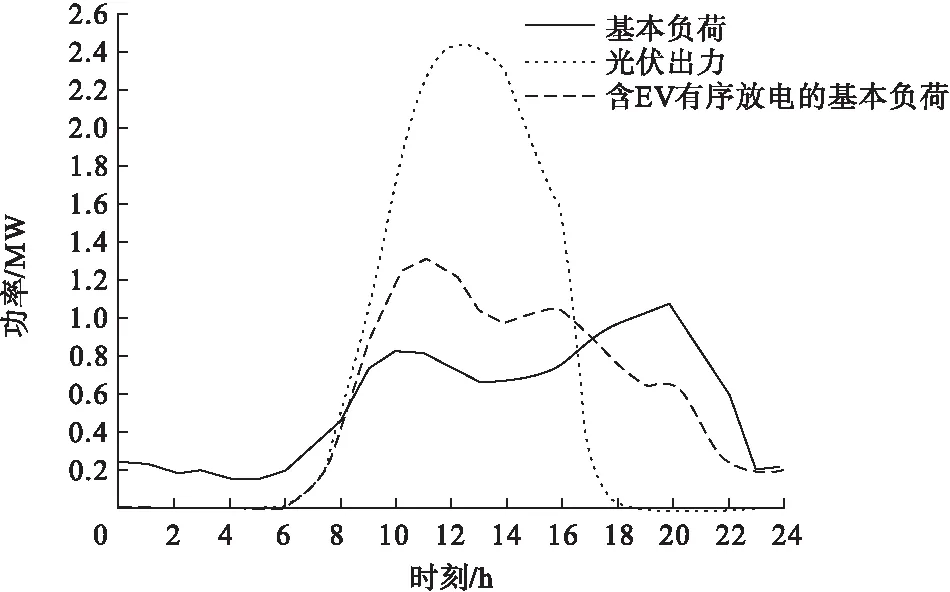
图6 含电动汽车有序充放电的负荷曲线

图6中电动汽车在光伏出力较大的情况下选择充电，储存能量；而在光伏出力不足或不出力的情况下选择放电，减小储能的出力，从而相应地减小储能的配置容量。通过对电动汽车充放电加以控制，发挥其分布式储能特性，使得负荷特性与光伏出力曲线更加匹配，提高光伏发电的利用率，降低储能配置的要求。仅含基本负荷、含EV无序充电、含EV有序充放电三种情况下的传统储能出力如图7所示。

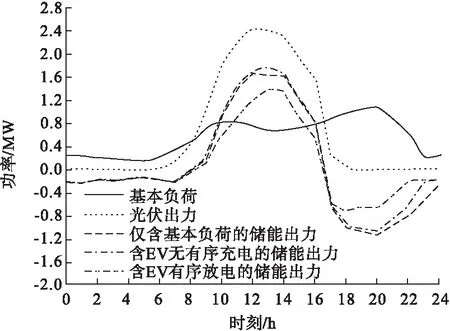
图7 三种情况下储能的出力

由图7分析可得，在含基本负荷的情况下，传统储能系统在16:30-8:00阶段处于放电阶段，以维持基本负荷的供电；而在8:00-16:30之间，光伏发电有所富余，利用传统储能进行储存富余的电能。将含EV无序充电的储能与含EV有序充放电的储能进行比较，含EV有序充放电的传统储能出力较少，储能的配置需求有所降低。通过有序的充放电控制，使得负荷从光伏发电不足或未出力的时段转移到了中午光伏发电富余的时段，改善负荷的特性，使之与光伏出力曲线匹配。

某站点电动汽车充放电控制策略，如表1所示。功率大于0则表示充电，功率小于0表示放电。两者之间的性能如表2所示，改进PSO算法的适应度值小于PSO算法，所以改进PSO算法的效果要优于PSO算法。

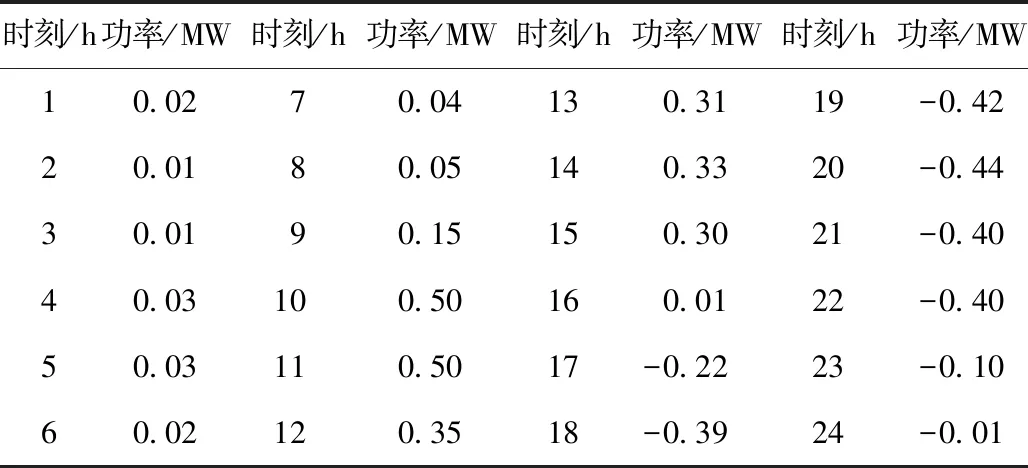
表1 电动汽车充放电策略

表2 两种算法性能比较

6 结论

本文以某区域内孤岛运行的小型微电网为研究对象，以总负荷需求与光伏发电功率之间差值的标准差最小为目标建立数学模型，利用改进粒子群算法对其求解。结果表明该算法可以实现电动汽车充放电功率的合理有序分配与规划，减小了总负荷需求与光伏出力之间的差值并保证微电网的稳定运行。同时，利用具有一定出行规律的EV分布式储能的作用，减少传统储能的出力，降低储能配置需求，提高微电网对光伏的消纳能力。通过比较两种算法，可得到改进粒子群算法克服了传统粒子群算法局部最优的缺陷，更有寻优效果。

文中仅考虑了含光-储的小型微电网，进行互动的EV规模相对还比较小，且在分析过程中并没有考虑电动汽车充放电过程电池性能变差、功率损耗等因素，未充分结合各种天气、环境和节假日的情景进行对比验证，在后续的研究中将予以考虑。