机器人用RV减速器曲柄轴弯曲应力分析

刘珂荧，吴鑫辉，冯长建，李文龙(. 大连工业大学 机械工程与自动化学院，辽宁 大连 6034；.大连民族大学 机电工程学院 智能感知与先进控制国家民委重点实验室，辽宁 大连 6605)

在RV减速器传动效率测试试验中，施加额定载荷，同向连续运转18个小时，当继续加载到额定负载的120% (1 040 N·m)，运转到第5分钟时，三个曲柄轴几乎同时断裂，试验过程中曲柄轴断裂的情况如图1。为了分析额定负载工况下曲柄轴弯曲应力，改进曲柄轴结构设计，本文采用理论计算和有限元分析分别计算曲柄轴弯曲应力。基于有限元法，建立RV减速器有限元装配模型，对曲柄轴弯曲应力进行有限元分析，有限元分析能够考虑到摆线轮变形、曲柄轴承滚子变形和曲柄轴变形对不同位置的曲柄轴受力的影响，使得曲柄轴弯曲应力分析更加接近工程实际。

图1 断裂的曲柄轴

1 曲柄轴弯曲强度理论计算

取RV减速器中任一曲柄轴及与其相固连的行星轮为研究对象，曲柄轴及行星轮的受力简图[1]如图2。

图2 曲柄轴及行星轮受力简图

根据曲柄轴及行星轮的受力简图列出关于x、y方向的力与力矩平衡方程：

∑Fx=0,

Fgr-FG1r-FG2r=0 ；

(1)

∑Fy=0,

Fgt+FA2+FD2-FG1t-FG2t=0 ；

(2)

∑Mx(F)=0,

FA2(a1+b+c)+FD2(a1+c)+FA1cos(θ-αc)(a1+b+c)-FD1cos(θ-αc)(a1+c)-FG1t(a1+a2+b+c)-FG2tc=0 ；

(3)

∑My(F)=0,

FG1r(a1+a2+b+c)+FG2rc+FA1sin(θ-αc)(a1+b+c)-FD1sin(θ-αc)(a1+c)=0 。

(4)

联立式(1)～(4)，求解得到曲柄轴支撑轴承的支反力FG1t、FG1r、FG2t和FG2r。

FGt={FA2(a1+b+c)+FD2(a1+c)-(Fgt+FA2+FD2)c+[FA1(a1+b+c)-FD1(a1+c)]cos(θ-αc)}/(a1+a2+b) ；

(5)

FG1r={[FA1(a1+b+c)-FD1(a1+c)]sin(θ-αc)-Fgrc}/(a1+a2+b) ；

(6)

FG2t=Fgt+FA2+FD2-FG1r；

(7)

FG2r=Fgr-FG1r。

(8)

通过求解得到曲柄轴旋转一周，曲柄轴支撑轴承的支撑反力的变化趋势如图3。

图3 曲柄轴支撑轴承支反力

根据试验过程中曲柄轴的断裂情况，选择研究的危险截面位置如图4中截面Ⅰ。

图4 危险截面示意图

危险截面Ⅰ处绕x轴弯矩

Mx=FG2t(a1+a2+b-28)+Fgt(a1+a2+b+c-28) 。

(9)

危险截面Ⅰ处绕y轴弯矩

My=FG2r(a1+a2+b-28)+Fgr(a1+a2+b+c-28) 。

(10)

危险截面Ⅰ处合成弯矩

(11)

通过计算得到曲柄轴旋转一周，危险截面Ⅰ处合成弯矩变化趋势如图5。

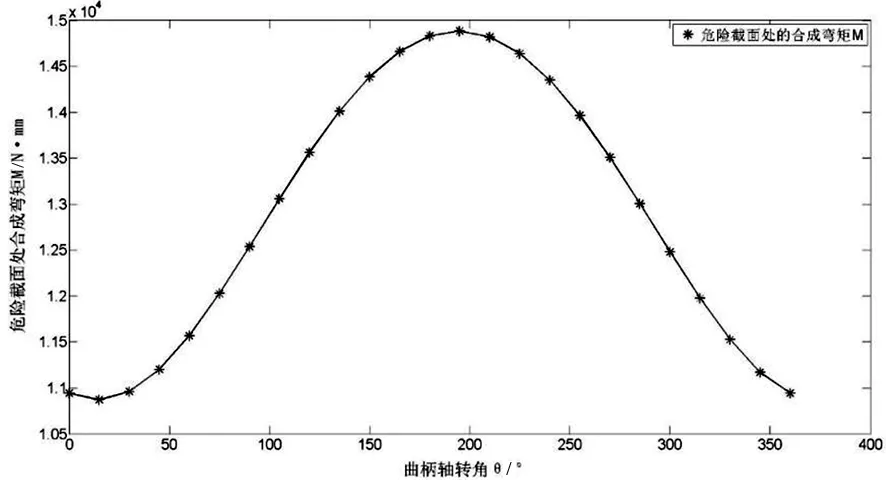
图5 危险截面Ⅰ处合成弯矩

Mmax=1.488 2×104N·mm 。

(12)

危险截面Ⅰ处绕z轴转矩

(13)

曲柄轴在工作过程中同时承受弯矩和转矩的作用，属于复杂应力状态，转矩按脉动循环变化计算，应用轴类零件弯扭校核公式

(14)

考虑应力集中的最大弯曲应力

σmax=ασ·σ=173.25 MPa 。

(15)

式中，应力集中系数ασ=3.5。

将异形刀片加工成形，安装到实际割草车上开展试验研究，验证其割草效果。虽刀片扭矩有一定下降，但刀口的切割速度依然很高，实际割草效果仍能达到要求。经试验测试结果表明，优化后刀片上的扭矩减小了18%左右，与仿真计算的误差小于5%，证明仿真结果有效。另外刀片功率减小了216 W，节能约8.5%，达到了满意的节能效果。图15(a)是试验用割草车,图15(b)是优化后的异形刀片。

2 曲柄轴弯曲应力有限元分析

RV传动是由渐开线行星传动与摆线针轮行星传动组成的一个完整的封闭式差动机构体系，如果只把曲柄轴从机构中单独取出来进行有限元计算，那么机构体系中几个重要计算对象之间的相互影响就很难准确地反映到计算模型中，计算结果也将失去一些精度。为避免上述缺陷，在计算模型中应将摆线轮、曲柄轴、曲柄轴承和行星轮同时引入计算[2-3]，这样才能使计算结果更加准确可靠。

2.1 计算方案确定

RV减速器中曲柄轴的自转将转速转矩输入第二级摆线针轮传动，同时曲柄轴将摆线轮自转产生的转速转矩输出，即在RV减速器中曲柄轴既受到转矩的作用，产生扭转变形，又受到两摆线轮沿曲柄轴承孔分布圆周切向力的作用，引起曲柄轴在此方向上的弯曲变形[4]。

RV减速器实际传动过程是一个多体接触问题，因为完整的计算模型接触部分太多，非线性计算收敛困难，因此将针齿和针齿壳简化，把啮合力直接作用在两个摆线轮的理论啮合点上，可以依据啮合位置的不同，对任意个齿面施加任意变化的啮合力进行计算。

2.2 RV减速器有限元装配模型建立

2.2.1 基本设计参数

RV减速器设计参数见表1，零件材料属性见表2。

表1 RV减速器设计参数

表2 零件材料属性

2.2.2 装配模型建立

机器人用RV减速器是高精密减速器，对建模精度要求很高，曲柄轴承的滚柱直径5 mm，宽度8 mm，14个滚柱均匀分布，轴承径向间隙取0.016 mm。3个行星轮用节圆代替与曲柄轴连接，装配模型如图6。

(a)A面视图 (b)B面视图

2.2.3 有限元网格划分

有限元网格的疏密影响计算结果的精度，考虑到两片摆线轮是主要传递载荷零件，摆线轮齿部分网格划分较密，可以真实地反映局部的应力与变形情况[5]。考虑到摆线轮上曲柄轴孔作为曲柄轴承的外圈，传递扭矩过程中，与轴承滚子接触传力，所以摆线轮上曲柄轴孔表面网格划分较密，曲柄轴与曲柄轴承滚子接触传力，因此曲柄轴表面网格细化，所有零件均采用六面体网格。

2.2.4 边界条件和载荷施加

根据摆线针轮传动受力分析理论[6]计算得出，同时啮合的齿数为9个，齿号为2-10号，受力结果见表3。

将摆线轮齿面啮合力分别作用在9个齿面上，在理论齿面啮合线上均匀分布。在行星轮的啮合节点处按啮合力方向进行约束，模拟太阳轮对行星轮的啮合力。曲柄轴两端圆锥滚子轴承按简支承处理。摆线轮上曲柄轴孔与曲柄轴承各滚子之间的接触，曲柄轴与曲柄轴承滚子之间的接触，均采用“面对面”的接触单元模拟它们的弹性接触[7-10]，RV减速器有限元装配模型如图7。

表3 摆线轮受力理论分析结果

(a)A面视图 (b)B面视图

2.3 有限元计算结果分析

规定图8中右上方的曲柄轴为1号曲柄轴，左上方的曲柄轴为2号曲柄轴，下方的曲柄轴为3号曲柄轴。

(1)当两片摆线轮的载荷相同时，曲柄轴最大应力分布如图8。

(a)1号偏心轴 (b)2号偏心轴 (c)3号偏心轴

1号曲柄轴的最大弯曲应力为162.377 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处；2号曲柄轴的最大弯曲应力为156.012 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处；3号曲柄轴的最大弯曲应力为176.468 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处。

(2)当输入端摆线轮的转矩为额定转矩的55%，而输出端摆线轮的转矩为额定转矩的45%时，偏心轴最大应力分布如图9。

(a)1号曲柄轴 (b)2号曲柄轴 (c)3号曲柄轴

1号曲柄轴的最大弯曲应力为148.073 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处；2号曲柄轴的最大弯曲应力为141.243 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处；3号曲柄轴的最大弯曲应力为188.14 MPa，最大应力的位置发生在曲柄轴与偏心凸轮的交汇处。

由上述分析可以看出，有限元分析结果与理论分析结果误差很小，在额定载荷工况下，3个曲柄轴的最大应力是不同的，在145～180 MPa之间，最大应力的位置都发生在曲柄轴与偏心凸轮的交汇处，说明曲柄轴应力集中明显，因为曲柄轴的结构是严格按照设计图纸尺寸建立的模型。

不同的摆线轮载荷分配情况下，计算得到的曲柄轴弯曲应力值不同，说明曲柄轴的弯曲应力状态对零部件加工误差和轴承间隙比较敏感。

3 结 论

(1)建立了考虑主要零部件之间的相互接触，行星轮、曲柄轴承、曲柄轴以及摆线轮变形的RV减速器有限元装配模型，利用该模型可以高效而准确地分析曲柄轴弯曲应力情况。

(2)RV减速器零部件加工误差和曲柄轴承间隙对曲柄轴的应力状态影响很大，在额定载荷工况下，3个曲柄轴的最大应力是不同的，最大应力的位置都发生在曲柄轴与偏心凸轮的交汇处，曲柄轴应力集中明显，应通过适当增大过渡圆角和优选热处理工艺以减小曲柄轴最大弯曲应力，提高曲柄轴弯曲强度。

参考文献：

[1] 李力行. 摆线针轮行星传动的齿形修正与受力分析[J]. 机械工程学报，1986(1)：18-23.

[2] 何卫东，吴鑫辉，卢琦. RV传动中摆线轮及曲柄轴承有限元分析[J]. 大连交通大学学报，2016(4)：67-71.

[3] 陈兵奎，谭磊，钟晖. 摆线包络行星传动接触有限元分析及系统开发[J]. 机械强度，2013,35(3)：366-371.

[4] 李力行，何卫东，王秀琦，等．机器人用高精度RV传动的研究[J]. 大连铁道学院学报，1999，20(2):1-3.

[5] 伍迪，张有忱. 基于ANSYS 的多齿差摆线齿轮有限元分析[J]. 机械设计，2009，26(5) : 40-41．

[6] 何卫东，李力行，徐永贤，等. 高精度RV传动的受力分析及传动效率[J]. 机械工程学报，1996(4)：104-110.

[7] 杨生华. 齿轮接触有限元分析[J]. 计算力学学报，2003，20(2)：189-194.

[8] 徐彬，陈南，王辉，等． 基于接触单元法的复杂机构有限元分析[J]．东南大学学报:自然科学版，2009，39(3) ：495-501．

[9] GUO Y, PARKER R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model. Mechanism and Machine Theory, 2012(51): 32-45.

[10] 吴鑫辉. 机器人用RV减速器齿形优化新方法及传动精度研究[D]. 大连：大连交通大学，2016.