某轨道试验车非线性有限元结构动力学分析

白 云，李舜酩

(南京航空航天大学 能源与动力学院， 南京 210016)

某轨道试验车是用于标定试验的特殊车辆，具有结构复杂、纵向尺寸大、运行速度高、可靠性要求高等特点。应某轨道专用车项目要求对该轨道试验车结构进行动力学分析。轨道试验车的牵引和制动过程是典型的复杂机械系统受力和运动过程,在运动过程中,试验车在不同的工作阶段表现出不同的动态特性。这种特定的动态特性对于轨道试验车的工作可靠性、运行稳定性都会产生十分重要的影响,是轨道试验车结构设计过程中必须考虑的主要因素。因此，为提某高轨道试验车的设计质量、缩短研制时间、减少投入，就需要在某轨道试验车的设计阶段对其动态特性进行有限元结构动力学分析。

非线性有限元[1]已逐步应用到结构动力学分析中，使得在复杂系统的结构动力学分析时更容易得到动力学响应结果。结构动力学的重要作用是分析和预测激励作用下系统的特性[2]。动力学分析一般包括两方面的内容：① 固有特性问题，包括系统的各阶固有频率、振型等；② 动态响应问题，包括系统的位移、速度、加速度等。本文应某轨道专用车项目要求对该轨道试验车进行非线性有限元结构动力学分析，利用ABAQUS/Standard的隐式动力学来模拟该轨道试验车的运动过程，获得整车的动态响应和车体的应力、变形以及关键部件应力云图，以验证整车设计的合理性。

1 结构动力学分析基础理论

在ABAQUS/Standard模块中使用Newton-Raphson算法来求解非线性方程。在进行非线性分析时，主要通过半增量步长残差进行方程迭代平衡控制。运用ABAQUS/Standard模块中的Newton-Raphson算法求解非线性问题[3-4]时是将增量和迭代组合起来，将受力体所受荷载分成若干个增量逐步施加给该受力体，然后在每个增量步内通过迭代的方法得到该问题的1个近似解，当该近似解偏离平衡位置时将进行下一次迭代，直到得到1个可以接受的解时该增量步才会结束，最后所有的增量步响应的总和就是问题的近似解答,具体求解过程如图1所示。图1中，曲线为荷载作用下结构的非线性反应；P为结构上的外力；U为位移；kto为结构初始刚度；kta为第1次迭代结束时计算得到的刚度；内力Ia、Ib；ΔP1、ΔP2为载荷增量；ΔU为位移增量。

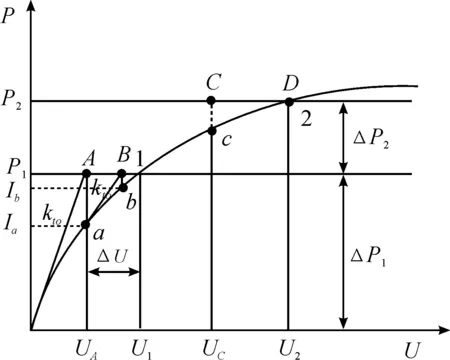
图1 Newton-Raphson迭代法求解过程

假定求解方程时第一次迭代计算的初始位移U=0，荷载产生一个小的增量ΔP1，求解其位移U1，记图1中初始切线刚度为kt0，则可通过式(1)[8]得到当前的位移增量ΔU:

kt0ΔU=ΔP1

(1)

根据位移增量ΔU即可得到此时的位移UA，它为结果U1的1个估计值，内力I和外力P的残差力RA为

RA=P1-Ia=P1-kUA

(2)

式中：k是基于当前位移构型UA估算出来的刚度矩阵；kUA是单元在当前状态下所提供的阻力(即内力)。可见此时内力与外力并没有达到平衡，必须进行下一步迭代，以使残差力RA减小到容许值以下。下一步迭代将从a点开始，沿着曲线a点的切线方向，得到一个更加精确的位移值UB，基于此位移值再进行求解，得到第2次迭代的残差力；若此残差力仍不小于容许值，就要进行第3次迭代，这样一直循环下去，直至小于容许值，达到平衡条件为止，就完成了1次荷载增量的计算。然后再采用此增量步中相同的迭代方法进入下一个荷载增量ΔP2的迭代计算，得到下一个增量步的最终解答，一步一步地计算下去，直至完成整个计算。

2 试验车的建模

2.1 设计要求

根据测试功能要求所设计的轨道试验车结构需要满足：

1) 车体要有足够的强度来装配其他总成。

2) 车辆最高运行速度为300 km/h，沿直线行驶。

3) 牵引最大正向(X方向)加速度为4.5g，加速度力的方向位于车辆纵向中间轴面内且与地面成斜向上35°夹角；制动最大加速度为2.3g，制动力沿水平方向(X方向)作用于车辆尾部两端。

4) 车体的离地间隙不能超过300 mm。

2.2 设计方案

某轨道试验车车体主要由3根纵梁和3根横梁以及中间带有圆孔的加强板焊接构成，全长6 m,最大宽度3.5 m,最大高度差0.6 m。对于车架具体设计方案如下：

1) 为满足高加速度运动时的强度要求、稳定性要求，主要结构采用箱型焊接梁，并在梁的内部对称布置一些加强板来提高强度。

2) 车体结构左右对称、合理分配载荷，并利用导向片沿导轨进行导向，以满足直线行驶要求。

3) 试验车整个设计要以较小的离地间隙为考虑重点。由于试验车负载较大、加速度过高，所以为保持稳定性，车辆重心不能太高。因此，采用直径为600 mm的车轮来满足离地间隙的要求。

最终设计方案如图2所示。牵引系统在牵引工况为整车提供牵引力，使轨道试验车能在短时间内达到最高运行速度；制动系统在制动工况为整车提供制动力，使轨道试验车能在短时间内停下来；轨道和导向片共同作用以保证轨道试验车沿直线行驶；防撞块装配在导向片上以防止其在行驶过程受到撞击。由图2中的几何模型也可以看出：轨道试验车车体结构对称，并且内部对称布置了带有圆孔的加强板，这样既节省了材料又提高了车体强度；车体重心低，离地间隙小。

图2 轨道试验车的几何模型

3 模型与仿真分析

3.1 建立有限元模型

本文中车体采用合金钢板冲压而成，大多属于薄板件，因此选用板壳单元对车体进行网格划分[5]，其他部件均划分成实体单元。利用有限元软件中的网格划分功能对某轨道试验车划分网格。考虑到试验车整体尺寸，网格划分时采用单元尺寸的大小为20 mm，对主要受力部位进行网格细化[6]。整个轨道试验车有限元模型由481 177个单元，862 336个节点组成，其中：166 586个壳单元，单元类型为S8R、S4R；314 591个实体单元，单元类型为C3D8I、C3D10M。整车有限元分析模型如图3所示。轨道试验车所用材料为42CrMo、Q345C，材料参数[7]如表1所示。

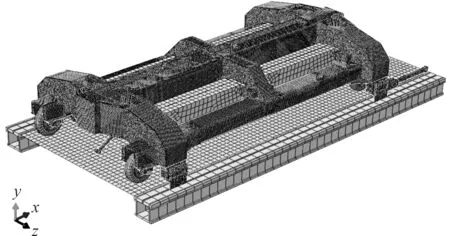
图3 轨道试验车有限元模型

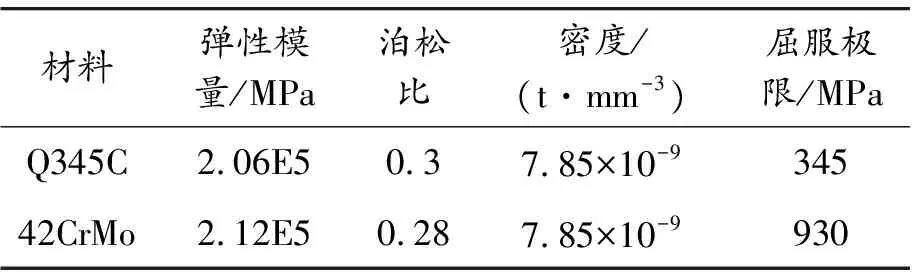
材料弹性模量/MPa泊松比密度/(t·mm-3)屈服极限/MPaQ345C2.06E50.37.85×10-934542CrMo2.12E50.287.85×10-9930

3.2 强度和刚度评估原则

材料不发生屈服破坏的条件为

(3)

式中:[σ]表示材料的许用应力;σ1、σ2、σ3分别表示X、Y、Z三个方向的主应力。车架在典型工况下的最大局部应力应满足：

(4)

式中:σs表示材料的屈服极限;n表示安全系数，一般取1.0～1.6，本研究取n=1.5。车体使用的材料为Q345C，σs= 345 MPa，许用应力为230 MPa；牵引系统和制动系统等关键部件使用的材料为42CrMo,σs=930 MPa，许用应力为620 MPa。

根据EN12663标准[8]，对车体刚度的主要要求是使车体结构1阶弯曲固有频率不低于10 Hz。1阶弯曲固有频率的理论计算公式为

(5)

由式(5)可以推导出车体挠度的理论计算公式为

(6)

式中：g为重力加速；wc为车体结构自身质量，wc=68 kN；w为垂向载荷，w=278 kN；fc为1阶弯曲固有频率；δ为车体挠度量。由fc≥ 10 Hz，结合式(6)可以得出某轨道试验车车体挠度量δ≤10.4 mm。

3.3 部件间连接的模拟

针对轨道试验车的实际运动关系，建立了不同的约束、连接关系。对整个系统建立了通用接触。

1) 约束定义

耦合约束[9-10](coupling)是在模型的某个区域和参考点之间建立约束。耦合约束有运动耦合(kinematic coupling)和分布耦合(distributing coupling)之分。本文有很多地方用到了运动耦合，这有利于施加边界条件和载荷，也容易施加连接单元(connector element)。在牵引杆头部中间设置1个参考点，并在此参考点与牵引杆头部两个圆柱面区域的各节点之间建立一种运动上的约束关系。图4为外载荷牵引力与牵引杆头部的运动耦合。

图4 运动耦合

2) 连接单元

连接单元用来模拟模型上2个点之间(或1个点和地面之间)的运动和力学关系，所连接的点称为“连接点”(connector point)。每个连接单元必须赋予1个连接属性，连接属性(connector property)的作用是描述连接单元2个连接点之间的相对运动约束关系。

本文中牵引系统以及制动系统等关键部件与车体之间通过螺栓连接，假设所用螺栓是高强度螺栓且不会断裂，因此用Beam连接单元来模拟螺栓连接，如图 5所示。此外，牵引系统牵引杆与牵引杆座、制动系统制动杆与制动座、车轮与车体之间的连接关系用Hinge连接单元来模拟，如图6所示。Beam连接单元约束了6个相对自由度，两点之间不允许发生相对平移和相对旋转。Hinge连接单元约束了5个相对自由度，两点之间不允许发生相对平移，只能沿着第1点的局部1方向发生相对旋转。

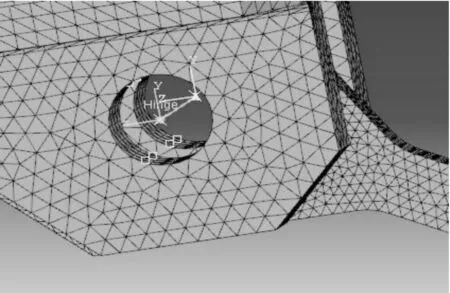
图6 Hinge 连接单元

3.4 边界条件与载荷

1) 牵引工况

模拟某轨道试验车由外在牵引装置通过牵引系统在一定时间内达到300 km/h。外在牵引装置提供的牵引力Fqy以集中力的形式直接施加在牵引杆头部(沿牵引杆方向)，牵引力Fqy随时间t变化的关系曲线如图7所示。此工况下的边界条件为：6个车轮的位置施加Y向约束；牵引系统-牵引杆头部约束X、Y、Z方向的旋转自由度；两侧防撞块施加Z向约束；为了使模型更容易收敛，同时不影响计算结果的精确度，对4个导向片与导轨接触部位施加临时Z向约束；导轨施加6个自由度的完全约束。

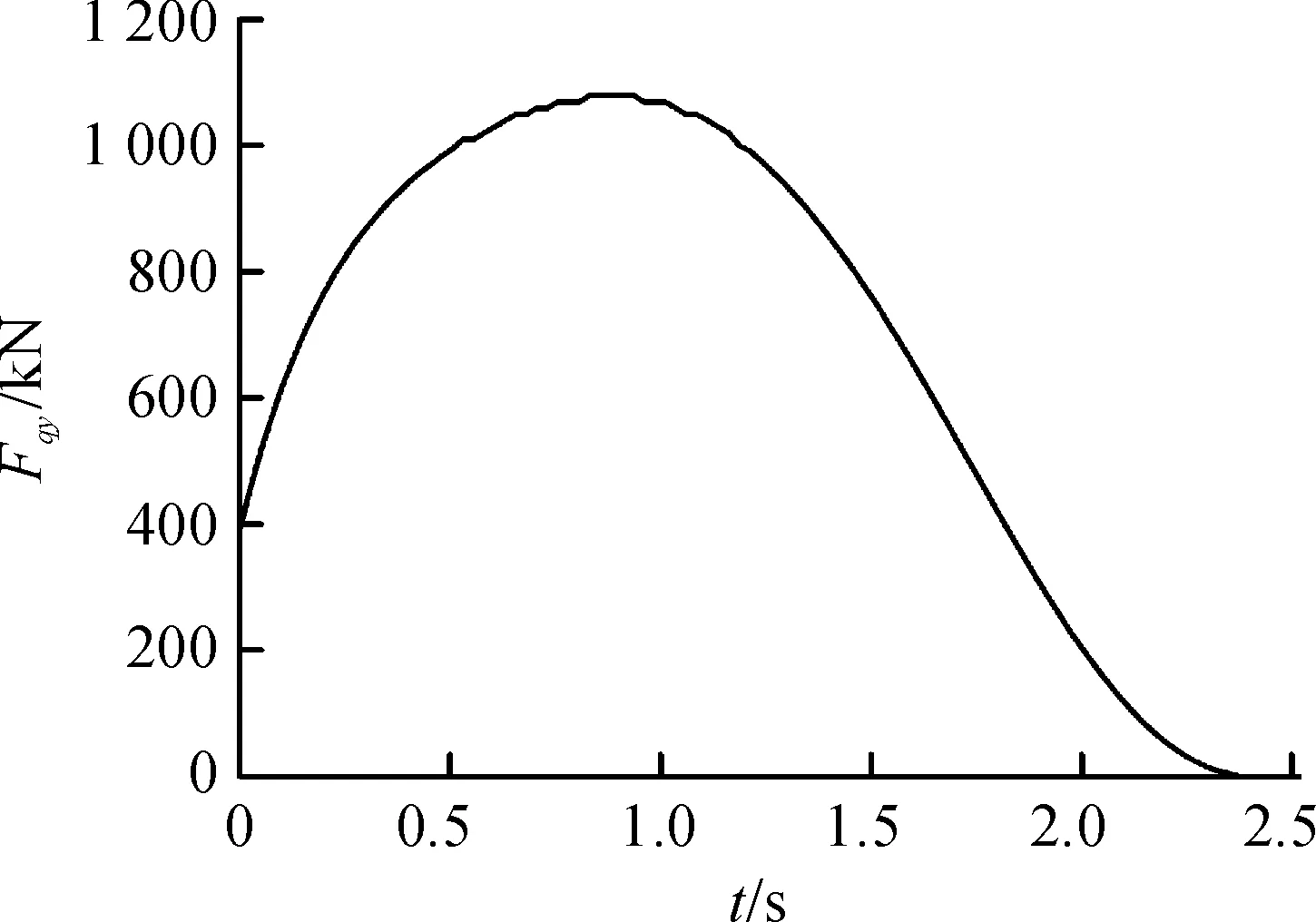
图7 牵引力曲线

2) 制动工况

模拟某轨道试验车通过制动系统在一定时间内速度由300 km/h降为0。制动力(方向沿X轴正向)直接施加在制动系统相关位置，制动力Fzd随时间t变化的关系曲线如图8所示。此工况下的边界条件为：6个车轮的位置施加Y向约束；两侧防撞块施加Z向约束；对制动系统-制动杆约束X、Y、Z方向的旋转自由度；与牵引工况一样对4个导向片施加临时Z向约束；导轨施加6个自由度的完全约束。

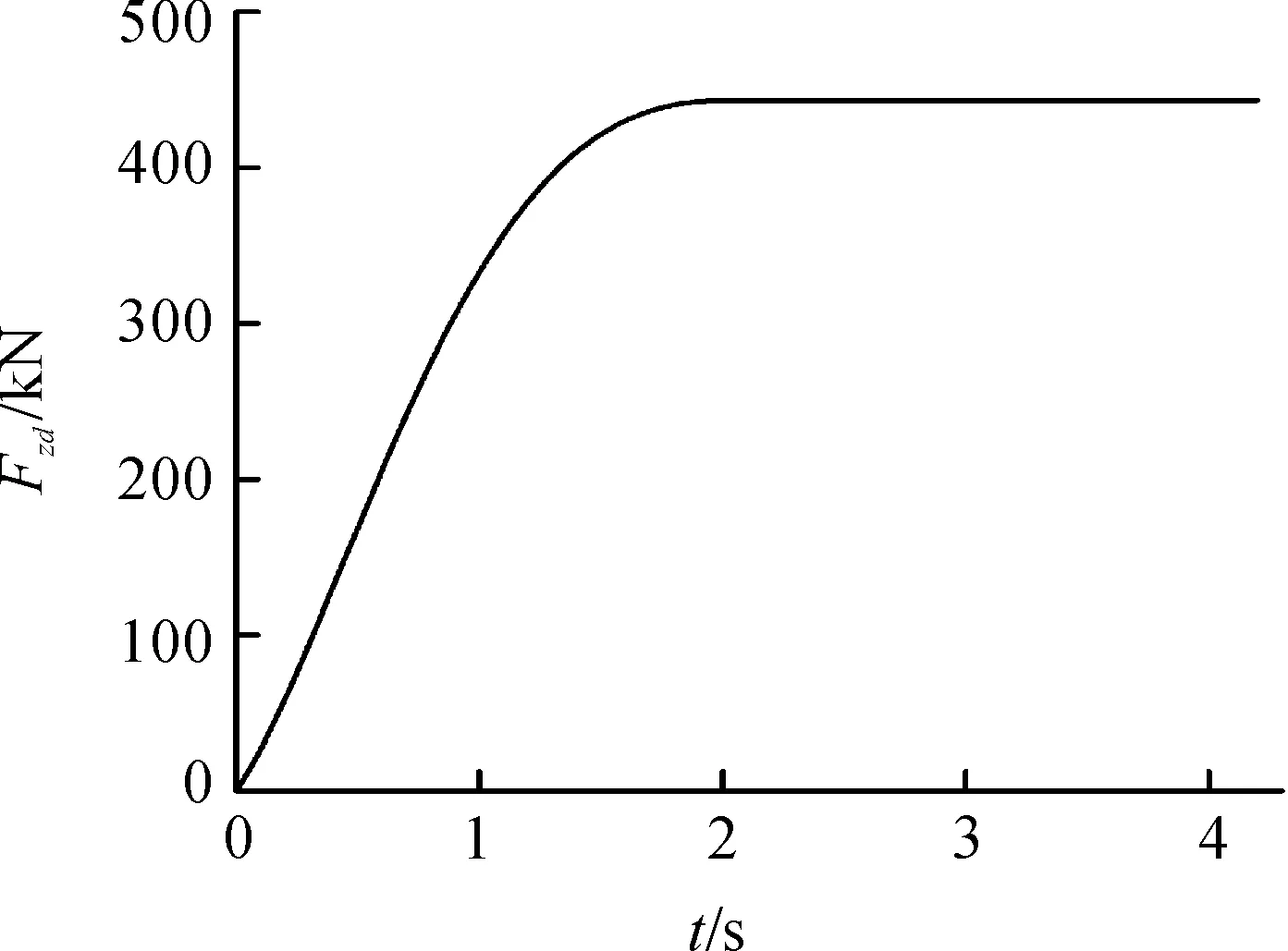
图8 制动力曲线

4 有限元分析结果

应用前面介绍的ABAQUS/Standard隐式动力学求解方法计算获得了某轨道试验车在2种工况下结构的动态响应。

4.1 牵引工况下的结构响应

通过对某轨道试验车在牵引工况下的隐式动力学分析，获得了整车在此工况下的加速度、速度、位移变化曲线，以及车体的应力、变形和关键部件的应力云图。

图9～11为轨道试验车在牵引工况下的加速度、速度、位移曲线。由轨道试验车X方向加速度Aqy随时间t变化的关系曲线(图9)可以看出：轨道试验车整车的加速度Aqy(X方向)在0～0.93 s内极速增大，在0.93 s达到最大45.12 m/s2，之后随着时间延长而缓慢减小。由图9和图7可以看出：加速度Aqy和牵引力Fqy的曲线形状基本一致。由轨道试验车X方向速度Vqy随时间t变化的关系曲线(图10)可以看出：轨道试验车整车的速度Vqy(X方向)先随时间延长而极速增大，在1 s之后随着时间延长而缓慢增大，整车在2.3 s的速度Vqy达到最大值83.37 m/s。图9～11反映了整车牵引工况下的运动规律，同时可以看出加速度Aqy达到了4.5g、速度Vqy达到了300 km/h，符合设计要求，进而说明牵引工况下的载荷及边界条件的施加较为合理。

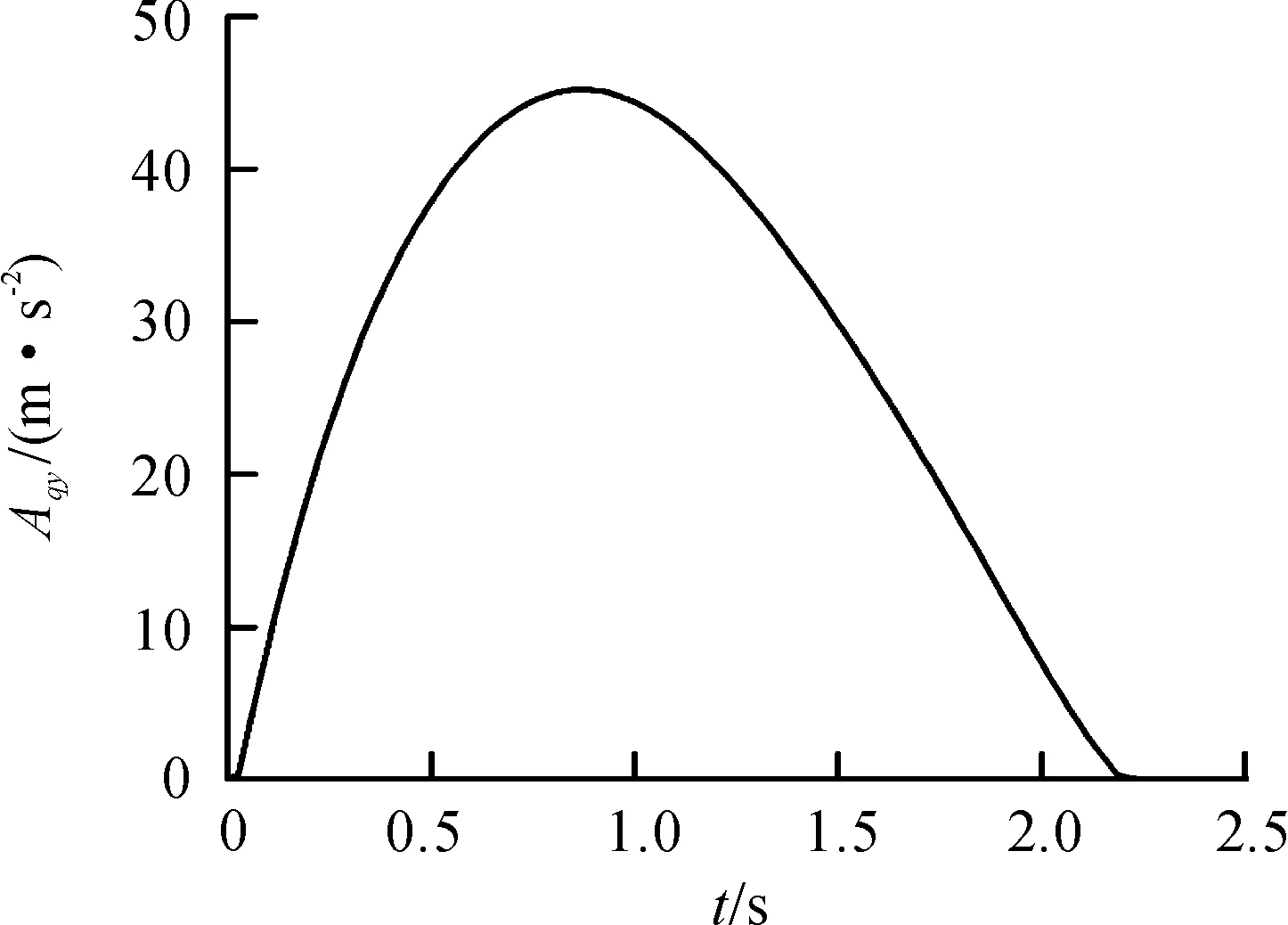
图9 轨道试验车X方向加速度曲线

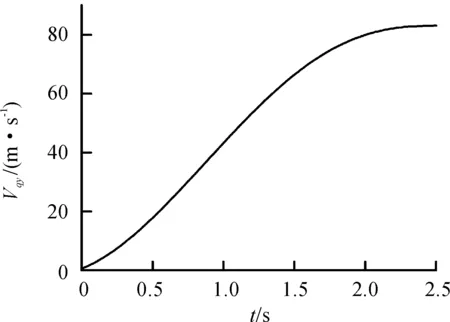
图10 轨道试验车X方向速度曲线

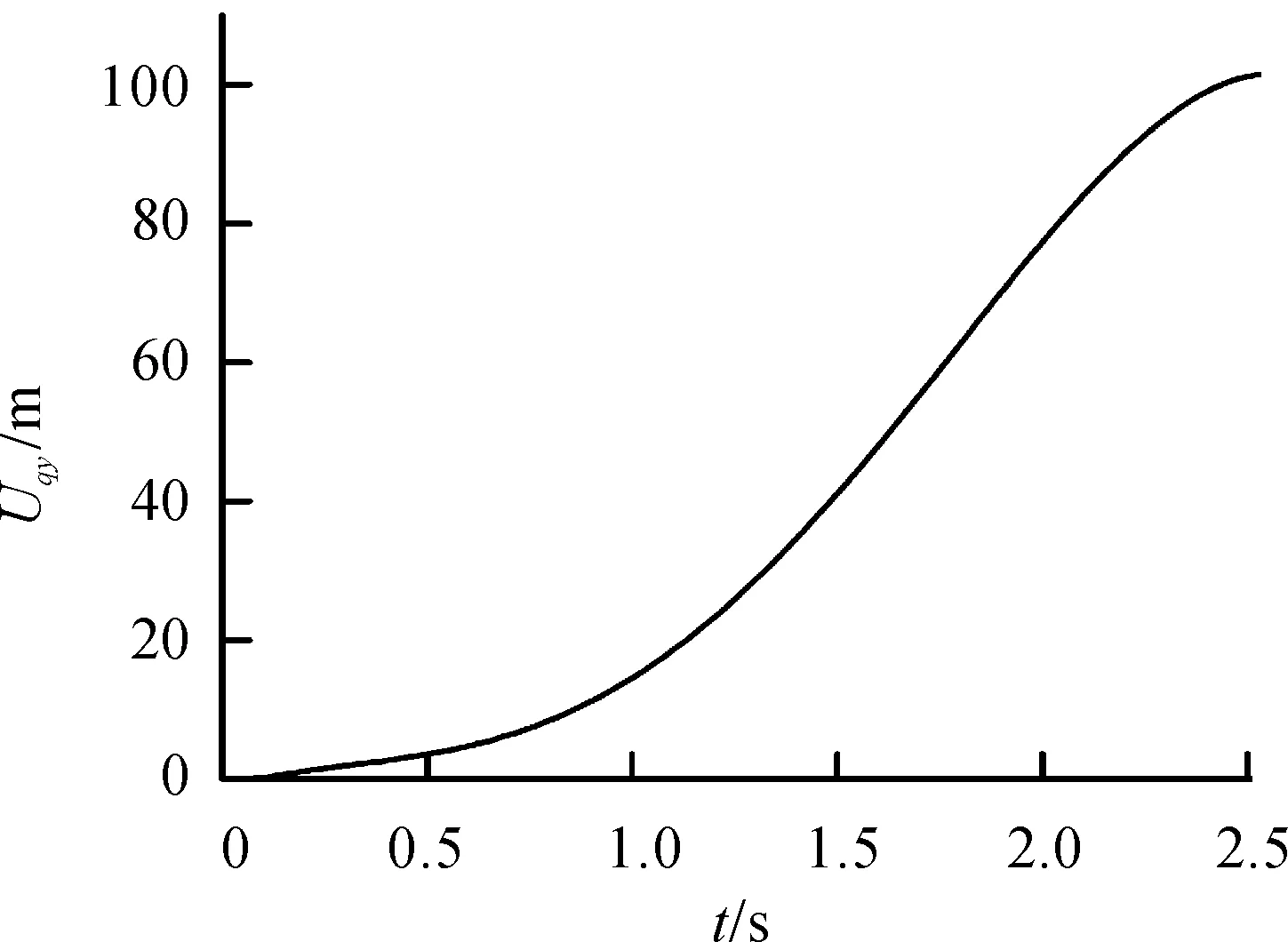
图11 轨道试验车X方向位移曲线

图12～15为轨道试验车在牵引工况下的应力和变形云图。由图12～13可以看出：牵引工况下车架最大应力为191.6 MPa(小于许用应力230 MPa)，发生在车架第1根横梁与中间纵梁焊接处，与牵引杆座连接处应力也相对较大；此工况下车架的变形最大为2.359 mm(小于10.4 mm)，发生在与牵引杆座连接处。

由图14可以看出：牵引系统-牵引杆座的最大应力为264.7 MPa(小于许用应力620 MPa)，发生在与车架连接处。由图15可以看出：牵引系统-牵引杆头部在圆角处出现了严重的应力集中，在圆角附近的应力值非常大，达到了723.1 MPa，其最大应力值虽然小于牵引杆材料的屈服强度930 MPa，但大于许用应力620 MPa，不能满足强度要求，必须改进结构来降低其应力值。

以上可以说明牵引工况下车体的应力和变形、牵引系统-牵引杆座的应力均满足设计要求，但牵引系统-牵引杆还需要进行结构优化来降低其应力值。

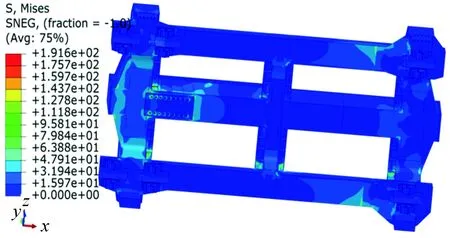
图12 车架应力云图

图13 车架变形云图

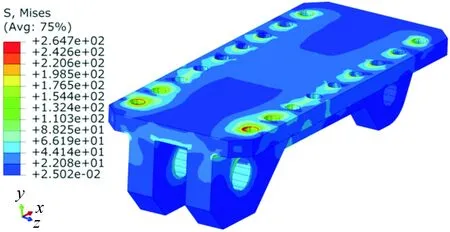
图14 牵引系统-牵引杆座应力云图

4.2 制动工况下的结构响应

通过对某轨道试验车在制动工况下的隐式动力学分析，获得了整车在此工况下的加速度、速度、位移变化曲线，以及车体的应力、变形和关键部件的应力云图。

图16～18为轨道试验车在制动工况下的加速度、速度、位移曲线。由轨道试验车X方向加速度Azd随时间t变化的关系曲线(图16)可以看出：在加速度Azd的开始阶段，曲线有轻微的波动，这是因为在两侧制动力的作用下，车辆被拉回中轴线X方向运行(加速阶段Z向存在3 mm位移)；随着时间t的延长，加速度Azd平稳增大，在2.41 s加速度Azd达到最大值23.3 m/s2；之后保持不变直到轨道试验车停止。由轨道试验车X方向加速度Vzd随时间t变化的关系曲线(图17)可以看出：由于在制动开始阶段，车辆在两侧制动力作用下被拉回中轴线X方向直线行驶，因此在0～0.5 s左右的时间段内速度Vzd并没有减小；之后随着时间的延长，速度Vzd由83.37 m/s先缓慢减小然后再快速减小，在4.3 s左右速度降为0，轨道试验车停止。图16～18反映了整车制动工况下的运动规律，由此运动规律可以看出，制动加速度Azd达到了2.3g，符合设计要求，同时说明制动工况下施加的载荷以及边界条件较为合理。

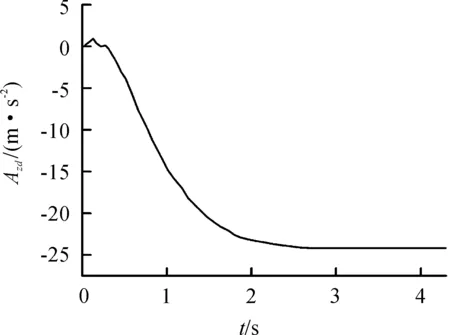
图16 轨道试验车X方向加速度曲线

图19～22为轨道试验车在制动工况下的应力和变形云图。由图19、20可以看出：制动工况下车架最大应力为210.1 MPa(小于许用应力230 MPa)，发生在两侧纵梁与第3根横梁焊接处，因为此处的钢板与6根箱梁的焊接钢板相比较薄，中间横梁与两侧纵梁焊接处应力也相对较大；此工况下车架的变形最大为1.649 mm (小于10.4 mm)，发生在制动系统-制动座连接处，同时车架两侧纵梁接近尾部(在2、3根横梁之间)的变形也相对较大。

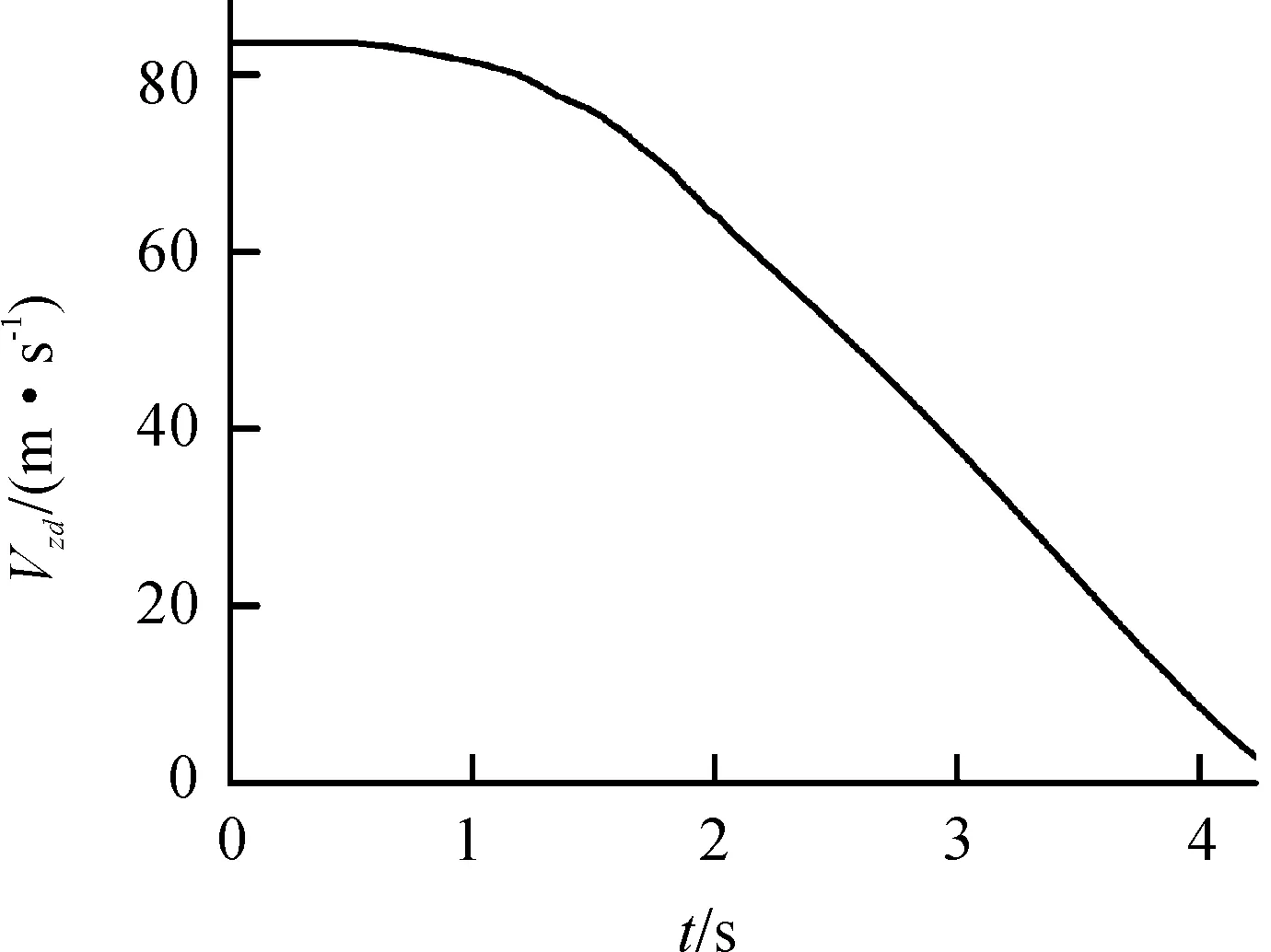
图17 轨道试验车X方向速度曲线

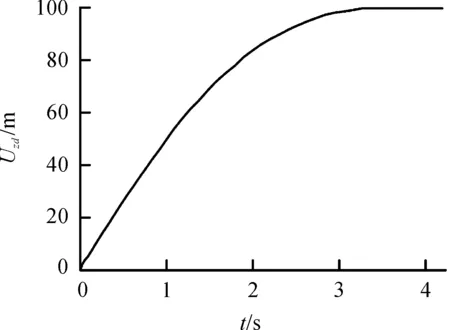
图18 轨道试验车X方向位移曲线

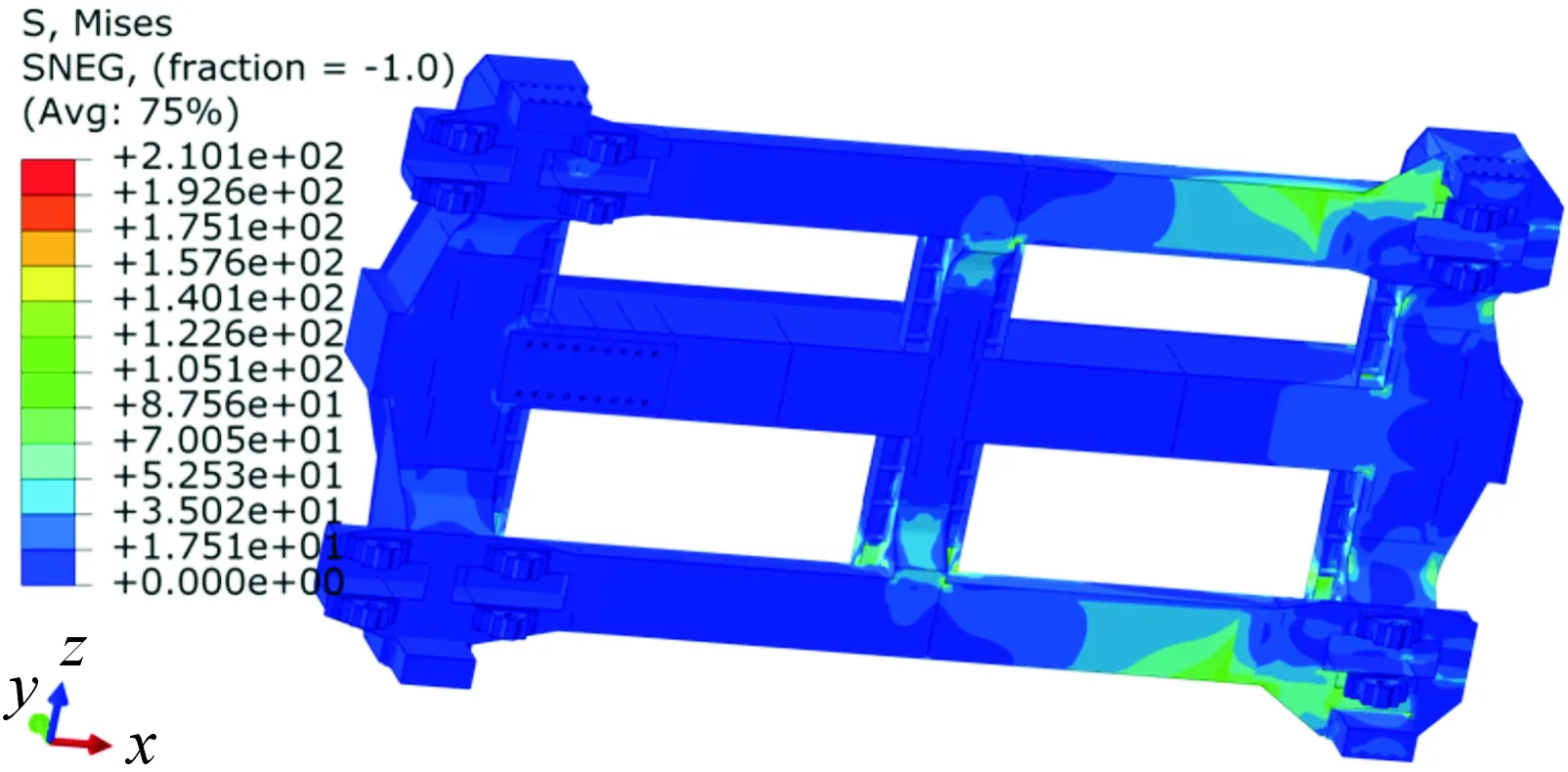
图19 车架应力云图

图21 制动系统-制动座应力云图

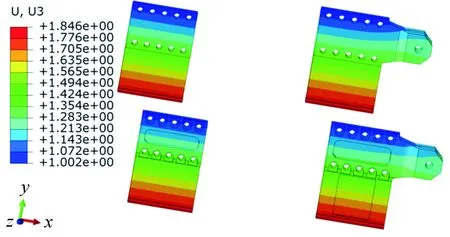
图22 导向片Z向变形云图

由图21可以看出：在制动工况下，制动系统-制动座的最大应力为301.9 MPa(小于许用应力620 M Pa)，发生在与制动杆销轴连接孔处。由图22可以看出：4个导向片在Z向(U3)变形最大为1.846 mm，发生在导向片与导轨接触的部位，而导向片初始离导轨有3 mm的间隙，进而说明轨道试验车沿轨道直线行驶。

以上可以说明，制动工况下车体的应力和变形以及制动系统-制动座的应力均满足设计要求。

5 结论

1) 运用ABAQUS/Standard模拟某轨道试验车在牵引和制动工况的响应是非常有效的，从获得的加速度、速度及位移响应可以得到整车的运动规律。由运动规律可以得出：牵引工况下最大加速度和速度分别达到了4.5g和300 km/h；制动工况下最大加速度达到了2.3g，该轨道试验车在规定的时间内速度降为0，进而验证了整车结构设计是满足要求的。

2) 两种工况下车体的最大应力分别为191.6 MPa和210.1 MPa，均小于许用应力230 MPa，满足强度要求。两种工况下车体的最大变形量分别为2.359 mm和1.649 mm，均小于10.4 mm，满足刚度要求。牵引杆座以及制动座的最大应力分别为264.7 MPa和301.9 MPa，均小于许用应力620 MPa，满足强度要求。牵引杆的最大应力为723.1 MPa，小于材料的屈服极限930 MPa，但大于许用应力620 MPa，因此需要对牵引杆结构进行优化来降低其应力值。

[1] CRISFIELD M A.Nonlinear finite element analysis of solids and structures[J].Wiley,2012,119(7):16/1-16/6.

[2] 赵经文，王宏钮．结构有限元分析[M]．北京：科学出版社，2004.

[3] COOK R D.有限元分析的概念和应用[M].北京:科学出版社,1981.

[4] 徐跃良.数值分析[M].成都：西南交通大学出版社,2005.

[5] 曾发林,李德华,范嫦娥.某车架有限元建模及仿真研究[J].制造业自动化,2012,34(3):103-106.

[6] 明显诚,朱才朝,冉险生.全地形车车架的静态性能分析与结构改进[J].重庆理工大学学报(自然科学),2010,24(2):11-15.

[7] 黄武全,符旭,吴明苏，等.汽车材料[M].北京:机械工业出版社,2011.

[8] BEUTH V G H.EN12663-1/2010， Structurl requirements of railway vehicle bodies[S].Berlin:CNE,2010:13-17.

[9] 庄茁.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.

[10] 石亦平,周玉蓉．ABAQUS 有限元分析实例详解[M].北京:机械工业出版社，2006.