基于GPS定位系统的巡线员所巡电缆确定方法
刘 均, 张 怡, 刘 炯, 陆轶祺, 解 大
(1. 国家电网上海市电力公司 市北供电公司,上海 200072;2. 上海交通大学 电气工程系,上海 200240)
0 引言
随着电力系统规模的不断扩大,人们对其安全性、稳定性、可靠性等方面的要求也在不断地提高。然而,再精准的保护措施也无法确保电缆的稳定运行,总是会发生监测范围外的一些人为或自然因素,对电缆产生一定程度的危害,并进一步引发停电等事故。常见的有道路施工误挖电缆、车辆撞击、风筝或鸟兽造成短路等[1,2]。为了避免这一类事故的发生,需要定期地对输配电线路进行巡检,也就是开展定期的巡线工作。通过巡线往往能提前发现输配电线路中的隐患,并提前将其解决,降低事故的发生率。因此,在目前的电力系统中,巡线仍旧是不可或缺的一个环节[3,4]。
自20世纪90年代起,GIS地理信息系统逐渐开始在我国的电力领域中崭露头角。基于GIS的电力巡检技术对地理信息的描述是采用一个图形引擎与对属性文件进行管理,集合可视化与综合性于一体,可以很好地整合企业资源和客户关系的优势,因此在国外电力行业中已经有了较为广泛的应用[5]。GIS系统能够真实反映输电线路的实际位置走向以及沿线设备的地理位置等各种信息,巡视人员与管理人员通过调用视化系统能够了解线路状况,及时处理线路及设备故障。基于GIS的电力巡线系统使得输电线路信息更直观形象、有利于管理人员对线路的运行管理[6]。
通过调用巡线员携带的智能巡线设备中GPS模块,便能实时获取巡线员在工作中所处的具体位置[7]。本文基于定位所得的经纬度坐标及其转换方式,提出了一种巡线员与电缆位置匹配的算法。首先,通过巡线员的初始位置,将其与预期所巡电缆相匹配。然后对其工作中的位置进行监测,判断其是否偏离巡线路径[8]。最后,在巡线完成后依据坐标点列拟合其路径并计算误差。通过该算法可以实时监测巡线员工作状态并准确评估巡线工作的完成程度及巡线员工作情况。
1 巡线员巡线初始位置与电缆的匹配
限制巡线技术发展的一个重要因素就是巡线员具体巡线位置的确定。在提高巡线效率,辅助巡线员工作之前,如何保证巡线员巡检完毕系统所指定的那条电缆,是所有巡线管理系统所要解决的首要问题。随着通信行业的迅猛发展,卫星导航技术逐渐成为各国竞相发展的重点,而其中最为突出的就是美国GPS系统。该系统对于用户接收机的精准定位,解决了巡线位置的确定问题。在对巡线图划分的增强型网格基础之上,巡线员在工作时携带的智能巡线装置将会每5~10 s上传一次巡线员所处位置的经纬度坐标至巡线管理系统[9]。系统将会依据巡线员的前进方向自动将巡线员匹配到最近的一条电缆段上,视为巡线员正在巡检这一条电缆段。每次巡检完一条电缆段后,系统还将计算巡线员工作效率等数据,进行后期的分析处理工作。由智能巡线装置提供的巡线员具体坐标,将先判断该坐标所处的网格。确定了巡线员所处网格后,便需要进行类似于汽车导航的路径及电缆段的匹配工作。
Map matching功能是导航中必不可少的一项功能,它不需要定位达到非常高的精确度就能实现用户接收机位置与当前行驶道路的匹配[10]。这点对于巡线管理系统也是一样,因为巡线员在巡检时势必会沿着一条电缆径直前进而不会有很大的偏移。巡线员位置判断与车载导航的区别就是巡线员在没有巡检时可能在网格内的任意位置移动。
对巡线员实时位置的具体匹配过程如下:当巡线员要开始巡检一条电缆段时,由于电缆交汇或分差,系统将会自动为其匹配最近的某条或多条电缆段。巡线员实时位置匹配示意图如图1所示。
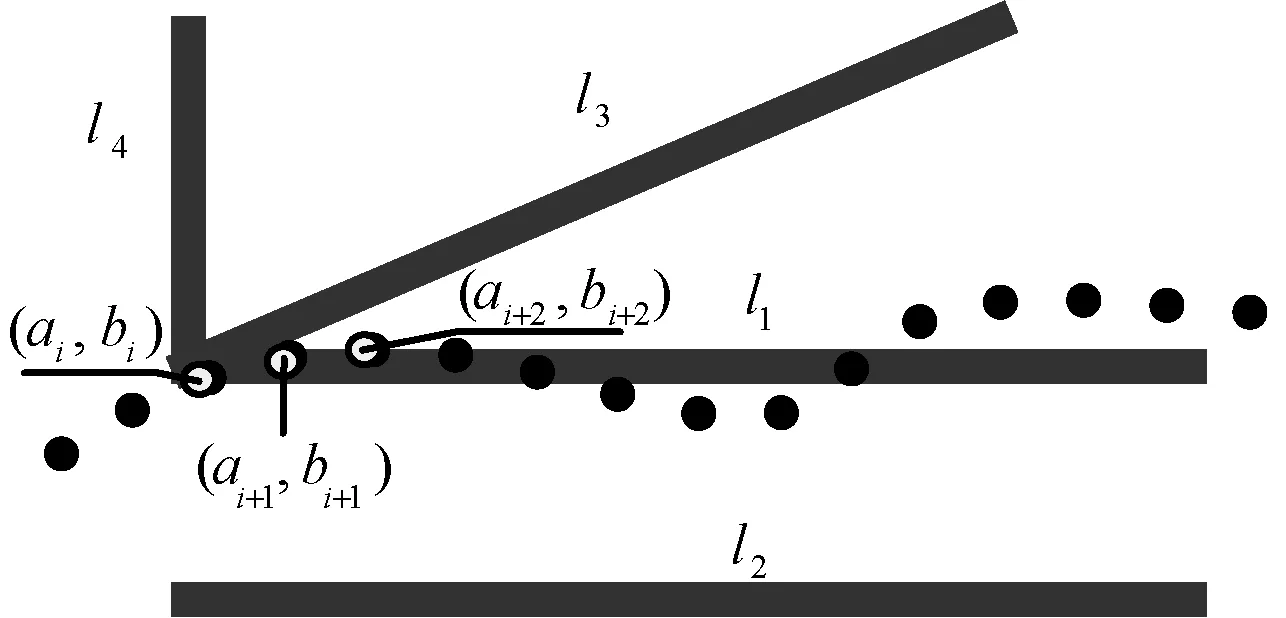
图1 巡线员与电缆段初始位置匹配示意图
记lj所在直线方程为b-klja-clj=0,巡线员实时位置的坐标为(ai,bi),此处的坐标为平面的城市坐标,可与经纬度坐标相互转换[11]。将网格内所有的电缆段置入备选电缆段集合L,再运用点到直线距离公式计算该初始位置与L内各条可能电缆段的距离dij:
(1)
由此便能选择可能的电缆段,若其间距离满足:
0≤dij≤1.5dsup
(2)
式中:dsup为系统认为巡线员在巡查这条电缆段时,其与电缆段之间可能的最大距离。用这些电缆段替换备选电缆段集合L。当L中只有一个元素时,该电缆段即为巡线员所巡查的线段。当L中包含多个元素时,先暂时以与巡线员距离最小的电缆段作为最大可能在巡电缆段。然后等待智能巡线装置之后5~10 s再次上传其坐标。
当巡线管理系统获取新的巡线员GPS坐标(ai+1,bi+1)后,便对L内所有电缆段再次计算巡线员与电缆段的距离:
(3)
同样进行比较:
0≤di+1,j≤1.5dsup
(4)
在此基础上还需将第一次的距离计算结果再次纳入考虑范围:
(5)
计算完成后,用符合条件的电缆段再次替换L中的所有元素,若L中元素多于1个,则再次等待巡线员下一次上传的坐标数据,并重复上述如(ai+1,bi+1)求解过程的步骤,此时的判断条件变为:
(6)
实际上,对于巡线员所巡电缆段的确定往往不会超过20 s,也即3点的巡线员路径坐标即可确定巡线员所巡的电缆段。
2 巡线员实时位置与电缆的匹配
巡线员位置与电缆段匹配完成之后,巡线员可能由于各种原因向其他方向运动,这时巡线员可以选择通过智能巡线装置暂停巡线工作,那么巡线管理系统则会将其工作时间暂停,并停止对其的监控,直至巡线员再度手动开启巡线工作。若巡线员并没有选择暂停,巡线管理系统则能判断出该巡线员终止了对该条电缆段的巡线工作。
巡线管理系统在巡线员巡查某一电缆段的任意时刻,均会利用式(1)计算巡线员所处位置与其所巡电缆段的垂直距离,如图2所示,一旦该距离超出了允许范围,也即:
dij≥dsup
(7)
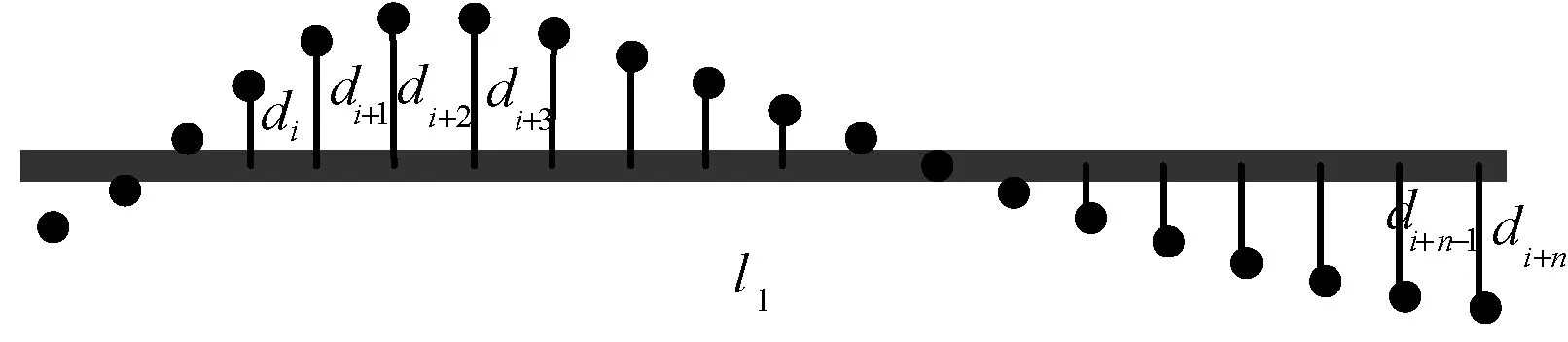
图2 巡线员与电缆段实时位置匹配示意图
则系统判定巡线员不再继续巡查该电缆段。当巡线员完成一条电缆段的巡检任务后,他便能通过智能巡检装置上传该电缆段的巡检信息,并通过巡线管理系统统一分析管理。
巡线员实时位置与电缆段的匹配工作是一种对于巡线员工作实时的数据处理方式,除此以外,巡线员上传的数据均将存储于数据库中。同时,巡线员在巡检每一条电缆段(l1)时,所上传的经纬度坐标(a1,b1),(a2,b2),(a3,b3),…,(an,bn)均会保存于该电缆段的集合L1中,而该集合则包含于网格集合G中。
3 巡线路径拟合及误差分析
巡线员巡线路径的拟合以及误差分析均是基于最小二乘法的原理实现的。在工程技术和科学实验中,常常得到两个有函数关系观测量的一系列有序对,如何根据这些有序对来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。为了解决这一类问题,最小二乘法应运而生,其基本思想是:给定一组实验数据,这些数据往往是有序数对,根据误差平方和最小化原则,找出这些数据的最佳函数匹配[12]。在利用最小二乘法实现曲线拟合时,虽然能够很好地拟合有序对,但是需要进行大量复杂的计算,而且得到的拟合函数往往是高次的,这进一步增加了复杂性。
将最小二乘法运用在巡线员的坐标位置变化上,便能大致拟合出巡线员所选择的巡线路径。在确保误差很小的前提下,为了有效利用巡线图增强型网格的特点,对于巡线员的最短路径拟合采取分段线性拟合的方式。巡线员每巡检一条电缆段,便视为一条拟合路径。因此,可以将该分段线性拟合的方式分为电缆段路径及非电缆段路径2类。
3.1 电缆段路径拟合
对于某一条选定的电缆段(l1),从其集合L1中调出其中的所有巡线员坐标元素(a1,b1),(a2,b2),(a3,b3)…(an,bn),对其的线性拟合将以电缆段l1所在直线方程b-kl1a-cl1=0为参照。设待求拟合直线为:
b-kl1a-cl1+Δcm=0
(8)
由于巡线员在巡检某电缆段时,其位置与该电缆段的相对位置偏差不会很大,因此直线方程(8)中唯一的待求量Δcm也会很小。使用最小二乘法的原理,选定一个足够小的循环步长ε,以及范围(mmin,mmax)内的整数循环步数m。这样一来,所要求的变量就成为了循环步数m。据此,便可以将拟合直线方程改写为:
b-kl1a-cl1+mε=0
(9)
计算(a1,b1),(a2,b2),(a3,b3),…,(an,bn)与其的距离平方均根,也即为巡线员路径相对于电缆段的误差值,根据式(1)可求得每点与电缆段的距离d11,d21,d31,…,dn1,并据此求得误差值:
(10)
对范围(mmin,mmax)内的整数m进行遍历,计算其Em的值,然后比较这些Em,其中最小的那个值对应的m0即为所要求的参数。
(11)
将其回代入式(9),便能得到通过最小二乘法所求得的电缆段路径拟合直线:
b-kl1a-cl1+m0ε=0
(12)
m的上限mmax和下限mmin分别是直线l1两侧距离其最远的两坐标点决定,若这两条直线分别为:
b-kl1a-cl1+Δcm1=0
(13)
以及:
b-kl1a-cl1+Δcm2=0
(14)
则易得mmax与mmin分别为:
(15)
(16)
巡线员在巡线时经过绝大多数均为电缆段路径,因此采取的近似电缆段所在直线的线性拟合算法将大大节省普通最小二乘法的计算复杂度,而其误差也并不会有太大的增加,这是巡线图增强型网格的一大优势。
3.2 非电缆段路径拟合
网格中的电缆段并不一定是全部邻接的,如图3所示的巡线员实时位置坐标集合、系统拟合路径以及电缆段之间将产生部分误差,巡线员也将势必在某两条电缆段的端点间自由移动。巡线员在这些位置移动时的坐标将被记录在L的补集CUL中,对于选定的某两条电缆段间的自由移动区域,不是一般性地同样以(a1,b1),(a2,b2),(a3,b3),…,(an,bn)来表示它们,通过一般的最小二乘法来拟合非电缆段路径。
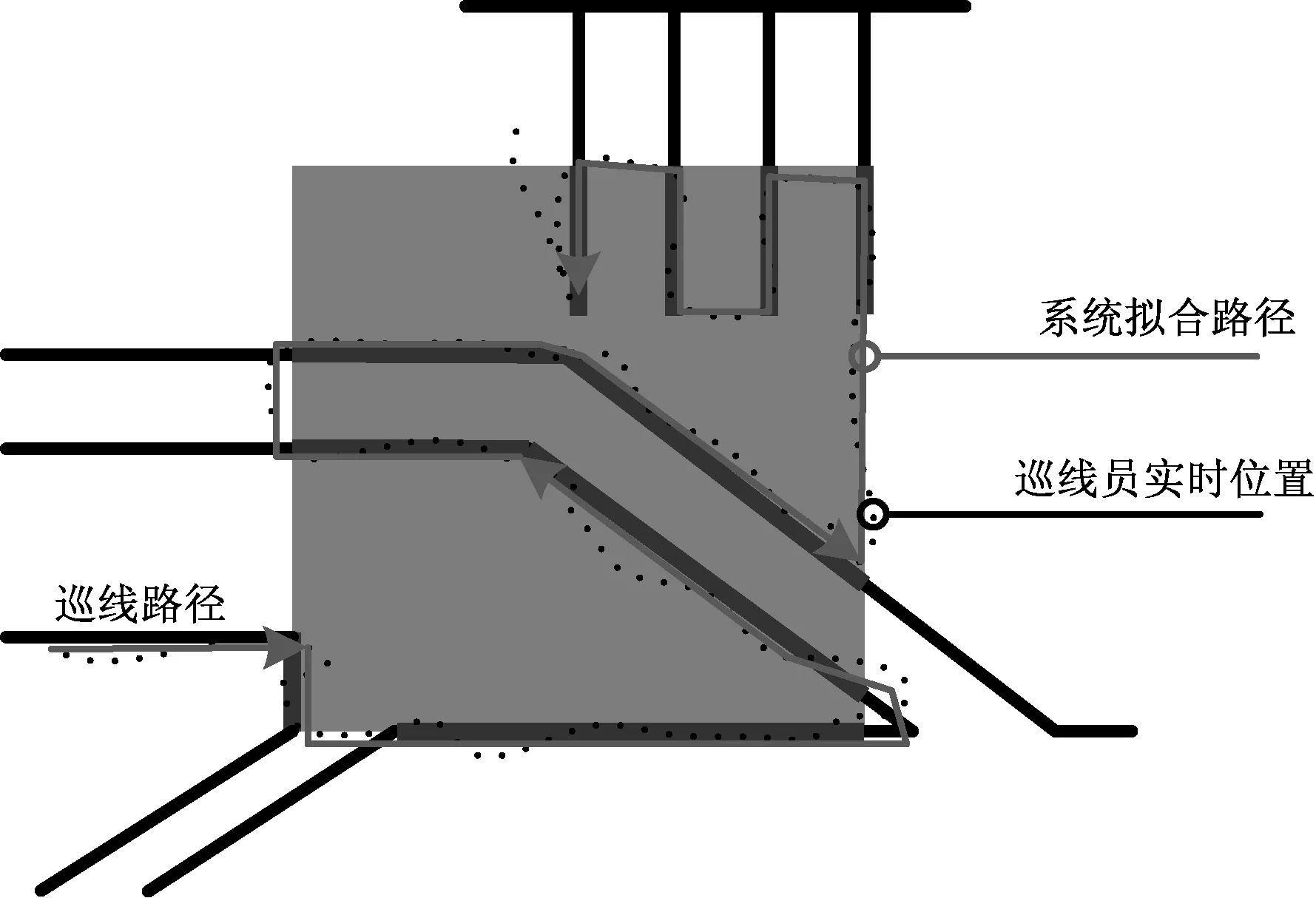
图3 模拟巡线路径拟合图
设所求拟合直线方程为
b-ka-c=0
(17)
待估参数为k及c,令
k=k0+Δk
(18)
c=c0+Δc
(19)
式中:k0及c0为k及c的初始值,一般选为巡线员之前或之后巡查电缆段的k及c值。
据此,便可以得到误差方程为:
(20)
将所有n个点的坐标代入,便能得到向量:
(21)
依据最小二乘法判别准则:
VTV=min
(22)
对应于VTV的最小值,便能得到所要求的k值及c值。
非电缆段路径在巡线管理系统中处于相对次要的地位,因为实际上只需要记录巡线员不在巡线时所消耗的时间即可。
3.3 误差分析
误差分析同样是针对巡线员在巡检电缆段时的路径而言的,对于某一选定的电缆段l1而言,巡线员所经过的坐标点为(a1,b1),(a2,b2),(a3,b3),…,(an,bn),则定义其巡线过程中的绝对误差为:
(23)
其相对误差为:
(24)
不难发现,e*的求解公式与式(10)相似。此类相对误差的提出是为了避免由于巡线员在不同电缆段巡线所花时间不同而造成的绝对误差差距。此相对误差在计算巡线效率及权重时有很重要的作用。
巡线员所携带的智能巡线装置也存在着定位精度的问题,因此在巡线员所处位置与电缆段匹配后的巡线过程中,系统认为巡线员在巡查这条电缆段时,其与电缆段之间可能的最大距离dsup一般定为5~10米,也即纬度经度相差0.1 s左右的距离偏差。
4 算例分析
为了检测巡线员与电缆匹配算法的实际效果,上海市市北块区域的电缆被选为试点区域,并安排进行实地测试。由于电缆段十分复杂,所以展示测试的一部分结果如图4所示,图中的黑点即为实验时所获取的巡线坐标点。巡线员携带着带有GPS定位功能的巡线设备正常工作,后台软件便能获取其实时坐标并记录下来与事先完成的电缆段拟合线段相比较,执行匹配算法,便能成功实现路径的匹配以及拟合。可以看出,在电缆段本身长度较短的情况下,由于获取坐标点的数量很少,因此对路径的匹配可能出现偏差。但由于其本身路径就短,所以实际效果并没有出现很大的误差。
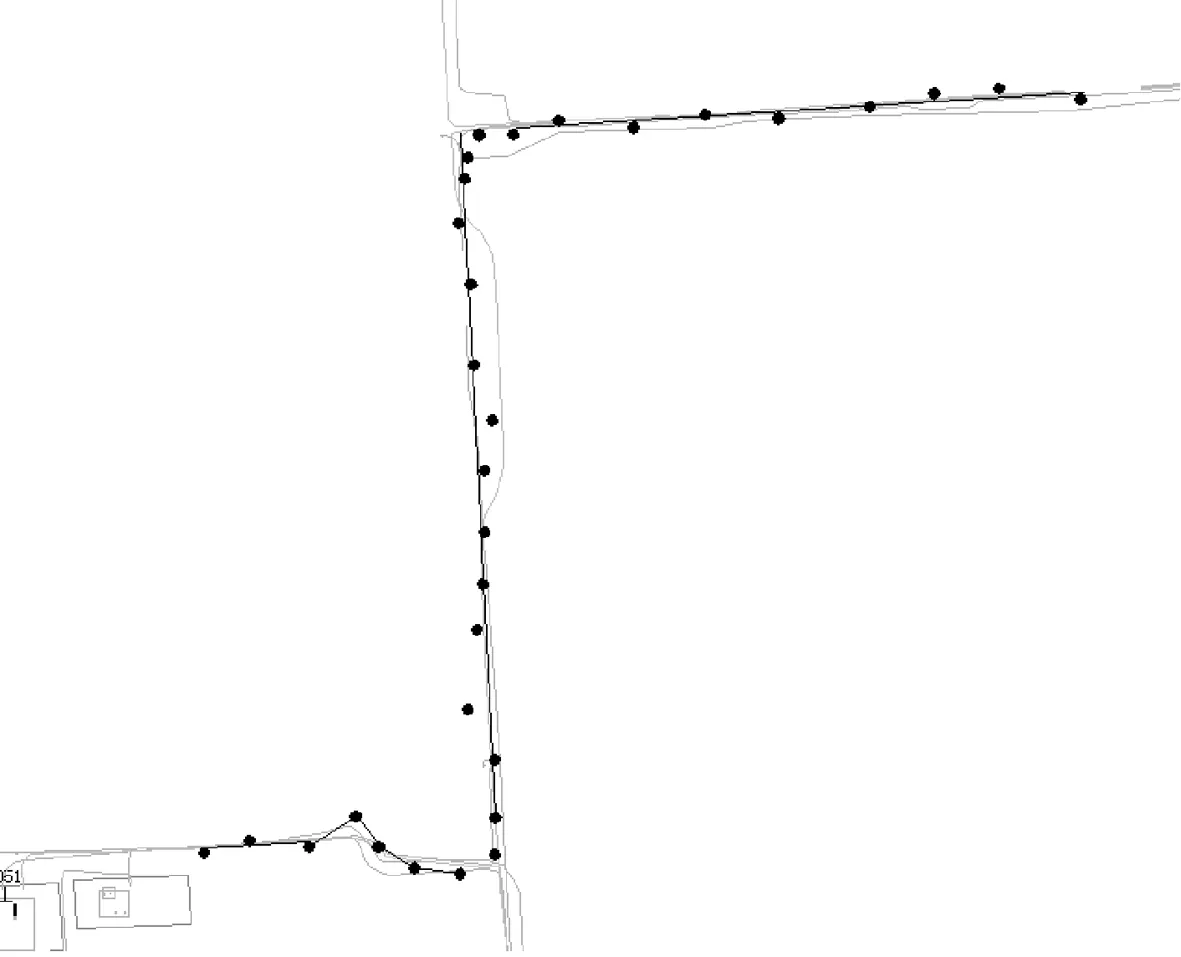
图4 模拟巡线路径拟合图
试验区域的某条路径取点情况如表1所示,该段路径自己电缆段近似直线方程为0.051 814x-y+338.988 65=0,而实际拟合直线方程为0.074 2x-y+493.494 7=0,两者在相同的区间[-6 925.289 6,-6 854.837 9]内偏差距离最大处仅1.05365。由于巡线员的配合,坐标偏差均质只有0.842。
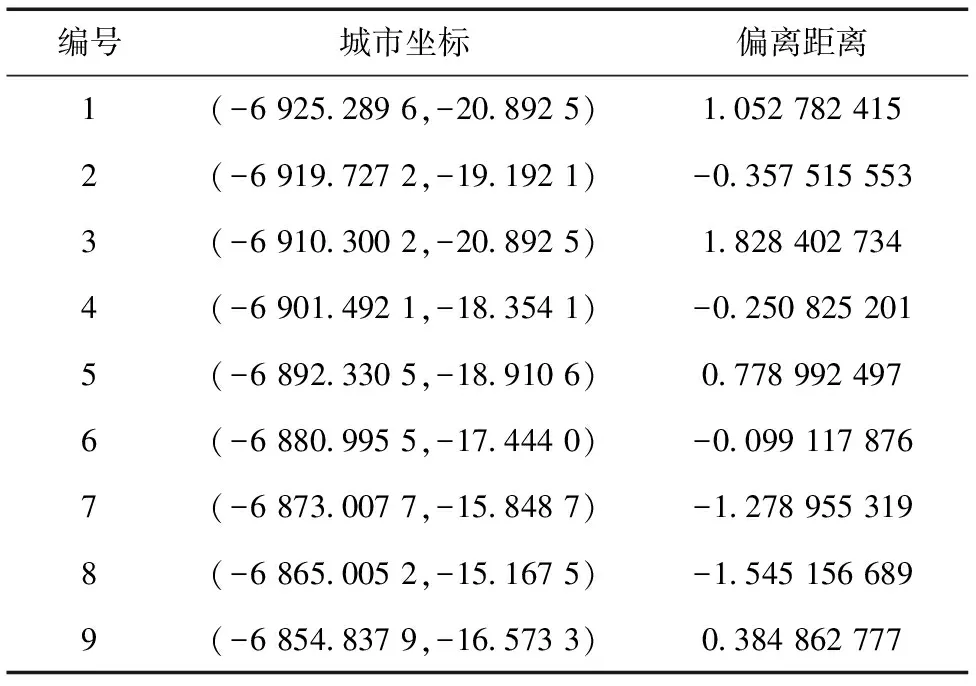
表1 单条路径数据表
在这次测试中,结果符合预期,主要的误差并不来源于路径匹配及拟合算法,而是来自电缆段向直线的近似。
5 结论
(1)提出了巡线员坐标散点与电缆段路径的匹配算法,能够有效地确定巡线工作时巡线员所巡路径,当电缆段路径较短时可根据需求手动改变坐标获取速率或允许偏差,实现具体目标。
(2)通过匹配算法得出属于同一路径的点列,并依据最小二乘法实现对于巡线路径的拟合及误差分析,从而为巡线工作的考核提供数据参照。
(3)具体巡线工作实践中,能够实现需求,与巡线管理软件及智能巡线设备契合度高,总体完成度也较高。
参考文献:
[1] 胡毅, 刘凯, 吴田,等. 输电线路运行安全影响因素分析及防治措施[J]. 高电压技术, 2014, 40(11):3491-3499.
[2] 蔡泽祥, 王星华, 任晓娜. 复杂网络理论及其在电力系统中的应用研究综述[J]. 电网技术, 2012, 36(11):114-121.
[3] 许金凯, 张立中, 金珈成,等. 高寒区机载电力巡线光电稳定吊舱系统设计及应用[J]. 中国电机工程学报, 2012, 32(31):200-208.
[4] 王鹏, 刘锋, 梅生伟,等. 高压输电线巡线机器人控制体系构建及动作控制器设计[J]. 清华大学学报(自然科学版), 2011,51(7):921-927.
[5] 闾国年, 袁林旺, 俞肇元. GIS技术发展与社会化的困境与挑战[J]. 地球信息科学学报, 2013, 15(4):483-490.
[6] 宋小冬, 钮心毅. 城市规划中GIS应用历程与趋势——中美差异及展望[J]. 城市规划, 2010,34 (10):23-29.
[7] 田雪竹, 初永良, 范永存,等. 基于农村电网的GPS巡线系统管理软件的设计[J]. 东北农业大学学报, 2009, 40(2):111-113.
[8] 韩小涛, 张哲. 基于智能手持机的高压巡线管理系统开发[J]. 电力自动化设备, 2003, 23(4):47-48.
[9] 陈得民, 张元. 基于网格划分的传感器网络定位方法的研究[J]. 计算机应用研究, 2009, 26(5):1685-1686.
[10] TONG X H, CHUN W U, QING W U, et al. A novel vehicle navigation map matching algorithm based on fuzzy logic and its application[J]. Journal of Central South University of Technology, 2005, 12(2):214-219.
[11] 谢鸣宇, 姚宜斌. 三维空间与二维空间七参数转换参数求解新方法[J]. 大地测量与地球动力学, 2008, 28(2):104-109.
[12] 田垅, 刘宗田. 最小二乘法分段直线拟合[J]. 计算机科学, 2012, 39(s1):482-484.

