PMSM带前馈控制的模型参考自适应矢量控制系统的研究
周 阳, 马立新, 袁沧虎
(上海理工大学 光电信息与计算机工程学院,上海 200093)
0 引言
因永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)拥有价格低廉、速度调节的范围宽以及动态响应快等优势,应用前景很广。在传统的磁极定向控制系统中,PMSM的精确控制基本依赖于准确的转子速度以及转子位置的测量,然而安装位置传感器,如光电编码器和旋转变压器,会使控制系统成本、体积增加,在某些场合受限,如温度较高的场所,限制了PMSM的应用推广[1~2]。无位置传感器控制为解决该问题提出了很好的方法。PMSM的无位置传感器技术无需安装位置传感器,利用检测到的电机绕组中的有关电信号,以及再利用一定的控制算法,从而对转速以及转子位置进行计算。
因此,越来越多的研究人员开始专注于无位置传感器控制系统的研究。目前已有许多控制方法可以对电机的转速进行估计,主要有基于基波数学模型的三相永磁同步电机无传感器控制和基于高频信号注入的三相永磁同步电机无传感器控制这两大类。其中基于基波数学模型的三相PMSM五传感器控制技术依赖三相PMSM基波激励数学模型中与转速有关的量(如产生的反电动势)进行转子位置和速度估算,由于电动机在零速和极低速时,有用的信噪比很低,通常难以提取。从根本上说,对基波激励的依赖性最终导致了相关方法在零速和极低速运行时对转子位置和速度的检测失效。因此,基于基波数学模型的三相PMSM无传感器控制技术主要应用于中高速场合,常用的控制算法有:滑模观测器算法(SMO)、模型参考自适应算法(MRAS)、扩展卡尔曼滤波算法(EKF)等[3,4]。
本文首先阐述了PMSM带有前馈控制的模型参考自适应矢量控制系统的原理,再设计合理的自适应律来对电机参数进行识别,再结合电压前馈解耦的控制方法,然后采用MATLAB建立系统的仿真模型,以此来验证该方法[5]。
1 算法原理
1.1 模型参考自适应算法原理
MRAS算法是一种自适应控制系统的算法。从结构上分MRAS算法可以分为可调模型、参考模型和自适应律3部分。MRAS的基本理论是:期望模型选取为不包含待定系数的表达式,可调节的模型选取为包含待定系数的表达式,此外,两个模型输出量要有一样的物理含义,然后再利用它们输出量的差值,利用选定适宜的自适应律对PMSM未知系数进行识别[6]。
1.1.1 参考模型与可调模型的确定
对于表贴式三相PMSM,同步旋转坐标系下的电压方程表达式[7~9]:
(1)
为了获得可调模型,对上式作变换,可得:
(2)
定义
(3)
则式(2)变为
(4)
再将(4)改写为状态空间形式:
(5)
其中:
从公式(5)可以得出,状态矩阵A中包含了转子转速,因此可以将该式当作可调模型,ωe为有待确定的可调系数,而三相PMSM的本体就选作参考模型。
1.1.2 参考自适应律的确定
将上式(4)用估计值形式来表示,可得[10]:
(6)
可简写为:
(7)

(8)
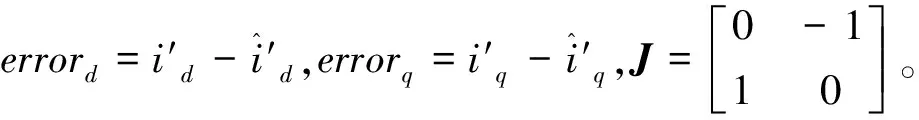
将公式(8)简写成以下形式:
(9)
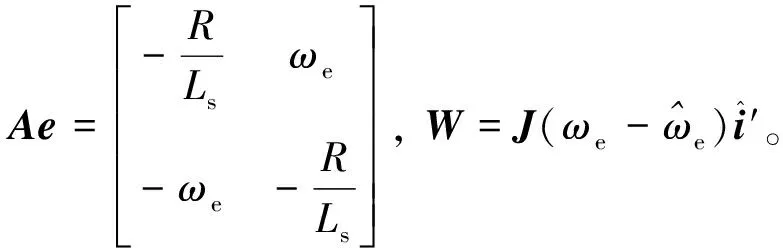
根据Popov超稳定理论,若想要让该控制系统处于稳定状态,得满足以下2个要求[11]:
1)传递矩阵H(s)=(sI-Ae)-1为严格正定矩阵;
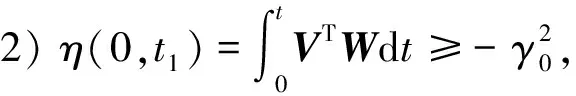

对Popov不等式进行反向计算可得所需的自适应律,且结果:
(10)
将式(10)改写为如下表达式:
(11)

将公式(3)代入公式(10),可得:
(12)
对公式(11)求积分,便可求得所需的转子的位置估算值:
(13)
MRAS的实现框图如图1所示。
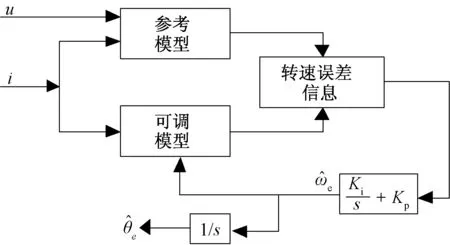
图1 MRAS的实现框图
1.2 电压前馈控制
由公式(1)定子电流id、iq分别在q轴和d轴方向产生交叉耦合电动势。
若id、iq完全解耦,式(1)变为[12~15]:
(14)
式中:ud0和uq0分别为电流解耦后的d轴和q轴电压。
将式(14)拉普拉斯变换后,可得
Y(s)=G(s)U(s)
(15)

利用常规的PI控制器并结合电压前馈解耦控制方法,可得到d-q轴电压分量为:
(16)
式中:Kpd和Kpq为PI调节器比例增益,Kid和Kiq为PI调节器积分增益。
电压前馈解耦单元的电流环PI控制器的系统结构框图,如图2所示。
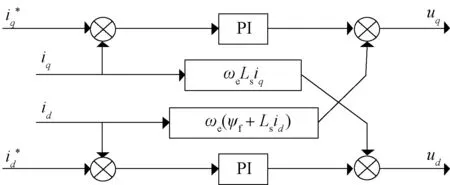
图2 前馈解耦单元系统结构方框图
2 MATLAB仿真验证及结果分析
根据图1所示的MRAS实现框图,采用MATLAB/SIMULINK构建系统仿真模型。MRAS的MATLAB仿真模型如图3所示。带有前馈解耦控制单元的MRAS三相PMSM无传感器矢量控制系统结构框图,如图4所示。

图3 MRAS仿真模型
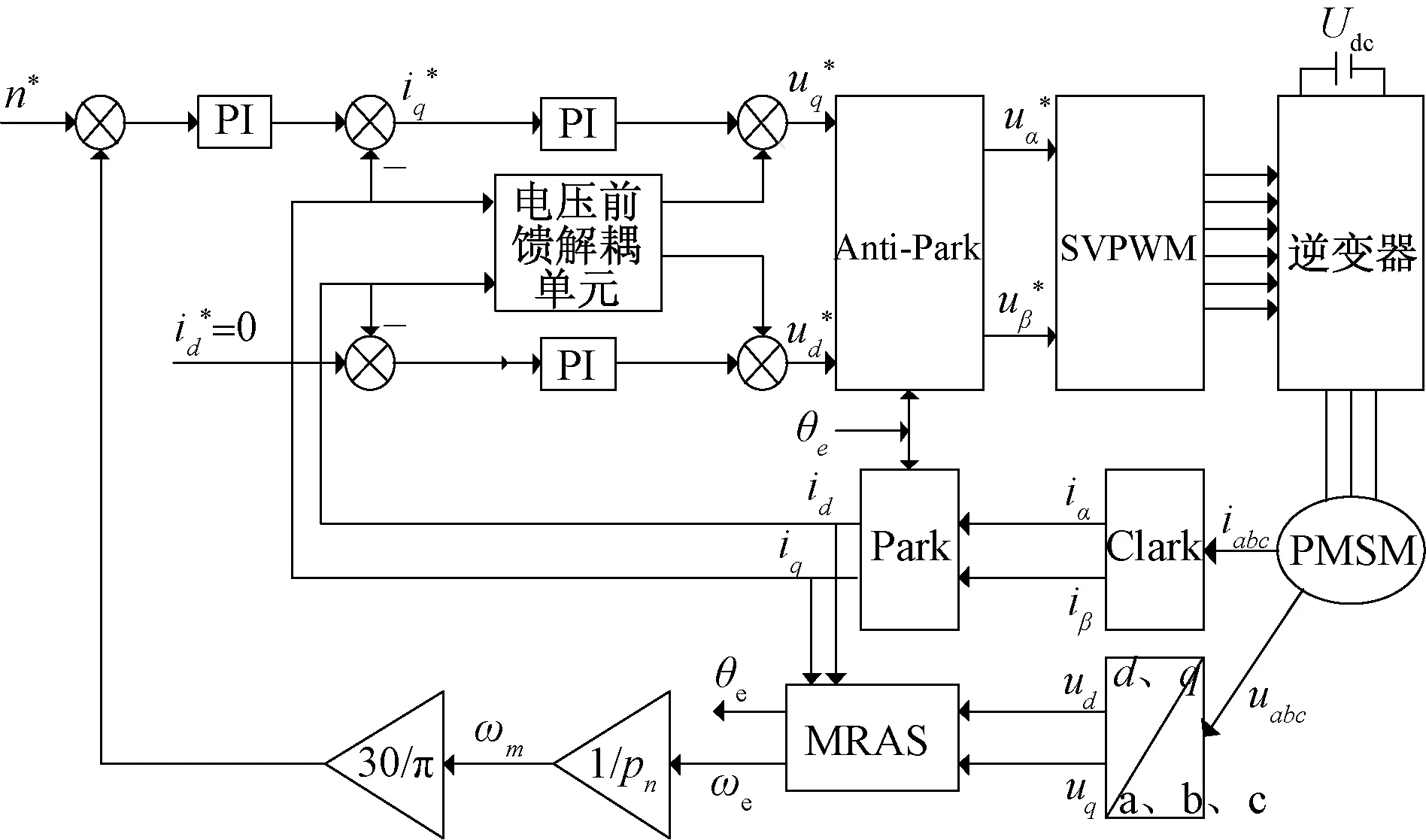
图4 带有前馈控制的MRAS的三相PMSM 矢量控制系统结构框图
根据图4的带有前馈解耦控制单元的MRAS三相PMSM无传感器控制结构框图,搭建MATLAB/SIMULINK仿真模型。其中,PWM周期为0.000 1 s。仿真中电机参数为:极对数Pn=4,定子电感Ls=8.5 mH,定子电阻R=2.875 Ω,磁链Flux=0.175 Wb,转动惯量J=4.8×10-6kg·m2。
传统控制系统中PI电流控制器分别对d轴和q轴的电流实行闭环控制,但是这种方法忽视了它们之间的相互耦合影响,降低了控制系统的动静态特性,所以本文又设计了结合常规PI调节器与电压前馈解耦单元的方法,以此来改善系统的动静态特性。
给定转速设置为600 r/min,空载和负载条件下的MATLAB仿真结果及分析如下所示:图5~图8为空载运行,图9和图10为运行在0.1 s时的加负载10 N·m。
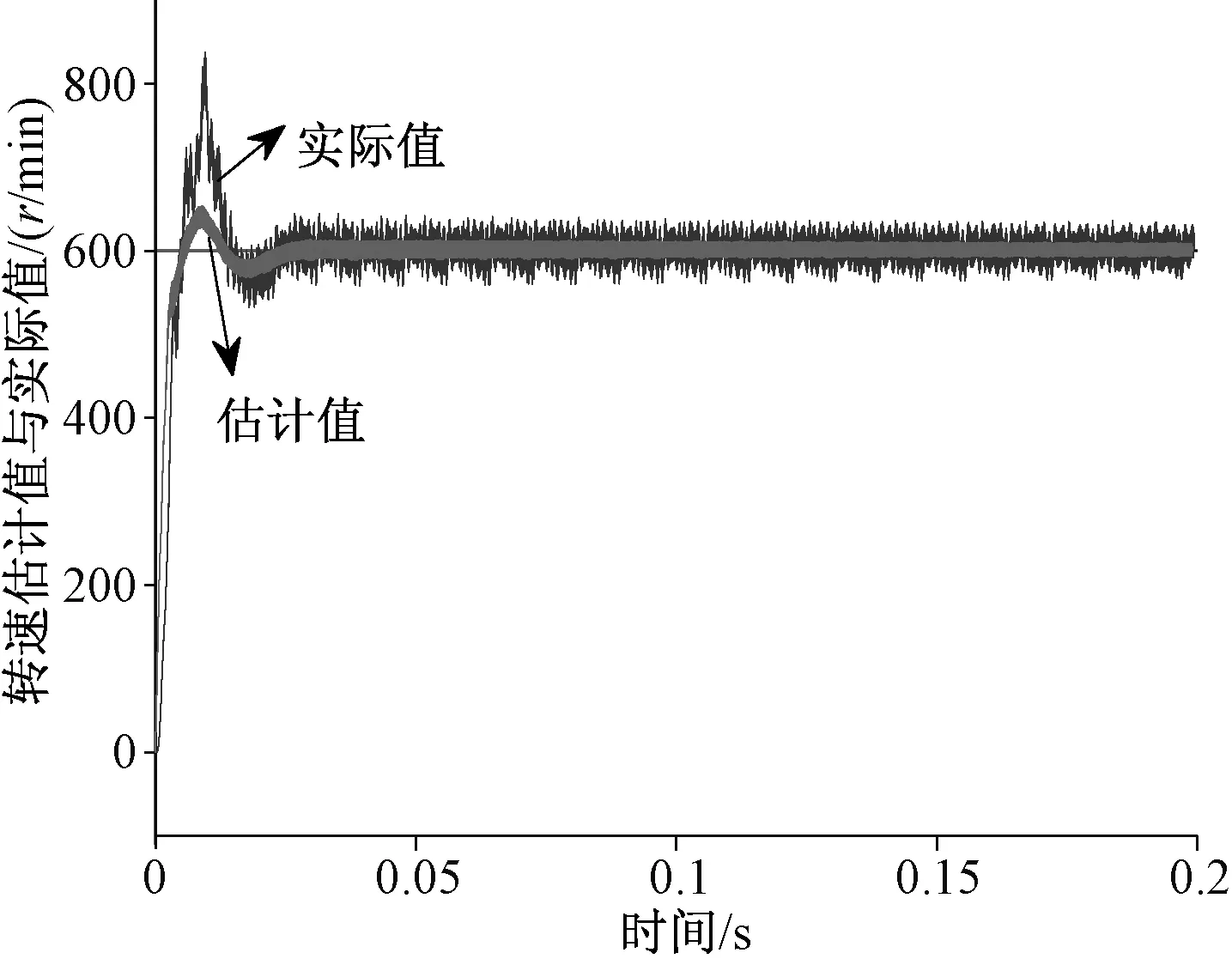
图5 转速估计值与实际值
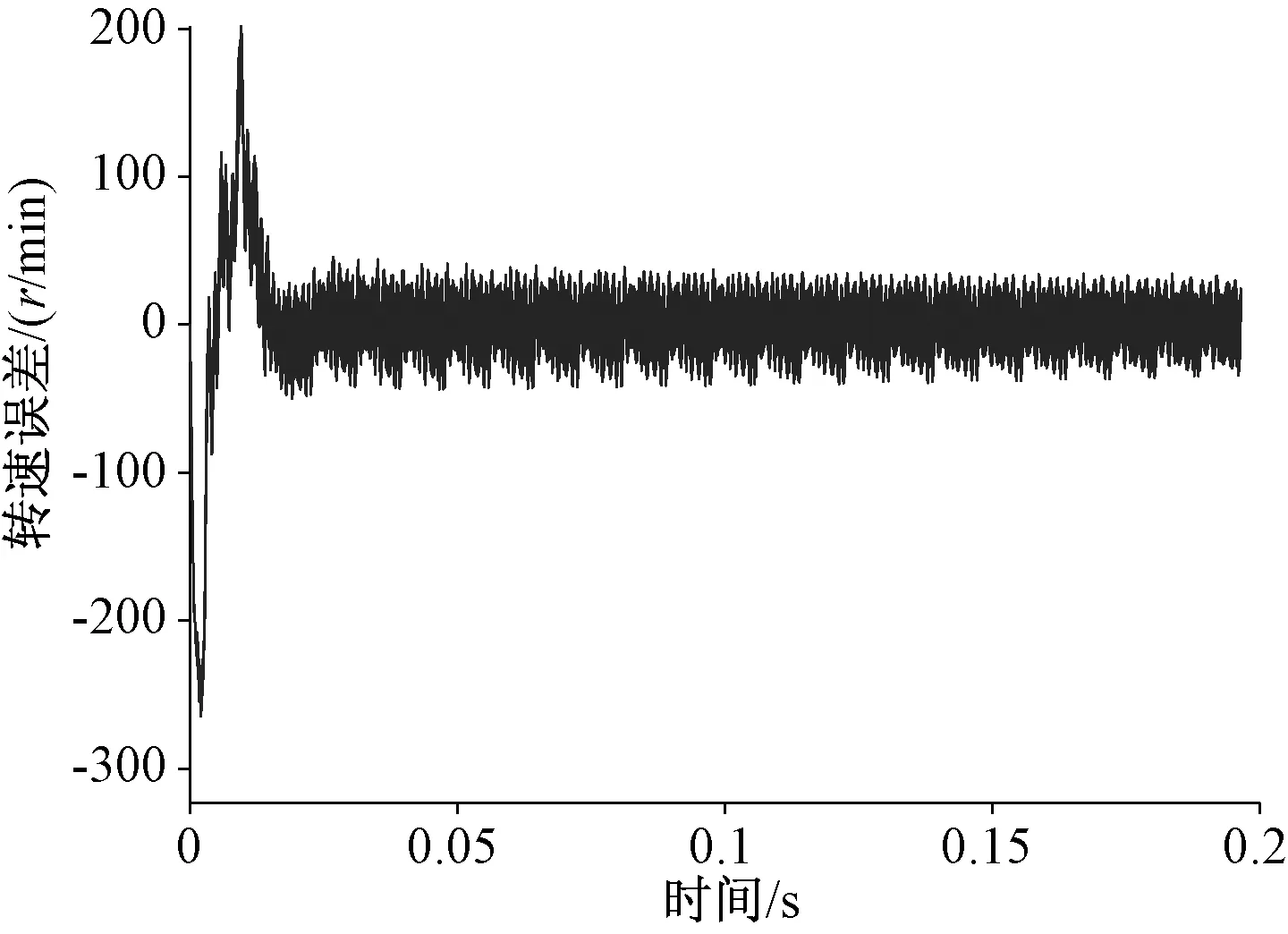
图6 转速误差

图7 转子位置的估算值与实测值
图5为PMSM转速估算值与实测值的变化曲线,图6为PMSM转速估算误差变化曲线。从图中可以看出,电机速度从零速上升到参考转速600 r/min过程中,转速估计值的变化趋势与转速实际值变化趋势基本一致。在电机转速上升阶段,转速的估算误差较大,但当转速上升到参考值并稳定运行后,转速估算误差开始渐渐减小,直至保持稳定。
图7为PMSM转子位置估算值与实测值的变化曲线,图8为PMSM转子位置估算误差的变化曲线。从仿真的结果图可以看出,电机转子的位置估算值一直紧随转子的位置实际测量值,在电机速度上升阶段,电机转子位置估计误差较大,在 -0.26 rad到0.02 rad之间,随着电机转速上升且稳定运行后,转子位置的估算误差逐渐减小,接近于零,且保持稳定。
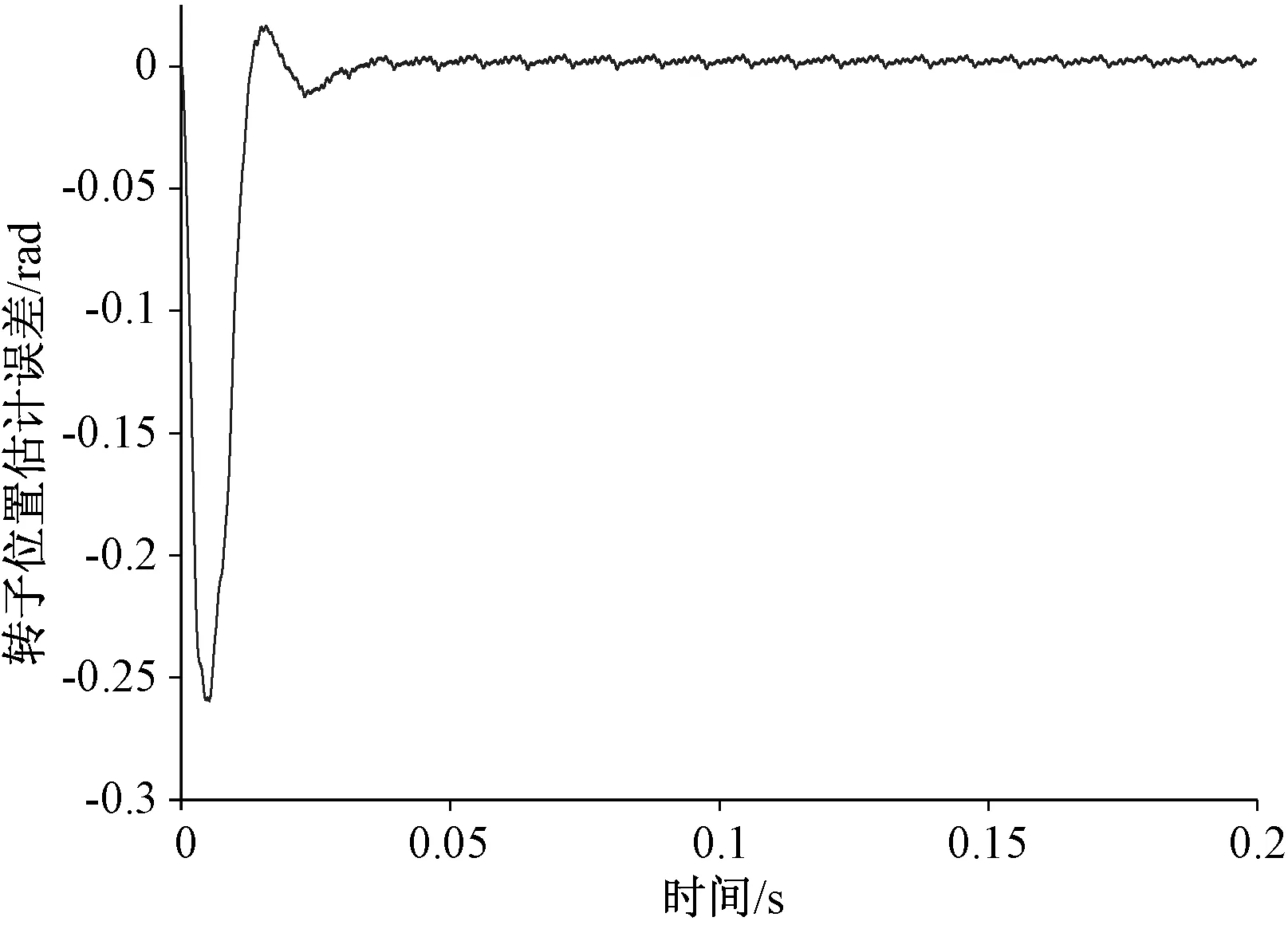
图8 转子位置估计误差
图9为负载条件下PMSM转速估算误差变化曲线。图10为负载条件下PMSM转子位置估算误差的变化曲线。从仿真结果可以看出,在刚加负载时,转速估算误差和电机转子位置估计误差都有一些波动,但是系统调节较快,两个误差都逐渐减小,直至保持稳定。

图9 转速误差(负载)
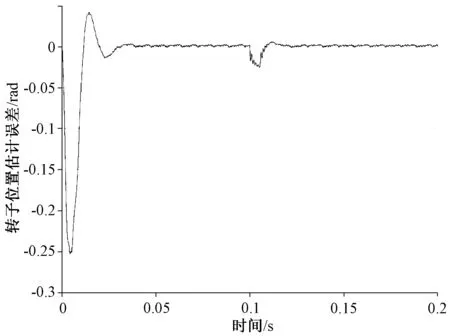
图10 转子位置估计误差(负载)
从以上的仿真结果可以表明,带有前馈解耦控制单元的MRAS无传感器的矢量控制技术能够满足实际电机控制性能的要求。
3 结论
由原理推导及仿真结果分析可知,本文提出的把MRAS和前馈解耦控制单元结合起来,应用于PMSM矢量控制系统中,再通过设计适宜的自适应律来对电机的未知参数进行识别,获得有关的转子位置和速度是可行的。通过电压前馈解耦控制单元,并利用交直轴电流调节器对其进行补偿,达到d-q轴电流的解耦的目的,并以此改善控制系统的动静态特性。经过仿真模型的验证,也最终证实了本文所提出的方法的转子位置及转速的计算精度高,系统稳定性好,响应快,能够满足实际电机控制的需求,可以替代光电编码器。
参考文献:
[1] 王鑫,李伟力,程树康.永磁同步电动机发展展望[J].微电机,2007,40(5):69-72.
[2] LIANG YAN,LI YONGDONG. Sensorless control of PM synchronous motors based on MRAS method and initial position estimation[J]. Electrical Machine sand Systems,2003,(1):96-9.
[3] 敬华兵,廖力清.基于模型参考自适应方法的无速度传感器永磁同步电机控制.机车电传动[J],2007,4(1):33-36.
[4] 尚喆,赵荣祥,窦汝振.基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J].中国电机工程学报,2007,22(4):17-23.
[5] 齐放,邓智泉,仇志坚,等. 基于 MRAS 的永磁同步电机无速度传感器[J].电工技术学报,2007(22):53-57.
[6] 李崇坚. 交流同步电机调速系统 [M]. 北京:科学出版社,2013.
[7] 李永东,张猛,肖曦,等.永磁同步电机模型参考自适应无速度传感器控制方法[J]. 电气传动, 2004,34: 302-306.
[8] 王子辉,陆凯元,叶云岳.基于改进的脉冲电压注入永磁同步电机转子初始位置检测方法[J].中国电机工程学报,2011,31(36):95-101.
[9] 李冉.永磁同步电机无位置传感器运行控制技术研究[D].杭州:浙江大学, 2012.
[10] 谷善茂,何凤有,谭国俊,等.永磁同步电动机无传感器控制技术现状与发展[J].电工技术学报,2009,24(11):14-20.
[11] 马立新,范洪成,黄阳龙.永磁伺服电机模糊PID自整定SVPWM控制研究[J].电子测量技术,2016,39(6):20-23.
[12] 王飞宇,田井呈,卓克琼,等.基于改进模型参考自适应算法的永磁同步电机转动惯量辨识[J].电机与控制应用,2016,43(8):63-67.
[13] 樊英杰, 张开如, 马慧,等. 基于模糊PI永磁同步电机优化矢量控制系统的研究[J]. 电气传动, 2016, 46(3):15-19.
[14] 卞延庆, 庄海, 张颖杰. 基于模糊PI的永磁同步电机矢量控制研究[J]. 微电机, 2015, 48(11):62-66.
[15] 张洪帅, 王平, 韩邦成. 基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J]. 中国电机工程学报, 2014, 34(12):1889-1896.

