航空重力向上延拓的外部精度评估

蒋 涛，肖学年，党亚民，章传银，刘站科

1. 中国测绘科学研究院，北京 100830； 2. 国家测绘地理信息局第一大地测量队，陕西 西安 710054

经济高效的航空重力测量能够覆盖地面重力测量难以到达地区，可提供精确的地球重力场中、短波信息，已经成为大规模重力数据采集的主要手段。大地测量和地球物理勘探等领域需要高精度的航空重力测量数据，对航空重力空中测线数据质量进行客观评价是保证航空重力数据应用水平的重要环节。

航空重力数据的内符合精度一般采用重复测线对比和交叉点不符值分析来评价[1-5]，外符合精度则需要利用其他独立观测值进行评定[6-8]。一种评价航空重力数据外符合精度的方案是将航空重力观测值向下延拓至地面或大地水准面上，与地面重力观测进行对比检核[9-16]。该方案的问题在于向下延拓是一个数据噪声得到放大的不适定过程，无论采用何种正则化解法或平滑方法都只是在一定程度上削弱或控制向下延拓误差，与地面重力观测的对比结果必然包含向下延拓误差，其量级与飞行高度和观测噪声有关，难以真实反映航空重力空中测线观测值的精度水平。

另外一种方法是将地面重力数据向上延拓至空中，与航空重力数据进行对比。不同于向下延拓，向上延拓是非常稳定的，在没有积分边界效应的情况下，即数据范围相对于计算范围有足够的冗余，向上延拓误差主要来源于地面重力格网化插值误差和代表性误差。此外，由于重力场谱组合理论和谱权确定方法取得的最新进展[17-18]，直接利用空中重力数据，不经过显式的向下延拓，已能够稳定解算区域重力场和大地水准面。因此，如何对航空重力空中测线数据外符合精度进行客观评价值得研究。

本文介绍3种基于地面重力向上延拓的航空重力测线数据外符合精度评估方法：基于梯度、基于泊松积分和基于快速傅里叶变换(FFT)的地面重力向上延拓。基于这3种方法，提出交叉检验方法估计地面重力数据误差及其空中误差传播，对毛乌素测区的航空重力空中测线数据进行外符合精度评价。

1 基于梯度的地面重力向上延拓

若在航空重力测区布设有密集的地面重力点，由于地面重力观测精度高，可利用地面重力数据对航空重力空中测线观测值的精度进行验证。一种方法是将地面重力扰动向上延拓至空中，与实测空中测线重力扰动进行比较。航空重力测量中采用差分GNSS动态定位方式获取测线采样点处的大地高，因此本文中的测线重力观测值均为重力扰动，而不是重力异常。

地面重力扰动向上延拓可采用梯度法，计算地面重力扰动沿椭球法线方向上的梯度，按照点对点延拓方式将地面重力扰动向上延拓至空中。空中与地面重力扰动满足如下Taylor级数展开式

(1)

(2)

式中，l0为计算点到流动点的空间距离。式(2)属于积分计算，应先将地面重力扰动格网化后再代入计算。

地面重力点数量一般远小于航空重力测线点数量，因此需要将航空重力测线观测值内插到地面重力的空中延拓点处，再对二者做差

Δ=δgair-δgTerU

(3)

2 基于泊松积分的地面重力向上延拓

除了基于梯度的点对点向上延拓外，还可利用泊松积分将地面重力数据向上延拓至空中测线处[19]。理论上泊松积分需要输入全球均匀分布的数据，但实际中地面重力数据仅覆盖局部区域，因此一般需采用移去恢复法进行计算，选定某个地球重力场模型作为参考重力场，地面重力数据覆盖范围以外由重力场模型贡献，高频地形影响采用残余地形模型(RTM)方法计算[20]。移去恢复法的另外一个优势在于，移去参考重力场和高频地形影响后的残余地面重力扰动量级很小，在格网化插值、泊松积分计算时引入的误差也很小。

(4)

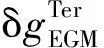
(5)

式中，ρ为平均地形密度；(xP,yP,zP)和(x,y,z)分别为计算点与流动点的局部直角坐标；HP为计算点的真实地形高度；HRef为计算点的平均地形高度。

图1描述了基于泊松积分的地面重力数据向上延拓原理。地面重力数据分布在具有地形起伏的地球表面，需将地面重力扰动解析延拓归算到当地平均地形高度面上。首先利用式(2)由残余地面重力扰动计算得到梯度，再根据地面重力点与平均地形高度面之间的高度差，类似于式(1)计算解析延拓改正量，将残余地面重力扰动统一归算到当地平均地形高度面。

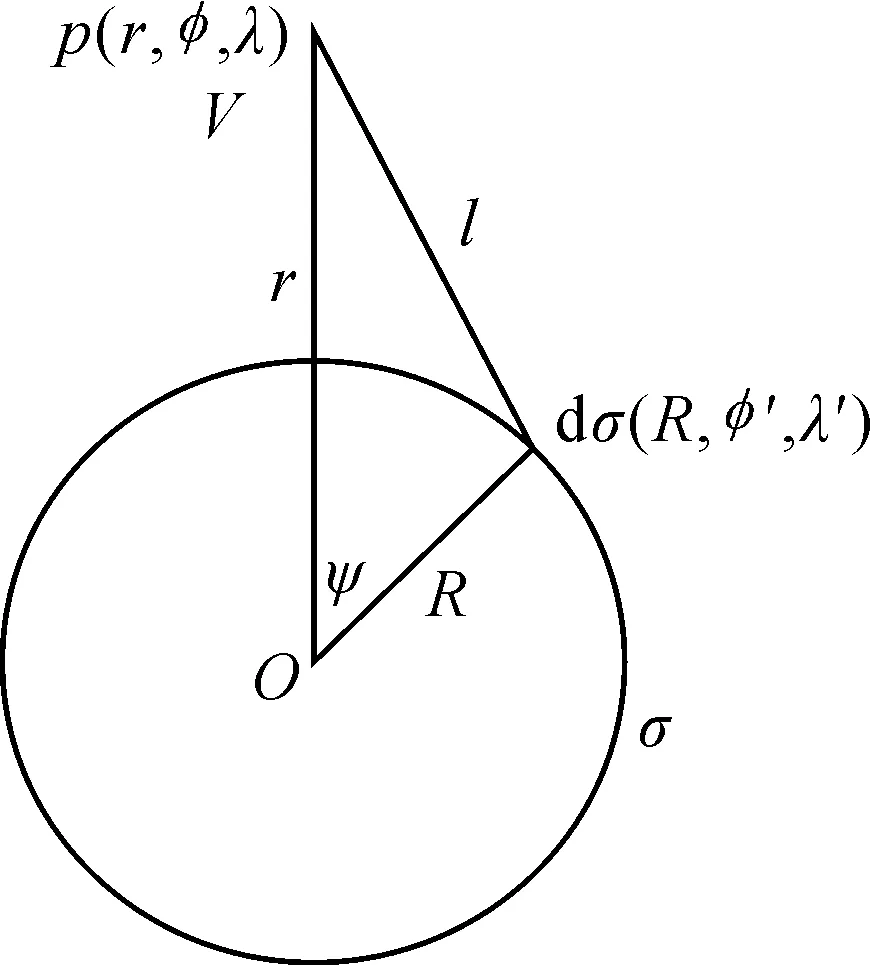
图1 基于泊松积分的地面重力向上延拓示意图Fig.1 Schematic diagram of the terrestrial gravity UPC based on Poisson integral

(6)

R=RE+hM

(7)

r=RE+h′

(8)

式中，RE为地球平均半径；hM为地面点的平均大地高；h′为空中点的大地高；σ表示单位球积分区域；dσ=cosφ′dφ′dλ′为单位球积分面元；l为球面σ上的流动点到空中计算点的距离。

残余地面重力扰动向上延拓到空中后，还需要在空中点位处恢复参考重力场模型和高频地形影响的贡献，得到最终的地面重力扰动向上延拓值δgTerU

(9)

3 基于FFT的地面重力向上延拓

在平面直角坐标系中，泊松积分公式写为

δg(x,y,Δh)=

(10)

式中,(x,y)表示平面坐标；Δh为向上延拓高度，即平均地形高度面到平均飞行高度面的距离。式(10)可写成空域内卷积的形式[21]

δg(x,y,Δh)=w(x,y)*δg(x′,y′,0)

(11)

式中，*为卷积号；w(x,y)为泊松核

(12)

利用快速傅里叶变换(FFT)将空域内的卷积化为频域内的乘积

F2{δg(x,y,Δh)}=W(u,v)F2{δg(x′,y′,0)}

(13)

式中，F2表示二维傅里叶变换；W(u,v)为泊松核在频域内的表达式

(14)

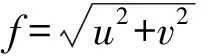
因此在频域内重力扰动向上延拓表达为

(15)

4 地面重力误差估计及其空中传播

在飞行高度处，航空重力扰动与地面重力扰动向上延拓值之间的差值由航空重力数据误差和地面重力向上延拓值误差两部分构成。地面重力向上延拓值误差主要来源于：①单点地面重力测量误差；②地面重力解析延拓误差，即将地球表面的重力观测值归算到平均地形高度面引起的误差；③地面重力格网插值误差，即对地面重力数据进行格网化产生的插值误差；④地面重力代表性误差，即用格网平均值代替离散点值引起的代表性误差[22]；⑤向上延拓方法本身引起的误差。此外，若数据范围有限，靠近数据范围边界的计算点还会受到边界效应的影响。

单点地面重力测量误差为10～20 μGal，可以忽略不计。由于采用了移去恢复法，残余地面重力扰动量级很小，地面重力解析延拓误差也可忽略[23]。边缘计算点的边界效应可采用扩大数据点范围或内缩计算点范围的方式来消除。因此，为了估算航空重力数据误差，需要分离的主要是地面重力格网插值误差和代表性误差在飞行高度处的影响。

地面重力格网插值误差和代表性误差可采用交叉检验法进行估计。具体方法是：若欲估计某个地面重力点的误差，先利用所有离散地面重力点格网化得到重力格网，再由重力格网内插得到该观测点处的内插重力值，原始重力值与内插重力值之差τ为

τ=δgOri-δgInt

(16)

式中，δgOri为原始重力扰动值；δgInt为内插重力扰动值；差值τ近似由地面重力格网插值误差和代表性误差组成。

利用交叉检验法得到地面重力格网插值误差和代表性误差后，还需要利用向上延拓方法得到飞行高度处的地面重力误差影响。根据误差传播定律，扣除地面重力误差影响后，空中航空重力扰动数据的中误差可表示为

(17)

式中，σΔ为航空重力与地面重力向上延拓值互差的标准差；στ为地面重力误差向上延拓传播到空中点后的标准差。图2为航空重力数据误差估计的流程。

5 毛乌素测区航空重力空中测线数据外符合精度评价

5.1 测区和数据情况

2015年4月17日至6月11日，国家测绘地理信息局第一大地测量队在毛乌素地区开展了航空重力测量试验性项目。毛乌素测区位于陕西与内蒙古交界处，地貌以沙漠丘陵为主，地形起伏如图3所示，绘图采用SRTM数字高程模型数据[24]，该区域平均地形高度1248 m，最小高度730 m，最大高度2420 m。飞机选用塞斯纳208机型，机上搭载GT-2A航空重力测量系统和1台Ashtech双频GPS接收机，地面架设2个GPS基准站。选取鄂尔多斯机场作为飞机起降保障机场，机场距毛乌素测区的飞行距离约为80 km。

图2 航空重力数据误差估计流程Fig.2 Flow chart of airborne gravity error estimation

航空重力空中测线覆盖范围为纬线(38.77°N—39.32°N)和经线(109.23°E—110.52°E)围成的区域，布设有32条测线，其中东西方向11条，南北方向21条，平均飞行高度为2087 m，平均飞行速度约260 km/h，数据采样率为2 Hz，测线间距为5 km，共包含71 773个数据点，测线数据采用100 s的卡尔曼滤波消除高频噪声。在地面上按照5 km平均间距布设了459个地面重力点，向航空重力数据范围四周各延伸10 km，覆盖范围为纬线(38.67°N—39.41°N)和经线(109.12°E—110.63°E)围成的区域。在每个地面重力点上实施了约30 min的GPS静态定位观测以测定其大地高，GPS数据处理采用WayPoint软件，与附近的IGS站点组网解算得到地面点坐标，大地高精度约为10 cm，按照索米里安公式[19]严密计算观测点处的正常重力值，参考椭球选取CGCS2000椭球。航空重力测线与地面重力点的空间分布如图4所示，其中绿线为航空重力空中测线，红点为地面重力点。表1列出了航空和地面重力扰动观测值的统计信息。

表1航空与地面重力扰动统计

Tab.1StatisticsofterrestrialandairbornegravitydisturbancesmGal

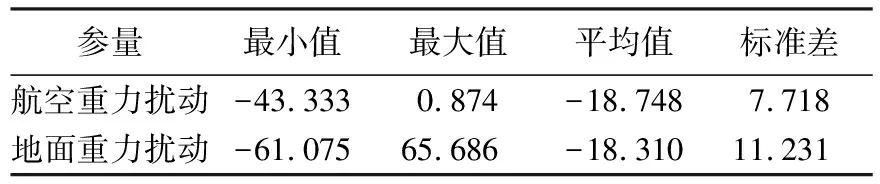
参量最小值最大值平均值标准差航空重力扰动-43.3330.874-18.7487.718地面重力扰动-61.07565.686-18.31011.231

5.2 地面重力误差估计及其空中传播

利用交叉检验法估算地面重力数据的格网插值误差和代表性误差，格网化方法选取反距离加权插值，选择这一方法的原因是毛乌素测区的地面重力点分布比较合理、密集，简单的反距离加权插值即可达到较好的格网化效果，另外该方法对数据的处理较为简单，对数据的干预少，更能保持数据本身的特性。对459个地面点进行反距离加权插值格网化，得到2′×2′重力扰动格网，再内插到离散观测点处，将内插重力扰动与原始重力扰动做差得到地面重力误差估值。分别采用梯度法、泊松积分法和FFT法，计算得到地面重力误差对空中点的影响，其中泊松积分法和FFT法需要先将地面重力离散点的误差估值格网化得到2′×2′误差格网。表2列出了地面重力扰动误差估计和3种方法空中误差传播的统计信息，地面重力数据误差的标准差为1.69 mGal，向上延拓传播到空中点的误差影响分别为0.66、0.78和0.92 mGal，不能忽略。图5—图7分别绘制了3种向上延拓方法所得地面重力扰动误差对空中点的影响。

表2地面重力扰动误差及其空中传播

Tab.2StatisticsoftheerrorestimatesandpropagationofterrestrialgravitydisturbancesmGal

高度面方法点数最小值最大值平均值标准差地面点误差交叉检验法459-16.138.720.001.69空中点误差梯度法459-6.851.68-0.050.66泊松积分法71773-8.572.32-0.130.78FFT法71773-7.953.28-0.120.92

5.3 航空重力数据外符合精度

利用3种向上延拓方案，对毛乌素航空重力空中测线重力扰动观测值的外符合精度进行评价。第1种方案是利用梯度法将地面重力扰动向上延拓至空中相应点位，将航空重力测线重力扰动内插到空中延拓点处，内插值与地面重力扰动向上延拓值进行比较，式(1)中的梯度直接采用2′×2′地面重力扰动按照式(2)计算，积分半径选取0.5°。第2种方案是利用泊松积分法将地面重力扰动向上延拓至空中测线处，再将航空重力测线重力扰动与地面重力扰动向上延拓值进行比较，泊松积分计算采用移去恢复法，球冠积分半径选取0.5°，参考重力场模型选取EIGEN-6C4[25]，地形数据采用3″分辨率的SRTM数字高程模型[26]。第3种方案是利用FFT方法将地面重力扰动向上延拓至空中，采用与方案2相同的移去恢复处理。基于这3种向上延拓方案，航空重力扰动与地面重力扰动空中延拓值的差值统计信息见表3。图8—图10分别绘制了3种向上延拓方案所得航空与地面重力扰动的差值。如前所述，表3中的差值主要包括航空重力数据误差和地面重力误差影响，采用式(17)扣除地面重力误差影响，3种向上延拓方案得到航空重力数据的中误差分别为4.7、2.94和2.83 mGal。可以看出，扣除了地面重力误差影响后，在航空与地面重力扰动差值的基础上，3种方案估计得到的航空重力扰动误差均有所减小，梯度法所得误差最大，泊松积分法与FFT法非常接近。

表3航空重力扰动与地面重力向上延拓值的差值统计

Tab.3StatisticsofdifferencesbetweenairbornegravitydisturbancesandUPCvaluesofterrestrialgravitymGal

向上延拓方案点数最小值最大值平均值标准差梯度法459-35.7517.150.744.75泊松积分法71773-28.628.020.013.04FFT法71773-27.127.33-0.042.98

毛乌素测区数据范围在纬线方向跨越0.74°、经线方向横跨1.51°，泊松积分公式的球冠积分半径选取为0.5°，因此上述对比结果不可避免地包含了因数据范围有限导致的边界效应，见图8—10。为对航空重力测线观测值精度进行准确评估，需消除因地面重力向上延拓带来的边界效应，但因为毛乌素测区地面重力数据范围有限，本文试验中无法完全消除边界效应，只能削弱其影响。在数据点范围基础上，将参与对比的计算点范围内缩，可削弱边界效应。图8—图10中的矩形区域为内缩后的对比计算点范围。表4分别列出了3种方案内缩计算范围后航空重力扰动与地面重力向上延拓值的差值统计信息。可以看出，3种方案的对比结果均受到边界效应的影响，梯度法的边界效应更为显著。将计算点范围在纬向内缩0.1°、经向内缩0.25°后，航空与地面重力的差值显著减小。在内缩后的区域，地面重力误差向上延拓传播到空中点后的标准差分别为0.31、0.59和0.71 mGal。结合表4，利用式(17)扣除地面重力误差影响，3种向上延拓方案所得航空重力数据的中误差分别为1.62、1.5和1.42 mGal。

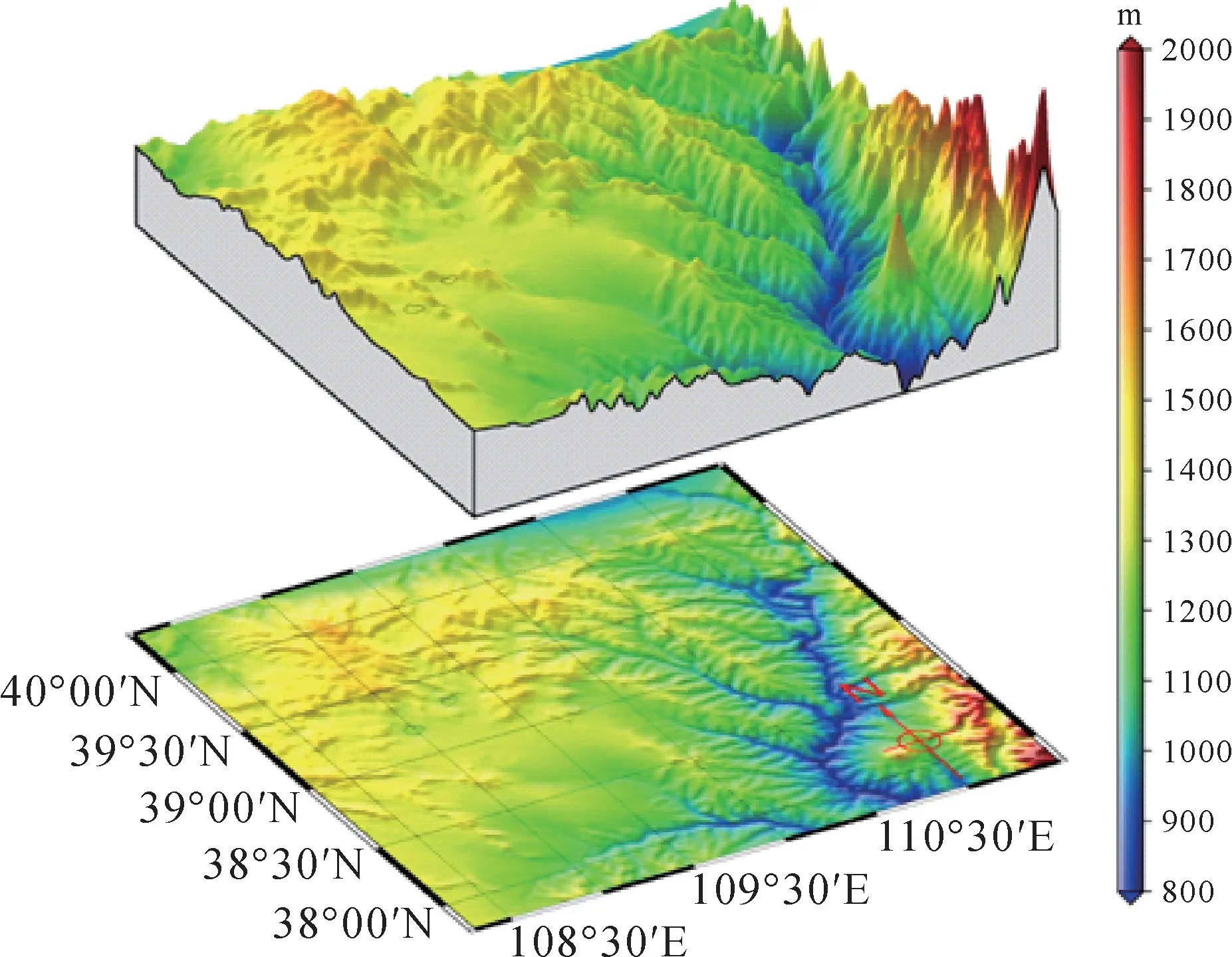
图3 毛乌素测区SRTM地形起伏图Fig.3 SRTM topography of Mu Us area

图4 毛乌素测区地面重力数据与航空重力测线分布图Fig.4 Distribution of terrestrial gravity and airborne gravity survey lines over Mu Us area

图5 梯度法的地面重力扰动误差空中传播Fig.5 Error propagation of ground gravity disturbance error at flight altitude of gradient method

图6 泊松积分法的地面重力扰动误差空中传播Fig.6 Error propagation of ground gravity disturbance error at flight altitude of Poisson integral method

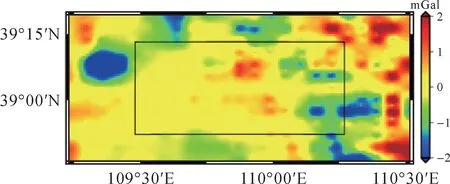
图7 FFT法的地面重力扰动误差空中传播Fig.7 Error propagation of ground gravity disturbance error at flight altitude of FFT method

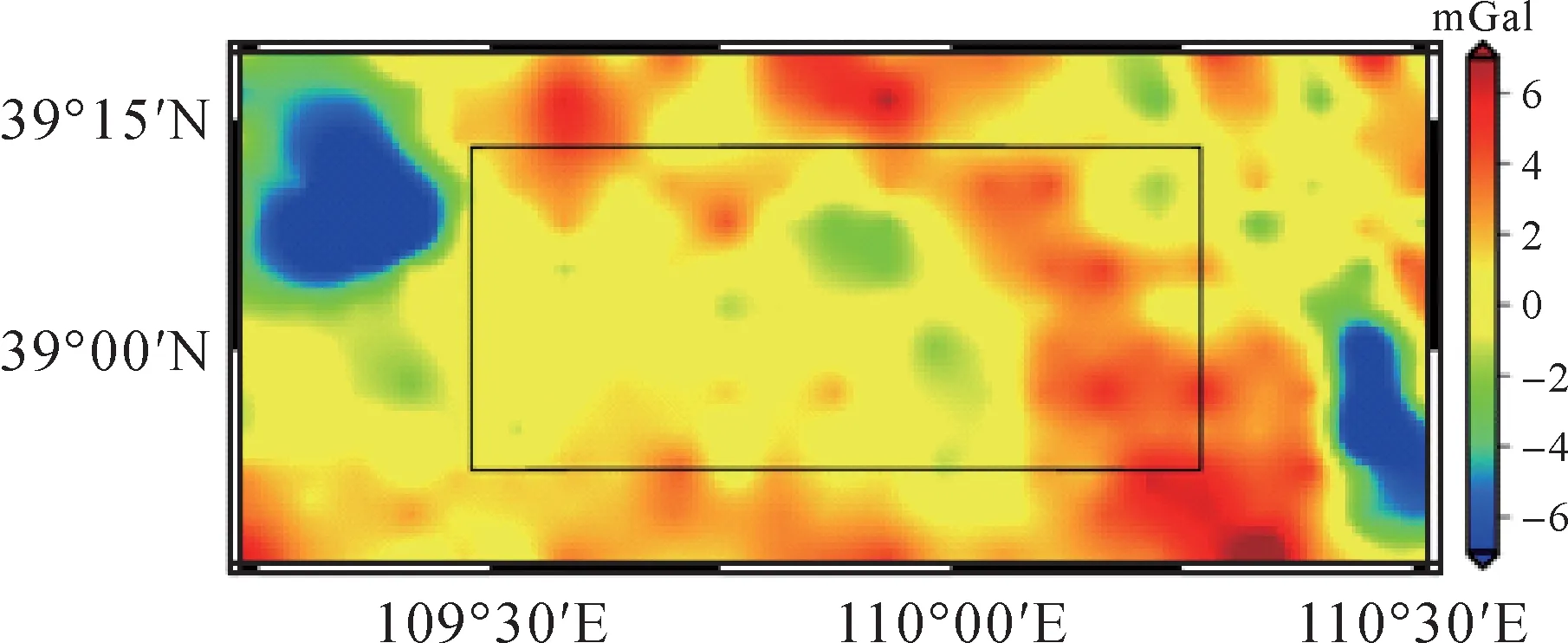
图8 梯度法结果Fig.8 Results of gradient method

图9 泊松积分法结果Fig.9 Results of Poisson integral method

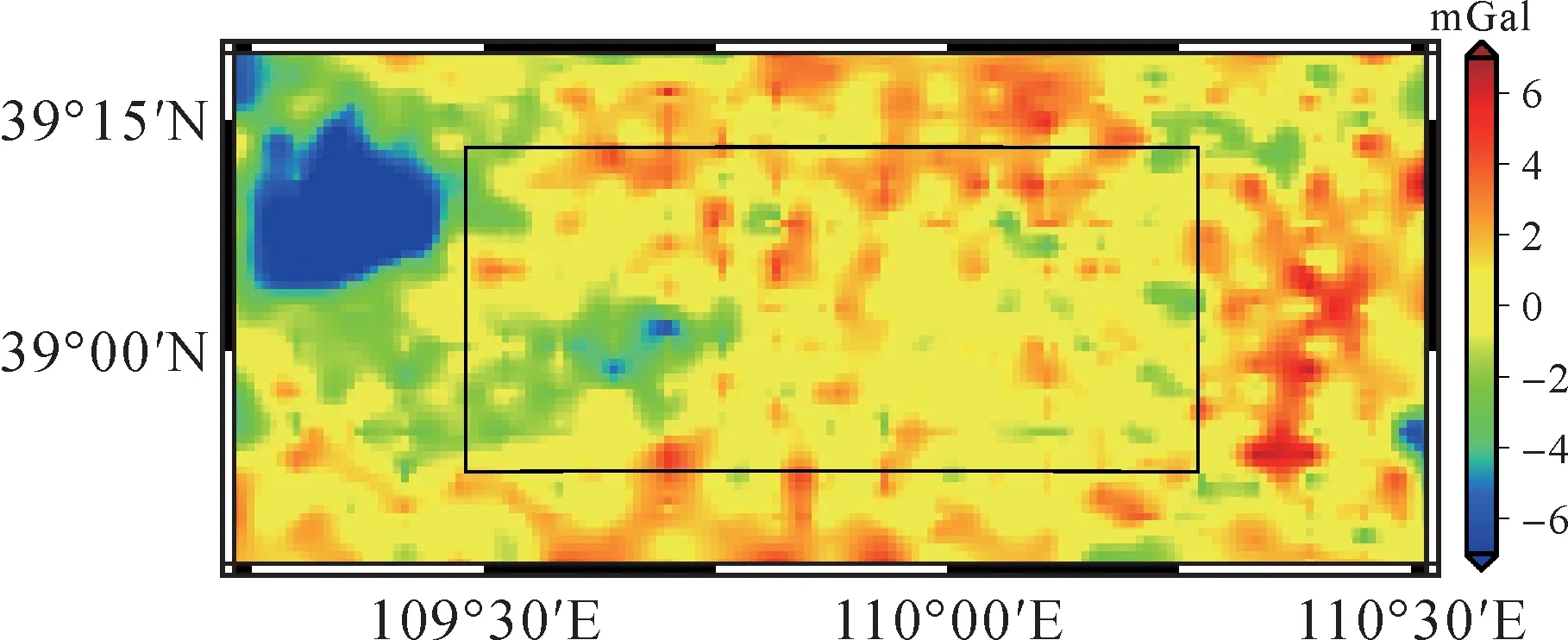
图10 FFT法结果Fig.10 Results of FFT method

需要指出的是，这一内缩处理无法完全消除边界效应，只是在一定程度上削弱了边界效应，估计得到的航空重力数据误差中还包含有残余边界效应。此外，从表4中的平均差值可以看出，毛乌素测区的航空重力与地面重力数据之间基本不存在系统偏差，这对于GT-2A航空重力数据的后续应用，如大地水准面建模是非常有益的。

表4内缩计算范围后航空重力扰动与地面重力向上延拓值的差值统计

Tab.4StatisticsofdifferencesbetweenairbornegravitydisturbancesandUPCvaluesofterrestrialgravityaftercomputationareareductionmGal

6 结 论

利用毛乌素测区实测航空和地面重力数据，分别对基于梯度、基于泊松积分和基于FFT的地面重力向上延拓这3种航空重力空中测线数据外符合精度评价方法进行了对比分析，结果表明：

(1) 航空重力空中测线数据外符合精度评定必须扣除地面重力格网插值误差和代表性误差对空中点的影响，交叉检验法可有效估计这两项主要误差影响。毛乌素测区地面重力数据误差的标准差为1.69 mGal，采用3种向上延拓方案传播到空中点的误差影响分别为0.66 mGal、0.78 mGal和0.92 mGal，不能忽略。

(2) 基于泊松积分和基于FFT的地面重力向上延拓方案均能够客观评价航空重力空中测线观测值的外符合精度，二者表现相当，梯度法表现稍差。在包含残余边界效应的情况下，扣除地面重力误差影响后，毛乌素测区GT-2A航空重力空中测线重力扰动的外符合精度优于1.42 mGal。

(3) GT-2A航空重力观测值与地面重力观测值之间的系统偏差很小，这对大地水准面建模等航空重力数据的后期应用是非常有益的。

参考文献：

[1] HWANG C, HSIAO Y S, SHIH H C. Data Reduction in Scalar Airborne Gravimetry: Theory, Software and Case Study in Taiwan[J]. Computers & Geosciences, 2006, 32(10): 1573-1584.

[2] 郭志宏, 熊盛青, 周坚鑫, 等. 航空重力重复线测试数据质量评价方法研究[J]. 地球物理学报, 2008, 51(5): 1538-1543.

GUO Zhihong, XIONG Shengqing, ZHOU Jianxin, et al. The Research on Quality Evaluation Method of Test Repeat Lines in Airborne Gravity Survey[J]. Chinese Journal of Geophysics, 2008, 51(5): 1538-1543.

[3] 蒋涛. 利用航空重力测量数据确定区域大地水准面[J]. 测绘学报, 2013, 42(1): 152.

JIANG Tao. Regional Geoid Determination Using Airborne Gravimetry Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 152.

[4] 欧阳永忠, 邓凯亮, 陆秀平, 等. 多型航空重力仪同机测试及其数据分析[J]. 海洋测绘, 2013, 33(4): 6-11.

OUYANG Yongzhong, DENG Kailiang, LU Xiuping, et al. Tests of Multi-type Airborne Gravimeters and Data Analysis[J]. Hydrographic Surveying and Charting, 2013, 33(4): 6-11.

[5] 孙中苗, 翟振和, 肖云. 渤海湾航空重力及其在海域大地水准面精化中的应用[J]. 测绘学报, 2014, 43(11): 1101-1108. DOI: 10.13485/j.cnki.11-208.

SUN Zhongmiao, ZHAI Zhenhe, XIAO Yun. Airborne Gravimetry in Bo Hai Bay and Its Role on the Refining of the Regional Marine Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1101-1108. DOI: 10.13485/j.cnki.11-208.

[6] 孙中苗, 夏哲仁, 李迎春, 等. 中等山区航空重力测量的精度分析[J]. 大地测量与地球动力学, 2009, 29(2): 53-56, 65.

SUN Zhongmiao, XIA Zheren, LI Yingchun, et al. Accuracy Evaluation of Airborne Gravimetry over Moderate Mountain Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 53-56, 65.

[7] 孙中苗, 翟振和, 李迎春. 航空重力测量的分辨率和精度分析[J]. 地球物理学进展, 2010, 25(3): 795-798.

SUN Zhongmiao, ZHAI Zhenhe, LI Yingchun. Analysis on the Resolution and Accuracy of Airborne Gravity Survey[J]. Progress in Geophysics, 2010, 25(3): 795-798.

[8] 翟振和, 孙中苗, 李迎春, 等. 航空重力测量在近海区域的精度评估与分析[J]. 测绘学报, 2015, 44(1): 1-5. DOI: 10.11947/j.AGCS.2015.20130783.

ZHAI Zhenhe, SUN Zhongmiao, LI Yingchun, et al. The Accuracy Evaluation and Analysis of Airborne Gravimetry in Coastal Area[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 1-5. DOI: 10.11947/j.AGCS.2015.20130783.

[9] 王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及其谱分解[J]. 测绘学报, 2004, 33(1): 33-38.

WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 33-38.

[10] 顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J]. 测绘学报, 2010, 39(5): 458-464.

GU Yongwei, GUI Qingming. Study of Regularization Based on Signal-to-Noise Index in Airborne Gravity Downward to the Earth Surface[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 458-464.

[11] 邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报, 2011, 40(6): 690-696.

DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regularization Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 690-696.

[12] 蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011, 40(6): 684-689.

JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. The Solution of Ill-Posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 684-689.

[13] 蒋涛, 党亚民, 章传银, 等. 基于矩谐分析的航空重力向下延拓[J]. 测绘学报, 2013, 42(4): 475-480.

JIANG Tao, DANG Yamin, ZHANG Chuanyin, et al. Downward Continuation of Airborne Gravity Data Based on Rectangular Harmonic Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 475-480.

[14] 蒋涛, 李建成, 党亚民, 等. 基于矩谐分析的区域重力场建模[J]. 中国科学: 地球科学, 2014, 44(1): 82-89.

JIANG Tao, LI Jiancheng, DANG Yamin, et al. Regional Gravity Field Modeling Based on Rectangular Harmonic Analysis[J]. Science China：Earth Sciences, 2014,42(4):82-89.

[15] JIANG Tao, LI Jiancheng, DANG Yamin, et al. Regional Gravity Field Modeling Based on Rectangular Harmonic Analysis[J]. Science China Earth Sciences, 2014, 57(7): 1637-1644.

[16] 刘敏, 黄谟涛, 欧阳永忠, 等. 顾及地形效应的重力向下延拓模型分析与检验[J]. 测绘学报, 2016, 45(5): 521-530. DOI: 10.11947/j.agcs.2016.20150453.

LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Test and Analysis of Downward Continuation Models for Airborne Gravity Data with Regard to the Effect of Topographic Height[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 521-530. DOI: 10.11947/j.agcs.2016.20150453.

[17] JIANG Tao, WANG Yanming. On the Spectral Combination of Satellite Gravity Model, Terrestrial and Airborne Gravity Data for Local Gravimetric Geoid Computation[J]. Journal of Geodesy, 2016, 90(12): 1405-1418.

[18] WANG Yanming, HUANG Jianliang, JIANG Tao, et al. Local Geoid Determination[M]∥GRAFAREND E. Encyclopedia of Geodesy. Cham: Springer, 2016. DOI: 10.1007/978-3-319-02370-0_53-1.

[19] HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. New York: SpringerWienNewYork, 2006.

[20] FORSBERG R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling[R]. Reports of the Department of Geodetic Science and Surveying, 1984, #355. Columbus, Ohio: The Ohio State University, 1984.

[21] LI Yecai. Airborne Gravimetry for Geoid Determination[D]. Calgary: University of Calgary, 2000.

[22] 陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.

LU Zhonglian. Theory and Method of Earth’s Gravity Field[M]. Beijing: The People’s Liberation Army Press, 1996.

[23] CRUZ J Y, LASKOWSKI P. Upward Continuation of Surface Gravity Anomalies[R]. Report No. 360. Columbus: The Ohio State University, Department of Geodetic Science and Surveying, 1984.

[24] FARR T G, ROSEN P A, CARO E, et al. The Shuttle Radar Topography Mission[J]. Reviews of Geophysics, 2007, 45(2): RG2004. DOI: 10.1029/2005RG000183.

[25] FÖRSTE C, BRUINSMA S L, FLECHTNER F, et al. A Preliminary Update of the Direct Approach GOCE Processing and A New Release of EIGEN-6C[C]∥AGU Fall Meeting. San Francisco: AGU Fall Meeting, 2012.