基于MBR组合优化算法的多尺度面实体匹配方法
刘凌佳,朱道也,朱欣焰,2,3,丁小辉,呙 维,2
1. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2. 武汉大学地球空间信息技术协同创新中心,湖北 武汉 430079; 3. 武汉大学空天信息安全与可信计算教育部重点实验室,湖北 武汉 430072; 4. 中国科学院东北地理与农业生态研究所,吉林 长春 130102
实体匹配是空间数据处理和应用领域的基础性研究问题[1],其定义为通过相似性指标识别出不同来源地图数据之间的同名实体,并建立对应关系的过程[2],它被广泛应用于空间数据的更新、维护和融合[3]。近年来,随着“自发地理信息(VGI)”的兴起,实体匹配又成为VGI数据质量改善和评价的关键技术[4-5]。然而不同来源的地理空间数据往往在现势性、表达尺度、几何和语义等方面不一致[6-9],导致获得精确的匹配结果成为一个的挑战,尤其是多尺度数据的匹配,因为多尺度匹配中复杂匹配(1∶N和M∶N匹配)广泛存在,且匹配数据之间的特征更为模糊[10]。因此,提出一种适用于多尺度数据的匹配方法具有重要意义。
近年来,在实体匹配领域已有许多的探索。文献[11]从匹配的特征出发提出了语义匹配、拓扑匹配和几何匹配;文献[7]提出了缓冲区增长法来获取候选匹配,然后基于通信理论的调查统计方法来匹配道路网;文献[12]通过测量目标实体与地标的位移来衡量建筑物的环境相似性,并和几何特征一并用来匹配建筑物面;文献[13]扩展了文献[12]关于环境相似度的计算方法,通过目标建筑物周围三角形的面积和周长来计算环境相似度。匹配特征可以是单一的或多元的。然而,为了获得可靠的匹配结果,多元特征组合进行匹配被普遍接受[14]。因此,一些学者尝试将实体匹配问题转化为模型分类问题以解决多元特征的权重分配和匹配阈值设置问题。文献[15]对比了决策树、朴素贝叶斯和SVM在建筑物面实体匹配中的精度;文献[16]通过神经网络决策树来匹配点、线和面实体;文献[17]引入SVM构建道路网多特征匹配模式,并用于预测未知道路网待匹配对;文献[18]利用文献[19]中面积重叠法获取候选匹配,然后引入了人工神经网络从中发现正确匹配。
尽管以上研究取得了较好的匹配精度,但需进一步改进以匹配多尺度数据。在这些研究中,通常采用缓冲区增长法和面积重叠法来获取候选匹配,文献[20]还开发了依据面积重叠获取邻接矩阵,然后利用邻接矩阵运算确定多对多匹配候选的方法。然而,缓冲区增长法只能获取1∶1匹配候选,其不能确定缓冲区内哪些要素需聚合起来进行匹配;面积重叠法在空间数据存在较大位移偏差时是完全无用的[14],如图1所示,a2、a3与b1错误重叠。由于存在人为主观认识差异和地理实体空间不确定性[21],即使通过投影转换、格式转换和地图纠正等预处理,匹配实体也只是粗糙对齐,坐标偏差依然存在,这将导致大量的正确匹配被漏选,面积较小的实体被忽略。
为了解决以上问题,本文提出依据形状特征来确定候选匹配的方法。形状特征是衡量同名实体的重要指标[22-23],对于1∶N和M∶N匹配,其整体上也存在轮廓和结构上的相似性[24]。然而,直接通过要素的随机组合获取聚合要素集的形状特征来确定候选匹配,其计算量过大。为此本文将实体简化为最小外包矩形来代替,并结合回溯算法来提高搜索效率,定义所提出的获取候选匹配的算法为MBR组合优化算法。本文还将距离、大小、方向和形状特征与人工神经网络结合,各特征的权重由智能学习确定,以预测被调查候选匹配的匹配概率并评估其是否匹配。
1 基于MBR组合优化算法的面实体匹配方法
1.1 MBR组合优化算法
确定候选匹配是实体匹配的重要环节,其目的是通过粗略分析以限制潜在相似特征的数量,以此来减少匹配耗时[7,25]。对于待匹配面要素a,通过缓冲分析获取a的n个候选要素Ba={b1,b2,…,bn}。若a为一对一或一对多的匹配关系,需搜索b中哪一个要素或哪一些要素与a存在潜在的对应关系。最直接的方法是使用穷举法获取所有的组合,然后比较要素组合与a的形状特征是否相似来筛选潜在匹配。然而,穷举法计算量过大(2n个组合),虽精度较高但形状描述子(如转角函数、几何矩、傅里叶等)计算很复杂,所以当n过大时,穷举法并不可行。为了快速有效地筛选潜在匹配,本文采用实体的最小外包矩形(MBR)来代替实体进行运算。MBR是包含实体最小x-y的平行矩形,具有简单、高效的特点,它是地理实体使用最广泛的近似表达[26]。这样就可以将要素聚合搜索转化为MBR组合的搜索,搜索组合数从2n减少为n4。此外,本文还引入回溯法来提高MBR组合搜索的效率。回溯法是一种常用的组合搜索算法,其优势在于能适时“回头”,若再往前搜索不到解,就退回一步重新选择,可以大大提高搜索效率。回溯法最典型的应用是解决N皇后问题[27]。算法设计如下:
设目标组合MBR的宽和高分别w和h,ε为算法搜索阈值,问题的解向量O={o1,o2,o3,o4},共n4个状态,当前解状态为*。若o1=o2=o3=o4,则目标候选实体只有一个要素,否则为多个要素聚合。由于MBR组合优化搜索时,解向量中已存在的元素会影响解向量中其他元素的搜索,所以搜索解空间不同层次结点时约束函数不同。为了快速回溯,本文还在定义解空间树时,对结点进行了排序。算法涉及的约束函数包括

(1)
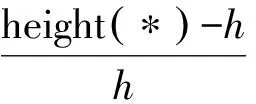
(2)
ymin(o3)≤ymin(*)
(3)
ymax(o4)≤ymax(*)
(4)

(5)
最优解s计算公式为
(6)
算法解题步骤如下:
(1) 实体排序。沿x正逆方向和y正逆方向按照MBR的xmin、xmax、ymin和ymax对b中要素排序,结果分别为Oxmin、Oxmax、Oymin和Oymax。
(2) 建立深度为5的完全n叉解空间树。根结点为o,o派生出n个子结点,o的子结点再派生出n个子结点,以此类推,整个解空间树为一棵n叉的满树,包含n4+1个结点。为了进一步提高搜索效率,子结点按照一定顺序排列,第2层按照Oxmin排列,第3层按照Oxmax排列,第4层按照Oymin列,第5层按照Oymax建立的解空间树。
(3) 约束函数。第3层约束函数为式(1)和式(2),第4层为式(1)、式(2)和式(3),第5层为式(1)、式(4)和式(5)。
(4) 初始化。当前O为null,当前解的最优值s为0。
(5) 搜索。按照深度优先策略,从根结点出发搜索树,搜索到第2层时,记录解为{o1,null,null,null},搜索到第3层结点时,判断该结点是否满足约束函数,若不满足约束函数,则跳过对该结点为根的子树的搜索,且与该结点同一层,排序小于该结点其他结点也不用搜索,回溯至上一层,此时解为{};否则,记录解为{o1,o2,null,null}对以该结点为根的n棵子树,继续按照深度优先策略进行搜索,操作步骤与上述一致。
(6) 最终获得所有解向量,根据式(6)计算最优值s,按照s对解集排序。
完成相似MBR查询后,对齐MBR的几何中心点,然后通过面积重叠排除无关要素。本文以图2中数据演示算法查询过程,搜索阈值ε=0.2,MBR在xmin上排序已显示,如图2(a)所示。
第1步:实体排序,Oxmin={b1,b2,b4,b3,b5,b6}、Oxmax={b5,b6,b4,b3,b2,b1}、Oymin={b3,b6,b2,b4,b5,b1}、Oymax={b5,b1,b2,b4,b3,b6}。
第2步:建立深度为5的完全六叉解空间树,如图2(b)所示。由于篇幅有限,本文仅列出每一层中一个子树的排列情况。
第3步:初始化,当前O为null,当前解的最优值s为0。

第5步:搜索第2层b2子树,{b2,b5,null,null}和{b2,b6,null,null}不满足约束函数,进行剪枝;{b2,b4,null,null}满足约束函数,进入下一层搜索,{b2,b4,b3,null}满足约束函数,进入下一层{b2,b4,b3,b2}满足约束函数,为可行解;{b2,b4,b2,null}满足约束函数,进入下一层,{b2,b4,b2,b2}满足约束函数,为可行解。以此类推,最终获得所有可行解为O1={b2,b4,b2,b2}、O2={b4,b6,b6,b4}、O3={b2,b4,b3,b2}和O4={b4,b5,b4,b5}。
第6步:将a的MBR对齐可行解MBR,通过面积重叠筛选无关要素。获取a的候选匹配分别为{b2,b4}和{b4,b5}。
基于回溯的MBR组合优化算法最坏的情形可搜索到n4种情况。但在实际搜索中,如图2中数据演示一样,回溯法所产生的结点数通常只有解空间树结点数的一小部分,所以应用回溯法有效提升了搜索效率。
1.2 空间域划分
MBR组合优化算法实现了单向的要素聚合搜索,即输入数据A中实体a,能在数据B中查询到a的候选匹配。然而,对于多对多匹配候选,需要一并获得A和B中对应的聚合要素集,即实现双向搜索。本文的策略是首先在数据A(或B)中搜索聚合要素集,然后输入初次搜索到的聚合要素集,在B(或A)中搜索其候选匹配。但直接在A(或B)中搜索聚合要素集,将导致搜索到的聚合要素集数爆炸,且获取的大多数聚合要素集是无效的。为此本文提出空间域的概念,目的是将实体划分到一个个闭合的空间区域内。这些闭合的空间区域没有分隔应聚合的要素集,本文定义其为空间域。它包含两个重要特征:一是边界性,划定了MBR组合优化算法的搜索范围,避免了搜索结果爆炸的困境;二是连续性,保证了聚合要素集的整体性没有被破坏。
在地理空间分布模式中,Gestalt原则得到广泛认同,并用于指导地图综合[28]。Gestalt原则认为一群地理要素根据视觉感受进行分组时,将结构模式一致性且邻接的要素集放在一起。例如,在地图综合时,会将存在邻接关系且具有一定特征相似性的要素进行综合。对于多对多匹配中聚合要素集,其要素之间应存在邻接关系,类似于“飞地”现象是极少存在的。本文依据Gestalt原则来划分多对多匹配的空间域。首先,将匹配实体分为两类,设A0={a1,a2,…,am}和B0={b1,b2,…,bm}分别为A和B的第1类实体,A1={am+1,am+2,…,am+p}和B1={bn+1,bn+2,…,bn+q}分别为A和B中的第2类实体;然后,使用Delaunay三角网构建邻接第1类实体中A0或B0的邻接关系[29],具体操作为获取A0中要素的几何中心点VA0={v(a1),v(a2),…,v(am)},通过VA0创建Delaunay三角网。最后将压盖了A1中实体的三角空间进行合并,这些单个的三角空间区域或多个三角空间合并的区域即为A1的空间域。在划分操作中,A0和B0不包含M∶N匹配类型,通过A0建立Delaunay三角网后,M∶N匹配就分布在一个或多个三角空间内,然后合并压盖A1中实体的三角空间,避免了M∶N匹配中A1来源的聚合要素集被破坏,因此保证了空间域的边界性和连续性。如图3所示,第1类实体的Delaunay邻接关系已构建,D1、D2、D3和D4为形成的三角区域,D1、D2和D3与A1中要素相交,则将他们记录为合并;D3和D4也与A1中要素相交,则将D3和D4记录为合并;最后将D1、D2、D3和D4进行合并,形成一个空间域,即为图中阴影区域。
空间域获取后,通过MBR组合优化算法在空间域内查找A1中聚合要素集,此时聚合条件为目标MBR至少包含两个面要素,然后输入初次查询到的聚合要素集,再次利用MBR组合优化算法在B1中搜索其候选匹配。
1.3 基于ANN的多因子面实体评价方法
获得候选匹配后,一个匹配评价方法被用于评估被调查候选匹配是否为几何上的正确匹配。匹配评价是一个复杂的决策过程,包含了特征因子的选定和根据这些因子做出决策两部分。本文选取的面实体特征因子包括距离、大小、方向和形状。同时,为了避免人为设置决策模型的权重和阈值,本文通过机器学习算法——人工神经网络的学习确定决策模型的权重和阈值。人工神经网络(ANN)广泛应用于科学和工程问题,它试图模拟生物神经系统的识别模式[30]。在实体匹配中,如果不同地图中两个实体的多个特征存在相似性,则它们可能是同名实体,本文将该判断过程拟合为一个人工神经网络的模式识别过程。本文采用ANN中3层BPNN来解决该问题。BPNN是一种误差反向传播的前馈学习算法,其对希望的映射能达到全局最优逼近,且具有较强的泛化能力[31]。BPNN包含输入层(input layer)、隐含层(hidden layer)和输出层(output layer)。本文选择输入层为特征因子中的距离(Sdis)、大小(Ssize)、方向(Sdir)和形状(Sshape)相似度,隐含层设置为9个节点,输出层为1(匹配)和0(不匹配)。BPNN输出匹配结果时,同时能得到该实体对匹配(归为1)的概率P,不匹配概率为1-P。当P≥0.5时,则实体对匹配,且P越接近1,实体对越相似;反之P<0.5,1-P越接近1,实体越不相似。各特征因子计算公式如下:
(1) 距离相似度,采用文献[32]提出的距离相似度计算公式
(7)
式中,ra、rb分别为面实体a和b最小外接矩形对角线长的一半,d(a,b)表示a、b之间的几何中心点之间的距离,其计算公式为
(8)
几何中心点计算公式为
(9)
(2) 大小相似度
(10)
(3) 方向相似度
(11)
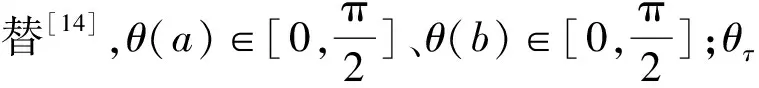
(4) 形状相似度。本文采用转角函数法[22]来描述面实体的形状。转角函数法是基于轮廓的形状描述方法,被广泛应用的闭合折线形状描述[33]。如图4所示,a和b面实体从P0点沿顺时针方向展开,记录每一段弧的长度,以归一化长度作为X轴,沿弧每点的转向角累加值作为Y值。转角函数形状相似性计算公式为
(12)
式中,θa(x)和θb(x)分别是面实体a、b转向角累加值。
为了适应于一对多和多对多匹配特征因子的相似性计算,本文采用凸包将聚合要素集联合为单一面实体进行评价。
2 匹配流程
整个匹配流程主要有5个组成部分:①数据预处理,主要包括格式转换、拓扑检查、几何坐标转换,目的是解决不同来源数据的系统性错误[34];②训练决策模型,随机选择样本,计算每个样本数据的距离、大小、方向和形状特征的相似度,并人工匹配样本数据,输入特征数据和匹配结果数据训练神经网络,并采用测试样本测试所训练模式;③初匹配,利用MBR组合优化算法获取1∶1和1∶N的候选匹配,然后通过已训练的决策模型评估这些候选匹配;④基于初匹配结果将已匹配的实体标记A0和B0,未匹配的实体标记为A1和B1,主要包含M∶N匹配和1∶0匹配。通过A0创建Delaunay三角网,划分多对多匹配空间域;⑤在空间域内查询A1的聚合要素集,然后通过该聚合要素集在B1查找其候选匹配,最后通过已训练的决策模型评估这些候选匹配,获取所有匹配结果。
3 试验与分析
3.1 试验数据
本文选取浙江省舟山市1∶2000岛礁海洋基础空间要素数据居民地与设施面(数据A)和1∶10 000临海区域陆地基础空间要素数据居民地与设施面(数据B)进行匹配算法的验证,数据A和数据B叠加在一起的情况如图5所示。
图5(a)为全部数据叠加在一起显示,图5(b)、5(c)和5(d)为图5(a)中部分区域的放大显示,其中图5(b)是居民建筑物面,图5(c)是工业设施面,图5(d)是露天采掘场面。大面实体相对位置偏差较少,如图5(d)所示,但是小面实体相对位置偏差较大,如图5(b)所示。试验数据的统计信息如表1所示。

表1 试验数据详细信息
本文算法通过Microsoft Visual Studio 2010(C#)+ ArcGIS Engine10.1实现,并通过Spyder+Python3.5构建BP神经网络评价模型及预测匹配结果。本试验在core i5 CPU 2.6Hz Win8操作系统上运行。
3.2 训练决策模型
试验选取了数据B中大约20%的实体所产生的964个候选匹配作为样本来训练BP神经网络模型,样本匹配结果是人工确认的。样本中包含86个1∶1匹配样本,正确匹配52个,错误匹配34个;849个1∶N匹配样本,正确匹配375个,错误匹配474个;29个M∶N匹配样本,正确匹配11个,错误匹配18个。样本数据中一半作为训练数据,另一半作为测试数据。按照2.3节模型设定,本文所选取的BP神经网络模型隐含层节点数为9个,激活函数为logistic函数,学习效率设为0.01,动量因子设为0.9,最大迭代次数为1000次。最终,所训练的模型匹配测试数据,精度为89%。
3.3 试验对比与分析
3.3.1 试验对比
为定量评价所提出匹配方法的性能,本文通过与人工检查的结果进行比较来评估匹配结果,评价公式采用最流行F1-Measure,其计算公式为
(13)
式中,P为准确率;R为召回率;TP为正确匹配数;FP为错误匹配数;AM为人工无法判断的匹配数;FN为漏匹配数。试验中设置本文方法缓冲分析距离σ=30 m,MBR组合优化算法搜索阈值ε=0.2。为了验证本文算法对坐标偏移情况的解决能力,选取文献[18]方法进行对比。文献[18]方法首先利用面积重叠法(重叠率S≥0.5)正向获取候选匹配,然后通过距离、大小、方向和长度构建BPNN评价模型筛选正确匹配;再通过面积重叠法反向获取未匹配实体的候选匹配,然后再利用已构建的BPNN评价模型筛选正确匹配。为方便表示,本文方法简记为MBRCO-ANN(minimum bounding rectangle combinatorial optimization algorithm & artificial neural network),对比方法为BAO-ANN(bidirectional area overlap & artificial neural network)。BAO-ANN方法仍然采用上文介绍的样本数据进行训练,两种方法匹配结果统计如表2所示。

表2 两种方法的匹配结果统计
从表2中可看出,本文MBRCO-ANN方法的准确率、召回率均高于对比的BAO-ANN方法,因此整体表现(F1)也优于BAO-ANN方法,但BAO-ANN方法耗时远小于本文方法。此外,两种方法都取得了相对较高的准确度,说明基于人工神经网络的决策模型在实体匹配领域也有良好表现。本文方法精度略高于BAO-ANN方法,这主要是因为:①本文中选取的正切空间函数法来描述形状特征相较于BO-ANN的实体长度信息更精确;②本文中MBR组合优化算法可获得相对较多的候选匹配,这有利于从多个候选中选择出最佳匹配。
两种方法获得候选匹配对比如图6、图7和图8所示。图中N为获得候选匹配的总数,Ncontain为所获得的候选匹配中包含的正确匹配数,Pcontain为包含率,其计算公式为
(14)
从图6可知,MBRCO-ANN方法获得了7584个候选匹配,远多于BAO-ANN方法获得的793个候选匹配。由于大量的候选匹配需要计算位置、大小、方向和形状的相似度,因此本文方法较BAO-ANN方法耗时多。但是获取的大量候选匹配也减少了正确匹配的漏选,如图7和图8所示,MBRCO-ANN方法获得了740个有效候选匹配,包含率达到了95.1%,而对比的BAO-ANN方法仅获得了449个有效候选匹配,包含率为57.7%。这也直接限制了BAO-ANN方法召回率的提升。因此本文MBRCO算法获得候选匹配的能力显著高于BAO-ANN方法中的面积重叠方法。
图9和图10展示了两种方法在位置偏移较大情况下的细节表现。图9显示该区域匹配数据存在较大位置偏差,同名实体面积重叠效果较差。表3显示MBRCO-ANN方法获得了7对正确匹配,0对错误匹配和3对漏匹配,而BAO-ANN方法获得了3对正确匹配,1对错误匹配和7对漏匹配。MBRCO-ANN方法未检测到的3对匹配:b376∶a263、b375∶a273和b271∶a377,其中存在明显的形状差异,如图9(a)所示,所以MBR组合优化算法未检测到。BAO-ANN方法中的错误匹配对:a238∶b382,这是由于b382通过面积重叠法只找到了a238,且a238与b382的预测的相似度为0.972,因此造成错误匹配。而本文MBRCO-ANN方法可同时检测到a238:b382和a238,a240:b382,其预测的相似度分别为0.885和0.917,因此本文方法可以选择出最佳匹配a238,a240:b382。此外BAO-ANN方法基于面积重叠率S≥0.5漏选了7对正确匹配,即使通过调整重叠率S,a259:b397a260,a262:b769,b770和a259:b375依然会漏选。同时还需注意的是,调整重叠率S还可能造成过度识别,如:a262和b379。因此,直接的面积重叠法是不能解决位置偏移情况下候选匹配的有效识别问题的。
表3两种方法在图9中数据匹配情况统计
Tab.3MatchingresultsofMBRCO-ANNandBAO-ANNmethodinexample1

方法正确匹配对错误匹配对漏匹配对MBRCO-ANNa233,a240∶b331a253∶b499a254∶b381a259∶b397a260,a262∶b769,b770a261∶b378a265∶b615a274∶b766b376b377b375BAO-ANNa253∶b499a261∶b378a265∶b615a238∶b382b381b397b769,b770b376b377b375b765
从表4可知,MBRCO-ANN方法识别了全部的匹配,包括2对1∶N匹配和3对M∶N匹配,而BAO-ANN方法只获得了5对正确匹配,但存在2对错误匹配,1对漏匹配。从图10(b)可看出,BAO-ANN方法错误压盖了一些面积很小的实体(a4955和a5236),或者忽略了一些实体(如a5327和a6170),造成错误匹配(a4955,a5167,a5760,a5806,a5842,a6175∶b767,b768和a5236,a5975,a6173,a6174a6180,a6195∶b354)。这种错误(或过度)压盖在1∶N和M∶N匹配类型中经常出现,即使通过精确决策模式也不能解决这些微小的差异。因此本文提出的不依赖于位置精确的MBRCO-ANN方法在解决1∶N和M∶N匹配中具有明显的优势。
表4两种方法在图9中数据匹配情况统计
Tab.4MatchingresultsofMBRCO-ANNandBAO-ANNmethodinexample2
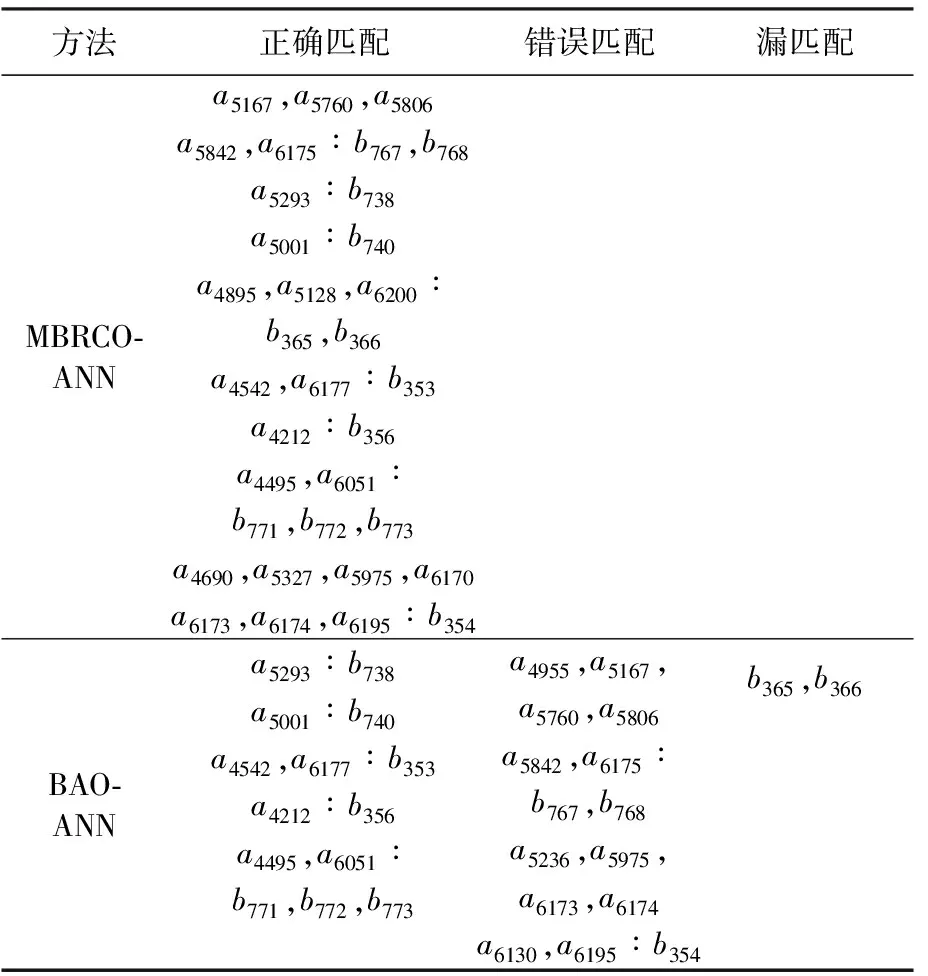
方法正确匹配错误匹配漏匹配MBRCO-ANNa5167,a5760,a5806a5842,a6175∶b767,b768a5293∶b738a5001∶b740a4895,a5128,a6200∶b365,b366a4542,a6177∶b353a4212∶b356a4495,a6051∶b771,b772,b773a4690,a5327,a5975,a6170a6173,a6174,a6195∶b354BAO-ANNa5293∶b738a5001∶b740a4542,a6177∶b353a4212∶b356a4495,a6051∶b771,b772,b773a4955,a5167,a5760,a5806a5842,a6175∶b767,b768a5236,a5975,a6173,a6174a6130,a6195∶b354b365,b366
3.3.2 参数分析
由于神经网络减少了参数的人为设定,但是本文方法也使用了缓冲区距离σ和MBR组合优化算法阈值ε。σ的值由匹配数据中同名实体最大偏移距离决定,σ过小,部分偏移较大的同名实体不能被选中;σ设置为太大值时,会获得更多的候选匹配,但也增加程序运算时间。本文试验中,σ根据多次试验选择为30 m。不同参数ε(0.05,0.1,0.2,0.3,0.4)对本文所提出的MBR组合优化算法表现的影响,如图11所示。
从图11中可知,当ε过小时,一些正确的匹配候选没有被MBR组合优化算法查询到,因此召回率很低,相应也影响了整体表现(F1)。当ε逐渐增大至0.2时,召回率急剧上升,准确率和F1值也相应上升,这是由于更多的候选匹配让正确匹配被发现。当ε继续增大时,准确率和召回率相对平稳,这是由于ε在0.2左右时,绝大多数正确匹配已经被搜索到。匹配耗时是随着ε增大,先相对平稳后急剧上升,这是由于ε过小时初次匹配中很多候选匹配没有获取到,但未查询到的匹配对增加了二次匹配的检索负担。当ε逐渐增大至0.2时,初次匹配中越来越多正确匹配搜索到,二次匹配检索工作减少,匹配耗时相对稳定;当ε继续增大时,大量无效候选匹配被搜索到,匹配耗时急剧增加。所以ε的取值从1.8到2.5之间,本文方法在精确度和耗时方面达到较好均衡。

图1 位置偏移的匹配数据Fig.1 Matching data in positional discrepancy
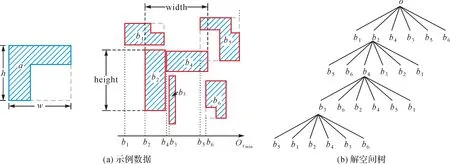
图2 MBR组合优化算法示意图Fig.2 MBR combinatorial optimization algorithm

图3 三角空间合并示意图Fig.3 Merging triangular spaces
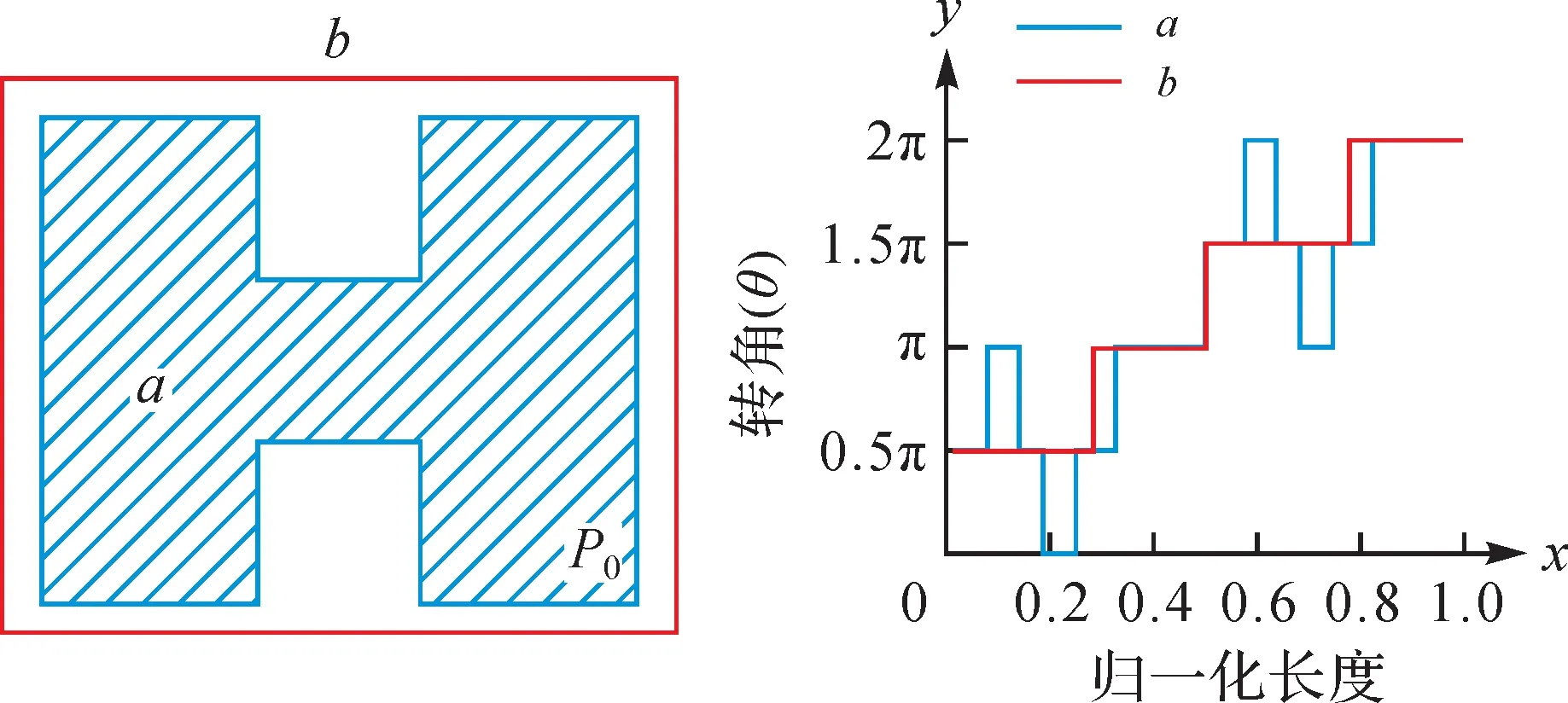
图4 面a和b转角函数形状描述图Fig.4 Shape description of polygon a and b by the turning function
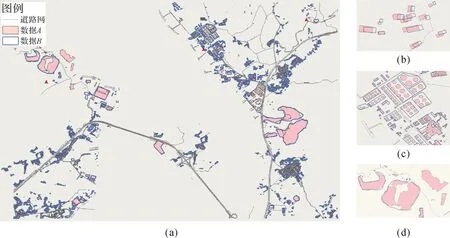
图5 试验数据Fig.5 Test data
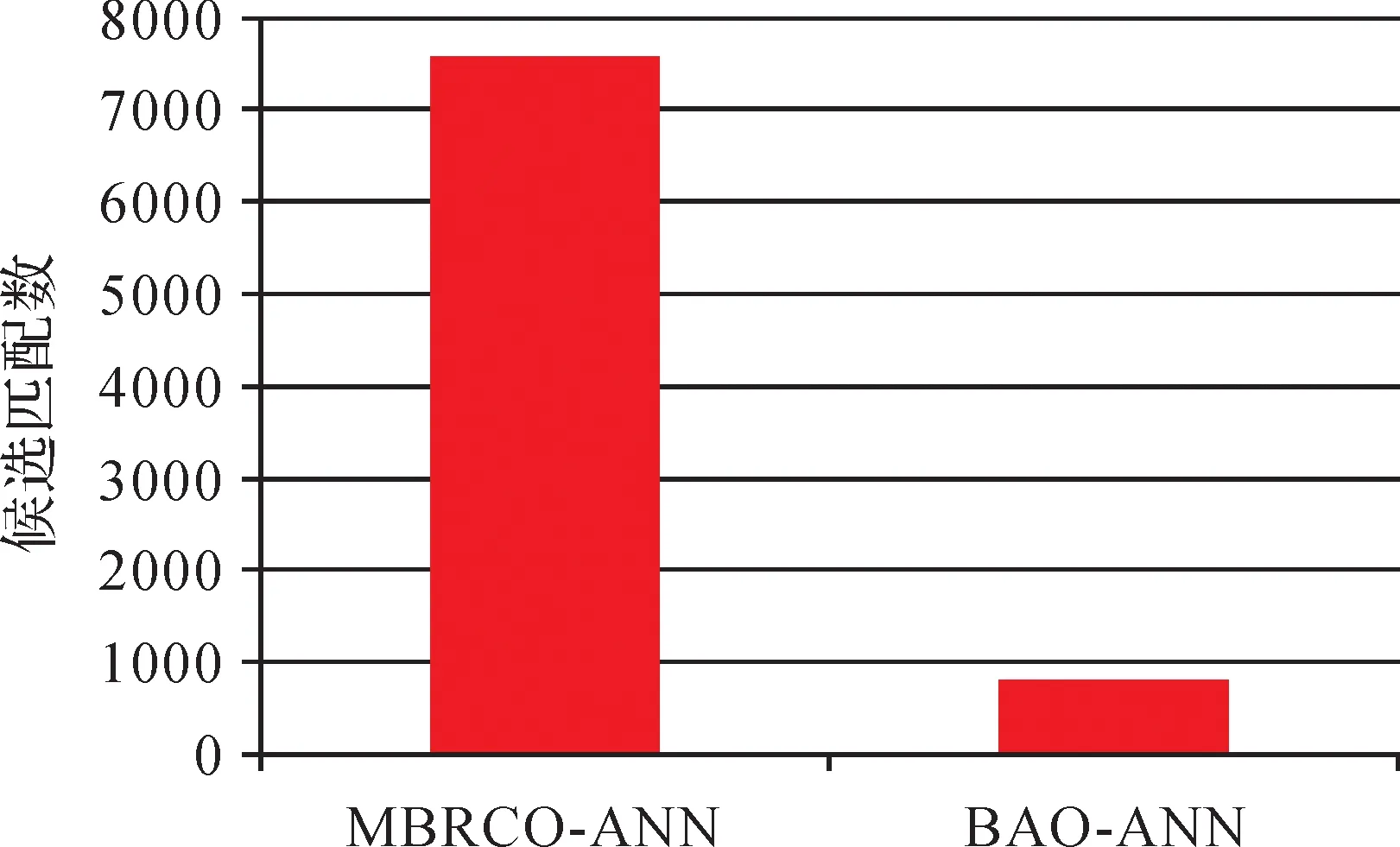
图6 候选匹配总数Fig.6 Number of identifying the potential matching pairs

图7 有效候选匹配数Fig.7 Number of identifying the effective potential matching pairs
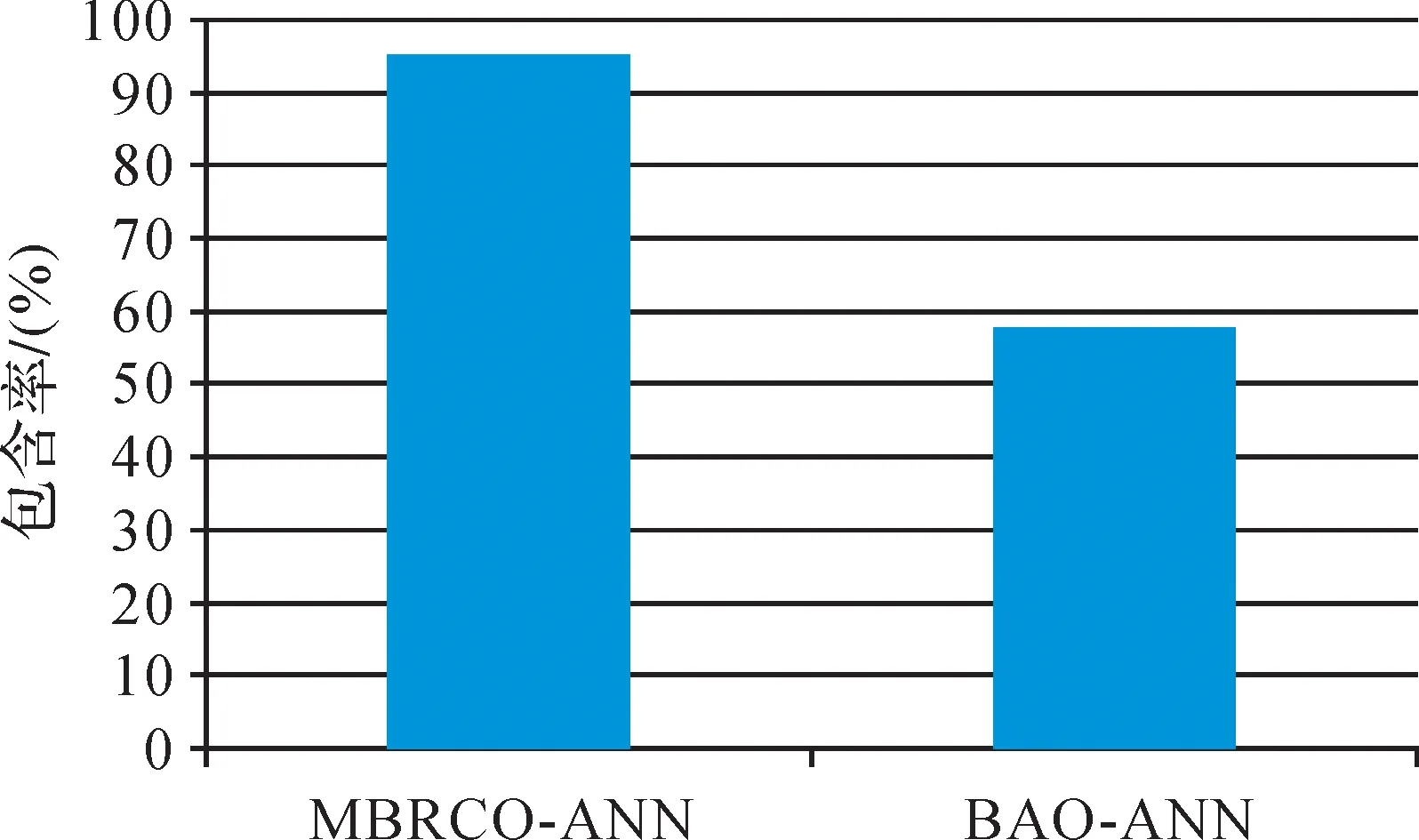
图8 包含率Fig.8 Percentage of containing
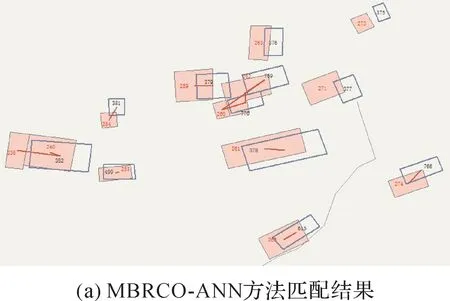

图9 示例1:使用MBRCO-ANN方法和BAO-ANN方法获得的匹配结果Fig.9 Matching results of example 1 according to MBRCO-ANN and BAO-ANN methods
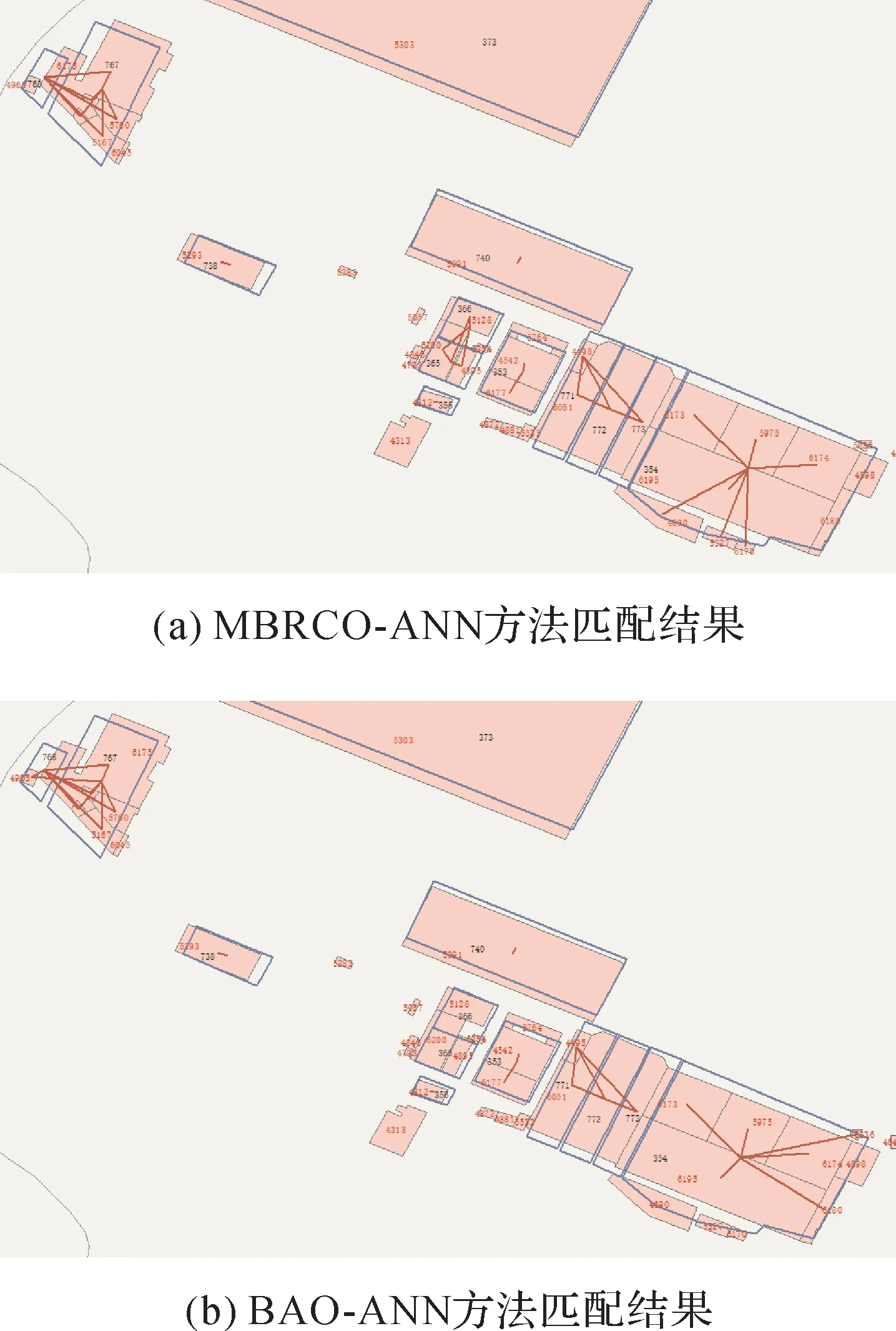
图10 示例2:使用MBRCO-ANN方法和BAO-ANN方法获得的匹配结果Fig.10 Matching results of example 2 according to MBRCO-ANN and BAO-ANN methods
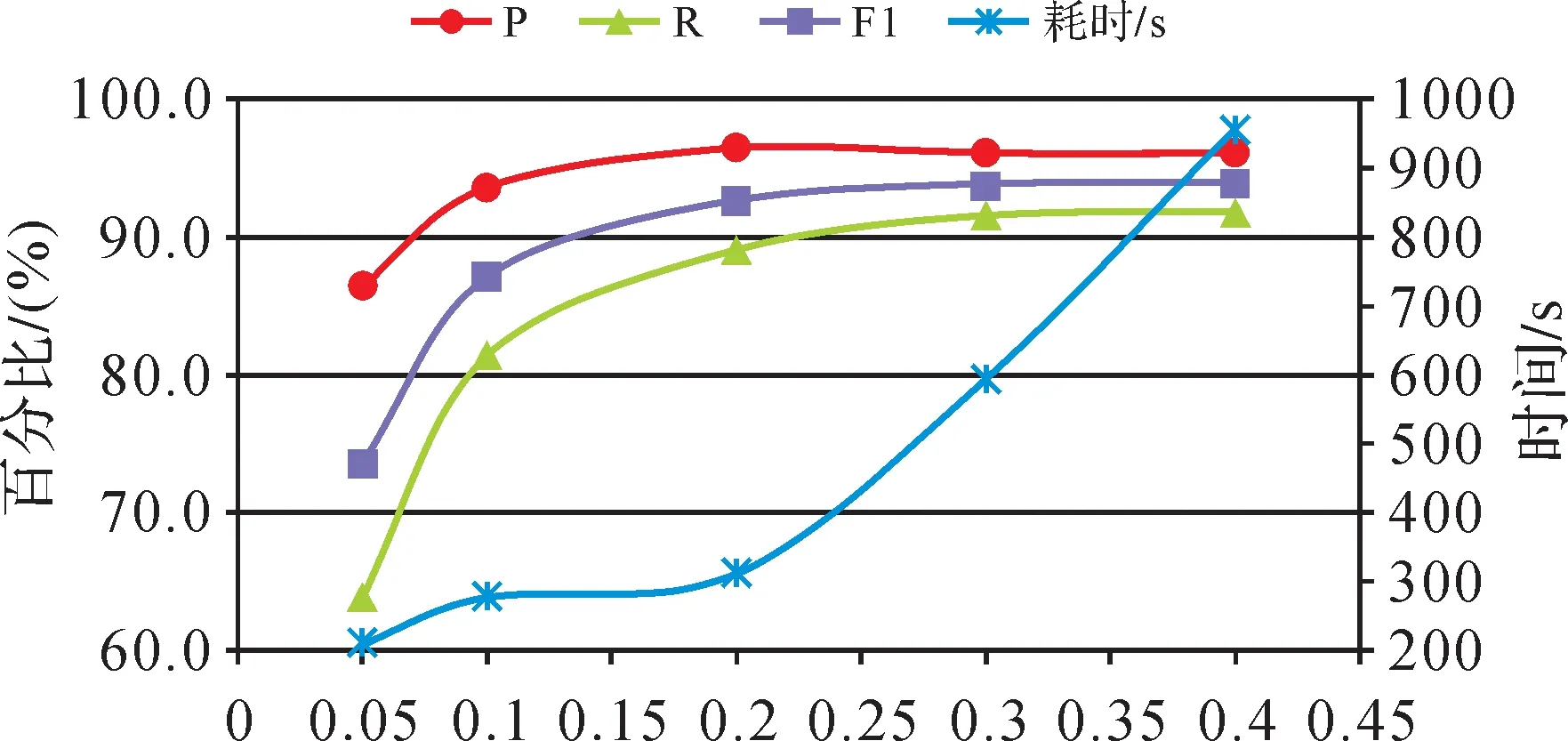
图11 不同ε下准确度、召回率、F1和耗时变化 Fig.11 Precision, recall, F1 and computer time with different value of ε
4 结 论
本文提出了基于MBR组合优化算法的多尺度面实体匹配方法,该方法包含3个部分:①MBR组合优化算法,其解决了单向(1∶1和1∶N)候选匹配搜索问题;②基于空间域改进MBR组合优化算法,通过划分空间域限定了查询算法的搜索范围,以解决双向(M∶N)候选匹配的搜索问题;③构建基于距离、大小、方向和形状的人工神经网络匹配评价模型来识别几何上相似的匹配对。本文所提出的方法试验于存在位置偏差的不同尺度面数据,结果表明,本文方法能够有效克服位置偏差对匹配的影响。下一步工作将侧重于改进获得候选匹配的效率,并且将该方法扩展到道路网的匹配。
参考文献:
[1] LI Linna, GOODCHILD M F. Automatically and Accurately Matching Objects in Geospatial Datasets[M]∥GOODCHILD M F, LEUNG Y, SHI Wenzhong, et al. Advances in Geo-Spatial Information Science. London, UK: CRC Press, 2012: 71-79.
[2] SAALFELD A. Automated Map Conflation[D]. Washington DC: University of Maryland, 1993: 1-10.
[3] RUIZ J J, ARIZA F J, UREA M A, et al. Digital Map Conflation: A Review of the Process and a Proposal for Classification[J]. International Journal of Geographical Information Science, 2011, 25(9): 1439-1466.
[4] GIRRES J F, TOUYA G. Quality Assessment of the French OpenStreetMap Dataset[J]. Transactions in GIS, 2010, 14(4): 435-459.
[5] YANG Bisheng, ZHANG Yunfei, LUAN Xuechen. A Probabilistic Relaxation Approach for Matching Road Networks[J]. International Journal of Geographical Information Science, 2013, 27(2): 319-338.
[6] DEVOGELE T, PARENT C, SPACCAPIETRA S. On Spatial Database Integration[J]. International Journal of Geographical Information Science, 1998, 12(4): 335-352.
[7] WALTER V, FRITSCH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5): 445-473.
[8] GOODCHILD M F. Chapter Four-attribute Accuracy[M]∥GUPTILL S C, MORRISON J L. Elements of Spatial Data Quality: A Volume in International Cartographic Association. Amsterdam: Elsevier, 1995: 59-79.
[9] GUPTILL S C, MORRISON J L. Elements of Spatial Data Quality[M]. Oxford, UK: Elsevier Science, 1995.
[10] ZHANG Xiang, AI Tinghua, STOTER J, et al. Data Matching of Building Polygons at Multiple Map Scales Improved by Contextual Information and Relaxation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 92(2): 147-163.
[11] DEVOGELE T, TREVISAN J, RAYNAL L. Building a Multi-scale Database with Scale-transition Relationships[C]∥Proceedings of the 7th International Symposium on Spatial Data Handling. Delft, The Netherlands: SDH, 337-351.
[12] SAMAL A, SETH S, CUETO K, et al. A Feature-based Approach to Conflation of Geospatial Sources[J]. International Journal of Geographical Information Science, 2004, 18(5): 459-489.
[13] KIM J O, YU K, HEO J, et al. A New Method for Matching Objects in Two Different Geospatial Datasets Based on the Geographic Context[J]. Computers & Geosciences, 2010, 36(9): 1115-1122.
[14] XAVIER E M A, ARIZA-LPEZ F J, UREA-CMARA M A. A Survey of Measures and Methods for Matching Geospatial Vector Datasets[J]. ACM Computing Surveys, 2016, 49(2): 39.
[15] ZHANG X, ZHAO X, MOLENAAR M, et al. Pattern Classification Approaches to Matching Building Polygons at Multiple Scales[C]∥ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Melbourne: ISPRS, 2012: 19-24.
[16] 郭泰圣, 张新长, 梁志宇. 神经网络决策树的矢量数据变化信息快速识别方法[J]. 测绘学报, 2013, 42(6): 937-944.
GUO Taisheng, ZHANG Xinchang, LIANG Zhiyu. Research on Change Information Recognition Method of Vector Data Based on Neural Network Decision Tree[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 937-944.
[17] 付仲良, 杨元维, 高贤君, 等. 道路网多特征匹配优化算法[J]. 测绘学报, 2016, 45(5): 608-615. DOI: 10.11947/j.agcs.2016.20150388.
FU Zhongliang, YANG Yuanwei, GAO Xianjun, et al. An Optimization Algorithm for Multi-characteristics Road Network Matching[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 608-615. DOI: 10.11947/j.agcs.2016.20150388.
[18] WANG Yanxia, CHEN Deng, ZHAO Zhiyuan, et al. A Back-propagation Neural Network-based Approach for Multi-represented Feature Matching in Update Propagation[J]. Transactions in GIS, 2015, 19(6): 964-993.
[19] FU Zhongliang, WU Jianhua. Entity Matching in Vector Spatial Data[C]∥International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: ISPRS, 2008, 37(5): 1467-1472.
[20] VON GOESSELN G, SESTER M. Change Detection and Integration of Topographic Updates from ATKIS to Geoscientific Data Sets[C]∥Proceedings of International Conference on Next Generation Geospatial Information. Boston: International Conference on Next Generation Geospatial Information, 2003.
[21] HUH Y, KIM J, LEE J, et al. Identification of Multi-scale Corresponding Object-set Pairs between Two Polygon Datasets with Hierarchical Co-clustering[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 88(1): 60-68.
[22] ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al. An efficiently Computable Metric for Comparing Polygonal Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(3): 209-216.
[23] XU Yongyang, XIE Zhong, CHEN Zhanlong, et al. Shape Similarity Measurement Model for Holed Polygons Based on Position Graphs and Fourier Descriptors[J]. International Journal of Geographical Information Science, 2017, 31(2): 253-279.
[24] 许俊奎, 武芳, 朱健东, 等. 相邻比例尺居民地匹配[J]. 武汉大学学报(信息科学版), 2014, 39(3): 340-345.
XU Junkui, WU Fang, ZHU Jiandong, et al. A Multi-to-Multi Matching Algorithm between Neighborhood Scale Settlement Data[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 340-345.
[25] ZHANG Meng, MENG Liqiu. An Iterative Road-matching Approach for the Integration of Postal Data[J]. Computers, Environment and Urban Systems, 2007, 31(5): 597-615.
[26] COBB M A, PETRY F E, SHAW K B. Fuzzy Spatial Relationship Refinements based on Minimum Bounding Rectangle Variations[J]. Fuzzy Sets and Systems, 2000, 113(1): 111-120.
[27] KNUTH D E. The Art of Computer Programming[M]. Upper Saddle River, NJ: Addison-Wesley, 1968.
[28] LI Z, YAN H, AI T, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory[J]. International Journal of Geographical Information Science, 2004, 18(5): 513-534.
[29] TSAI V J D. Delaunay Triangulations in TIN Creation: An Overview and a Linear-time Algorithm[J]. International Journal of Geographical Information Systems, 1993, 7(6): 501-524.
[30] CRACKNELL M J, READING A M. Geological Mapping Using Remote Sensing Data: A Comparison of Five Machine Learning Algorithms, Their Response to Variations in the Spatial Distribution of Training Data and the Use of Explicit Spatial Information[J]. Computers & Geosciences, 2014, 63(1): 22-33.
[31] FUNAHASHI K I. On the Approximate Realization of Continuous Mappings by Neural Networks[J]. Neural Networks, 1989, 2(3): 183-192.
[32] 汪汇兵, 唐新明, 邱博, 等. 运用多算子加权的面要素几何匹配方法[J]. 武汉大学学报(信息科学版), 2013, 38(10): 1243-1247.
WANG Huibing, TANG Xinming, QIU Bo, et al. Geometric Matching Method of Area Feature Based on Multi-weighted Operators[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1243-1247.
[33] FAN Hongchao, ZIPF A, FU Qing, et al. Quality Assessment for Building Footprints Data on OpenStreetMap[J]. International Journal of Geographical Information Science, 2014, 28(4): 700-719.
[34] DOYTSHER Y. A Rubber Sheeting Algorithm for Non-Rectangular Maps[J]. Computers & Geosciences, 2000, 26(9-10): 1001-1010.

