舰载主炮武器系统在航阶段技术状态效能评估

郭 柳,顾雪峰,刘旺锁

(海军工程大学, 武汉 430033)

现代海战中，主炮作为水面舰艇的重要作战力量之一，其系统技术状态效能的发挥与战争结果息息相关。现阶段，人们通过计算机模拟和收集各种海上实验数据，建立舰载主炮武器系统技术状态效能综合评判模型，得出效能评估值。但在建模过程中发现，由于受系统各有关因素的影响，对模拟的准确性存在一定的误差。在建成模型中这些影响因素均有相当程度的模糊性和不确定性，导致它们所产生的影响没有一个明确的等级界限。因此，用模糊数学的方法[1-4]对舰载主炮武器系统技术状态的效能进行综合评估，以弥补模拟及试验方法的不足。

1 舰载主炮武器系统在航阶段技术状态效能评估分析方法

1.1 层次分析法

层次分析法(Analytic Hierarchy Process,AHP)是美国运筹学家T.L.Satty教授于20世纪70年代提出的一种简便、灵活而又实用的系统分析方法[5-7]，其主要步骤如图1所示。

1) 建立层次结构模型

2) 构造判断矩阵

关于判断矩阵的值，基于心理学研究，T.L.Satty等人建议引用数字1～9及其倒数作为标度，其含义如表1。

表1 判断矩阵中值的含义

3) 层次单排序

层次单排序可以归结为计算判断矩阵的特征根和特征向量，并根据式(1)检验其一致性

(1)

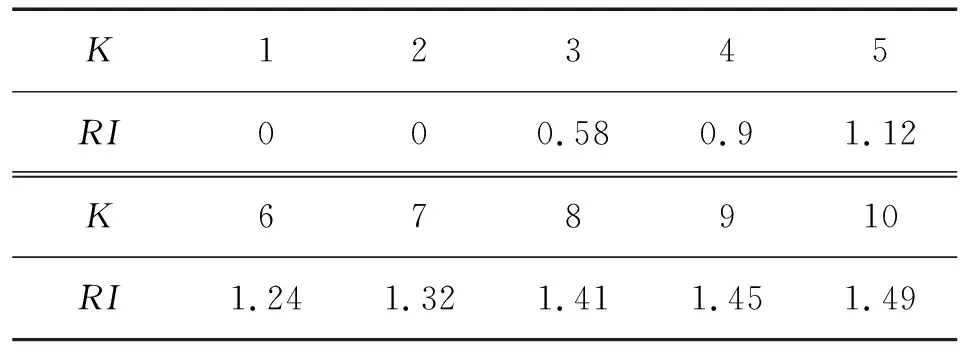
当判断矩阵具有完全一致性时，CI=0。λmax x-k越大，CI越大，矩阵的一致性越差，就需要对判断矩阵进行调整。同时为了检验矩阵是否具有满意的一致性，需要将CI与平均随机一致性指标RI进行比较。

4) 层次总排序

利用同一层次中所有层次单排序的结果，计算本层次所有因素重要性的权值。

5) 一致性检验

与单排序类似的一致性指标检验。

6) 最后，根据专家评判各元素的满意度用式(2)来进行效能值的运算

(2)

1.2 模糊综合评判方法

模糊综合评判利用模糊数学中的隶属度概念量化人对对象系统中各要素感觉“好”与“不好”的程度，然后在对对象的各个主要因素进行重要性判断的基础上，给出各个因素的权重，运用模糊运算模型得到综合评价结果[8-10]，其步骤如下：

1) 建立舰载武器系统技术状态评估体系。

2) 确定评价因素集，U={u1,u2,…,um}。

3) 确定评价等级，将评语组成评语集V，在本文中，评语集为差，中，良，优。

4) 对武器系统评价因素集U中的单因素ui(i=1,2,…,m)作模糊评价，确定因素ui对应的评价等级vi(i=1,2,…,n)的隶属度rij。

5) 明确各类评价因素的相对权重向量

W=[w1,w2,w3,…,wi]

6) 计算综合评价向量

在求得因素集中诸因素相应的模糊判断矩阵R=(rij)m×n以及因素集的权向量W=[w1,w2,w3,…,wi]后，根据模糊集理论中的综合计算方法，得出模糊综合评价的评价向量。

2 案例分析

2.1 应用AHP法进行技术状态效能评估

1) 通过分析舰载主炮武器系统的结构组成和作战中的应用情况，以主炮系统各组成部分中的主要构成分系统为例建立主炮武器系统技术状态效能评估指标体系。如图2所示。

2) 根据其层次结构模型，构造判断矩阵。对矩阵因素层各因素的重要性进行两两对比，并参照表1进行取值。同时，计算出最大特征根，并做一致性判断。如表3～表5所示。

AB1B2B3B4PB112430.46B21/21320.31B31/41/311/20.1B41/31/2110.13λmax=3.875<4.27

表4 第二层矩阵B1指标权重值

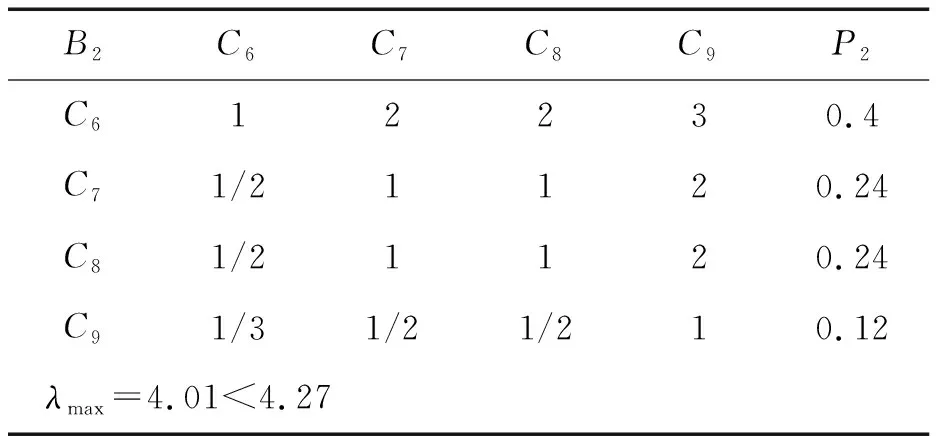
表5 第二层矩阵B2指标权重值

第二层指标体系B3、B4为二阶矩阵，根据其各因素间的重要性程度，得出P3、P4=(0.5，0.5)第二层指标权重：

P1=(0.14，0.44，0.28，0.14)

P2=(0.4，0.24，0.24，0.12)

P3=(0.5，0.5)

P4=(0.5，0.5)

根据上述计算，判断矩阵A、B1、B2、B3、B4所有模型所作矩阵的最大特征根均小于最大标准特征根，因此，上表各矩阵均有满意的一致性。

3) 计算各元素相对总目标的权重W：

W=(0.064 4、0.202 4、0.128 8、0.064 4、0.124、0.074 4、0.074 4、0.037 2、0.05、0.05、0.065、0.065)

4) 根据专家打分情况设各元素的满意度分别为：R(C1)=0.85，R(C2)=0.95，R(C3)=0.85，R(C4)=0.9，R(C5)=0.95，R(C6)=0.9，R(C7)=0.9，R(C8)=0.8，R(C9)=0.95，R(C10)=0.8，R(C11)=0.95，R(C12)=0.9。

则该主炮系统的技术状态效能值为

2.2 应用模糊综合评判模型进行效能评估

1) 建立两个层次的评价指标集，设第一层模型评价集为U={u1,u2,…,un},其中指标ui(i=1,2,…,n)是第一层次中的第i个指标，ui由第二层次中的m个子指标决定，即ui={ui1,ui2,…,uim},其中指标uij(i=1,2,…,n;j=1,2,…,m)是第i个指标的第j个子指标。

2) 设置评语集。根据对舰载武器系统技术状态效能可能的评价描述，假设评判等级数为4，即V={Ⅰ,Ⅱ,Ⅲ,Ⅳ}分别表示差、中、良、优4个等级，如表6所示。

表6 技术状态效能评级

根据评估体系和问题，确定该体系相对于各个指标的模糊评语如表7所列。

1) 计算模糊评语Bi。这里将运用模糊评价的两种算法进行计算—主因素突出型算法和加权综合型算法。

加权算法采用矩阵加权算法计算。

主因素突出型算法根据下列公式计算：

ai∧rij=min(ai,rij)

ai∨rij=max(ai,rij)

根据上表所列的数据，计算第一层各个指标的uir的模糊评语Bi(i=1,2,3),其中

主因素计算：

B1主因素=[0.5,0.3,0.2,0.1]

加权算法计算：

B1加权=[0.47,0.32,0.13,0.08]

B2、B3、B4的取值按照以上方法进行计算，其值分别为：

B2主因素=[0.4,0.3,0.2,0.1]

B2加权=[0.56,0.23,0.14,0.07]

B3主因素=[0.5,0.4,0.1,0.1]

B3加权=[0.55,0.3,0.10,0.05]

B4主因素=[0.5,0.4,0.1,0.1]

B4加权=[0.55,0.3,0.10,0.05]

2) 计算模糊评语B

将各个Bi组成为总的模糊矩阵R后，再计算整体评价方案的总的综合模糊评语B。按主因素突出型算法得出：

对此结果进行归一化处理得：

B主因素=[0.5,0.3,0.2,0.1]=

按加权综合型算法计算得出：

[0.573,0.289,0.127,0.071]=

3) 将模糊评语B转化为总得分

根据专家的意见给各级评语Bi确定一个权数Wi，

例如令W1=100，W2=75,W3=50,W4=25。这样，上面评估的方案的总得分为：

0.2×50+0.1×25=85

0.127×50+0.071×25=87.1

在此评价方案中，主因素型和加权型两种算法的综合结果差别不大，但可以看出，主因素型算法得出的综合结果比较粗糙，而加权型算法得出的综合结果则比较细致。因此，此评价方案中可以以加权算法得出的综合结果作为最终评价结果。根据以上所求评判集结果，对照其效能评语等级表，确定该舰载武器系统技术状态效能为优。

表7 各个指标的模糊评语

3 结论

通过对舰载主炮武器系统的构成和特点进行分析，给出了技术状态评估体系模型。同时，应用AHP法和模糊综合评价法对其技术状态效能进行估，通过对比两种方法的应用过程和评估结果，不仅证明了其方法的可行性，更从中发现针对任务性质和装备技术状态的不同需求，选用合适的评估方法能得到很好的效果。在实际训练和作战任务时，由于任务较复杂，对技术状态要求较高，应选用结果较精确，过程较复杂的综合评价法；而在日常装备检查及模拟训练任务中，由于任务单一，对技术状态要求较专项任务低，应选用方便快捷的AHP法。因此，结合现阶段，舰艇执行不同任务所需的不同技术状态，选用合适的评估方法能极大地提高评估效率。同时，也为下一步应用于其他舰载武器系统技术状态效能评估研究打下良好基础，具有较强的军事应用价值。

[1] 杨伦标,高英仪.模糊数学原理及应用[M].广州：华南理工大学出版社,1998.

[2] 胡永宏,贺思辉.综合评价方法[M].北京：科学出版社，2000.167-200.

[3] 徐昌文.模糊数学在船舶工程中的应用[M].北京:国防工业出版社，1992:122-124.

[4] 张杰,唐宏,苏凯,等.效能评估方法研究[M].北京：国防工业出版社,2009.

[5] 吴智辉,张多林,谢磊峰．基于层次分析法的防空信息战效能评估[J].系统工程与电子技术，2004，26(2):209-211.

[6] 王龙涛,陶熹,基于改进层次分析法的舰载信息系统作战效能评估[J].舰船电子对抗，2009，32(1)：48-50.

[7] 周勇,洪贞启.层次分析法在潜艇作战能力评估中的应用[J].情报指挥控制系统与仿真技术,2004,26(3):42-45.

[8] 耿俊豹,金家善,万延斌．基于多层模糊模型的舰船技术状态评估方法研究[J].舰船科学技术，2004，26(6):18-19.

[9] 张松林,刘宁,李波.模糊综合评判方法及其在机械设计中的应用.武汉理工大学学报:交通科学与工程版，2001，25(2):150-152.

[10] 王钦,文福拴,刘敏.基于模糊集理论和层次分析法的电力市场综合评价[J].电力系统自动化，2009,33(7)；32-37.