一种基于模糊推理的导航自适应滤波算法

戴 卿，叶城睿，马云峰,2

(1.重庆水利电力职业技术学院 建筑工程系，重庆 402160；2.重庆交通大学 土木工程学院，重庆 400074)

0 引言

GNSS/SINS组合导航系统因其良好的互补性、定位精度和可靠性，近几年来在军事与民用领域得到了广泛的应用[1]。拓展卡尔曼滤波(Extended Kalman Filter，EKF)是状态最优估计的有效算法，当GNSS/SINS导航系统的数学模型准确，且忽略计算误差时，解算结果最优，否则会降低精度，甚至引起发散问题[2]。由于动态载体在观测中会出现多径现象，导致GNSS量测噪声统计模型的不准确和时变性，尤其在长时间持续机动状态工作中，这种影响更不容小觑。有学者进行了大量反复的试验研究，但发现建立在实际工作时的精确量测噪声模型仍很困难[3]。

为解决此类问题，有效的数据融合算法成为众多学者的研究热点。由此产生了一系列在滤波计算中通过量测新息在线修正噪声随机模型的自适应滤波技术，有衰减记忆因子算法，平方根滤波、Husa-sage滤波等，在提高滤波精度、改善系统鲁棒性等方面取得了一定成效[3-4]。 H∞滤波不限制系统先验信息，但是计算负担较大。基于神经网络学习的自适应滤波算法，精度较高，但计算量较大，应用对象受限[5]。近年来一系列将EKF与模糊推理系统 (Fuzzy Inference System，FIS) 相结合的智能算法被众多学者提出，如相关因子法、协方差法、衰减因子法和指数加权法等，并广泛应用于计算机、自动化、电子技术等领域，但在导航解算上的研究则较为鲜见[6]。

本文受上述研究启发，提出一种基于模糊理论的自适应扩展卡尔曼滤波融合算法方案，通过计算量测新息所得实际方差与理论方差之比，并利用模糊推理系统对GNSS量测噪声统计模型实时在线估计和修正，有效解决了由于模型不准确导致的滤波发散现象，适应于量测噪声先验特性未知的时变系统。通过试验测试表明，相比于传统算法，新算法在时变量测噪声情况下，精度明显提高，计算负担小，能有效克服载体机动状态下的估计问题，改善滤波估计效果的稳定性和抗差性，易于工程实现。

1 常规组合导航EKF算法问题描述

对SINS/GNSS组合导航系统建模，得离散时间系统

Xk=Φk,k-1Xk-1+Wk
Zk=HkXk+Vk

(1)

式中，Xk为包含姿态、速度、位置、陀螺零偏和加速度偏置的15维状态量，Zk为姿态、速度和位置的9维组合观测量。Φk,k-1和Hk为状态转移矩阵和观测矩阵，Wk和Vk为过程噪声和量测噪声，具体设置见文献[7]。

这里通常假设过程噪声和量测噪声为零均值的高斯白噪声，其协方差阵为Q和R。然而，通过对组合导航系统的大量反复试验，发现量测噪声先验特性随环境变化，统计特征是未知的。当量测噪声模型不准确时，会使EKF滤波性能下降，严重时引起发散。因此,为解决这个问题，需设计自适应滤波技术。

2 基于模糊理论的自适应EKF算法

2.1 自适应EKF算法设计

依据文献[8-10]的研究思路，设计自适应EKF算法过程如下

Xk|k-1=Φk,k-1Xk-1

(2)

(3)

(4)

Xk=Xk|k-1+Kk(Zk-HkXk|k-1)

(5)

Pk=(I-KkHk)Pk|k-1

(6)

(7)

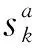
计算残差方差理论值

(8)

计算残差实测方差

(9)

rk=Zk-HkXk|k-1

(10)

式中，实测方差是对M个残差向量方差的开窗均值，窗口大小由经验获得。则比值μk为

(11)

2.2 模糊规则设计

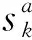
其采用的隶属度函数如图1和图2所示。

图1 FIS输入μk的隶属度函数

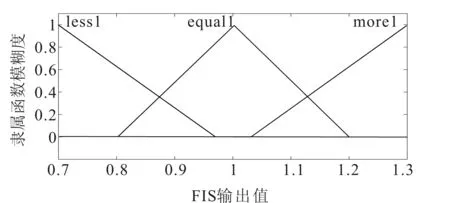
图2 FIS输出的隶属度函数

2.3 模糊度自适应EKF算法

综上所述，本文设计的模糊自适应EKF算法流程如图3所示。首先，由式8～式11计算残差方差的实际值和理论值的迹的比值；其次，对比值进行模糊化处理，得到模糊子集上对应的隶属度函数；最后，当量测噪声不平稳时，调整量测噪声协方差矩阵使其逐渐逼近于真实噪声水平。

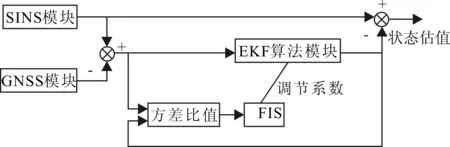
图3 基于模糊自适应的EKF算法流程

3 实验结果与分析

3.1 仿真测试

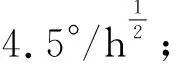
方案1：拓展卡尔曼滤波

方案2：基于模糊自适应的拓展卡尔曼滤波

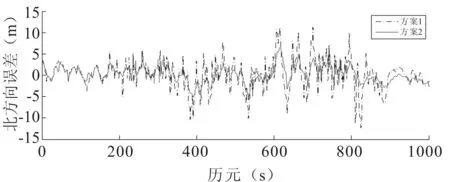
图4 北向定位误差曲线

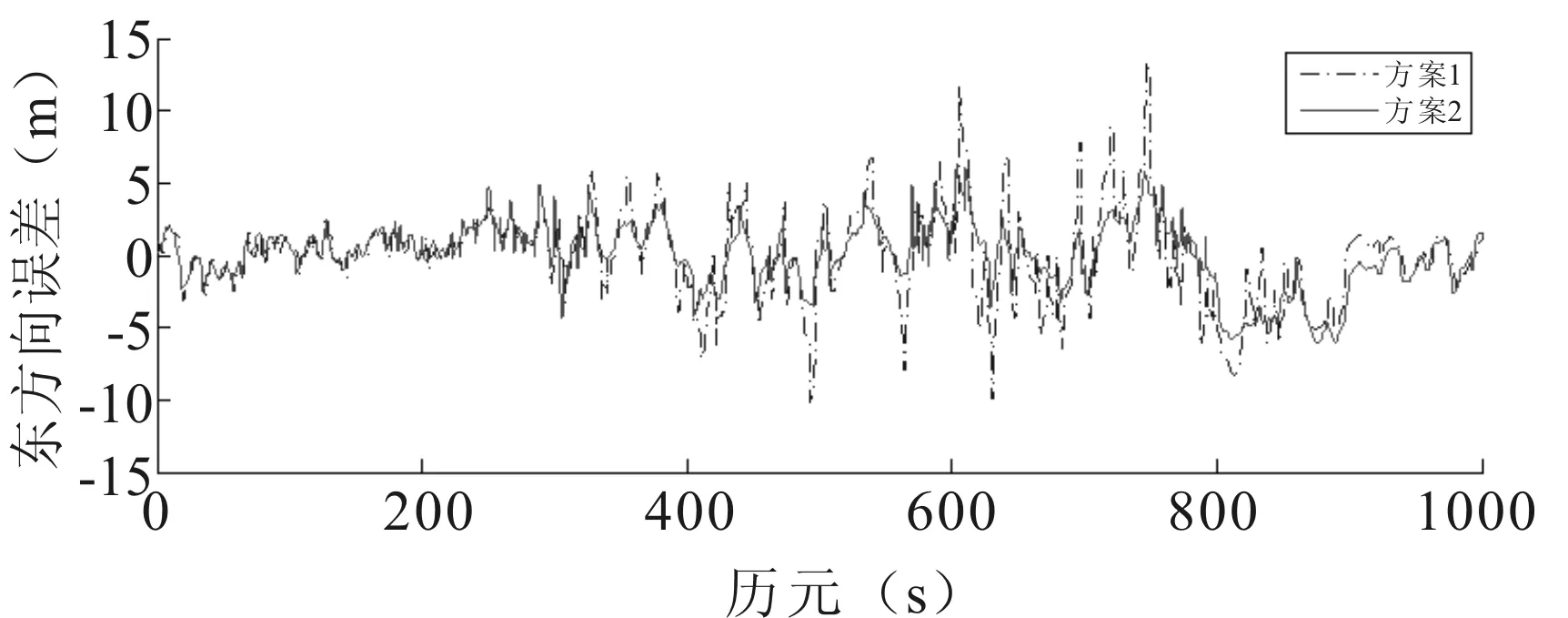
图5 东向定位误差曲线

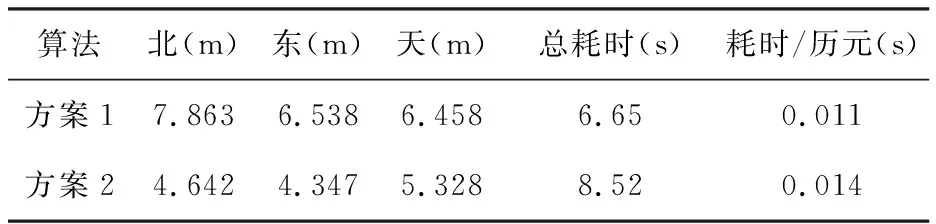
算法北(m)东(m)天(m)总耗时(s)耗时/历元(s)方案17.8636.5386.4586.650.011方案24.6424.3475.3288.520.014

由图4和图5可见，初始阶段因随机模型较为准确，因此两种滤波计算方案估计结果较为一致。在历元[200,800]期间，由于量测噪声发生两次突变，初始噪声协方差不能准确描述GNSS噪声数学统计特征，导致方案1的估计误差明显增大，而方案2是基于模糊逻辑的自适应滤波算法，可以在线调整噪声协方差，保证模型的准确性，在偏差较大处，有明显的纠偏作用，使得滤波结果仍能保持较高的精度，估计偏差在5 m以内，满足大多普通用户的需求。

为进一步证明算法的有效性，对历元[200,800]期间的实验情景进行了50次蒙特卡洛仿真实验，结果如表1所示。可见，方案2定位效果明显优于方案1，而耗时却没有明显增加。说明本文通过模糊理论改进的EKF算法能提高系统的抗差性，使得解算结果更为稳定，适合工程应用。

3.2 跑车试验

为进一步验证本文所提算法的有效性，进行了跑车实验。其中惯性装置采用MEMS IMU420C，GNSS接收机采用OEM-G2板卡，进行约10 min的数据测试，沿途经过树林、人工湖等可产生明显的多径效应，采用节3.1中的两种不同方案进行处理，解算结果如图6和图7所示。

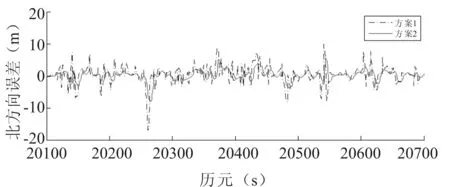
图6 北向定位误差曲线

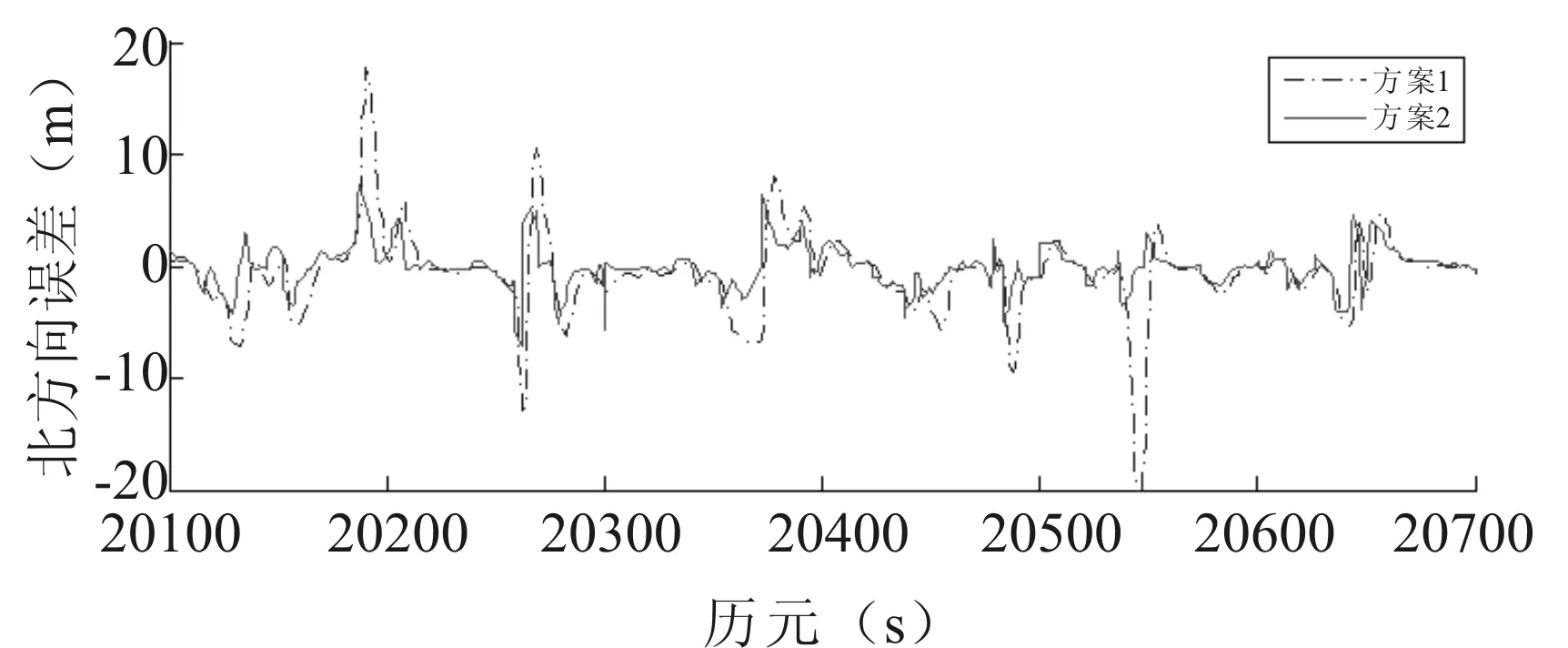
图7 东向定位误差曲线

从跑车试验结果来看，总体上新算法明显优于传统算法。图6中传统算法在北向位置误差优于10 m，最大误差为16.13 m。经过基于模糊逻辑改进的自适应拓展卡尔曼滤波处理后，北向误差优于5 m，最大误差为8.53 m。说明在采取基于模糊推理的自适应EKF方法之后，有效减轻了GNSS测量噪声统计模型不确定对滤波精度的影响，总体精度有进一步提升。将该算法用于时变性大，量测干扰不可知的导航中，可以发挥较好的导航定位性能。

4 结论

为改善GNSS/SINS组合导航系统在稳态突变或多路径影响严重的观测环境中作业时，量测噪声随机模型不确定导致的滤波性能下降问题，本文研究了一种基于模糊推理系统的自适应EKF数据融合算法。首先，借鉴模糊推理系统进行在线估计；然后，通过系统残差变化自适应调整噪声模型，完成时间噪声协方差阵的实时估计与修正。该算法运算简单，确保了导航计算的实时性，且估计误差收敛效果良好。最后，通过实验表明：将此算法用于GNSS/SINS组合导航数据融合中，在时变GNSS噪声情况下，对系统模型的依赖小，能较好的跟踪量测噪声方差，有效提高导航计算的精度和可靠性，对工程实践具有一定参考意义。

[1] 陈建峰.面向高动态环境的SINS/GPS高精度组合测量中的关键问题研究[D].南京:东南大学,2015:57-81.

[2] FARIZ O,FU L,LIN Y,et al.A new SINS/GPS sensor fusion scheme for UAV localization problem using nonlinear SVSF with covariance derivation and an adaptive boundary layer[J].Chinese Journal of Aeronautics,2016,29(2):424-440.

[3] 肖志涛,赵培培,李士心.基于INS/GPS组合导航的自适应模糊卡尔曼滤波[J].中国惯性技术学报,2010,18(2):195-198.

[4] 赵欣,王仕成,闫循良,等. 基于遗传模糊控制的智能自适应滤波算法[J].北京工业大学学报,2012,38(12):1893-1900.

[5] LI X,ZHANG W G.Multi-sensor integrated navigation for intelligent vehicles based on H∞ filter[J].Journal of System Simulation,2007,19(18):4168-4177.

[6] 高运广,王仕成,刘志国,等.一种基于遗传模糊推理的自适应容错滤波算法[J].中国惯性技术学报,2012,20(3):315-319.

[7] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2016:33-41.

[8] 曹梦龙,李振. 滤波增益模糊自适应调节导航算法[J].青岛科技大学学报(自然科学版),2017,38(5):101-106.

[9] 吕新知.FAST-SR-UKF算法及其在组合导航系统中的应用[J].计算机工程与应用,2015,51(6):254-259.

[10] 万振塬,杨功流,涂勇强.一种新型模糊自适应Kalman滤波器在组合导航中的应用[J].导航与控制,2017,16(2):81-86.

[11] 杨春,郭健,张磊,等.采用卡方检验的模糊自适应无迹卡尔曼滤波组合导航算法[J].控制与决策,2018,33(1):81-87.