泡沫经济危机动态预警研究
——基于房地产市场国际经验数据
, , ,2
(1.西安理工大学 经济与管理学院,陕西 西安 710054; 2.西安理工大学 印刷包装与数字媒体学院,陕西 西安 710054)
1 引言
近年来,泡沫经济现象频繁发生,典型的有80年代末90年代初日本的泡沫经济[1]。2007年美国的“次贷危机”,从房地产和金融业逐步蔓延到实体经济,又进一步殃及全球经济[2]。世界经济正在承受着由泡沫经济带来的一系列的问题。
现有研究主要停留在资产价格泡沫的预警方面。有关资产价格泡沫预警的研究可以归为两类:第一类是通过测度资产价格泡沫的大小对泡沫经济进行预警,如Mikhed和Zemcik[3],Chiang等[4],张玉双[5]利用面板数据模型分别测度了房地产泡沫和股市泡沫;陈长石和刘晨晖[6],史兴杰和周勇[7],李梦玄和曹阳[8]分别通过行为金融等新兴金融理论的视角,对房地产泡沫度进行了衡量。第二类是通过构建预警指标体系对资产价格泡沫进行预警。如Kamada和Nasu[9]通过几组先行指标和滞后指标构建了金融周期指数,可以提前1年预测资产价格泡沫的生成。而Ishikawa等[10]通过构建一组金融活动指数对资产价格泡沫预警。我国学者也通过先行指标、指示指标和滞后指标来对房地产市场泡沫进行定量分析[11,12]。然而这些资产价格泡沫的预警均是对一个国家的资产价格泡沫进行分析,Alessi和Detken[13]则综合了18个国家的数据对资产价格泡沫预警体系进行了检验。但是对于泡沫经济危机的预警,现有研究并没有明确的说明。
此外,在危机预警的研究方法上,较为常见的有指标预警、模型预警和人工智能系统预警。Berg等[14]通过实证分析认为模型预警的准确性要远高于指标预警。现阶段主要有四种危机预警模型,分别为KLR信号分析法[15],STV截面回归模型[16],马尔科夫区制转换模型[17],二元离散选择模型[18]等。但这四种模型均是针对单一阶段的危机进行预警,不能刻画出危机发展的动态过程。自20世纪90年代以来,人工智能系统方法在危机预警研究中的地位日益凸显。其中包括神经网络模型、遗传算法、支持向量机等方法[19,20]。然而人工智能方法需要大量的样本作为基础,我国甚至世界范围内泡沫经济的发生并不是大概率事件,不适用于本文对于泡沫经济预警模型的研究。
通过以上综述可以看出,现有研究主要以资产价格泡沫预警的研究为主,但针对泡沫经济预警的相关研究较少。本文试图在梳理和识别泡沫经济发展过程的基础上,通过多元有序logit模型与状态空间模型相结合的方法将泡沫经济发展的动态过程联系起来,建立基于房地产市场数据的泡沫经济动态预警机制,以防范资产价格泡沫过大引起的泡沫经济危机。此外,现有资产价格泡沫的主要载体为股票和房地产市场,而在资产价格泡沫向泡沫经济演化的路径中,房地产价格泡沫由于与银行信贷的直接联系,可能使银行体系在毫无征兆的条件下发生危机,进而引发更加严重的泡沫经济危机[5]。因此,本文根据房地产价格泡沫向泡沫经济演化这一路径来说明泡沫经济的预警。
2 泡沫经济的发展过程及识别
2.1 理论分析
根据扈文秀和席酉民[21]的研究,泡沫经济的发生是以资产价格泡沫的发生为基础,具体演化路径如图1所示。
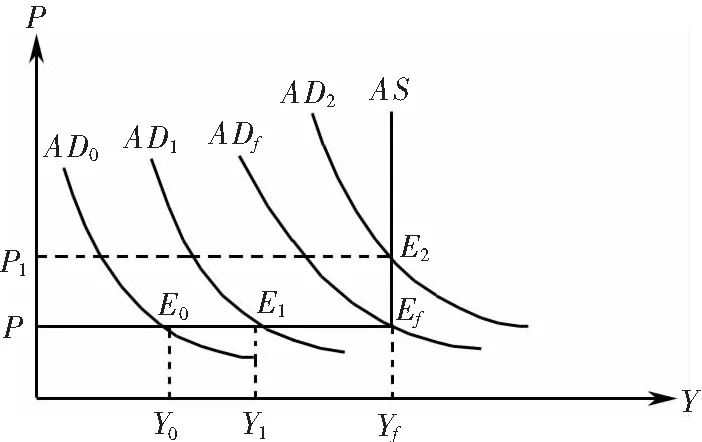
图1 资产价格泡沫向泡沫经济的演化
当市场中出现资产价格泡沫现象时,并不是所有的资产价格泡沫现象都是对经济有害的。适度的资产价格泡沫的存在会刺激社会的有效需求,进而增加国民收入。如图1所示,AD0为初始的总需曲线,AS为总供给曲线,Y为均衡的产出。假设资产价格泡沫使得社会的有效需求从AD0提高至AD1,这时社会总供给增加,并且均衡产出由Y0提高至Y1,经济增长稳定。但是这一经济的稳定增长使得人们对经济的预期更加乐观,进而形成更大的投机需求,导致资产价格泡沫更大,进而产生更多的社会总供给。这一过程不断循环,直到达到充分就业的有效需求ADf和充分就业下的均衡产出Yf。在此之后,总需求受到资产价格泡沫的拉动而继续升高,从而超过了ADf,即超过了充分就业的有效需求。此时,市场中出现了生产要素的紧缺,造成了经济的虚假繁荣现象,即泡沫经济现象。由此我们可以看出,泡沫经济的发生一定是以局部的资产价格泡沫的发展为前提。因此,本文将泡沫经济预警阶段根据其发展过程分为经济平稳发展阶段、资产价格泡沫阶段和泡沫经济阶段。在构建预警模型之前,首先应对泡沫经济不同发展阶段进行划分和识别。
2.2 泡沫经济不同发展阶段划分
基于数据的可得性和代表性,本文选取36个国家作为研究样本,样本区间为1996年1月至2016年3月,在此区间内尽可能地包括了金融危机,资产价格急速上涨,宏观经济大幅波动等重要经济趋势。首先,本文通过COBS模型和潜在产出模型分别对房地产价格泡沫区间和泡沫经济区间进行估算。
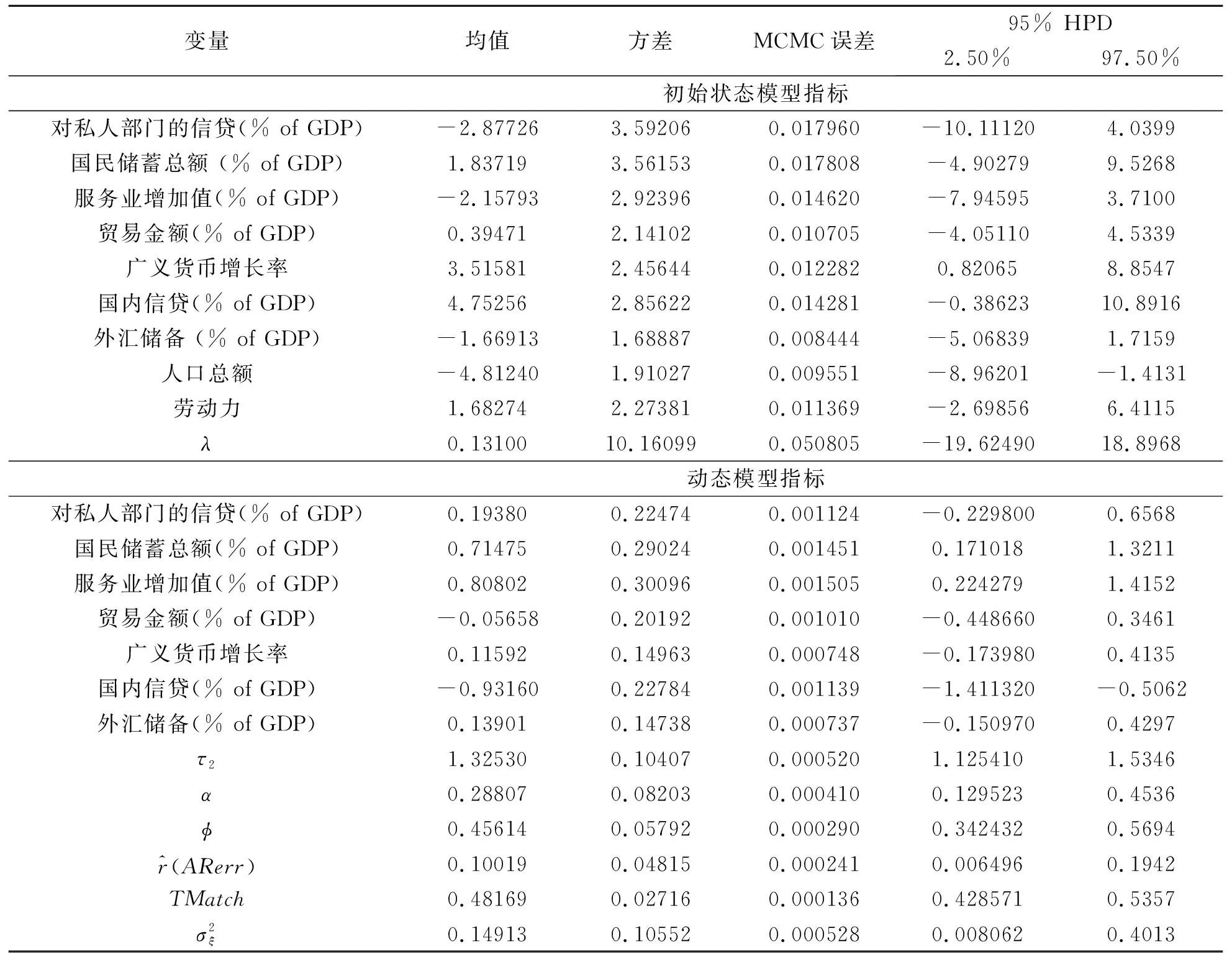
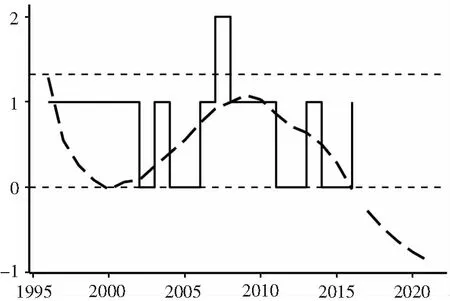
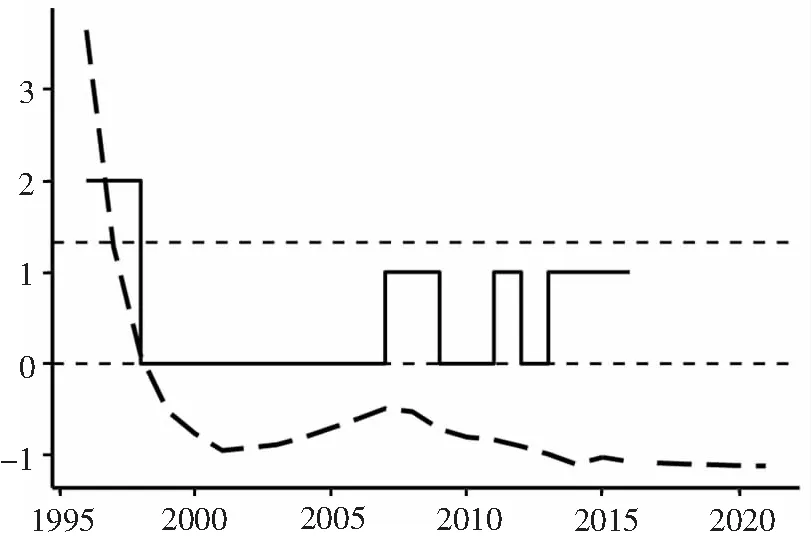
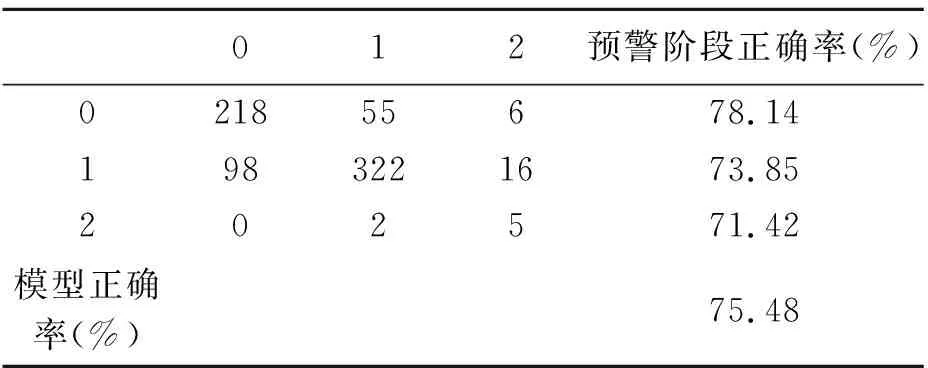
对于房地产价格泡沫区间的计算,其简要过程和估算结果如下:设给定变量X=x,通过条件分位数函数gτ(x)构建一个平滑问题,即Y的第τ个条件分位数gτ(x)为x的函数,即P(Y 由于泡沫经济的发展是一个循序渐进的阶段性过程,本文对于泡沫经济的预警思路如下:首先,计算得出泡沫经济发展过程中不同阶段的预警阈值。其次,预测未来的经济状态,进而对比预测得到的经济状态与阈值,得出一定期间后经济状态处于泡沫经济发展的哪一阶段,根据不同的阶段采取控制措施。当我们根据以上预警思路构建泡沫经济预警模型时,有三个核心问题亟待解决:第一,如何将泡沫经济的发展过程联系起来。第二,如何解决初始观测值的问题。在进入观察窗口的一个经济体的经济状态并不是最初的经济状态,我们需要构建初始状态模型来解决这一问题。第三,如何预测未来的经济状态。为此,本文通过构建潜在动态有序模型和预测模型来解决以上问题。 本文中潜在动态模型的意义在于将泡沫经济发展的动态过程联系起来,将离散变量转化为连续变量。由于面板数据中第一个时间点的观测值并不能代表动态过程的初始状态,因此初始状态的问题,也将考虑到模型当中。据此,本文的动态模型包括以下两个部分,贝叶斯潜在动态有序logit模型构建和初始条件模型构建。 (1)贝叶斯潜在动态有序logit模型构建 假设经济状态被设定为一种潜在变量zit,而yit为可观察到的经济的分类状态,τ1、τ2为每一经济状态下的阈值。因此,分类状态yit可以看作潜在连续变量zit和阈值τ共同生成的离散变量。构建的多元有序logit模型如下 其中i=1,K,N;t=0,K,T;-∞<τ1<τ2<+∞。当经济状态平稳时,yit=0;当市场中出现资产价格泡沫时,yit=1;当经济市场中出现泡沫经济时,yit=2。我们预设τ1=0以确定模型参数。 由此,我们得到潜在经济状态变量的动态模型 zit=φzit-1+βxit+ξi+εitt=1,…,T (2)初始观测值模型构建 假设初始值可能取决于可观测的经济变量xi。此外,为了捕获无法观测的经济变量对初始值的影响,我们通过纳入内生初始值zi0,构建初始值的拟合模型 其中wi是由进入样本窗口的首个经济变量xi0组成的初始协变量向量。ξi为个体效应。不可观测个体效应对初始值的影响通过λ获得,它允许不可观测个体效应对初始值的影响大小可变。此外,初始值模型的随机误差εi0与其他误差无关。 本文采用不包含季节项的Holt-Winter指数平滑法对潜在变量时间序列进行建模。同时,借助状态空间模型对未来潜在变量进行预测。我们采用阻尼趋势平滑法对潜在变量进行预测,模型构建如下 zt=1t-1+φbt-1+εt 假设ζt满足均值为0,方差为σ2的高斯独立同分布。 本文通过国际面板数据解决样本数量的问题,基于数据的可得性和代表性,尽可能多地选择样本国家以扩大样本量。本文选取36个国家作为研究样本,样本区间为1996年1月至2016年3月,所有的数据均为季度数据,取自万德数据库,世界银行数据库和锐思数据库。 在进行实证分析之前,首先要对纳入预警模型的经济指标进行选择,即对预警模型中的解释变量进行选择。本文最终选取包括宏观经济基本面指标,金融财政指标,金融体系健康程度指标以及货币政策指标,共4大类47个指标作为初选指标。为了减小模型估计结果的不确定性,本文利用贝叶斯平均方法对指标进行筛选。其模型为一个包括n个观测值和k个解释变量的回归方程 Y=c+α1x1+α2x2+…+αnxn+ε 其中Y为被解释变量,xi为解释变量。本文采取扩散单位信息先验分布来提高先验分布的稳健性。即增加或者减少一个解释变量的概率均为0.5,其意义为事前不对任何变量做出具有偏好的选择。对于每一组变量,我们的报告结果包含后验概率,后验均值,后验标准差。最终的估计结果显示,45个解释变量中,5个变量的后验概率高于0.5。综合考虑数据可得性和结合后验概率最高的前4个最优模型所包含的变量,最终确定动态模型中的解释变量为7个变量,其中包括对私人部门的信贷/GDP,国内信贷/GDP,国民储蓄总额/GDP,服务业增加值/GDP,外汇储备/GDP,贸易金额/GDP,广义货币增长(M1)。 上文对1996年至2016年间的36个国家的经济数据进行分析,最终得到最适合预警模型的7项指标作为解释变量,获得了共21年36个国家的平衡面板,研究样本共计756个年度观测值。本文结合计算出来的泡沫经济发展过程中的不同经济区间,借助马尔科夫连蒙特卡洛方法(MCMC方法),依据经济预警指标对预警模型进行参数估计,对经济状态进行识别。为了确保阈值τ的单调性,我们以递归的方式设置阈值的先验形式,将前一个阈值加上正随机数υτ获得下一个阈值。为了保证随机数υτ大于0,本文将第一个阈值规范化为0以便于阈值先验分布设置:τ1=0,τ2=τ1+υτ,υτ~Exp(1)。 本研究通过MCMC抽样算法,设置了两条马尔科夫链,分别进行了500000迭代抽样,其中间隔取为25,即迭代25次进行1次监测。通过对模型中各个参数的实时监测,每个参数得到了40000个监测样本的马尔科夫链迭代图,以及均值、方差、MCMC误差、2.5%分位点、中值数和97.5%分位点等相应的计算结果,表1给出了参数估计结果。 表1 参数估计 (1)模型结果分析 本文以中国和日本为例,说明动态预警的分析过程。如图2和图3所示。 图2 中国泡沫经济预警 图3 日本泡沫经济预警 图中阶梯状的实线为经济状态实际值的拟合值,曲线为经济状态的预测值,与坐标轴平行的虚线为阈值,即阈值0和1.32530。我们可以通过经济状态的预测值与实际值进行对比,参照预警阈值来确定经济状态到达哪一阶段。以中国为例,从预警图中我们可以看出,在2005年以后,房地产价格的实际状况达到了一个峰值状态,经济状态的预测值虽大于阈值0,但是依旧小于阈值1.32530,这说明市场中已经产生了资产价格泡沫,但是并没有达到泡沫经济的状态,这与我国的实际情况相符。日本是世界上少数几个承认经历过泡沫经济的国家之一。从图3的日本预警图中我们可以看出,1995年之前经济状态从极高的阶段呈急速下降状态,而在1996年至1997年间,日本的经济泡沫消失,经济状态持续低迷。这也与日本的实际情况相吻合。20世纪80年代后期至90年代,日本经历了前所未有的泡沫经济现象,直到1992年泡沫经济崩溃,经济从此以后陷入萧条状态。 (2)有效性检验 本文通过分类识别的错误率对泡沫经济预警的有效性进行检测。如表2所示,横轴的0,1,2分别代表真实情况的经济状态平稳时期、资产价格泡沫时期和泡沫经济时期。纵轴0,1,2分别代表预警模型计算得到的经济状态平稳时期、资产价格泡沫时期和泡沫经济时期。以此分别计算预警模型在不同阶段的预警的正确率,最终得到整个预警过程的正确率。 表2 泡沫经济预警模型正确率 根据本文的预警模型,对于经济状态平稳阶段、资产价格泡沫阶段和泡沫经济阶段,其识别的正确率分别为78.14%,73.85%,71.42%。而对于整个泡沫经济发展过程预警的正确率为75.48%。整体预警效果较为准确。根据预警结果我们可以看出,本文的模型对于识别泡沫经济具有较高的正确率。在36个样本国家中,有5个国家出现了泡沫经济现象,分别是日本、芬兰、泰国、墨西哥和美国。其中日本、芬兰、泰国和墨西哥4个国家的泡沫经济区间与已有文献中对于泡沫经济的描述一致。但是现有文献对于美国是否发生过泡沫经济并没有统一的结论。根据本文的预警模型,美国在次贷危机前出现过泡沫经济危机。 泡沫经济危机预警问题对微观行业价格和整个宏观经济都具有重要意义。本文构建的动态泡沫经济预警模型,不仅可以根据泡沫经济的发展过程对泡沫经济危机进行检测和预警,将泡沫经济遏制在初期阶段,更能在已经产生资产价格泡沫后对泡沫经济危机的发生进行预警,以防止更加恶劣的泡沫经济危机的爆发。与以往的危机预警研究相比,本文的主要研究成果如下: (1)在研究内容上,现有研究主要关注资产价格泡沫的预警,几乎没有对于泡沫经济的预警。本文对资产价格泡沫发生后可能会引发的泡沫经济进行预警,扩充了现有对于价格泡沫预警的研究领域。 (2)分析泡沫经济发生的动态特征,梳理与泡沫经济的发生有相关性的经济特征。从宏观经济基本面、金融财政指数、金融体系健康程度和货币政策四个方面分析对资产价格泡沫和泡沫经济的影响。 (3)在建立泡沫经济预警模型的过程中,分别通过COBS模型识别出各个国家的房地产价格泡沫区间,通过构建多参数动态系统模型进行Kalman滤波分析,估计潜在产出,从而得到泡沫经济区间。为分阶段动态预警模型的建立提供了现实基础。 (4)借助贝叶斯动态模型和状态空间模型构建泡沫经济动态危机预警系统,建立了分阶段的动态预警模型,实现了对危机的发展过程进行跟踪分级预警。并以数据统计为基础,反映了一个国家经济状况从平稳发展到泡沫经济危机的渐进过程。最后对经济状况进行预测,为决策部门提前预见危机状态,制定调控政策提供科学依据。 本研究由于数据的限制,今后有尚待完善的地方:进一步对数据进行更加细致的划分,如将数据分为长期数据和短期数据,分别进行模型估计,以提高模型的准确性。除此之外,将继续搜集数据增加样本数量,不断完善模型精度。 [1] 邢天添.反思日本泡沫经济——从国际金融协调视角看中国的选择[J].中央财经大学学报,2015,(11):88-95. [2] 雷良海,魏遥.美国次贷危机的传导机制[J].世界经济研究,2009,(12):24-31,88. [3] Mikhed V, Zemcik P. Testing for bubbles in housing markets: a panel data approach[J]. The Journal of Real Estate Finance and Economics, 2009, 38(4): 366-386. [4] Chiang M C, Tsai I C, Lee C F. Fundamental indicators, bubbles in stock returns and investor sentiment[J]. The Quarterly Review of Economics and Finance, 2011, 51(1): 82- 87. [5] 张玉双.我国地区房地产价格泡沫的测度[J].统计与决策,2016,(5):129-132. [6] 陈长石,刘晨晖.利率调控、货币供应与房地产泡沫——基于泡沫测算与MS-VAR模型的实证分析[J].国际金融研究,2015,(10):21-31. [7] 史兴杰,周勇.房地产泡沫检验的Switching AR模型[J].系统工程理论与实践,2014,34(3):676- 682. [8] 李梦玄,曹阳.我国房地产市场泡沫的测度及成因分析——基于行为金融理论的视角[J].宏观经济研究,2013,(9):86-91. [9] Kamada K, Nasu K. The financial cycle indexes for early warning exercise[R]. Japan: Bank of Japan Working Paper Series, 2011. [10] Ishikawa A, Kamada K, Kan K, et al.. The financial activity index[R]. Japan: Bank of Japan Working Paper Series, 2012. [11] 谢经荣.地产泡沫与金融危机——国际经验及其借鉴[M].北京:经济管理出版社,2002.298-301. [12] 师应来,王平.房地产预警指标体系及综合预警方法研究[J].统计研究,2011,28(11):16-21. [13] Alessi L, Detken C. Quasi real time early warning indicators for costly asset price boom/bust cycles: a role for global liquidity[J]. European Journal of Political Economy, 2011, 27(3): 520-533. [14] Berg A, Borensztein E, Pattillo C. Assessing early warning systems: how have they worked in practice[J]. IMF Staff Papers, 2005, 52(3): 462-502. [15] Kaminsky G, Lizondo S, Reinhart C M. Leading indicators of currency crisis[J]. IMF Staff Paper, 1998, 45(1): 1- 48. [16] Stenkat J, Krautwald-Junghanns M E, Schmidt V. Financial crises in emerging markets: the lessons from 1995[J]. Brooking Papers on Economic Activity, 1996, (1): 147-215. [17] Hamilton J D. Regime-switching models[J]. The New Palgrave Dictionary of Economics, 2008, (2): 202-209. [18] Frankel J A, Rose A K. Currency crashes in emerging markets: an empirical treatment[J]. Journal of International Economics, 1996, 41(3- 4): 351-366. [19] Lin C S, Khan H A, Chang R Y, et al.. A new approach to modeling early warning systems for currency crises: can a machine-learning fuzzy expert system predict the currency crises effectively[J]. Journal of International Money and Finance, 2008, 27(7): 1098-1121. [20] 周辉仁,唐万生,任仙玲.基于递阶遗传算法和BP网络的财务预警[J].系统管理学报,2010,19(1):1- 6. [21] 扈文秀,席酉民.经济泡沫向泡沫经济的演变机理[J].经济学家,2001,(4):107-112. [22] Doménech R, Gomez V. Estimating potential output, core inflation, and the NAIRU as latent variables[J]. Journal of Business & Economic Statistics, 2006, 24(3): 354-365.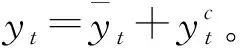
3 模型设定
3.1 动态模型设定
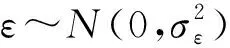
3.2 预测模型
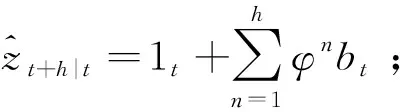
4 实证分析
4.1 数据来源和解释变量选择
4.2 参数估计
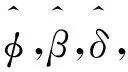
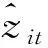
4.3 模型的有效性分析与检验
5 结论与展望

