空间相关会影响股指的国际投资决策吗？

, ,

(1. 华南理工大学 工商管理学院，广东 广州 510640; 2.广西大学 数学与信息科学学院，广西 南宁 530004)

1 引言

股市指数(下文简称股指)作为股票市场价格变动的指标，能实时反映股市的变动规律。伴随着世界经济一体化和金融一体化进程，国际资本流动更加快速，世界各国经济得到巨大发展。但与此同时，各国经济波动的同步性和股市波动的全球化已变得更明显、更为广泛。2016年伊始，全球股市暴跌，然而进入3月，全球股票市场全面上涨，新兴市场更是进入了一场大反弹。好景不长，4月下旬股市普遍开始下跌，几乎抵消了2016年以来的上涨。股票市场上演惊天大逆转，金融市场的联动性威力再现，联动性再次成为近期全球股市的主题。

目前，已有众多文献用传统的时间序列分析方法研究股指的联动性，研究内容主要集中在股指之间是否存在相关性以及如何引导。研究的模型及方法基本囿于传统的统计方法。研究结果一致认为经济贸易全球化以及金融市场的一体化是各国股指联动的主要原因，可从经济基本面、投资者行为及金融危机等极端事件等方面来解释。这些模型和方法固然能对股指相关性提供部分证据并具有一定的说服力。但是，现实中经常出现一些实体经济依赖并不紧密的国家之间也发生了股指联动性，且历次联动性在不同程度上表现出集聚性或区域性。这些牵涉到地域空间的深层问题已经超越了传统计量经济学的研究范畴，传统理论已不能解释这类现象。因此，需引入能够考虑时空相关的空间计量经济模型来研究股指联动过程。

本文考虑从以下几点来展开研究：(1)研究股指空间相关性的原因及作用机理。同时，为了使研究更具有一般性，所以在以下几个方面做了一些工作：第一，数据选取方面：与股指空间联动相关的文献在研究时间范围内局限于金融危机阶段，而本文却采用更广泛的时间范围，同时包括危机阶段及金融发展相对平稳阶段。第二，研究的对象则由以往文献限定于少数发达国家或地区的股指扩展为43国股指，研究对象既涵盖发达市场，也涉及新兴市场中的股指，因此研究范围更广泛、更具代表性。第三，空间权重设定方面：提出一种空间经济权重设定办法。该经济权重将根据不同空间单元经济变量的相对距离来构造，并且提出当空间单元即使不相邻，也会存在经济联系。(2)通过对时空/时间序列相关系数进行比较，分析论证两类股指相关性在各阶段所发挥作用的大小。本文研究结果可为企业或个人进行国际股指投资提供决策依据。

2 文献回顾与理论假设

近年来，一些文献已采用空间计量经济学研究股指相关性[1～5]。虽然这些研究取得较多成果，但其仍存在不足之处：研究模型或仅从空间截面进行分析，研究样本或局限于少量发达市场的股指，研究的时间范围或局限于某个金融危机阶段。那么，更大范围的市场之间，以及新兴国家之间的股指是否存在空间相关？这个问题依然还没得到解决。但与此同时，却有学者提出，空间计量经济学是研究区域经济的一门科学，将其运用在股票市场不甚合理。鉴于此，本文选取43国股指来对其空间相关性进行检验与机理探讨。根据Tobler[6]提出的地理学第一定律，本文首先提出股指之间存在空间相关关系的几点理由：

(1)股指之间由于经济或政治文化制度等方面的相似性而产生空间相关性。具体来说，经济运行模式及经济制度等方面的接近性和政治文化方面的相似性，会使国家之间出现不同形式的合作与分工。经济、政治制度方面的相似性越强，它们之间经济来往则越密切(常常会形成某种形式的经济同盟)，而反应经济晴雨表的股指间相关性越强；反之，相关性越弱。

(2)截面上投资者互相竞争和合作。现实中，一些国家拥有较丰富的资源禀赋或较合理的经济结构，易将其他国家的技术、劳动力、信息等方面的资源大量吸引进来，从而使本国企业快速发展利润提升，反映其利润变动的股价跟随上涨；反之，股价跟随下跌。最终形成股指间空间负相关关系。

(3)溢出效应的存在。如某国大量投资基础设施建设，或引入先进的科技人才队伍等措施，从而带动本国相关企业收益加大，股票价格上升。其他国家的企业由于与该国有商品、技术、劳动力等方面资源往来，从而经济效益也随之增长，股指上涨，股指呈现高值与高值正相关关系。相反，与之无交往的国家效益下滑, 股指呈现高值与低值负相关关系。事实上，邸倩和蒋海[7]也证实了股指溢出效应的存在。为此，本文提出第1个待检验的假设：

H1股指之间由于在经济、政治或文化制度等方面的相似性而存在空间相关性，且相关性呈现异质性现象。

另外，对不同国家、地区股指间相关性大小及其原因探究方面，已出现许多研究[8～13]。这些研究采用的方法主要为时间序列分析方法，研究的对象集中在发达市场，研究的结论也已基本达成一致：经济贸易全球化以及金融市场的一体化是各国股指产生相关性的主要原因，可以从经济基本面来进行解释，也可从投资者行为因素来解释，金融危机等极端事件会增强各国股指间相关性。但在空间相关性方面成果相对较少，虽有武占云等[3]研究表明经济/金融危机加剧了各国股指之间的空间相关性，宏观基本面是金融危机传导过程的主要影响因素。Gong和Weng[14]运用时空面板模型来对股指间联动性进行分析，研究表明股指间的联动不仅通过经济基本面因素进行传导，还通过外界市场冲击、市场资本化率等因素传导。其它一些研究由于空间回归中选取不同的自变量，而得出不同的结论[1,2,4,5,14]。鉴于此，本文参照大多数文献提出的股指间相关性传导因素，即宏观经济变量作为自变量来建立空间面板回归模型，探讨引起股指空间相关的因素及作用机理。为此，本文提出第2个待检验的假设：

H2股指间空间相关性作用的传导途径为GDP增长率等宏观经济变量。

事实上，近几年空间计量经济模型开始成为股指相关性研究的一个热点。那么，原有的时间序列统计分析在新的模型下是否适用？股指之间的相关性到底是由时间序列相关引起，还是空间相关引起？二者谁在起主导作用？新兴市场与发达市场间股指相关性如何，相关性大小在金融危机与金融相对平稳发展阶段是否稳定？诸如此类问题还鲜有研究。原因可能有两方面：一方面由于许多文献还受制于区域科学对“空间”概念的传统定义，将空间计量经济学研究严格地限制在自然地理的空间范畴内，认为空间计量经济学这一区域经济学科的方法不适用于金融业这一非实体经济。另一方面可能受研究方法所限，因为复杂形式的空间计量模型中参数估计方法、检验方法等比较缺乏，在进行参数估计时存在一定的难度。比如对高维度空间权重下的时空相关面板模型的参数估计、空间面板的平稳性检验等问题目前还没有统一、成熟的工具和软件去实现，这给学者们进行研究带来一定的阻力。基于上述理由，本文提出第3个待检验的假设(分为两个对立假设)：

H3a绝大多数股指之间时间序列相关性较大，空间相关性较小。

H3b绝大多数股指之间时间序列相关性较小，空间相关性较大。

3 研究设计

3.1 样本选取、数据来源及变量界定

在样本选取方面，本文选取43国股指为研究对象，基于两方面考虑：一是数据的可获得性较好；二是研究范围能覆盖发达市场及新兴市场，这种基于广泛对象择取的研究更具有普遍意义。股指数据采用2006年12月～2015年12月的月数据，来源于Wind数据库。选取2006年12月为研究的起点是因为金融市场在该点之前还处于较平稳发展阶段；而之后至2015年，既有金融危机的动荡阶段，也有危机后的平稳发展阶段，数据的选择具有代表性。同时，根据金融大事件将数据分为5个阶段。最终形成的样本如表1所示。

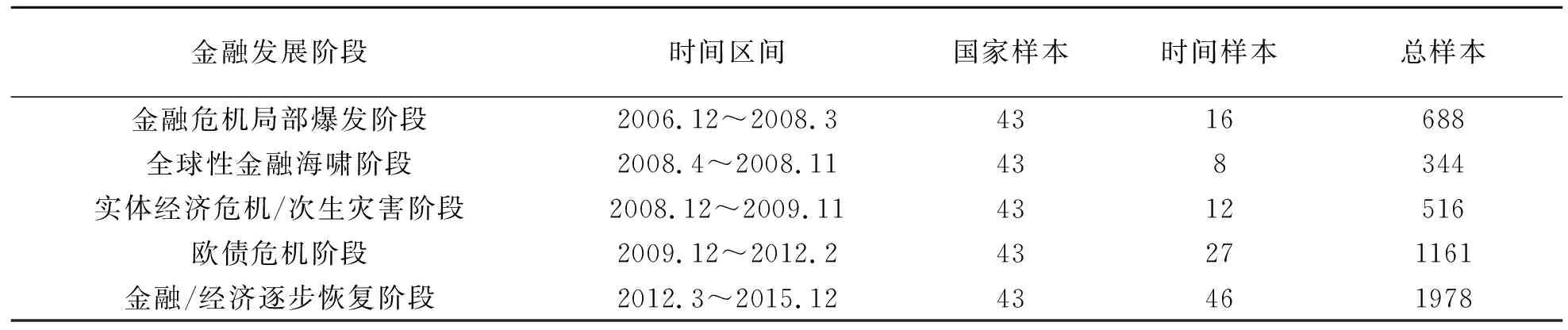
表1 空间相关性研究阶段划分及样本区间

注：43个国家按阿拉伯数字编号依次为：1阿根廷、2澳大利亚、3奥地利、4比利时、5巴西、6加拿大、7智利、8中国、9丹麦、10埃及、11芬兰、12法国、13德国、14希腊、15印度、16印度尼西亚、17爱尔兰、18以色列、19意大利、20日本、21大韩民国、22黎巴嫩、23马来西亚、24墨西哥、25荷兰、26新西兰、27尼日利亚、28挪威、29菲律宾、30波兰、31葡萄牙、32俄罗斯联邦、33沙特阿拉伯、34新加坡、35西班牙、36瑞典、37瑞士、38泰国、39土耳其、40乌克兰、41阿拉伯联合酋长国、42美国、43委内瑞拉。根据Wind数据库的统计分类，其中属于新兴市场的国家包括：1、5、7、8、10、14、15、16、21、22、23、24、27、29、30、32、33、38、39、40、41及43。其余为发达市场国家。

在变量界定方面，将股指收益作为因变量。而在解释变量方面，考虑到影响股指收益包括宏观和微观两个层面因素，而43国股指所受的宏观经济影响变量如GDP、CPI定义基本一致且较易收集数据，其他宏观变量如文化背景等或微观层面评价指标各有不同，难以界定统一的变量。因此，借鉴武占云等[3]的做法，本文从反映一国的宏观经济运行情况及相应经济政策变量入手，最终选取GDP增长率、通货膨胀增长率(CPI)、广义货币(M2)增长率、国际储备(Re)增长率、短期贷款利率(R)、进出口贸易水平(Trade)(以班轮航运连接指数来衡量)以及汇率(ExR)这7个变量指标作为时空回归分析的解释变量。另外，这些解释变量的数据来源中，前5个指标主要来源于新浪财经数据中的国际宏观经济数据，进出口贸易水平(Trade)则来源于联合国贸易和发展会议数据库，而汇率(ExR)来自新浪财经网及国家外汇管理局中的国际经济数据。此外，进行空间相关性检验及空间回归分析时，还需一个外生变量，即空间权重。借鉴已有的研究成果，同时考虑到数据的可获得性，本文以各阶段GDP经济总量相对距离为基础建立空间权重。

3.2 实证模型

进行实证分析之前，我们首先对相关模型与知识进行介绍。

(1)空间权重矩阵确定

虽然朱平芳等[15]已构造出一种经济距离矩阵，但该矩阵假设只有当空间单元有共同边界时才有经济联系，这种设置方法欠妥。因为当今很多国家之间都有着各种形式的经济贸易，不邻近的空间单元如澳洲、美国等这些发达国家基本上与世界上所有国家都有经济交往。因此，下文构建的空间权重将根据不同空间单元经济变量x的相对差异来构造，并且规定当空间单元即使不相邻，也会存在经济联系。最终确定的权重形式如(1)式所示

(1)

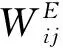
(2)空间/时空相关性大小分析模型

空间相关性大小的分析可通过空间相关系数Moran’s I值进行判断。而分析时空相关性的模型较少，本文运用宋马林等[16]提出的时空相关系数计算模型分析股指的时空相关。

(3)空间面板回归模型

下面采用空间面板计量经济回归模型来分析股指的时空相关作用机理。模型的基本形式如(2)式所示

StockIndexit=αi+ρ(IT⊗W1)StockIndexjt+

β1GDPit+β2M2it+β3CPIit+β4Rit+

β5ExRit+β6Reit+β7Tradeit+θt+ξit

ξit=λ(IT⊗W2)ξjt+εit

εit～N(0,σ2In)i=1,2,…,n,i≠j

(2)

其中StockIndexit股指收益率是一个n×1维向量，其计算公式为第t期股指的收盘价除以第t-1期股指的收盘价。等号右端代表影响股指的7个宏观因素。β是宏观变量的系数，W1和W2均为n×n空间权重矩阵，IT为T×T单位阵。ξjt与εit均为空间干扰项,而αi和θt分别表示个体和时点上的特定效应。ρ为空间滞后相关系数，可度量经济相似一国股指受其他国家股指的影响程度。λ为空间误差相关系数，它反映了经济相似的其他国家股指受一些不可测因素后对某国股指冲击的程度。分块对角矩阵IT⊗W1、IT⊗W2分别为空间面板权重矩阵。当ρ≡0且λ≠0时，模型为空间面板误差模型SPEM(Spatial Error Model)；当ρ≠0且λ≡0时，模型为空间面板滞后模型SPLM(Spatial Lag Model)。

4 实证结果分析与讨论

4.1 空间效应检验与分析

利用空间面板模型(2)作回归分析之前，需先对全局Moran’s I检验来探索性测定各国股指之间是否存在空间相关性。根据检验结果，得知5个阶段各国股指间存在显著的空间相关性。同时可知，虽然样本的空间面板滞后模型(SPLM)和空间面板误差模型(SPEM)的最大似然估计统计量都显著，但是SPLM模型的表现更优，如有更大的似然估计值、模型拟合度更高、空间滞后相关系数也远远大于空间误差系数等。因此，我们选择SPLM模型加以分析，以保证所得出的结论更稳健。

4.2 空间回归结果比较分析

上文对空间相关分析只是探索性的分析，还需通过回归模型进行准确的空间作用机理探究。在4.1节检验结果基础上，进一步需要对SPLM这个模型进行固定/随机效应检验。最后确定建立的模型应采用时间/空间双固定效应。这与以往文献得出固定效应模型更加符合现实的结论一致[17]。模型在5个阶段的估计结果如表2所示。

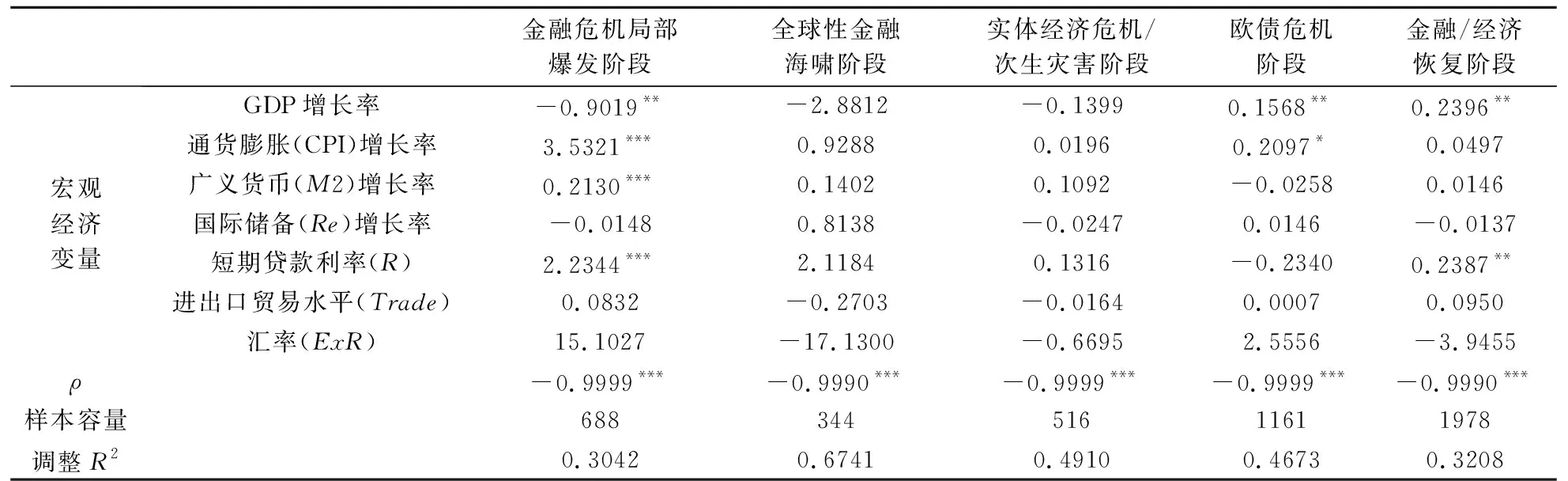
表2 空间面板滞后模型(SPLM)估计结果

注：***、**、*分别表示通过1%、5%、10%下的显著水平检验。

表2可见，5个阶段下GDP增长率、通货膨胀增长率、广义货币增长率及短期贷款利率这四个影响因素中，至少存在一个阶段具有统计学意义的显著性(如在金融危机局部爆发阶段四个因素都显著)。这说明宏观经济因素是股指空间相关传导的共同媒介因素。而国际储备增长率、进出口贸易水平和汇率却在5个阶段下都没有表现出统计显著性，一方面可能与本文数据采集的来源不一致有关，另一方面可能与这几个变量自身对股指影响的复杂性有关。这个研究结论与武占云等[3]的结论基本一致。

另外，在全球性金融海啸阶段及之后的次生灾害阶段，所有的宏观经济变量均未表现出显著性，据此可以推断金融危机阶段，影响股指之间相互作用的因素更加复杂，仅由宏观经济变量不足以解释，可能与中观、微观因素如企业制度、投资者行为或其它随机因素的影响有关。相反，在局部危机阶段或金融相对平稳阶段，如在欧债危机或者金融/经济发展相对平稳阶段，部分宏观经济变量对股指空间自相关影响作用较显著，如GDP增长率在5%显著水平下通过检验。这一结果与很多文献得出的存在经济相似性的国家易受GDP经济增长率的影响的结论一致。假设H2成立。

更为重要的是，在空间面板回归的5个阶段，空间滞后相关系数ρ在所有阶段始终显著。这表明各国股指表现出了显著的空间依赖性。系数为负说明某国股指波动与其经济相似的国家股指的波动反向，不同国家股指之间的相关性主要为负向相关。另外，金融危机阶段的滞后相关系数ρ都大于金融较平稳发展阶段的系数(指的是绝对值)，说明金融危机期间会有更多因素通过传导路径去促进股指空间相关。

4.3 股指空间与时间相关性大小比较分析

以上已从理论模型上论证了股指存在空间相关性。下面将进一步对股指时间/空间相关性大小进行比较分析，定量分析空间相关性在股指联动性方面的作用大小。分析的思路是通过比较时空相关系数及时间序列相关系数的大小，间接知道空间相关性的作用大小。而时空相关系数计算依据为宋马林等[16]研究中的计算公式。限于篇幅，本文仅展示金融/经济逐步恢复阶段部分国家的比较结果(详见表3)，其它结果将用文字表述。

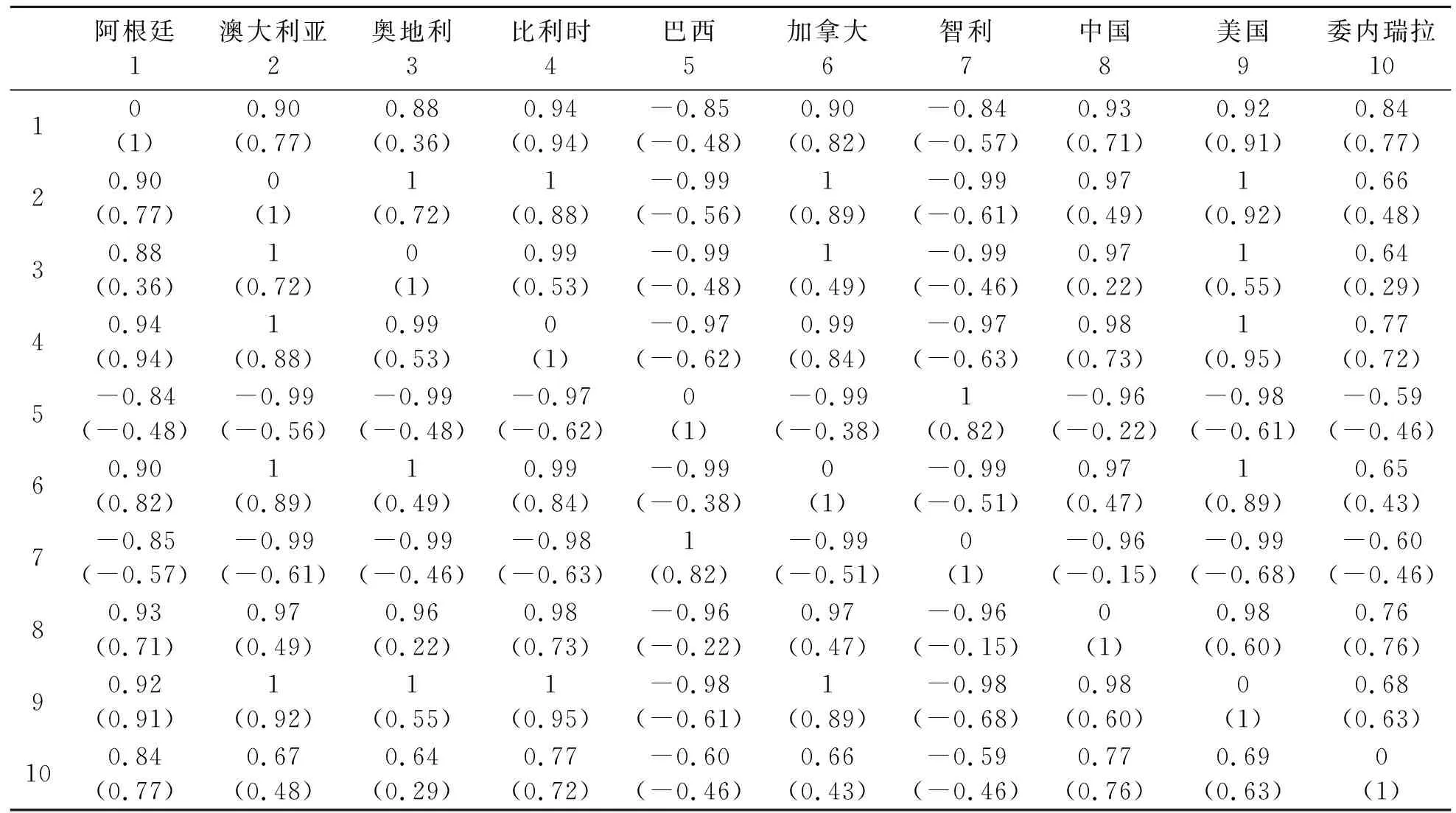
表3 金融/经济逐步恢复阶段时空相关系数与时间序列相关系数大小对比

注：(1)序号1～10依次表示阿根廷、澳大利亚、奥地利、比利时、巴西、加拿大、智利、中国、美国及委内瑞拉。每个国家对应两行数据，第一行代表时空相关系数，第二行代表时间序列相关系数。(2)时空相关系数矩阵中对角线上的数值极小(0)几乎接近于0，且为不对称矩阵；时间序列相关系数矩阵中对角线的值都为1，即自身的相关系数为1，同时矩阵是对称矩阵。这是两种系数的不同规定。

结合表1，可知表3数据涵盖范围不仅包含了发达市场(如澳大利亚与奥地利)股指之间的相关性，也涉及到新兴市场(如中国与巴西)之间股指的相关性，以及发达市场与新兴市场之间(如中国与澳大利亚)的相关性结果，表格列举的数据具有代表性、可信性。另外，在进行两种系数比较之前，首先简单解释表3中数据的特点。表中时空相关矩阵对角线上的数据极小几乎接近于0，这与传统时间序列相关系数矩阵对角线值均为1的规定不同。所以，对两种系数比较时，只需比较非对角线上的数据。可以发现，绝大部分时空相关系数大于时间序列相关系数(绝对值)，较少情况下两者相等(如阿根廷与比利时)。另外，在其它几个阶段，也都可以得出类似的结论，即时空相关系数大于或者等于时间序列相关系数。因此，可以得出空间相关关系在股指相关中占据着重要地位，且相关性大小存在异质性。此外，还可发现，阿根廷与比利时、美国,中国与委内瑞拉等国股指的空间相关性较小。原因可能为阿根廷为新兴市场，与比利时、美国等发达市场在经济运作、经济规模、金融开放条件以及其它制度文化方面等存在较大差距，而使他们之间较少经济往来，这样股指间空间相关性就比较小。现实中，阿根廷长期实行对本国工业进行保护以使其不受外来竞争，但结果却是企业效益增长缓慢；而与此同时比利时、美国等发达国家却是保持着良好经济运作模式及开放条件，从而其经济规模和经济发展速度远远超过阿根廷。这样，阿根廷由于自身的经济、制度方面的原因错失了与比利时、美国等这些发达国家经济来往的机会，股票市场间缺乏交流，而使该国股指与发达市场股指的空间相关性变小。同理，中国与委内瑞拉股票市场虽均为新兴市场，但是两国之间的经济规模、制度文化方面相似性太少，因此二者的股票市场依然缺乏交流，空间相关性较小。可以判定，假设H1成立。

下面进一步分析不同阶段、不同股指之间的相关性大小，及时间、空间相关中哪种类型的相关性起主导作用。考虑到篇幅限制及数据的代表性，本文择取了实体经济危机/次生灾害阶段及金融/经济逐步恢复阶段四个国家(奥地利、中国、美国、委内瑞拉)的两种相关系数数据，绘制成如图1～4所示折线。

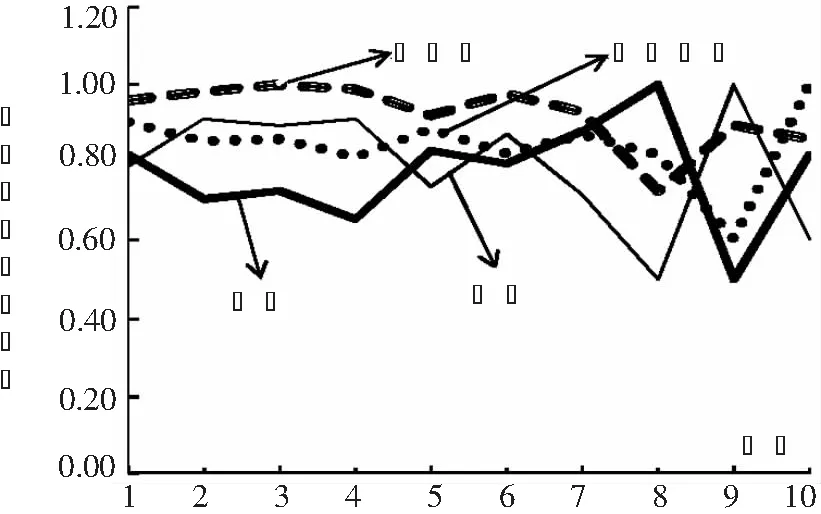
图1 实体经济危机/次生灾害阶段时间序列相关系数

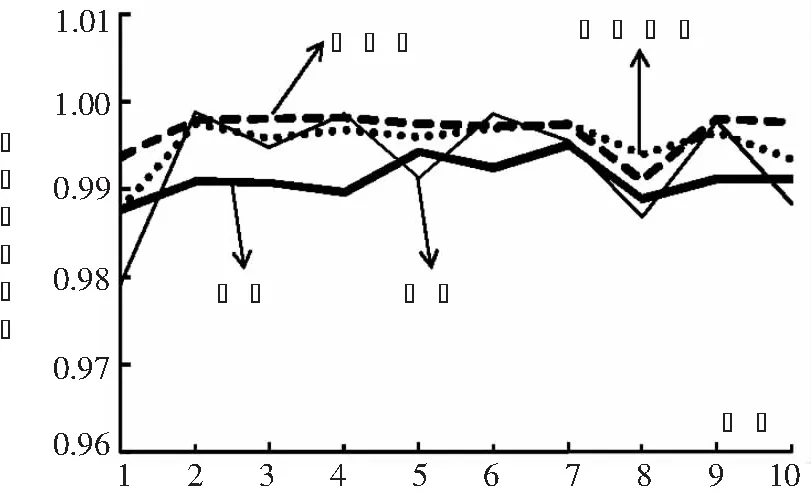
图2 实体经济危机/次生灾害阶段时空相关系数

图3 金融/经济逐步恢复阶段时间序列相关系数

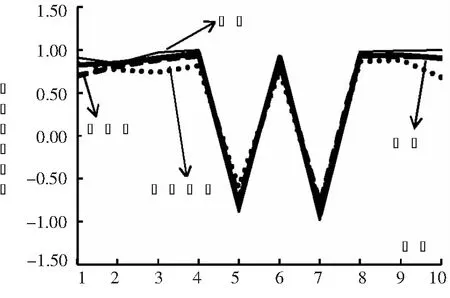
图4 金融/经济逐步恢复阶段时空相关系数

图1表明，在实体经济危机/次生灾害阶段,各国股指之间的时间序列相关系数均较大，无论是新兴市场之间(中国与委内瑞拉)，发达市场之间(美国与奥地利)，还是发达市场与新兴市场之间的股指都呈高度正相关性，这与以往文献[8,11,14]等的研究结论一致。同图1比较，图2同时考虑了时空相关后，其相关系数基本上都大于时间序列相关系数，其中大部分时间序列相关系数在0.60以上。这充分说明在金融危机发生阶段，不论是时间序列相关还是空间相关，各国股指之间均呈现高度相关性，且时间序列相关较大。可以判定，假设H3a成立。

再看图3所示在经济/金融发展相对比较平稳阶段，各国股指之间的时间序列相关性变小，且正、负相关同时存在。发达市场之间的股指基本都呈正相关且相关系数较高(可结合表3所示)，而发达市场与新兴市场，以及新兴市场之间股指相关性则比较复杂，正负相关同时并存且系数大小不一。在图4中，可以清楚地发现，即使是在经济/金融相对和平发展阶段，该阶段的时空相关系数均比同一阶段时间序列相关要大(指的是绝对值)，但每个国家的股指变化大小幅度却不一致。另外，在阶段5，大部分市场的股指之间的相关性仍以时间序列相关为主，但也有极少个别国家以空间相关为主(可结合表3数据所示)，如中国与奥地利、中国与巴西、奥地利与阿根廷等则以空间相关为主。这也再次体现空间相关性呈现异质性特征。该阶段仍然存在大部分股指之间的时间序列相关大于空间相关，再次证明假设H3a成立。

4.4 稳健性测试

(1)空间面板非平稳性检验。由于空间面板模型涉及到经济活动交互效应在时间和空间两个维度进行传递，因此需要对这两个维度的非平稳性进行检验从而排除模型伪回归的可能。而传统的面板模型的非平稳性ADF检验及协整检验不能直接运用于空间面板模型，所以本文借鉴Anselin与Griffith[18]提出的针对空间面板模型平稳性检验方法进行检验。检验结果证明所有样本模型在时间、空间两个维度上均平稳，可以进行空间面板回归分析。

(2)空间相关值检验。空间面板模型最后计算出的值，都比在空间截面计量模型中要小。这说明空间面板模型考虑时间序列相关性后，使股指的空间相关性影响程度降低了。空间面板模型的实质是将模型中股指空间截面之间相关性及时间序列相关性综合考虑，因此检验结果是合理的。换言之，如果仅用空间截面模型或时间序列模型分析股指相关性则是不完备的。

5 结论与建议

通过对43个国家股指的时空相关性进行分析，得到以下结论：

(1)股指之间既存在时间序列相关性，又存在空间相关性，二者共同决定股指的波动。(2)在不同发展阶段，时间序列相关和空间相关表现出不同的特性：在全球性金融海啸阶段及次生灾害阶段，各国股指之间时间/空间相关性均呈现高度正相关，股指之间以时间序列相关为主；而在其它阶段，发达市场股指之间基本呈正相关且相关性比金融危机阶段小；发达/新兴，以及新兴/新兴市场股指之间正负相关同时并存且大小不一。该阶段大部分股指之间仍以时间序列相关为主。(3)考虑时空相关后，大部分股指之间的相关系数达到0.90以上。但也有个别新兴市场与其他国家股指之间相关性较小，约为0.60左右。(4)在全球性金融海啸及次生灾害阶段传统宏观经济变量不能解释空间相关原因。可能该阶段股指空间相关受更多因素影响。

基于以上研究结论，结合马柯维茨投资组合原理，我们建议：(1)投资者应尽可能选择在经济/金融相对平稳发展阶段进行投资。风险厌恶投资者可组合投资于新兴市场与发达市场上，或者全部投资于新兴市场以获得较稳定的收益，这与Driessen和Laeven[19]的结论一致。反之，对于风险偏好投资者，则可投资于相关性较高的发达市场以获得超额收益。(2)由于股指时空相关性会影响股市的收益率，因此需要银行等金融机构在企业以股票进行抵押融资时，需要对贷款价值比率重新进行有效确定。

[1] Fernández-Avilés G, Montero J, Orlov A G. Spatial modeling of stock market comovements[J]. Finance Research Letters, 2012, 9(4): 202-212.

[2] Asgharian H, Hess W, Liu L. A spatial analysis of international stock market linkages[J]. Journal of Banking & Finance, 2013, 37(12): 4738- 4754.

[3] 武占云，魏后凯，王业强.国际金融危机空间传染机制研究——基于空间面板数据的实证分析[J].华中师范大学学报(自然科学版),2014,48(3):418- 424.

[4] Ouyang F Y, Zheng B, Jiang X F. Spatial and temporal structures of four financial markets in Greater China[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 402(2): 236-244.

[5] Tam P S. A spatial-temporal analysis of East Asian equity market linkages[J]. Journal of Comparative Economics, 2014, 42(2): 304-327.

[6] Tobler W. Global spatial analysis[J]. Computers, Environment and Urban Systems, 2002, 26(6): 493-500.

[7] 邸倩,蒋海.金融危机国际传导机制的空间计量分析[J].南方金融,2011,(10):9-13.

[8] 贾颖,杨天化.“次贷危机”下发达国家和地区股票指数的惯性效应与反转效应——以美国、日本、欧洲、香港为例[J].金融研究,2011,(8):157-166.

[9] 周林洁.公司治理、机构持股与股价同步性[J].金融研究,2014,(8):146-161.

[10] 林宇,李川,贺莹.不同市场态势下东亚股市联动结构变化研究[J].投资研究,2014,(9):116-134.

[11] Albulescu C T, Goyeau D, Tiwari A K. Contagion and dynamic correlation of the main European stock index futures markets: a time-frequency approach[J]. Procedia Economics and Finance, 2015, 20: 19-27.

[12] Dimic N, Kiviaho J, Piljak V, et al.. Impact of financial market uncertainty and macroeconomic factors on stock-bond correlation in emerging markets[J]. Research in International Business and Finance, 2016, 36: 41-51.

[13] 董杰,潘和平,姚一永,等.基于DCC-MV-GARCH模型的石油、股票和黄金市场相关性实证研究[J].预测,2012,31(4):53-57.

[14] Gong P, Weng Y L. Value-at-Risk forecasts by a spatiotemporal model in Chinese stock market[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 441: 173-191.

[15] 朱平芳,张征宇,姜国麟.FDI与环境规制:基于地方分权视角的实证研究[J].经济研究,2011,(6):133-145.

[16] 宋马林,王舒鸿,汝慧萍.一种新的考虑时间和空间的相关系数及其算例[J].数量经济技术经济研究,2010,(7):142-152.

[17] Baltagi B H, Georges B, Pirotte A. Fixed effects, random effects or Hausman—Taylor?: a pretest estimator[J]. Economics Letters, 2003, 79(3): 361-369.

[18] Anselin L, Griffith D A. Do spatial effects really matter in regression analysis[J]. Papers in Regional Science, 1988, 65(1): 11-34.

[19] Driessen J, Laeven L. International portfolio diversification benefits: cross-country evidence from a local perspective[J]. Journal of Banking & Finance, 2007, 31(6): 1693-1712.