盘式制动器制动噪声分析
钟颖强,杨 晋
(江西交通职业技术学院,江西 南昌 330013)
0 引言
“截至2014年年底,我国机动车保有量为2.64亿辆,其中汽车保有量达1.54亿辆”。汽车保有量的剧增给人们带来便利的同时也严重危害我们的日常生活与工作,据有关部门统计,城市噪声污染中交通运输噪声可占75%,且汽车噪声则占其中的85%。尤其是车辆制动时产生的制动噪声,其频率一般在1 kHz~16 kHz之间,声压在65 dB~90 dB之间,最大值甚至达到110 dB[1]。制动噪声不仅损害车辆的舒适性与交通环境的和谐,还危害人们的身心健康。并且制动噪声问题会造成汽车厂与零部件厂的直接经济损失,损害它们的品牌形象,影响它们的长远发展。2002年著名咨询公司J.D.Power的调查报告显示,在汽车用户对制动器的投诉中,有60%以上归咎于制动时的尖叫[2]。摩擦材料生产商每年50%以上的资金也被用于解决相关问题[3],北美地区每年大约有10亿美元被用于解决制动器振动与噪声问题[4]。被美国《消费者杂志》多次评为“最佳中型SUV”,且被美国高速公路安全局授予5星安全认证的新款汉兰达,由于刹车时有撞击声,就引发许多客户抱怨,甚至遭受客户投诉。近年来,低阻尼耐高温新材料取代石棉作摩擦衬片、以及汽车结构的轻量化趋势使得制动噪声问题更加突出,成为迫切需要解决的问题[5]。
由于制动振动与噪声是一个复杂的非线性动力学问题,其产生的工况复杂多变,且具有随机性,噪声再现及问题捕捉试验特性统计难度较大,所以,制动噪声仍是当今汽车工业的老大难问题。目前人们一般采用理论分析法、有限元法、试验等方法对制动噪声问题进行多层次、多角度的研究,其中有限元方法具有研究周期短、研究成本低等优势而成为研究制动噪声必不可少的手段。复特征值分析方法[6]能够充分考虑制动器各部件的结构耦合特性与摩擦特性,分析结果符合工程技术要求,是目前进行制动噪声分析最普遍、通用的方法。
本文采用有限元法中的复特征值分析对盘-块简化模型进行研究,提取系统方程的复特征值,利用复特征值的实部和虚部来判断制动噪声的频率和发生倾向。
1 制动系统的复特征值理论
建立制动系统的数学模型进行振动分析,有助于我们更深刻更直观地了解噪声机理。有阻尼制动系统的自由振动方程为:

(1)
其中:[M]、[C]、[K]分别为系统的质量矩阵、阻尼矩阵、刚度矩阵;{X}为振动位移。汽车制动时,制动力垂直作用于制动块,使制动块与制动盘间产生摩擦阻力,达到减速制动系统引入摩擦力时的振动方程为:
(2)
其中:{Ff}为摩擦力。通常认为Ff是线性[7],即:
{Ff}=[Kf]{X}.
(3)
其中:[Kf]为摩擦刚度矩阵。将式(3)代入式(2)可得:
(4)
如式(4)所示,摩擦力导致的系统刚度耦合,系统刚度矩阵不对称,特征矩阵不对称,求解出的特征值有些是复数,即系统各阶模态频率和模态振型都是复数,如下式:
X=Ψest.
(5)
其中:Ψ为特征向量;s为特征值。将式(5)代入式(4)得:
(s2[M]+s[C]+[K-Kf])Ψ={0}.
(6)
对式(6)求解可得特征值和特征向量。系统第i阶特征值为:
si=αi+jβi.
(7)
其中:αi为实部,即为系统的不稳定系数;βi为虚部,即为系统的自然频率(或者系统不稳定频率)。
对系统振动方程解耦,得到阻尼比小于-0.01的能激发出制动摩擦噪声的不稳定频率与不稳定系数[8],预测制动时振动噪声的发生,具有可靠合理性与普遍实用性。文献[9]通过复特征值分析得出:减小摩擦因数、增大制动盘刚度、使用阻尼材料的制动背板和改变摩擦片的形状都会减小制动尖叫。吕辉、于德介等[10-11]将响应面法与有限元复特征值技术相结合,提出了一种随机参数汽车制动器系统稳定性的分析方法,分析准确地得到了随机参数正态分布假设下系统特征值的概率统计特性和参数灵敏度,提出修改制动器支撑背板的厚度可有效改善制动器系统的稳定性,减小制动噪声的产生。
2 各零件的自由模态有限元分析
2.1 有限元模型的建立
在三维软件UG中建立研究的制动器简化模型,模型包含通风式制动盘、制动块(含摩擦衬块底板、摩擦衬块背板、摩擦衬块)、制动支架三大主要部件,导入有限元分析软件ABAQUS中建立仿真模型。有限元模型的建立采用了文献[6]中的假设,为了保证计算精度,采用3 mm~5 mm的网格尺寸,网格主要为六面体单元,类型为C3D8,且应尽量保持制动块与制动盘接触面的网格一致,参考通用的网格处理标准完成网格划分,如图1所示。各部件的材料参数根据厂家提供的数据以及GB5763—2008《汽车用制动器衬片》做线性材料替代处理,其值见表1。
2.2 各零件的自由模态有限元分析
模态分析研究结构在某一易受影响的频率范围内的各阶主要模态的振动特性,预测结构在此频段内在外部或内部各种振源作用下产生的实际振动响应,为设备的振动噪声诊断和结构的优化设计提供依据[12]。制动器主要部件的自由模态分析广泛地被运用于制动振动噪声分析中,文献[13]研究了部件的模态特征参数与制动振动噪声的关系,为制动器结构的减振降噪设计与研究奠定基础。

图1 简化的制动器有限元模型

部件密度(kg/m3)弹性模量(GPa)泊松比制动盘7 3001270.3摩擦衬块2 7004.30.3摩擦衬块背板7 8202070.29摩擦衬块底板7 2001750.28制动支架7 2001750.28
3 锤击试验
为了更好地研究制动器的振动噪声,对制动器的制动盘、制动片、制动支架三大主要部件进行了固有频率的锤击试验,如图2所示,得到的结果如表2所示。
由表2可知,对比各零件的固有频率锤击试验结果与自由模态有限元分析结果,其相对误差范围在5%以内,满足分析精度要求,表明制动器的简化有限元模型可靠有效。

图2 锤击模态试验

部件频率阶次12345678910制动盘试验得到频率(Hz)9932 4502 8563 3504 1094 4705 3557 3487 5927 620仿真得到频率(Hz)1 0022 4522 8893 2684 0274 5325 5617 0577 3177 414误差(%)-0.9-0.0-1.12.451.98-1.39-3.853.973.632.70制动片试验得到频率(Hz)1 6572 7093 9304 8125 8036 0926 4527 8508 2768 983仿真得到频率(Hz)1 6402 8134 1354 6995 7056 1716 6057 5878 1439 026误差(%)1.03-3.83-5.22.351.69-1.30-2.373.351.61-0.48制动支架试验得到频率(Hz)1 9652 0472 2563 1033 6383 8106 4757 6778 5199 377仿真得到频率(Hz)1 9262 1222 1923 1673 7453 8776 3117 3728 8869 774误差(%)1.98-3.62.84-2.0-2.94-1.762.533.97-4.31-4.23
4 制动器制动尖叫台架试验验证
在ABAQUS软件中进行有限元模型的复特征值分析,并开展制动器的制动噪声的台架试验,有限元模型的复特征值分析和制动噪声的台架试验都得到各自计算结果,即不稳定模态(复模态)。
试验与仿真的分析工况:①拖滞制动工况,转速为5 rad/s;②制动压力为5 MPa;③摩擦因数为0.3。
复特征值分析得到的结果与制动噪声的台架试验测得的不稳定频率对比如图3所示。
结果表明:仿真分析结果存在部分的欠预测(如2.2 kHz)和过预测(如7.1 kHz、7.5 kHz、8.6 kHz),这是由于制动噪声本身的复杂性及不可重复性等因素,但大致的复特征值模态分析结果与台架试验结果有很好的一致性,验证了简化的有限元模型的正确合理性。
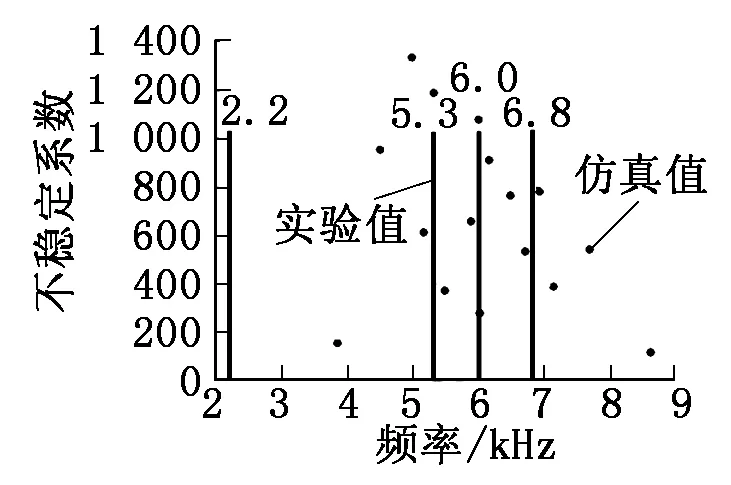
图3 制动噪声试验与仿真的复模态对比
5 结语
本文探讨了制动振动噪声的研究方法,并基于简化的盘式制动器的三维模型建立有限元模型,进行了制动盘、制动块、制动支架的自由模态分析和系统的复特征值分析,并开展固有频率锤击试验和制动噪声台架试验。通过自由模态仿真分析和锤击试验结果对比,其误差均在5%以内,验证了有限元模型的可靠性。由制动噪声试验和复特征值分析得到的不稳定模态频率及振型图分析可知,制动时产生的系统不稳定性是诱发制动噪声的关键因素。
参考文献:
[1] 吕红明, 孟德建, 张立军,等.基于盘/销装置的摩擦尖叫噪声研究[J].振动、测试与诊断,2014,34(1):46-51.
[2] Yang M,Blaschke P,Afaneh A H.A study of disc brake high frequency squeal and disc in-plane/out-of-plane modes[J].SAE Paper,2003-01-1621.
[3] Jones D I G.Reflections on damping technology at the end of the twentieth century[J].Journal of Sound & Vibration,1996,190(3):449-462.
[4] 国家自然科学基金委员会工程与材料科学部.机械工程学科发展战略报告(2011-2020)[R].北京:科学出版社,2010.
[5] Singh R,Sheikh A A,Mitchell M J.Viscoelastic damping to control disc brake squeal[J].Journal of Sound and Vibration,1998,32(10):18-22.
[6] 庞明,张立军,孟德建,等.鼓式制动器摩擦尖叫的复模态模型与影响因素研究[J].振动与冲击,2014(8):35-41.
[7] Júnior M T,Gerges S N Y,Jordan R.Analysis of brake squeal noise using the finite element method:A parametric study[J].Applied Acoustics,2008,119(5):147-162.
[8] Guan Di-hua,Jiang Dong-ying.A study on disc brake squeal using finite element methods[J].SAE Paper,980597.
[9] Liu P,Zheng H,Cai C,et al.Analysis of disc brake squeal using the complex eigenvalue method[J].Applied Acoustics, 2007,68(6):603-615.
[10] 吕辉,于德介.随机参数汽车盘式制动器的稳定性分析[J].振动工程学报,2014(5):647-653.
[11] 吕辉,于德介,陈宁,等.引入不确定参数的汽车盘式制动器振动稳定性分析[J].振动工程学报,2014,27(6):900-906.
[12] Kinkaid N M,O′Reilly O M,Papadopoulos P.Automotive disc brake squeal[J].Journal of Sound & Vibration,2003,267(1):105-166.
[13] 张立军,唐传骏,庞明,等.制动盘弹性模量对制动尖叫影响的仿真分析[J].汽车工程学报,2013(5):313-323.

