基于粗糙遗传BP神经网络的滚动轴承故障诊断*

唐立力

(重庆工商大学融智学院，重庆 401320)

0 引言

滚动轴承是机械装置中非常重要的零件，滚动轴承故障一旦发生将导致整个机械设备出现严重事故，从而导致严重的经济损失或人员伤亡[1],因此，实现滚动轴承故障的有效诊断显得极其重要。BP神经网络用于滚动轴承故障诊断的效果较好[2]，但是BP算法的主要缺陷为易形成局部极小而得不到全局最优，学习效率低，收敛速度慢。为了实现取长补短、优势互补、获取更优的诊断性能，将BP神经网络与其他智能方法结合起来进行故障诊断研究就成为了一种趋势[3-7]。粗糙集、遗传算法和BP神经网络的融合在诸多方面得到了应用[8-10]，本文利用美国凯斯西储大学的轴承数据来验证模型，提出基于粗糙遗传BP神经网络的滚动轴承故障诊断方法。首先利用粗糙集理论来约简决策表的条件属性，简化了BP网络结构；然后利用遗传算法来寻求BP网络初始权值和阈值的最优解，克服了常规BP网络固有的缺陷，减少了遗传算法的寻优迭代次数，提高了诊断精确度。

1 滚动轴承特征参数提取

本文的研究中选用美国凯斯西储大学的滚动轴承数据，选取功率谱熵、小波熵、盒维数、关联维数、峭度和偏度作为滚动轴承故障判断的特征向量[11]。将这6个参数作为网络输入向量，BP神经网络待识别的轴承故障位置定义为内圈损伤、外圈损伤、滚动体损伤和正常轴承4种模式。

2 初始BP神经网络故障诊断模型

初始BP神经网络模型的构建根据故障诊断系统输入输出数据特点确定，采用非线性映射能力强的3层网络，由于故障特征输入向量有6维，因此BP网络输入层有6个节点。隐含层节点数根据柯尔莫哥诺夫定理确定[12]：

H=2R+1.

(1)

其中：H为隐含层节点数；R为输入层节点数。取R=6，计算得：H=13。

待诊断的故障位置类型共有4类，现对故障类型进行编码，用(1 0 0 0) 表示正常轴承，用(0 1 0 0)表示内圈损伤，用(0 0 1 0)表示外圈损伤，用(0 0 0 1)表示滚动体损伤，得到输出层有4个节点。

3 RS-GA-BP神经网络故障诊断模型

融合粗糙集理论(RS，Rough Sets)[13]、遗传算法(GA，Genetic Algorithm)[14]和BP神经网络的故障诊断模型主要分解为粗糙集与BP网络集成、遗传算法与BP网络集成两个部分，如图1所示。

4 仿真与分析

本文利用美国凯斯西储大学的滚动轴承数据来验证RS-GA-BP神经网络故障诊断模型的有效性。轴承选用SKF6205-2RS深沟球轴承，12 kHz的采样频率，对轴承的故障位置进行诊断，包括正常轴承、损伤直径为0.54 mm的内圈损伤、外圈损伤、滚动体损伤4种状态。对这4种状态进行编码后，所得编码定义为BP网络的目标输出，经特征提取得到部分训练样本和测试样本。对其进行归一化[15]处理的变换式如下：

(2)

其中：xi为网络输入数据；xmin为网络输入数据的最小值；xmax为网络输入数据的最大值，归一化后样本数据如表1、表2所示。

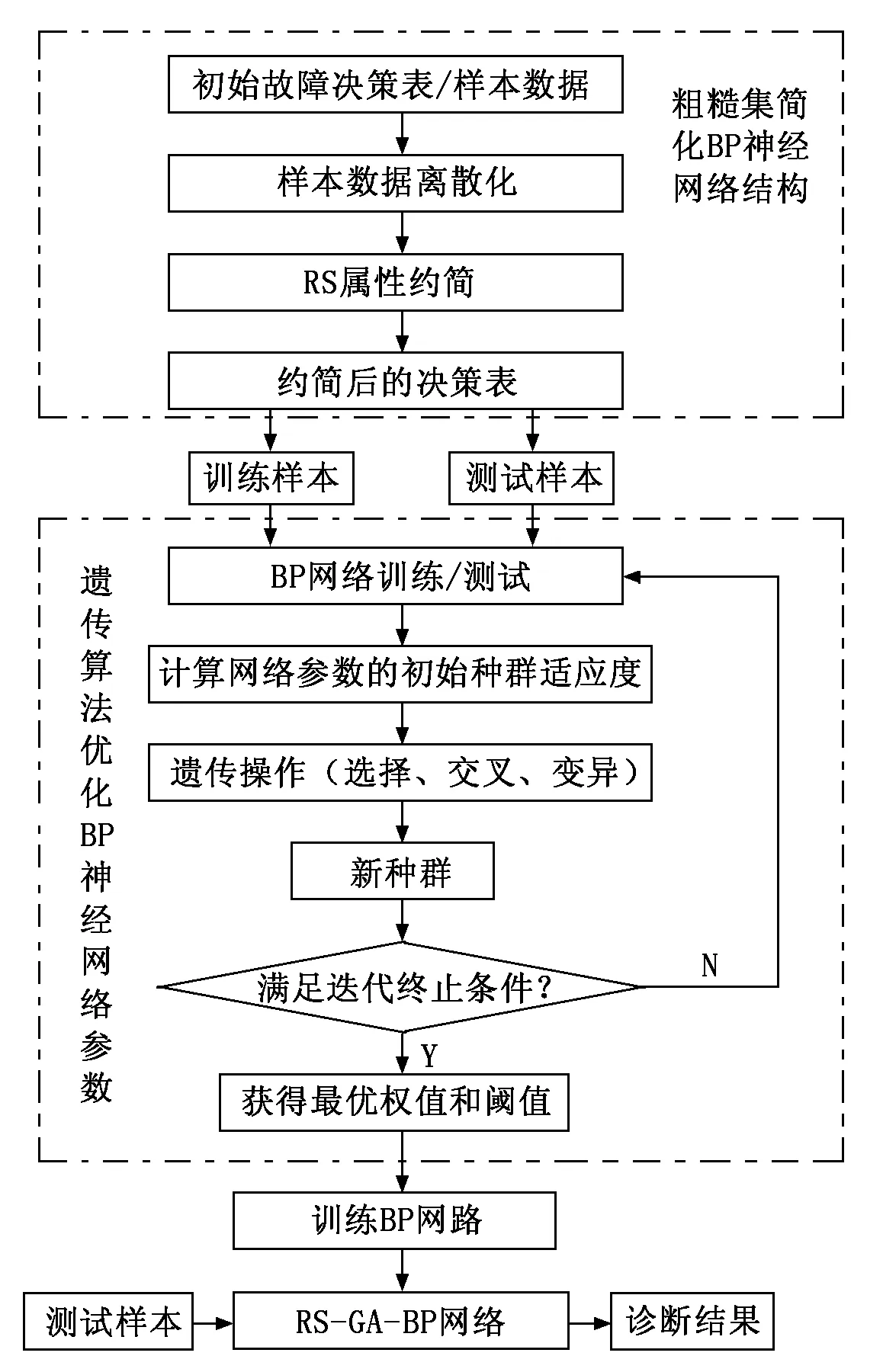
图1 RS-GA-BP神经网络故障诊断模型

(1) 数据离散化。对表1中的训练样本采用等频率划分算法[16]进行离散化，将条件属性值划分为3个区间，利用Rosetta软件实现样本数据离散化。

(2) 条件属性约简。 采用可辨识矩阵约简方法[17]去约简决策表的条件属性，通过Rosetta软件提供的遗传算法来实现训练样本约简过程，得到小波熵、关联维数、峭度作为约简后的条件属性，测试样本也作同样的约简。

(3) BP神经网络结构和参数确定。通过分析确定BP、GA-BP、RS-BP、RS-GA-BP这4种网络的结构分别为6-13-4型、6-13-4型、3-7-4型、3-7-4型。隐含层的传递函数设置为tansig，输出层的传递函数设置为logsig，训练算法设置为trainlm，性能函数选用mse，训练目标设置为0.01。

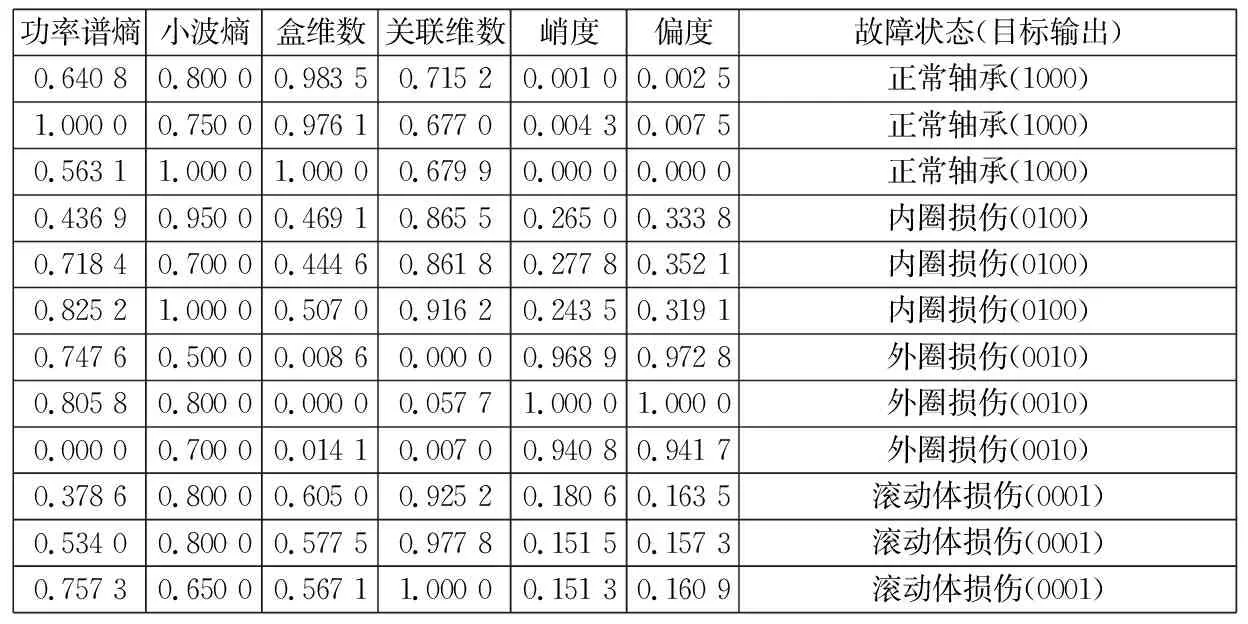
表1 部分训练样本(决策表)

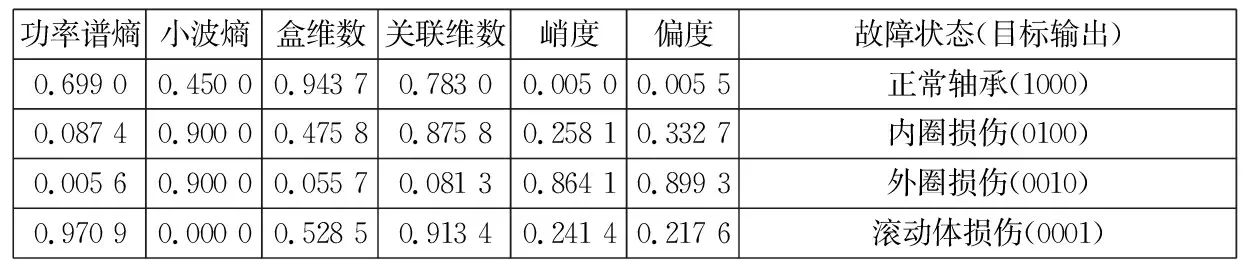
表2 测试样本

(4) 遗传算法的参数设置。个体采用二进制编码且位数为10，适应度函数选用排序的适应度分配函数，选用随机遍历抽样作为选择算子，选用单点交叉作为交叉算子、交叉概率设置为0.7，选用离散变异作为变异算子、变异概率设置为0.01，种群大小设置为40，最大遗传代数设置为50，代沟设置为0.95。

(5) 网络误差进化过程分析。在MATLAB R2013a软件上对GA-BP网络和RS-GA-BP网络分别进行仿真，得到均方误差的进化曲线，如图2、图3所示。由图2、图3的进化结果看出，相比GA-BP网络，RS-GA-BP网络的误差变化有一定的下降，遗传寻优迭代次数由38减少到11。

(6) 网络优化前后的仿真分析。用训练样本分别对BP网络、GA-BP网络、RS-BP网络、RS-GA-BP网络进行训练，得到各自训练误差曲线，如图4、图5、图6、图7所示。对比图4和图7看出，常规BP网络达到训练目标超过了7步，而RS-GA-BP网络达到训练目标不足7步，克服了BP网络收敛速度慢的缺陷。

图2 GA-BP误差进化曲线 图3 RS-GA-BP误差进化曲线 图4 BP网络训练误差曲线

用测试样本分别对BP网络、GA-BP网络、RS-BP网络、RS-GA-BP网络进行仿真，得到的RS-GA-BP网络故障诊断结果如表3所示。结合4条训练误差曲线，得到的4种网络仿真结果对比如表4所示。从表3可以看出，RS-GA-BP网络的诊断结果正确。从表4可以看出，RS-GA-BP网络比常规BP、GA-BP、RS-BP三种网络的训练和测试误差更小，克服了常规BP网络陷入局部极小的缺陷，改善了训练效果，提高了故障诊断精度。

5 结束语

本文将粗糙集理论和遗传BP神经网络进行有效融合，提出一种新的滚动轴承故障诊断方法。仿真结果表明，该方法简化了BP网络结构、降低了BP网络计算量、克服了常规BP网络收敛速度慢、容易陷入局部极小点问题，减少了遗传算法寻优迭代次数，相比常用的3种智能诊断模型提高了诊断效率和精度。该方法还可以推广到其他类机械设备的故障诊断中。

图5 GA-BP网络训练误差曲线 图6 RS-BP网络训练误差曲线 图7 RS-GA-BP网络训练误差曲线

表3 RS-GA-BP网络故障诊断结果

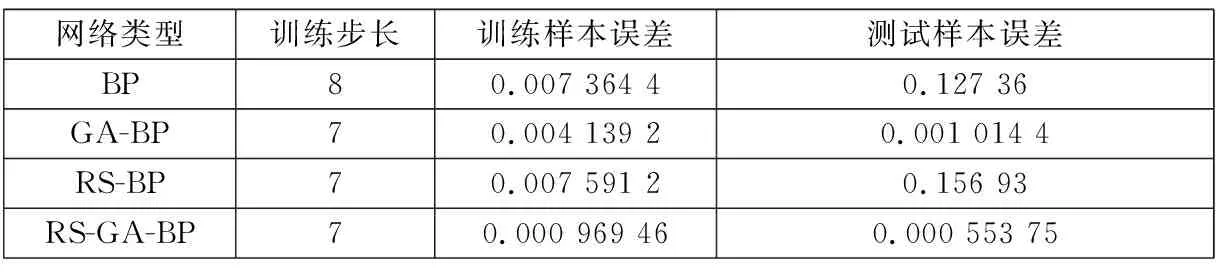
表4 4种网络仿真结果对比

参考文献：

[1] 阳建宏,黎敏,丁福焰.滚动轴承诊断现场使用技术[M].北京:机械工业出版社，2015:1-5.

[2] 方进,龚珺,刘良峰,等.基于BP神经网络的滚动轴承智能诊断技术[J].安徽师范大学学报(自然科学版),2016,39(2):103-108.

[3] 王宇,魏秀业.基于混合蛙跳优化神经网络的轴承故障诊断研究[J].机械传动,2017,41(5):127-131.

[4] 陈法法,陈保家,程珩,等.运用免疫遗传算法优化WNN诊断滚动轴承早期故障[J].噪声与振动控制, 2016,36(6):158-163.

[5] 候一民,孙嘉兵,张宇,等.基于PSO-BP神经网络和Hilbert谱奇异值的滚动轴承故障诊断[J].组合机床与自动化加工技术,2014(7):77-83.

[6] Muhammet Unal,Mustafa Onat,Mustafa Demetgul,et al.Fault diagnosis of rolling bearings using a genetic algorithm optimized neural network[J].Measurement,2014，58:187-196.

[7] 程加堂,艾莉,熊伟.基于蚁群神经网络的滚动轴承故障诊断[J].轴承,2012(2):34-36.

[8] 董晓雷,贾进章,樊程程,等.粗糙集—改进神经网络落煤瓦斯涌出量预测[J].辽宁工程技术大学学报(自然科学版),2014,33(5):587-591.

[9] 胡平,彭纪奎.粗糙集—传神经网络在挖掘机故障诊断中的应用研究[J].微电子学与计算机,2011,28(3):55-58.

[10] 肖河,肖盛.基于粗糙集理论的遗传神经网络风速预测模型[J].电网与清洁能源,2012,28(9):82-87.

[11] 徐强,刘永前,田德,等.基于萤火虫群算法优化最小二乘支持向量回归机的滚动轴承故障诊断[J].振动与冲击,2014,33(10):8-12.

[12] 王红君,刘冬生,岳有军.基于小波分析和神经网络的电机故障诊断方法研究[J].现代电子技术,2010(20):147-149.

[13] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社，2001.

[14] 雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社，2014.

[15] 韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社，2011.

[16] 张钰莎,蒋盛益.连续属性离散化算法研究综述[J].计算机应用与软件,2014,31(8):6-8.

[17] 张小红,裴道武,代建华.模糊数学与Rough集理论[M].北京:清华大学出版社，2013.