基于数据场和水平集演化的图像分割
陈乔松,冉会琼,闫亚星,刘 晓,周冰玉,卢大强,董师周,王 进,邓 欣
(重庆邮电大学 计算机科学与技术学院 计算智能重庆市重点实验室,重庆 400065)
0 引 言
图像分割是图像预处理中的一个重要环节,图像分割指的是根据灰度、颜色、纹理、形状等特征把图像分为互不交叠的区域,使得这些特征在同一区域内呈现出相似性和一致性,而在不同区域间呈现出明显的差异性。将图像的不同区域分割开来,即是将目标从背景中分割开来,便于后续的研究所用。图像分割的效果直接影响到后续对图像的分析和处理结果,因此,图像分割成为图像处理的热点问题之一。
近年来,在大量研究者的努力下,不同的分割方法相继出现。总体来说,可以将图像分割方法划分为以下几种:基于阈值的分割方法[1]、基于边缘的分割方法(如sober,canny等)、基于区域的分割方法、基于图论的分割方法、基于能量泛函的分割方法[2-4]和其他类型的分割方法。其中,基于阈值的分割方法是最基本也是最广泛的一种分割方法,其基本思想是根据图像的灰度特征,设定一个或者多个阈值作为分割临界值,来区分图像不同的区域,得到图像的目标和背景。如果仅使用图像灰度特征,而忽略图像的空间结构信息,会使基于阈值的图像分割方法存在局限性;基于边缘的分割方法,主要根据图像分割的定义,区域内和区域间所持有的特性,基于图像边缘处的灰度值阶跃性以及对应一阶导数极值和函数的二阶导数过零点这一特性,可以使用微分算子进行边缘检测;基于区域的分割方法,主要是将图像按照对应的相似性准则分成不同的区域,这类方法主要有种子区域增长法、区域分裂合并法和分水岭算法,但是该类方法对图像噪声较为敏感;基于图论的分割方法,主要是采用图论的思想,将图分为若干子图,子图之间保持相似度最小,子图内部保持相似性最大,该类方法主要有GraphCut[5],GrabCut[6]和Random Walk等,该类算法效率较低。基于能量泛函的分割方法,主要是根据能量函数的不断更新和演化,不断确定边缘所在,这类方法主要指的是活动轮廓模型,分为参数活动轮廓模型和几何活动轮廓模型。
综述以上分析,本文采用最广泛的阈值分割方法,充分考虑图像像素间的相互作用,引入Michael Faraday提出的数据场理论。场的概念是从物理学的角度引申而来,相信相互不接触的粒子之间,仍然靠着某种不可见的转换媒体相互联系。李德毅、王树良等[7-8]提出数据场,认为粒子在物理空间与数据空间之间相互转换,在数据空间内的所有对象均存在相互作用,每个粒子既产生能量,也接收能量。根据数据场的这个概念可以发现,将数据场应用到图像上的也能够充分表示图像的空间结构信息,将数据场的这个优点应用到图像上,有效地构建图像空间上联系,保留图像的空间结构信息。将数据场的思想应用到图像上的算法主要有基于数据场的聚类算法[8-10]、基于数据场和PCA的人脸识别算法[11]、基于数据场的图像分割算法[12-17]等。
在采用数据场的图像分割方法中,主要是根据图像势值信息,按照可视化方法或者利用过渡区域来确定最优阈值,实现最终阈值分割。本文根据图像势值信息,获取对应的势值等势线,采用势值等势线信息来确定最终的分割结果。此外,为完善阈值分割结果,本文利用基于能量泛函的演化方式来细化边缘区域。能量泛函主要以基于水平集的方法应用最为广泛,水平集的基本思想是将低维空间嵌入到高一维的空间中,该方法能够有效处理曲线的拓扑结构变化,有效地分割出图像的不同区域,基于水平集的图像分割有大量的研究成果。
在上述背景下,本文提出一种基于数据场和水平集演化的图像分割方法,该方法结合数据场的思想,将图像从灰度值空间转换到数据场的势空间,根据势空间的势值分布信息得到相应势值等势线分布;根据势值等势线的分布情况,采用自适应阈值化分割方法,得到对应的二值化分割结果。此外,根据水平集边缘曲线演化的方法,把得到的图像二值化结果作为水平集初始演化曲线,根据能量泛函不断更新图像边缘曲线。
1 基于数据场和水平集的图像分割
1.1 算法流程
本文考虑到细节会影响边缘的探测和处理,因此,对图像进行平滑预处理。本文主要采用局部极值插值的方式对图像进行平滑,得到图像的基础层;利用数据场保存图像信息间的相互关系;采用自适应阈值的分割方法对图像进行分割。为使得到的结果更精确,引入水平集曲线演化的思想,将结果进一步完善得到最终分割结果。整个算法步骤如下。
步骤1输入待分割图像,进行平滑预处理,得到平滑图像;
步骤2对平滑后的图像采用数据场求解图像势值分布;
步骤3对得到的图像势值分布图,求解自适应阈值,对图像进行自适应分割;
步骤4得到的二值化图像进行水平集曲线演化;
步骤5输出二值化结果和曲线演化结果。
1.2 基于局部极值插值的边缘保持预处理
对于图像分割而言,主要是为了得到图像的目标区域。因此,图像分割不需要保留图像细节部分,从而考虑将图像细节部分进行平滑,在保证图像边缘信息不丢失的情况下有效平滑图像细节部分。
能够去除图像细节信息并且有效保留图像边缘信息,在文献[18]中采用基于局部极值的边缘保持的多尺度图像分解方法充分做到了这一点。首先将图像定义为基础层和细节层,如(1)式。
I=Idetail+Ibase
(1)
(1)式中:Idetail表示细节层图像;Ibase表示基础层图像。
基于局部极值插值的边缘保持算法主要包括以下3个步骤。
①定义图像I的局部极大值和局部极小值;
②分别对局部极大值和极小值做插值,计算对应的最大和最小极值信封;
③通过得到的最大和最小极值信封,计算平滑图像M。
对于图像的多尺度分解部分,主要表示为不同尺度下所对应的细节图像和平滑图像的和,其表达式为
(2)
(2)式中:Di表示在不同尺度下所对应的细节图像;Mn表示最终的平滑图像。
1.3 基于数据场的图像势值分布
数据场是模拟物理空间场的方法学,描述在整个空间中对象与对象间的相互作用。从数据场对应的概念可以看出,对于图像空间而言,能够有效表示图像空间像素间的相互关系,保留图像的全局和局部信息,克服了传统的图像分割只对图像灰度信息进行处理的局限性。
将数据场引入到图像处理中,将图像的各个像素点作为一个对象,对象间的相互作用关系构成数据场。对于图像空间p中的某个对象q,对象q在某点像素p所产生的势值的数学表达式为
(3)
(3)式中:σ表示影响因子,控制数据对象的影响范围;‖p-q‖表示2点之间的距离;mq表示对象q的质量。因此,在影响因子的控制下,对于整个图像空间p内的任一点对象x的势值计算式为
(4)
(4)式中:‖x-y‖≤σ表示对象x满足2个对象间的距离在σ范围内。
根据(4)式可得整个图像对应的图像数据场的势值分布结果。这个结果能够体现图像像素点间的相互关系,有效保留图像的全局和局部信息。根据图像势值分布图,将势值相等的部分连接起来从而形成等势线,等势线能够从一定角度反应图像的架构和整体布局。将数据场的思想应用到图像上进行处理,得到的结果如图1所示。图1中的横、纵坐标分别表示图像的宽度和高度,单位是像素。

图1 图像势值等势线Fig.1 Equipotential lines of image
从图像数据场对应的等势线情况可以分析,不同的势值间存在不等的区域,不同的区域间必然存在差异性。图像分割就是尽可能地将同质区域划分出来,使各个区域内部保持最大的相似性,不同的区域间的差异性较大。根据图像分割这样的特性,分析等势线的形成以及等势线之间存在的差异,可以根据势值间区域大小得到分割阈值所对应势值范围。
1.4 自适应阈值分割
在图像分割中,阈值分割使用最为广泛,其中主要有大津法、最小误差法和最大熵法。本文主要利用数据场所持有的特性,能够有效地保留图像的空间结构信息,且考虑对于图像边缘存在区,图像灰度值的一阶导数存在极值,二阶导数过零点。根据数据场的思想可以有效保留图像空间信息,并且能够得到势值等势线,从而考虑将这个思想应用到势值等势线上,将图像势值变化区域较大的部分视为边缘所在的区域。
对得到的势值等势线图像,不同区域的势值变化较大,同一区域的势值变化较小,从而在不同区域的势值等势线之间,所包含的数据对象也较多,所呈现的势值变化也越大。不同势值之间所包含的数据对象变化为
ΔZi=ΔZi+1-ΔZi
(5)
(5)式中:i=1,2, … ,n-1;Zi表示第i个势值;ΔZi表示对应第i的势值与第i+1的势值间的数据对象所对应的梯度变换值, 即在势值i与势值i+1间所包含的数据对象个数。对得到的势值变换梯度值进行排序,根据(6)式能够得到所对应的变化幅值,如图2所示。

图2 势值变换数值排序Fig.2 Sort of the potential value
(6)
(6)式中:i=1,2, … ,n-2;ΔL表示排序后相邻区域间,数据对象所对应的数据增量。从图像分割的性质分析可知,当ΔL最大时,即为图像边缘所在的区间。因为当ΔL最大时,表示在所对应的区间上阶级跳跃较大。为使得分割阈值更加精确,不断更新阈值所在的区间,即重新选择当ΔL最大时对应的区间作为待分割阈值区间。在重新确定的阈值分割区间上重复(5)式和(6)式,不断地更新对应的待分割阈值区间。一直重复更新到阈值分割区间变得足够小为止,最后取该区间最大和最小势值的均值作为分割阈值。
1.5 水平集曲线演化
对于得到的阈值分割结果,虽然能够较好地得到二值化分割结果,但是对于部分边缘并不能很好地分割出来。水平集演化,能够在能量函数的驱动下实现曲线的拓扑演化,能够得到更好的边缘曲线,更逼近边缘所在的区域。
在文献[3]中,为避免重新初始化水平集函数带来的问题,对能量泛函进行重新定义,如
ε(φ)=uRp(φ)+λLg(φ)+alg(φ)
(7)
(7)式中:Rp(φ)表示距离正则化项;Lg(φ)+lg(φ)表示外部能量项,μ,λ,α均为常量,表示对能量函数变化的约束。为得到图像变化较为稳定的区域,采用梯度流最小化能量函数。
在文献[3]中对图像边缘的检测,所使用的边缘检测函数为
g
(8)
(8)式中:Gσ表示标准差为σ的高斯核函数,通过高斯函数对图像I进行卷积得到平滑图像结果,然后再对平滑图像求梯度,根据梯度变化来确定当前曲线的运动,当越接近对象边缘的时候,对应的g值也越来越小。
在该文提出的算法中,所使用的边缘检测函数不采用平滑后的图像,而是采用拉普拉斯锐化后的拉普拉斯图像,因为该方法能够使图像边缘与其他部分存在更大的差异性,从而也能更容易确定边缘所在并进行快速收敛。所以,在该文提出的算法中最终所使用的边缘检测函数为
g
(9)
(9)式中,GL表示采用使用L的滤波器模板,通过该边缘检测函数与图像I卷积得到平滑结果,使用该函数能够使演化曲线更精确的停留在目标边缘处。
本文采用水平集演化不需要人为设定初始分割曲线,而是根据自适应阈值得到的结果作为初始演化水平集函数,有效地利用了自适应分割结果。
2 实验结果与分析
2.1 实验环境
本文实验均在MATLAB上实现,其中,实验图像包括合成图像和自然场景的彩色图像;合成图像中部分图像是带有噪声的,自然场景的彩色图像主要以BSDS500数据库的图像为主,该数据库包含500张自然场景内的图片,包括300张训练图片和200张测试图片,图3显示了部分合成图像和部分BSDS500数据库图像。

图3 合成图像和自然图像(BSDS500)Fig.3 Synthesis and natural image
为了定量的比较分割结果,本文用正确率、和误分率作为决策准则。
1)计算正确率。
F=2PR/(P+R)
(10)
(10)式中:F表示正确率;P表示算法分割区域与人工标注分割目标共有像素占算法分割区域总像素的百分比;R表示实际分割区域与人工分割区域的共有像素占总像素的百分比。
2)计算误分率。
(11)
(11)式中:ME表示误分率;Bo和Fo分别表示参考图像的背景和目标;Bt和Ft分别表示实际分割图像的背景和目标;Bo∩Bt表示正确分割的背景像素集合;Fo∩Ft表示正确分割的目标像素集合。
2.2 实验结果
根据本文提出的算法,我们采用基于局部极值插值的方法对图像进行平滑预处理,该方法在进行平滑的同时能够有效保留边缘信息,从而降低图像细节信息对分割结果的影响。图4为使用局部极值插值算法进行平滑与不使用局部极值插值算法分别对应的效果图。
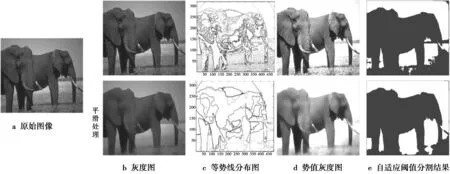
图4 采用平滑的效果对比Fig.4 Comparative effects smoothing
从图4可以得到,相比较原始灰度图,采用局部极值插值的灰度图中,大象身上的细节部分被忽略以及大象的整个边缘信息有效地保留,同时,草坪上的细节部分也被平滑,进而整个图像在没有细节信息的干扰下能够得到更锐利的边界信息。再者,灰度图对应的势值等势线验证了大象的主要边缘信息得到保留。最后,图4e所对应的自适应分割效果显示平滑后能够减轻细节信息对分割结果的干扰。综上,采用本文中提出的自适应阈值方法可以有效地分割出主要的边缘区域。
为了显示本文所提出的方法的有效性,在同一实验环境和实验数据下与现有的关于数据场的图像分割算法进行对比,其中,有通过得到的图像数据场来比较图像势值,从而推导出图像对应的过渡区域,根据图像过渡区域来计算阈值的data field-based transition region extraction and thresholding[15],通过设定2个不同的质量函数得到图像的相对数据场和绝对数据场,通过设定合适的阈值得到图像的高、低灰度区集合,将高、低灰度区看成2类样本采用逆向云发生器算法得到图像背景和目标的云模型表示,根据图像像素的隶属度程度来得到最终分割结果的利用云模型和数据场的图像分割方法[16]。
图5显示了在合成图像和自然分割图像上的分割结果,分别采用的是合成图像七边形、双目标和BSDS500数据库的自然图像花坛、小鸟、熊和大象来实现本文算法并且在同样的实验环境下实现文献[15]和文献[16]2个算法的结果,并对结果做出相应的分析和讨论。

图5 合成图像和自然图像的分割结果Fig.5 Segmentation results of the synthesis image and the BSDS500 database
为了更直观地表示算法的有效性,表1、表2分别表示了实验结果的正确率和误分率。

表1 实验结果的正确率
2.3 结果分析
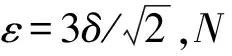
对以上的实验结果进行分析,对合成图像,本文提出的算法能够有较好的实验结果,对于噪声图像也进行了有效的处理,算法具有实用性。从实验结果发现,文献[15]分割方法对于噪声图像的分割结果并不理想,对于无噪声图像能够得到较好的分割结果。而文献[16]的分割方法在分割结果上则较为不理想,不能有效处理噪声在实验中带来的影响。

表2 实验结果的误分率
对自然图像的分割结果进行分析可以发现,本文提出的方法能够更有效地分割出目标,能够较好地处理细节部分对分割结果的影响。文献[15]得到的分割结果对于图像细节部分进行有效地保留,能够较好地体现出图像边缘的过渡细节,但是在图像分割中,往往只需要保留图像目标,而对于细节部分可以进行恰当的处理。而文献[16]不能得到较好的结果,不能有效地将目标区域完整的区分出来。
从表1、表2数据可以看出,本文算法在大多数实验结果中均表现出了更好的分割结果。其中,文献[16]在七边形和双目标上表现出较低的正确率和较高的误分率,主要是因为噪声的影响。
以上的结果分析发现,提出的方法无论是针对合成图像还是自然图像,均能保留较好的边缘信息,能够更完整地得到图像目标区域,对于噪声图像本文提出的方法仍具有鲁棒性能。
2.4 演化实验结果和分析
二值化分割结果表明部分边缘细节不能很好地区分,为更完善图像目标区域,本文加入水平集曲线边缘演化来完善目标边缘区域。将阈值分割得到的二值化结果作为水平集曲线演化的初始演化目标函数,对部分未能准确定位边缘的结果进行演化,从而能够得到更好的分割结果。图6显示了演化后的实验结果。

图6 边缘演化结果Fig.6 Results of the evolution of the edge
从图6可以看出,对于小鸟阈值分割的二值化结果进行演化,能够将小鸟所在的区域完整的显示出来。大象二值化结果没有很好地将大象鼻子区域区分,采用边缘演化得到结果可以将大象鼻子区域很好地呈现出来,也将大象边缘轮廓更加完善。
从水平集演化上来看,将初始化轮廓最大限度的提取出来,可以有效减少曲线演化次数。
3 总 结
本文提出了一种基于数据场和水平集演化的图像分割算法。本文通过采用局部极值插值的方法对图像进行了平滑处理,只取基础层来进行下一步的图像分析,避免图像细节信息对图像分割结果的干扰。数据场从物理世界的短程辐射核场得到启发,根据数据场的概念生成图像数据场及其对应的势值,从而能够有效地表示图像间的相互关系,有效利用势值进行自适应分割。将本文提出的算法和已存在的利用数据场的图像分割算法作对比,在合成图像和自然图像上进行对比实验,实验结果显示,提出的算法具有更好的分割结果。此外,为使得到更好的边缘,本文采用基于拉普拉斯的边缘检测函数进行曲线边缘演化。
参考文献:
[1] MEDEIROS R S, SCHARCANSKI J, WONG A. Image segmentation via multi-scale stochastic regional texture appearance models[J]. Computer Vision & Image Understanding, 2016, 142(C): 23-36.
[2] JIANG Xiaoliang, WANG Qiang, HE Biao, et al. Robust level set image segmentation algorithm using local correntropy-based fuzzy c-means clustering with spatial constraints[J]. Neurocomputing, 2016, 207(C): 22-35.
[3] LI Chunming, XU Chenyang. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254.
[4] LI Chunming, XU Chenyang, GUI Changfeng, et al. Level set evolution without re-initialization: a new variational formulation[C]//In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington: IEEE Press, 2005: 430-436.
[5] VICENTE S, KOLMOGOROV V, ROTHER C. Graph cut based image segmentation with connectivity priors[C]//In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE Press, 2008: 1-8.
[6] ROTHER C, KOLMOGOROV V, BLAKE A. “GrabCut”: interactive foreground extraction using iterated graph cuts[C]//In Proceedings of the ACM Transactions on Graphics. New York: ACM Press, 2004: 309-314.
[7] 李德毅, 刘常昱, 杜鹢,等. 不确定性人工智能[M]. 北京: 国防工业出版社, 2014: 193-217.
LI Deyi, LIU Changyu, DU Yi, et al. Artificial intelligence with uncertainty[M]. Beijing: National Defence Industry Press, 2014: 193-217.
[8] LI Deren, WANG Shuliang, GAN Wenyan, et al. Data field for hierarchical clustering[J]. International Journal of Data Warehousing & Mining, 2011, 7(4): 43-63.
[9] WANG Shuliang, CHEN Yasen. HASTA: a hierarchical-grid clustering algorithm with data field[J]. International Journal of Data Warehousing & Mining, 2014, 10(2): 39-54.
[10] WANG Shuliang, WANG Dakui. ELMDF: a new classification algorithm based on data field[C] //In Proceedings of the 2014 IEEE International Conference on Bioinformatics and Biomedicine.Belfast:IEEE Press,2014:28-33.
[11] WANG Dakui, LI Dongwei, LIN Yi. A new method of face recognition with data field and PCA[C]//In Proceedings of the 2013 IEEE International Conference on Granular Computing.China:IEEE Press,2013:320-325.
[12] WU Tao. Image data field-based framework for image thresholding[J]. Optics & Laser Technology, 2014, 62(10): 1-11.
[13] 陈露, 秦昆, 杨海全,等. 基于数据场的图像分割方法初探[J]. 地理空间信息, 2007, 5(6): 79-81.
CHEN Lu, QIN Kun, YANG Haiquan, et al. Image segmentation based on data field[J]. Geospatial Information, 2007, 5(6): 79-81.
[14] 吴涛, 秦昆, 区磊海,等. 图像二维阈值分割的数据场方法[J]. 华南理工大学学报:自然科学版, 2010, 38(11): 128-134.
WU Tao, QIN Kun, QU Leihai, et al. Data field-based method for image segmentation with two-dimension threshold[J]. Journal of South China University of Technology: Natural Science Edition, 2010, 38(11): 128-134.
[15] WU Tao, QIN Kun. Data field-based transition region extraction and thresholding[J]. Optics & Lasers in Engineering, 2012, 50(2): 131-139.
[16] 吴涛, 秦昆. 利用云模型和数据场的图像分割方法[J]. 模式识别与人工智能, 2012, 25(3): 397-405.
WU Tao, QIN Kun. Image segmentation using cloud model and data field[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(3): 397-405.
[17] WU Tao, QIN Kun. Image data field for homogeneous region based segmentation[J]. Computers & Electrical Engineering, 2012, 38(2): 459-470.
[18] SUBR K, SOLER C, DURAND F. Edge-preserving multiscale image decomposition based on local extrema[J]. Acm Transactions on Graphics, 2009, 28(5): 89-97.

