高速卫星通信系统中的盲均衡算法研究
李昂阳,杜 伟,方天琪
(1.北京理工大学 信息与电子学院,北京 100081;2.中国电子科技集团公司第二十八研究所,南京 210007)
0 引 言
在高速卫星通信系统中,符号速率非常高,群延时抖动的影响会变得很大,再加上信道的衰落等其他原因,接收到的码元会存在很严重的码间串扰,从而造成错误判决[1]。为了解决这一问题,我们引入均衡技术来对信道失真进行补偿[2-3]。
由于卫星信道具有时变性和随机性,这就要求我们能实时地跟踪信道变化,调整滤波器抽头系数,也就是采取自适应技术来补偿信道特性[4]。自适应均衡主要分为2类:传统自适应均衡和盲均衡。一般传统自适应均衡器需要一个训练序列。这种技术固然提高了可靠性,但也存在着一些制约。信道的选择性衰落和多径传输会使得接收机无法跟踪信道变化,甚至导致通信中断。在某些特定的应用场景下,接收机不可能得到学习序列。比如信息截获或侦查系统等。学习序列的插入会占用数据传输时间,极大地降低了通信效率,因此不适用于高速卫星通信系统。
盲均衡可以不借助学习序列的帮助,只是采用接收机所接收到的原始信号,便能够对卫星通信信道的不平坦和抖动进行均衡[5]。
本文给出了恒模算法、改进的恒模算法和多模算法3种自适应盲均衡算法。针对高速卫星通信中的多种调制方式,从工程的角度选择了不同的盲均衡算法,来完成硬件实现。经过仿真验证,在使用最少硬件资源的前提下,盲均衡算法取得了良好的均衡效果,有效地降低了通信系统误码率[6]。
1 均衡的基本概述

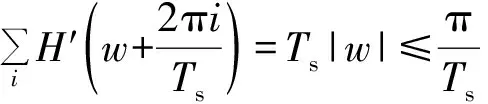
信号经过信道传输后,进入接收机,在接收滤波器和抽样判决器之间插入一个均衡器。故需要一种性能优异的自适应均衡算法,使这个均衡器能够自动地更新滤波器的抽头系数,实现自适应的功能。
2 3种盲均衡算法
盲均衡算法有很多,其中最容易完成硬件实现的是基于Bussgang技术的盲均衡算法,特别是对其进行符号简化后可大大减少硬件资源消耗,故这种算法被广泛应用于ASIC和FPGA的设计中。
2.1 恒模算法
在现存的基于随机梯度的盲均衡自适应算法中,广泛应用的是恒模算法(constant modulus algorith,CMA)[7-9]。均衡器原理框图如图1所示。图1中,s(n)为发送符号数据,可表示为s(n)=a(n)+jb(n),其中,a(n)和b(n)分别为其实部和虚部;H(n)是信道冲激响应;v(n)是加性高斯白噪声;Wn为均衡器抽头系数。

图1 均衡器原理框图Fig.1 Equalizer schematic block diagram
令接收信号矢量Yn=[y(n),y(n-1),…,y(n-N+1)]T,N为均衡器横向滤波器抽头数;均衡器抽头系数矢量W=[w(0),w(1),…,w(n-1)] 。基于随机梯度算法的自适应均衡器系数的迭代形式为

(1)
(1)式中:μ是迭代步长;J(w)是代价函数;en是误差项,并与均衡器输入信号Yn及迭代步长共同构成误差校正项。
而对于CMA算法,它的代价函数能够描绘为[10]
J(w)=E{[|z(n)|2-R2]2}2
(2)
(2)式中,R是一个仅仅和信源统计特性相关的恒定正常数。CMA算法的误差项为
en=z(n)[|z(n)|2-R2]
(3)
针对16QAM调制方式,CMA算法的均衡原理,如图2所示。CMA算法是通过调整调制信号星座点的幅值,将之收敛成一个固定的值来达到消除码间串扰的目的。它只和信号的幅值相关,所以,不会因为信号频偏和相偏的影响而导致均衡出错,但是在迭代进行过程中,由于有限字长等因素的影响,也有可能人为的引入相偏,因此,CMA算法应在载波同步之前完成[11]。
2.2 改进的恒模算法
由于CMA算法只考虑到信号的幅度,对相位没有考虑,所以均衡器收敛后,由于信道的非线性特性和载波偏移的缘故,输出信号会产生一个随机相位,从而导致稳态误差变大。为了克服这一缺点,文献[12]提出了一种改进的恒模算法(modified constant modulus algorithm,MCMA)。

图2 CMA算法均衡原理图Fig.2 CMA algorithm equalization schematic diagram
针对16QAM调制方式,MCMA算法的均衡原理如图3所示。

图3 MCMA算法均衡原理图Fig.3 MCMA algorithm equalization schematic diagram
对于一个二维的系统,将代价函数修改成实部加虚部的形式,即
J(k)=JR(k)+JI(k)
(4)
(4)式中,JR(k)和JI(k)分别对应着均衡器输出y(k)=yR(k)+jyI(k)的实部和虚部,并且有
JR(k)=E[(|yR(k)|2-RR)2]
(5)
JI(k)=E[(|yI(k)|2-RI)2]
(6)
假设输入数据a(k)=aR(k)+jaI(k)是独立同分布的随机变量,RR和RI是分别由aR(k)和aI(k)决定的常实数,则有
(7)
(8)
此时的误差函数e(k)=eR(k)+jeI(k) 由(9)—(10)式给出
eR(k)=yR(k)(|yR(k)|2-RR)
(9)
eI(k)=yI(k)(|yI(k)|2-RI)
(10)
相对于CMA算法来说,MCMA算法同时考虑到了信号的幅度信息和相位旋转。可是,针对不同半径上的星座点来说,MCMA算法还是没有根据半径的不同,设置不同的均衡坐标,从而导致,MCMA算法在稳态剩余误差和误码率方面的提升不是很明显[13]。
所以,我们又针对不同半径圆上的星座点,提出了多模算法(multi-modulus algorithm,MMA)。
2.3 多模算法
多模算法是将高阶调制信号划分在多个判决点上来进行均衡。对于16QAM调制方式,其均衡原理如图4所示[14]。
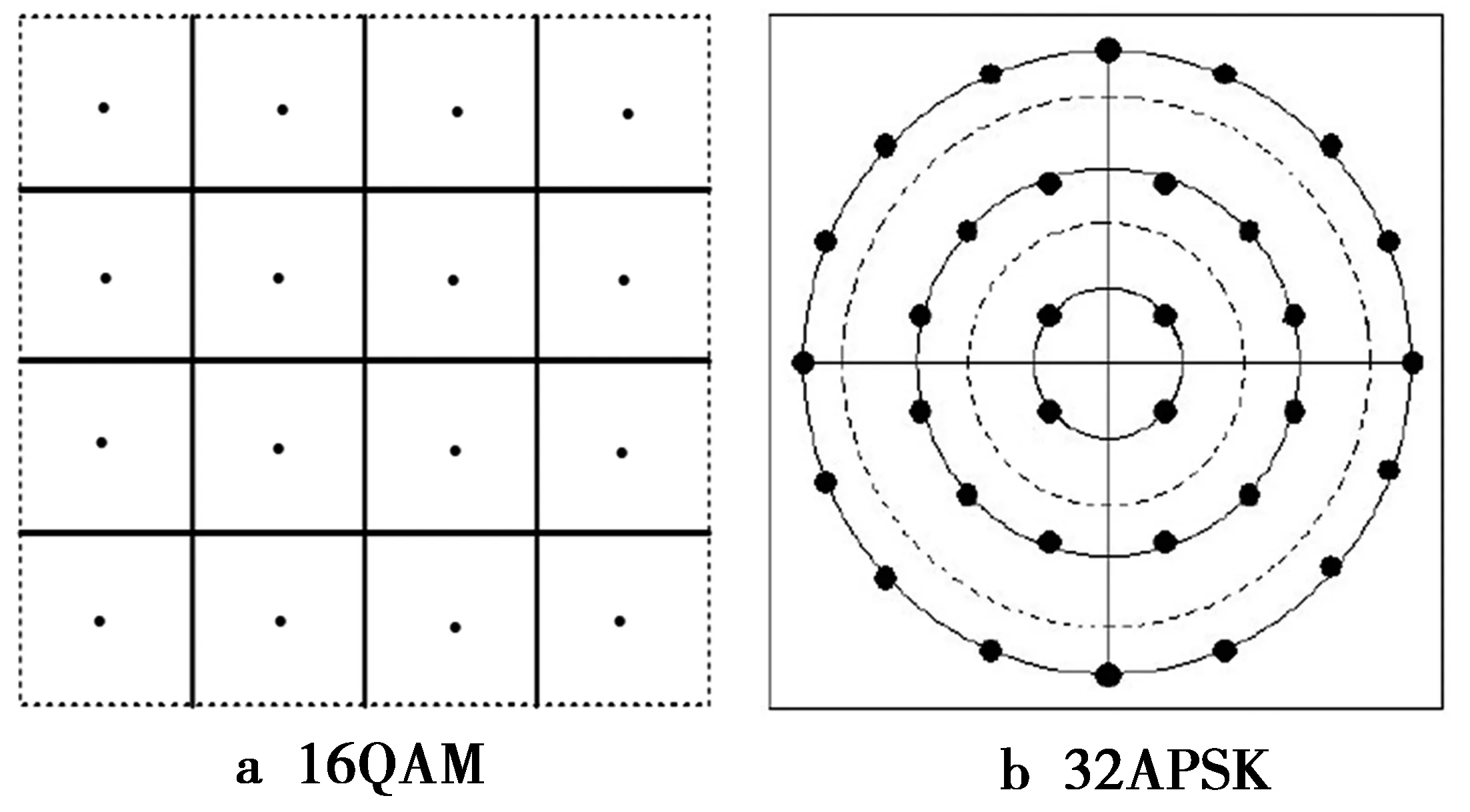
图4 MMA算法均衡原理图Fig.4 MMA algorithm equalization schematic diagram
图4中,先对每一个输入的信号星座点进行判决,然后将它均衡到距离判决星座点最近的一个星座点上。阈值判决装置中存在已知调制方式星座点的位置坐标,然后对输入的每一个调制信号进行判决。判决方法是计算它的位置坐标和每一个理想星座点位置之间的距离,然后根据距离的大小,选择出和它距离最近的调制星座点,然后将该调制星座点的坐标作为判决装置的输出,我们将这种算法称为基于点判决域的多模算法[15]。
上述这种算法的代价函数为
(11)
(11)式中,zR(n)为均衡器输出信号z(n)的实部,zI(n)为均衡器输出信号z(n)的虚部。即
zR(n)=real(z(n))
(12)
zI(n)=imag(z(n))
(13)
MMA算法的误差函数为
(14)
从(11)—(14)式,我们可以看出,MMA算法将信号的实部和虚部分开处理并使输出信号的实部和虚部分别向与它最接近的星座点的实部、虚部靠近,该算法不仅考虑了信号的相位信息,可以克服卫星通信信道的不理想特性以及载波偏移导致的相位失真,而且还考虑了落在不同半径上的不同星座点幅值的不同,因此,相对于CMA算法而言,提高了幅值的精度。
在实际应用中由于频偏的存在,所以,32APSK调制星座图为三圈,而不是明显的星座点,故基于点判决的MMA算法不适用。将算法改进一下,采用判断幅值的方法,32APSK星座图如图4所示。将32APSK星座图设置2个门限,第1个门限设置在内圈和中圈之间,第2个门限设置在中圈和外圈之间。如果滤波器模块输出信号幅值小于第1个门限,则误差信号为滤波器模块输出信号模的平方与内圈星座点幅值平方之差;如果滤波器模块输出信号幅值大于第1个门限小于第2个门限,则误差信号为滤波器模块输出信号模的平方与中圈星座点幅值平方之差;如果滤波器模块输出信号幅值大于第2个门限,则误差信号为滤波器模块输出信号模的平方与外圈星座点幅值平方之差。
此时代价函数与CMA算法类似,只是这时J(w)=E{[|z(n)|2-R2]2}中R值不再是固定的一个值,而是取自3个根据统计特性算出来的值,先判决滤波器输出处于哪个区域,再与相对应的R值平方相减,得出误差信号。
3 性能分析
3.1 星座图分析
分别利用CMA,MCMA,MMA这3种均衡算法对采用8PSK,16APSK,32APSK和64APSK这4种调制方式的通信系统进行了均衡仿真,其星座图对比如图5所示。

图5 CMA,MCMA和MMA均衡前后星座图对比Fig.5 Comparison of constellation before and after CMA, MCMA and MMA
从图5可以看出,单从均衡效果上来讲,针对8PSK,16APSK,32APSK和64APSK这4种调制方式,采用MMA算法的效果最优,MCMA算法其次,最后是CMA算法。
但是从均衡的速度和算法的难度来看,正好相反。CMA算法就是单纯的将所有输入信号均衡到一个半径已知的圆上。MCMA是分别将输入信号的实部和虚部均衡到固定的横、纵坐标。而MMA算法是要先对所有的输入信号进行点判决域判决,所以,速度会变慢,难度也相应增加。
8PSK,16APSK和32APSK的星座图分别分布在1个、2个、3个圆上。CMA,MCMA和MMA 3种算法对这3种调制方式的均衡效果相当,由于CMA算法均衡速度最快,实现复杂度最低。所以,针对这3种调制方式,可以选择CMA算法来完成均衡的硬件实现。
然而针对64APSK的调制方式,其星座点分布在4个圆上。可以看出,CMA和MCMA算法对64APSK的均衡效果很差,只有MMA算法对64APSK有良好的均衡效果。所以,针对64APSK这种调制方式,为了取得良好的均衡效果,可以选择MMA算法来完成均衡的硬件实现。
3.2 稳态剩余误差分析
图6给出了在4种不同调制方式下,CMA,MCMA和MMA算法收敛后的剩余稳态误差。由图6可见,CMA算法的收敛速度较快,在大约50次迭代更新后,均衡就进入了一个相对稳定的状态,均衡误差也开始平稳;8PSK,16APSK,32APSK,64APSK的均方误差依次增大。MCMA算法在大概进行100次迭代后,其均方误差达到了稳定,虽然相对CMA算法来说,均衡速度要稍慢一些,但是这样的均衡速度还是接受的。从均方误差的值上来看,和CMA算法的均方误差相比较,MCMA算法的均方误差要稍小一些,但是减小的幅度有限。MMA算法的均衡速度相对较慢,但是MMA的稳态均方误差相对CMA算法和MCMA算法来说,减小很多。
3.3 误码率分析
图7给出了CMA,MCMA和MMA 3种算法在16APSK调制方式下均衡前后的误码率对比图。由图7可见,MCMA算法和MMA算法的误码率性能稍优于CMA算法,3种算法的误码率性能相差不大。

图6 收敛后的稳态剩余误差Fig.6 Steady residual error after convergence
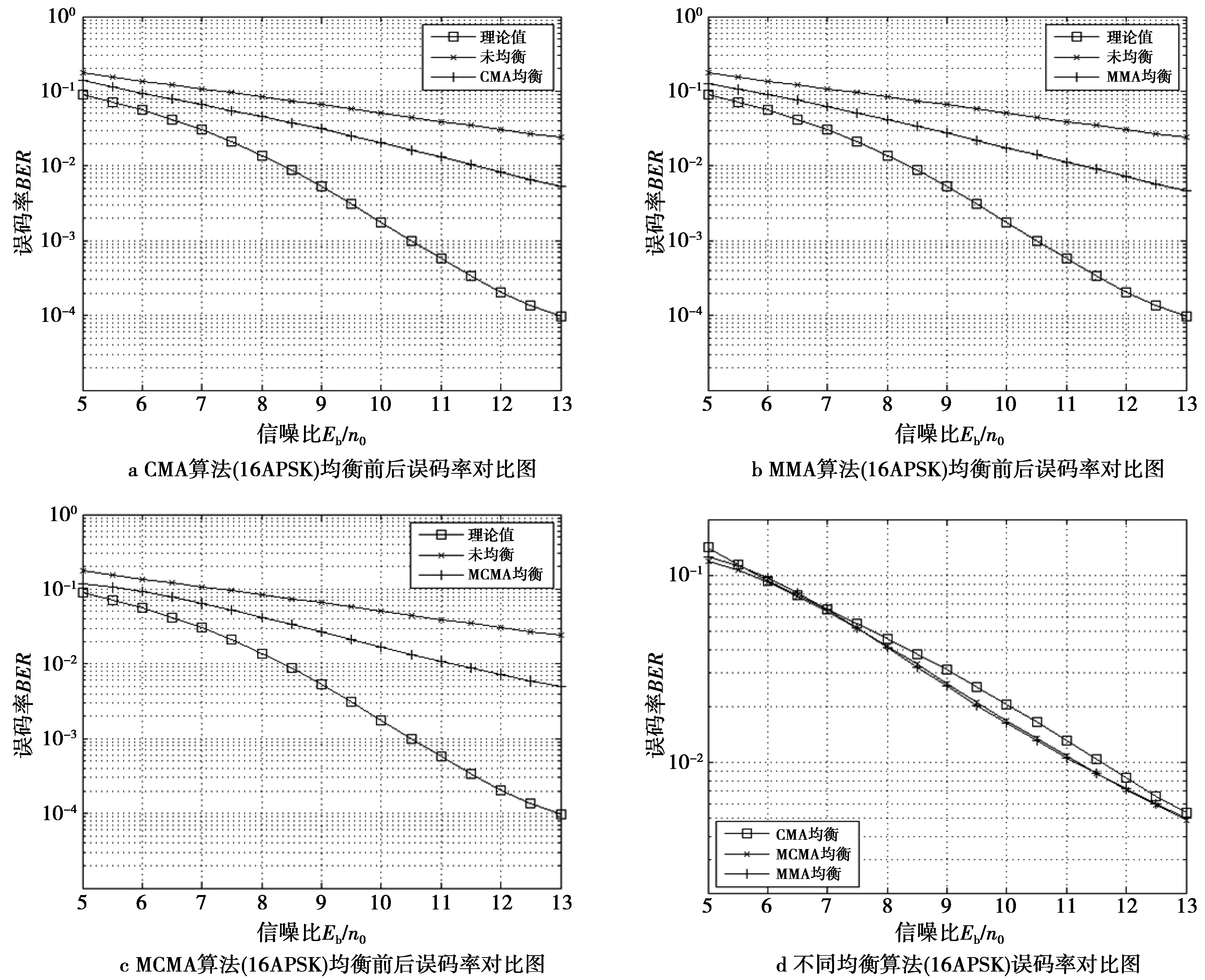
图7 CMA,MCMA,MMA 3种算法的16APSK均衡前后误码率对比Fig.7 Comparison of BER before and after with CMA, MCMA and MMA for 16APSK
4 结 论
1)在高速卫星通信系统中,针对不同的调制方式,应选择不同的盲均衡算法。从工程的角度考虑,在保证均衡效果的前提下,应选择复杂度最低,速度最快的算法,
2)采用自适应盲均衡技术可以有效地对信道失真进行补偿,减小码间串扰带来的影响,降低误码率,提高通信系统接收性能。
参考文献:
[1] 饶伟,高惠娟,段美怡,等. 一种新的基于复指数函数映射的盲均衡算法[J]. 电子学报, 2016, 44(5):1009-1016.
RAO Wei,GAO Huijuan,DUAN Meiyi,et al. New blind equalization algorithm based on a mapping from a complex exponential function[J]. Acta Electronica Sinica,2016, 44(5):1009-1016.
[2] VANKA R N,MURTY S B, MOULI B C. Performance comparison of supervised and unsupervised/blind equalization algorithms for QAM transmitted constellations[C]//IEEE. International Conference on Signal Processing and Integrated Networks. Noida,India: IEEE Press, 2014:316-321.
[3] 饶伟.多径衰落环境中具有调制识别能力的盲均衡新算法[J].电子学报,2013,41(7):1284-1289.
RAO Wei. New blind equalization algorithm with ability of modulation classification under the condition of multipath propagation [J]. Acta Electronica Sinica,2013(07):1284-1289.
[4] 魏武,左天虎,刘期烈,等.卫星通信中一种改进的变步长LMS均衡算法研究[J].重庆邮电大学学报:自然科学版,2014, 26(1):42-48.
WEI Hu,ZUO Tianhu,LIU Qilie,et al. A modified variable step size LMS adaptive filtering algorithm in satellite communication[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition,2014,26(1):42-48.
[5] 孙云山,张立毅,张锦,等.改进恒模盲均衡在医学CT图像盲恢复中的应用[J].仪器仪表学报,2012(04):878-884.
ZHAO Yunshan,ZHANG Liyi,ZHANG Jin,et al. Application of improved constant module blind equalization algorithm in medical CT image blind restoration[J]. Chinese Journal of Scientific Instrument,2012(04):878-884.
[6] 杜伟.高速MAPSK卫星通信系统关键技术研究与实现[D].北京:北京理工大学, 2015.
DU Wei. Research and implementation on key technologies of high-speed MAPSK satellite communication system[D]. Beijing:Beijing Institute of Technology,2015.
[7] ABRAR S,ALI A,ZERGUINE A,et al. Tracking Performance of Two Constant Modulus Equalizers[J]. IEEE Communications Letters, 2013,17(5):830-833.
[8] COSKUN A, KALE I. All-Adaptive Blind Matched Filtering for the Equalization and Identification of Multipath Channels—A Practical Approach[J]. IEEE Transactions on Circuits & Systems I Regular Papers, 2013, 60(1):232-242.
[9] XIAO Y,RUAN R. CMA Blind Equalization with Variable Momentum Based on Nonlinear Transformation Function[J]. Applied Mechanics & Materials,2014(602-605):2658-2661.
[10] ABRAR S,NANDIA K. An Adaptive Constant Modulus Blind Equalization Algorithm and Its Stochastic Stability Analysis[J]. IEEE Signal Processing Letters,2010,17(1):55-58.
[11] 徐烽,邱乐德,王宇.APSK信号的混合盲均衡方法[J].重庆邮电大学学报:自然科学版,2013,25(5):605-610.
XU Feng,QIU Lede,WANG Yu. Hybrid blind equalizing method for APSK signals[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition,2013,25(5):605-610.
[12] OH K N, CHIN Y O. Modified constant modulus algorithm: blind equalization and carrier phase recovery algorithm [C]// IEEE International Conference on Communications. Seattle,America: IEEE Press, 1995:498-502.
[13] 宁小玲,刘忠,罗亚松,等. 适用于高阶QAM信号的水声信道修正盲均衡算法[J]. 重庆邮电大学学报:自然科学版,2011, 23(5):516-520.
NING Xiaoling,LIU Zhong,LUO Yasong,et al. Improved blind equalization algorithm suitable for high-order QAM signals used in underwater acoustic channels[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition,2011, 23(5):516-520.
[14] HAGER C,GRAELL I A A,ALVARADO A,et al. Design of APSK Constellations for Coherent Optical Channels with Nonlinear Phase Noise[J]. IEEE Transactions on Communications,2012, 61(8):3362-3373.
[15] YUAN J T,LIN T C. Equalization and carrier phase recovery of CMA and MMA in blind adaptive receivers[J]. IEEE Transactions on Signal Processing,2010,58(6):3206-3217.

