基于RGB通道下模糊核估计的图像去模糊
徐弦秋,刘宏清,黎 勇,周 翊
(重庆邮电大学 移动通信技术重庆市市级重点实验室,重庆 400065)
0 前 言
图像在获取的过程中,总是会受外界条件和周围环境的影响,导致图像质量受损。因拍摄过程中的相机抖动和对焦不准确而产生的图像模糊是最常见的一种图像受损。随着手持拍摄设备的流行,如何得到一种能够从捕捉到的图像中去除图像模糊的方法已经成为研究的关键。
根据受损图像信息重建清晰图像的方法已经有很多,现存的方法中大致可以分为2类:①利用已知的模糊核函数去除图像模糊的非盲去模糊;在模糊过程未知的情况下,估计出模糊核并重建清晰图像的盲去模糊[1-2]。很显然,自然图像在获取过程中所受到的模糊损坏,其模糊过程和原始清晰图像信息都是未知的,如何精确地估计出模糊核函数是需要关注的主要问题。Fergus等[3]以混合高斯模型匹配自然图像的重尾分布特征作为先验知识,应用到贝叶斯框架中进行模糊核估计;Shan等[4]提出了一种交替优化方法,同时对模糊核和潜在图像信息进行联合估计,但是算法的复杂度相对较高;在大部分现有的方法中,通常都是将自然彩色图像转化为灰度图像进行模糊核提取。事实上,数字照相机获取的彩色图像可以看做是3个色彩分量图的叠加,即红色、蓝色和绿色(red green and blue,RGB)分量,模糊核函数对每一个色彩分量图的影响是不同的。忽略不同分量图中模糊核的差异将会给接下来的图像恢复过程带来无法避免的失真影响。
近年来,信号的稀疏表示已经成为研究热点。文献[5]利用小波框架系统构造字典,对图像信号进行稀疏表示,建立图像复原模型,从而获得清晰的复原图像。但这种由固定变换域解析得到的字典,缺乏自适应性。传统的基于自适应字典的稀疏表示通常是以图像块(patch)为基本单位,这种模型把每一个图像块当做独立的对象处理进行稀疏编码。实际上,图像信号在非局部区域也具有相似性的特点。文献[6]提出一种图像非局部中心化稀疏表示模型,充分利用了图像非局部冗余特性,降低了稀疏编码过程中的噪声。但该方法没有充分结合图像局部自适应的特点建立稀疏表示表示模型。文献[7]提出一种三维块匹配算法(block matching 3D,BM3D),利用相似图像块匹配得到三维数组,用联合滤波的方法对三维数组进行处理,逆变换后,把处理后的结果返回到原图像中,从而得到去噪后的图像。该算法在去噪和图像复原上均取得了较好的效果,但联合滤波算法的复杂度有待降低。
针对图像模糊核只考虑在灰度域进行估计可能存在误差的情况,本文提出一种在RGB通道中分别估计模糊核函数的方法,然后针对不同分量图所得到的模糊核,充分利用自然图像自身特点,以结构组为基本单位代替单一的图像块建立组稀疏表示模型进行图像复原。首先,我们在多尺度条件下,通过预测图像显著边缘信息,并应用于高斯正则化模型,估计出不同通道中的模糊核函数;然后,利用得到的模糊核,在不同的色彩通道分量图中,以欧氏距离查找相似图像块构造结构组,利用结构组中相似的图像块应该具有相同字典的思想,获得图像信号的自适应字典,并建立图像复原模型进行去模糊处理。仿真结果表明,与只考虑在灰度域中获取模糊核函数的情况相比,使用不同通道下的模糊核进行图像恢复,获得了更好的效果,且利用组稀疏表示模型进行图像去模糊相比于传统的稀疏表示模型去模糊效果更加显著。
1 RGB通道下的模糊核估计
1.1 模糊图像模型
图像模糊过程可以被描述为清晰图像与点扩散函数(point-spread-function,PSF)的卷积加上噪声,即
g=h*f+n
(1)
(1)式中:*代表卷积操作;g,h和f分别是模糊图像、点扩散函数(也称为模糊核函数)和清晰图像;n是噪声。图像去模糊的目标就是从受损图像g中恢复出清晰图像f。
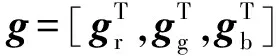
g=Hf+n
(2)
(3)
(3)式中,Hr,Hg和Hb分别代表每一个彩色通道内的模糊核函数。通过估计每一个通道内不同的模糊核函数来代替只考虑灰度域情况下的模糊核估计,以实现更好的图像复原效果。
1.2 RGB通道下的模糊核估计
边缘信息即使在其他结构被弱化的情况下也能够被很好地提取出来。因此,我们从观察到的模糊图像中尽可能准确地预测图像的边缘信息作为先验知识。一般来说,观测到的模糊图像通常伴随着噪声,噪声的存在将影响模糊核的准确估计,给复原的图像带来严重的振铃效应。为了减少噪声的影响,我们采用高斯滤波器进行平滑操作,然后利用冲击滤波器进行边缘增强,即

(4)
由于冲击滤波器在增强边缘信息的同时也增强了噪声,尤其对于不显著的边缘信息,噪声的影响将会更加严重。而且对于尺寸较大的模糊核函数来说,选择多余的边缘信息反而会影响对模糊核的精确估计。因此,我们只选择部分显著的图像边缘作为先验知识。通过把图像梯度转换到极坐标系内,在各个方向分别挑选梯度最大的部分。阈值t由图像和模糊核的大小决定,即
(5)
(5)式中,Pi和Pk分别代表图像和模糊核的总像素数。
类似于公式(1),清晰图像与模糊图像的边缘信息之间也遵循相同的关系,即

(6)


(7)
(8)

关于模糊核的先验知识可以用来优化模糊核函数的估计值。一般来说,模糊核函数值非负且和为1。本文中,我们将剔除一部分负的元素值,只保留模糊核中最重要的部分结构,并对模糊核进行归一化处理。
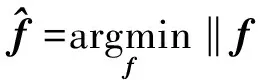

(9)
同样地,我们可以利用FFT变换得到(9)式的封闭解,则清晰图像的粗略估计值可以写作
(10)
为了保证模糊核的精确估计,我们在多尺度条件下分RGB通道进行。分别对RGB三幅分量图建立图像金字塔,从低分辨率分量图开始处理,用上述方法进行模糊核估计和粗略估计得到的清晰图像,然后利用重建图像作为新一层的高分辨率图像的初始图像,直到恢复出精确的模糊核。图1给出了在RGB通道中分别估计得到的模糊核,图1中的右下角的小图描绘的为模糊核的形状信息。由图1可以看出,虽然模糊核轮廓大致相同,但是无论是形状还是值的分布上,都是存在差异的。忽略这种差异将导致接下来的图像复原存在误差。

图1 RGB通道中分别估计得到的模糊核函数Fig.1 Estimated blur kernels from RGB channels
2 RGB通道下基于组稀疏的图像去模糊
在获得RGB通道的模糊核后,图像去模糊问题可以转化为解反卷积问题。如何充分对图像信号进行稀疏表示,建立完美的图像复原模型,成为求解的关键所在。
2.1 构造组稀疏模型
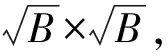
用RGi(·)表示从图像x中获得结构组xGi,结构组的匹配过程可以表示为
xGi=RGi(x)
(11)
对于每一个结构组xGi,我们希望通过自适应学习得到一个字典DGi,可以利用字典中的几个原子精确表示出结构组,即
(12)
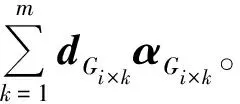
(13)
类似于文献[8]中字典学习的方法,我们用真实图像的估计值Z代替真实图像构造结构组,估计值可以通过优化求解获得。每一个结构ZGi组的字典可以通过奇异值分解(singular value decomposition,SVD)得到
(14)
(14)式中:SGi=diag(δGi)为对角阵;uGi×k和vGi×k分别表示UGi和VGi的列向量。定义字典中的原子dGi×k∈RB×c为
(15)
结构组的字典DGi∈R(B×c)×m最终可以表示为
DGi=[dGi×1,dGi×2,…,dGi×m]
(16)
2.2 RGB通道下的图像去模糊
建立字典后,利用我们估计得到的RGB通道中的模糊核,可以得到基于组稀疏下的图像复原优化模型,即
(17)
我们采用分裂伯格曼迭代算法[9](split bregman iteration,SBI)进行(17)式的优化求解。SBI算法通常用来解决优化问题,即
(18)
(18)式中:G∈RM×N;f:RN→R;g:RM→R均为凸函数。根据SBI算法,(18)式可以看作是2个子问题的求解。通过引入变量u,优化问题转化为
s.t.u=DG°αG
(19)
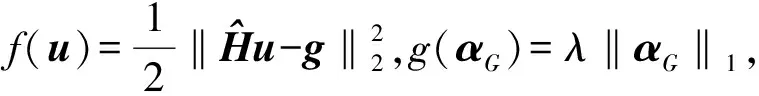
(20)
2.2.1u子问题求解
在给定αG时u子问题可以看做一个严格的二次凸优化问题,即
(21)
可以直接求得u的封闭解,即
(22)
2.2.2αG子问题求解
给定u,令z=u-b,则αG子问题可以转化为
(23)
z实际上可以看做是输入的真实图像,我们通过迭代z(t)=u(t)-b(t-1)可以得到z(t)。实验结果表明,在第t次迭代时,以下等式可以成立,即
(24)
代入到(23)式,有
已知xGi=DGiαGi,zGi=DGiδGi,根据字典的酉特性,可以得到
(25)
上述求解过程可以看做是求解每一个结构组的子问题,等价于
(26)
可以获得(23)式的封闭解,即
(27)
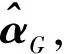
3 仿真结果与分析
本文仿真实验中,进行模糊核估计时,模糊核尺寸根据所添加模糊类型确定,规则化参数分别为γ=10,γ1=2e-3。组稀疏模型中,每一个结构组大小为64×60,分割的图像块之间重叠4个像素,所以有I=240N,搜索窗口大小为40×40。实验共对4幅彩色图片进行仿真如图2所示。仿真图片使用高斯模糊和运动模糊2种模糊核类型,λ,μ的取值由模糊核类型确定。

图2 仿真自然彩色图片Fig.2 True color image for simulations
本文采用主观视觉比较和峰值信噪比(peak signal to noise ratio,PSNR)作为评价图像恢复质量的指标。峰值信噪比定义为
(28)
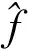
通过比较使用RGB通道中分别获得的模糊核与只考虑灰度域获得的模糊核进行图像去模糊的效果,并且将本文的方法与利用非局部冗余特性的NCSR(nonlocally centralized sparse representation)方法[6]以及三维块匹配的BM3D方法[7]作对比。
由于主观视觉上不如客观数据能更直观的反映复原效果。因此,本文把仿真图片P3和P4的恢复效果图做为举例说明,所有仿真图片复原处理的PSNR具体数据在表1中详细列出。
图2和图3分别给出了图片P3在σ=3的高斯模糊下的恢复效果,以及图片P4在线性运动模糊下的恢复效果,具体的PSNR值在表1中详细给出。可以看出,与BM3D和NCSR相比,本文方法获得的复原图像效果较好,且相对于只考虑利用灰度域获得模糊核的情况,利用RGB通道中得到的模糊核进行图像去模糊处理,获得的图像更加清晰。

图3 彩色图像P3去模糊的视觉效果比较Fig.3 Visual quality comparisons of image deblurring on color image P3
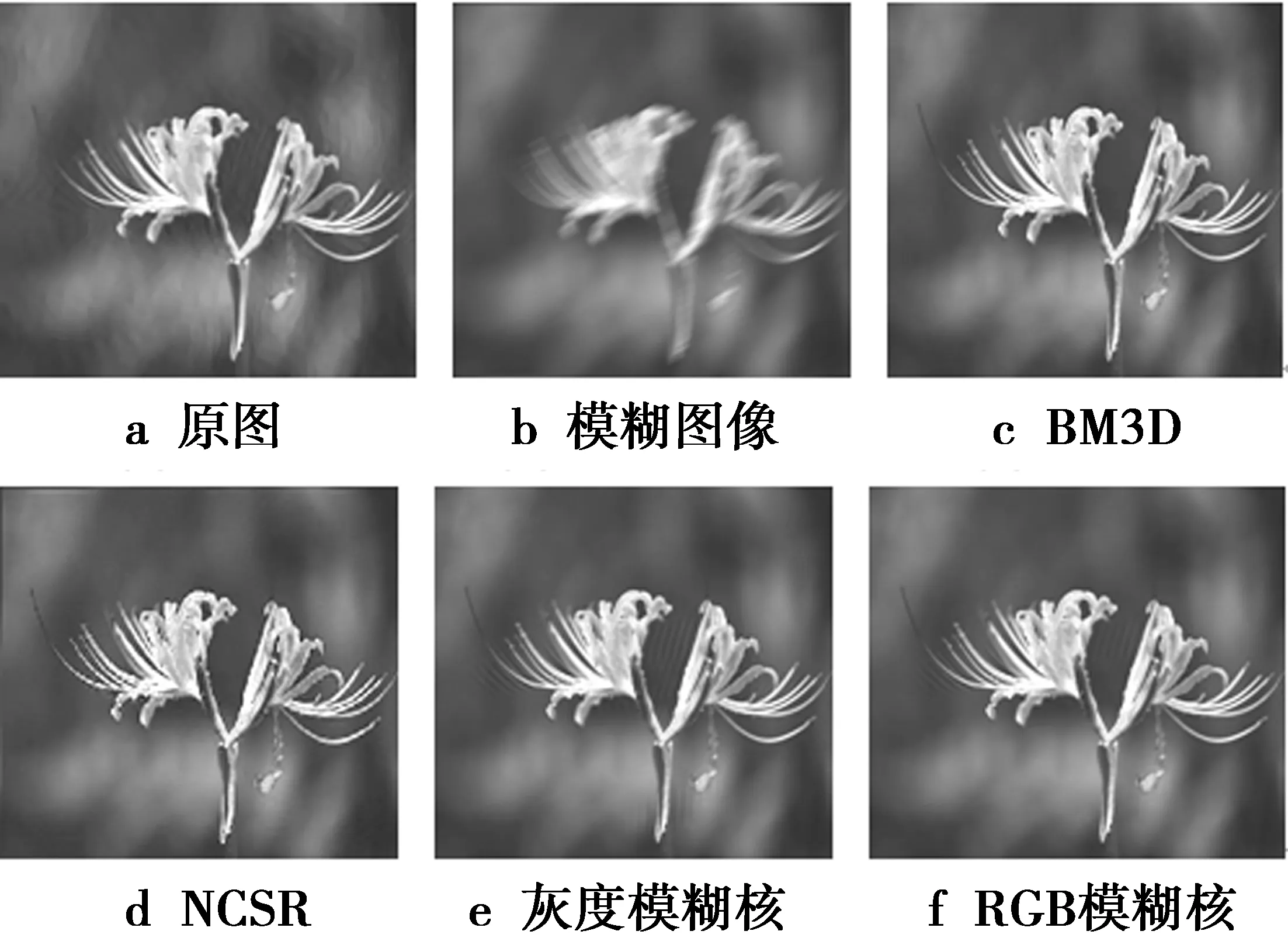
图4 彩色图像P4去模糊的视觉效果比较Fig.4 Visual quality comparisons of image deblurring on color image P4
表1给出了4幅仿真图片在2种不同模糊情况下,本文方法中利用灰度域和RGB通道下分别估计的模糊核所得到复原图像PSNR值,以及BM3D[6]和NCSR[7]2种方法得到的复原图像的PSNR值。效果显著的方法的数值在表1中用黑色字体标出。比较数据发现,在高斯模糊下图片P1和P3的复原结果中,与BM3D相比,PSNR值分别提高了0.63 dB和1.44 dB;在线性运动模糊下图片P2和P4的复原结果中,利用RGB通道中获得的模糊核进行图像复原的PSNR相比于只考虑灰度域模糊核的图像复原的PSNR值分别提高了0.14 dB和0.78 dB。

表1 2种典型模糊类型下图像复原的PSNR值比较
4 结论
本文在RGB通道中分别进行模糊核函数的估计,针对不同通道所得到的模糊核,充分利用图像信息的局部平滑和非局部自相似的特点,以结构组为基本单位代替单一的图像块建立组稀疏表示模型进行图像复原。仿真结果表明,本文方法在处理图像细节及PSNR上优于现有方法,且与目前只考虑利用灰度域估计模糊核进行图像复原的方法相比,获得了更加清晰的图像效果。
参考文献:
[1] YANG Haoliang, HUANG Pohao, LAI Shanghong. A novel gradient attenuation Richardson-Lucy algorithm for image motion deblurring[J]. Signal Processing, 2014(103):399-414.
[2] 李鑫楠.图像盲复原算法研究[D].吉林:吉林大学,2015.
LI Xinnan. The study on blind image restoration algorithms[D]. Jilin: Jilin University , 2015.
[3] FERGUS R, SINGH B, Hertzmann A, et al. Removing camera shake from a single photograph[J]. ACM Transactions on Graphics, 2006, 25(25):787-794.
[4] SHAN Q, JIA J, AGARWALA A. High-quality motion deblurring from a single image[J]. ACM Transactions on Graphics, 2008, 27(3):15-19.
[5] JI H, WANG K. Robust image deblurring with an inaccurate blur kernel[J]. IEEE Transactions on Image Processing, 2012, 21(4):1624-34.
[6] MAIRAL J,BACH F,PONCE J,et al.Non-local sparse models for image restoration[J].2009,30(2):2272-2279.
[7] DANIELYAN A,KATKOVNIK V,EGIAZARIANK.BM3D frames and variational image deblurring[J].IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2011, 21(4):1715-1728.
[8] GOLDSTEIN T, OSHER S. The Split Bregman Method for L1-Regularized Problems[J]. Siam Journal on Imaging Sciences, 2009, 2(2):323-343.
[9] ZHANG L, DONG W, ZHANG D, et al. Two-stage image denoising by principal component analysis with local pixel grouping[J].Pattern Recognition,2010,43(4):1531-1549.

