基于RBF神经网络的无刷直流电动机故障诊断
王 炜,钟书辉
(中国空空导弹研究院,洛阳 471009)
基于RBF神经网络的无刷直流电动机故障诊断
王 炜,钟书辉
(中国空空导弹研究院,洛阳 471009)
摘 要:为尽可能检测空空导弹舵机多种故障,提出采用导弹舵机三相工作电流作为舵机故障诊断的信号源,针对舵机无刷直流电动机驱动器的开路、短路等故障,在MATLAB中构建无刷直流电动机及驱动器的模型,并进行故障仿真。选取Haar小波基函数对故障信号进行提取、分析和处理,利用提取的故障特征值对起到故障识别作用的RBF神经网络进行训练。仿真结果证明,训练得到的RBF神经网络能够有效识别出舵机中无刷直流电动机驱动器的故障,表明该方法的正确性。
关键词:故障诊断;无刷直流电动机;小波分析;RBF神经网络;MATLAB
0 引 言
舵机作为空空导弹的执行机构,其性能好坏对于导弹飞行中的动态品质起着决定性的作用[1],但空空导弹的战术使用特点是长期存储、短时使用。因此,对于舵机的故障检测和诊断便成为提高舵机可靠性、判断舵机工作状态、评估舵机健康性的重要手段。目前常见的舵机故障检测和诊断方法主要分为基于模型和基于信号两大类。
基于模型的舵机故障诊断计算需要建立舵机的精确模型。如杨秉岩[2]等采用构建舵机传动机构的传递函数,对舵机故障进行分类和诊断,但仅能表明舵机内部元器件有可能发生故障,无法确定故障类型和原因。为此,又有学者提出采用自适应观测器[3-4]的方法,利用序列概率比进行故障决策。但该方法因建立精确的舵机模型较为困难,且计算过程较为复杂,难以得到广泛应用。
近年来,随着数字信号处理技术的快速发展,将电机的母线电流作为故障诊断的信号源,研究其特征与故障的对应关系,已成为基于信号处理的故障诊断方法的新研究趋势[5]。该方法不需要增加额外的传感器来获取故障信号,不仅可检测到电机故障,还可检测到电机驱动器、齿轮组等故障,因此得到广泛的应用[6-9]。由于小波分析对时变、短时冲击、突发信号等具有良好的分析能力,在电机故障诊断中应用较多[10]。然而,小波分析只能定位故障发生时间,不能定位故障发生环节,故需引入神经网络等作为故障识别与诊断环节。由小波分析等提取故障发生时特定信号的频谱,将其转化为故障特征值,并以其为输入值,对充当故障识别环节的神经网络进行训练,最终验证训练结果。在选定神经网络时,需要考虑到通常此类故障的样本量较少,需选取合适的神经网络,以确保神经网络的训练和验证不会受到影响。
故本文选取电动舵机中无刷直流电动机的三相母线电流为故障信号源,以电机驱动器开关管短路、断路等故障为研究对象,通过信号处理方法提取其故障特征值,对故障进行识别、诊断和定位。
1 电动舵机组成及工作原理
电动舵机是空空导弹上重要的伺服机构系统。电动舵机一般由舵机控制器、电机驱动器、直流电动机、齿轮传动副、滚珠丝杠和反馈装置等组成,其中直流电动机和齿轮传动副、滚珠丝杠等称之为舵机的传动机构。图1为电动舵机系统主要组成框图。

图1 电动舵机组成示意图
电动舵机的工作原理是:电动舵机接收飞控/制导计算机给定的舵面偏角信号,经由电路上的控制电路处理后,生成驱动器逻辑控制信号,由驱动器驱动电机开始转动,经过齿轮传动副和滚珠丝杠组成的减速装置将动力输出到舵轴,驱动舵面转动,同时与舵轴相连的位置传感器(反馈装置)送回检测信号,判定舵面是否已经到达位置。
由电动舵机组成可见,无刷直流电机是其最重要的组成部分。无刷直流电机的故障也就成为电动舵机故障检测的重要组成部分。
2 无刷直流电机故障诊断系统
无刷直流电机发生故障时,故障信号呈现瞬态、冲击、非平稳的特点。小波分析采用多分辨率分析,可同时反应故障信号在时域、频域上的特征,能够有效提取故障特征值,在故障诊断领域得到了广泛的使用。然而小波分析仅能提取故障特征值,当故障特征值数量较多、故障类型较多时,则需要引入专门的故障分类器,对故障进行准确定位。人工神经网络以其良好的学习能力,可发现系统内难以解析的规律,故作为故障分类器用于故障诊断。小波分析与神经网络的松散结合也是常见的故障诊断模式。
2.1 小波分析提取故障特征
2.1.1 小波分析工作原理
小波函数系是小波分析的核心基础,小波分析的主要操作是利用小波函数系对所需分析的信号或函数进行表示、逼近,实现信号或函数的重构。而小波变换则是将时间函数同各自基函数进行卷积计算,属于内积运算,同时把信号分解成不同尺度的分量。基小波或者母小波定义如下:设φ(t)为一平方可积函数,若其傅氏变换Ψ(ω)满足可容许性条件,即有:
(1)
满足上述条件的φ(t)就可称做小波的一个母函数(基本小波)。φ(t)在时域和频域上进行伸缩和平移,得到的函数称之为连续小波基函数:
(2)
式中:a的值变化将会对信号进行不同的带宽滤波,在频域上体现为小波分析对信号的频率局部化特性分析结果。b的值变化则可让小波函数沿时间轴进行滑动,在时域上表现为小波分析对信号采样步长的变化。
在得到连续小波基函数后,则可对于任意函数f(t)∈L2(R)进行小波分析,称之为连续小波变换,具体:
(3)
式(3)表示了小波分析的时频特性,也表明了小波分析的最大优势即局部分析能力。当时域观测宽度变大时,对应在频域上的频率区间就会减少,并且频率中心会向低频方向移动。反之,时域观测宽度变小时,频域上的频率区间就会增加,频率中心向高频移动。
2.1.2 故障特征值提取
小波分析对信号层层分解过程中,在每一层分解中都将信号分解为低频和高频两部分,并只对低频部分进行分解,高频部分则被保留,由上一层进行分解。图2所示为小波分解示意图,对于信号B进行3层小波分解。其中a1,d1,a2,d2,a3,d3为小波分解在不同层次上的系数。且有:
B=a1+d1=a2+d2+d1=a3+d3+d2+d1
(4)
该系数能够反映信号B在不同频带上的特性,因此小波分解系数可直接用作故障特征值。

图2 小波分解示意图
2.2 RBF神经网络进行故障诊断
径向基函数神经网络(以下简称RBFNN) 是3层前向神经网络[12]。第一层是包含若干个输入信号源节点[X1,X2,…,Xn]的输入层。第二层是根据所需要解决问题而包含不同节点[R1,R2,…,Rh]的隐藏层。对于RBF神经网络而言,RBF的作用是充当隐藏层中的神经元变换函数。第三层是对输入做出响应的输出层,根据问题需要包含不同的节点数量[Y1,Y2,…,Ym],每个节点都与隐藏层中的所有节点发生关系,得到一个权值Wij(i∈[1,h],j∈[1,m])。图3所示为RBFNN的组成示意图。
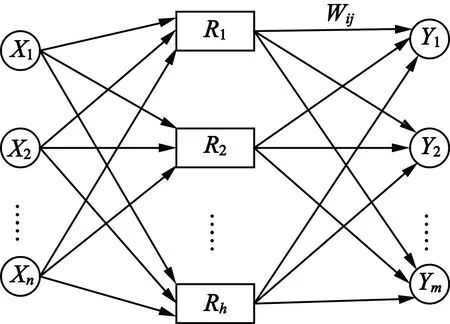
图3 RBFNN组成示意图
由图3可见,RBFNN基本思想是将在低维空间属于线性不可分问题,通过RBF构成的隐含层可以把低维的输入转换到高维空间,在高维空间内寻求线性可分的可能性,进而实现问题的求解。较其他智能故障判断标识手段,在结构复杂性、训练速度和学习收敛方面具有明显优势,故在故障诊断领域广泛使用。
与其它智能故障判断方法相似,RBF神经网络首先也需要训练,也就是由若干组故障特征值组成训练组,作为RBF神经网络的输入值,对RBF神经网络进行训练,故障分类则是RBF神经网络的输出值。训练后得到的RBF神经网络还需要通过与训练组不同的故障特征值进行验证,检验RBF神经网络的故障识别能力。
3 仿真验证
3.1 故障选取
对于无刷直流电机而言,驱动器作为无刷直流电机电压转换部分,如果发生故障,将会对电机的运转产生危害,同时影响电机的带载能力。研究表明:变频调速系统中功率变换器是驱动系统中的薄弱环节,其故障比例占整个系统故障的82.5%[13]。为此,选取驱动器故障作为无刷直流电机的典型故障进行分析。图4为BLDCM驱动示意图。
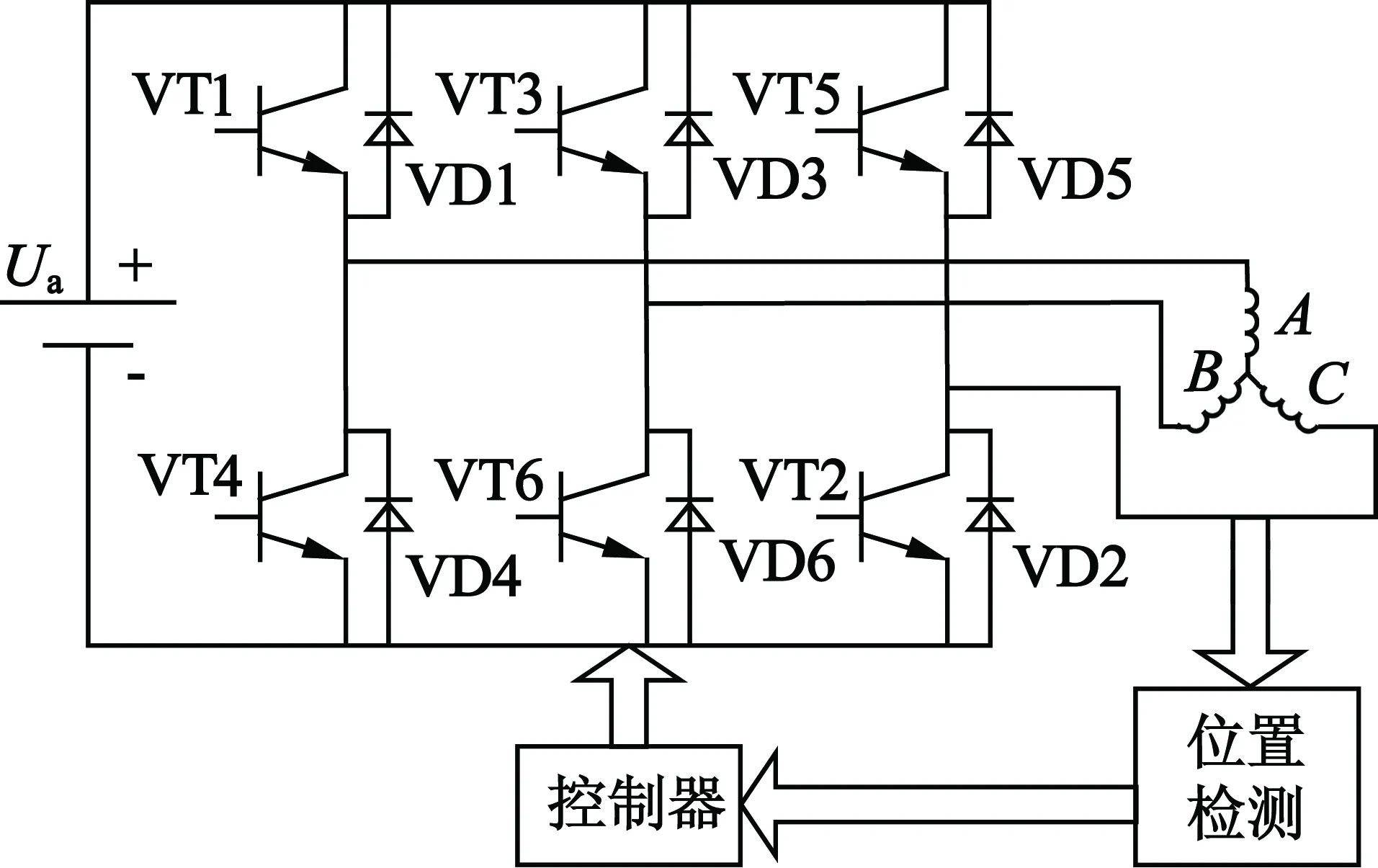
图4 BLDCM驱动示意图
为简化分析,规定在任意时刻,晶闸管VT1~VT6中仅有1个晶闸管发生故障,故障类型为短路或开路。如此便有12种故障模式。再加上驱动器正常工作状态,共有13种故障模式。
3.2 故障特征值提取
针对无刷直流电机驱动器开关管开路、短路故障,以无刷直流电机三相工作电流为故障信号源,利用小波变换对其进行信号分析,提取故障特征值。由于小波分析时选取的小波基函数和分解层数不同,得到的结果也各不相同。在经过大量小波基函数和分解层数的选取、试验之后,最终发现,当选取Haar小波基函数,并进行5层分解得到的故障特征值最为明显。如图4中的VT1在0.3~0.32 s发生短路故障,利用小波分析对A相电流进行分析,结果如图5所示。可以看出,在0.3~0.32 s之间,A相电流经过Haar小波5层分析重构后,在d1,d2和d5三个层次上表现的最为明显,分别如图5所示。

(a) d1重构
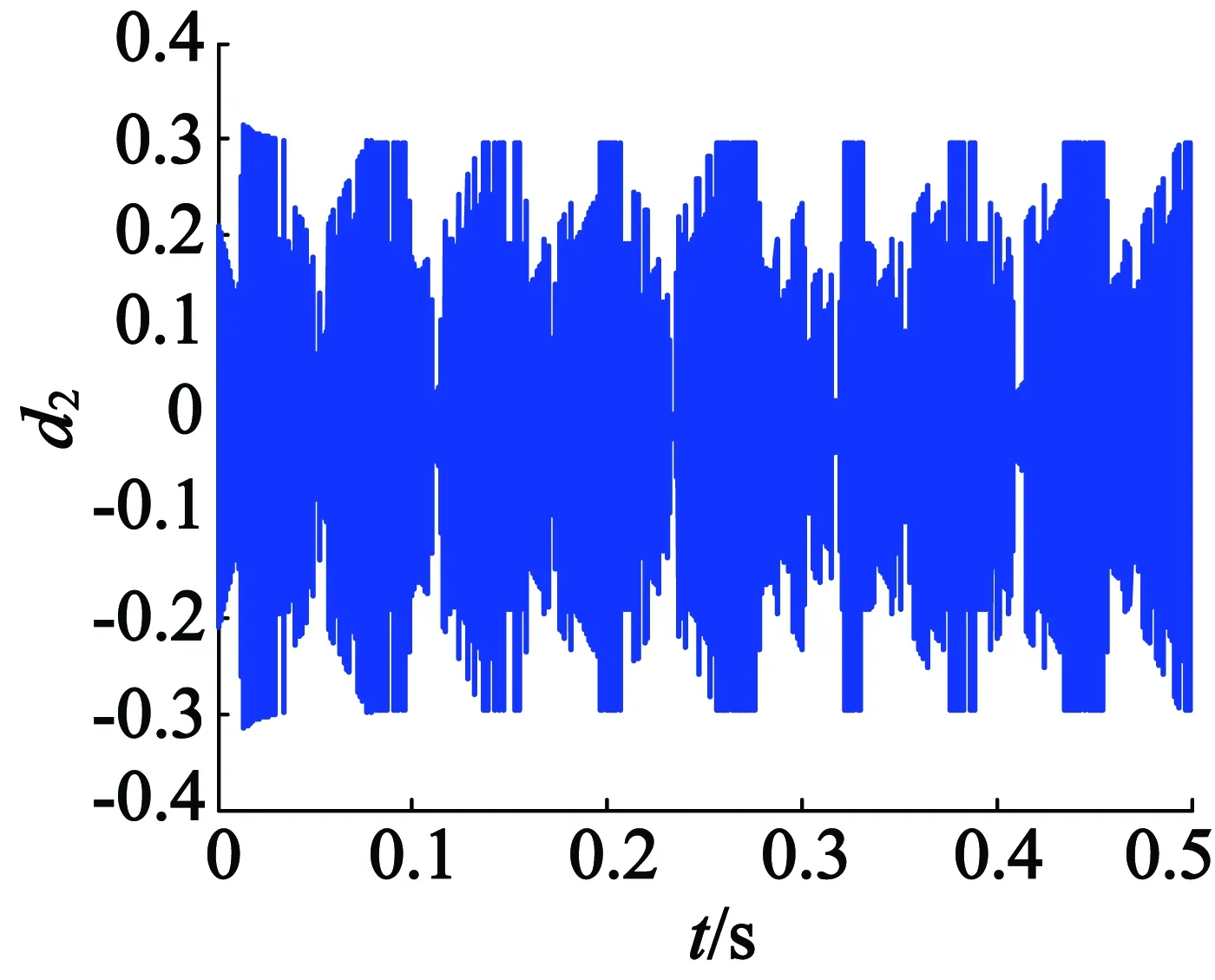
(b) d2重构
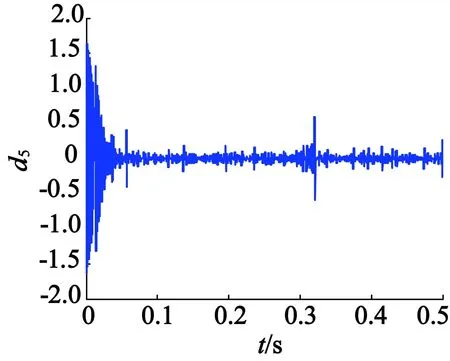
(c) d5重构
同样对B,C两相电流进行Haar小波5层分析,结果与图5相似。如选取每相电流经过Haar小波5层分析的系数(a5,d1,d2,d3,d4,d5)为故障特征值,则对于单个开关管故障,可以得到的典型故障特征值共有18个。
3.3 故障识别
故障特征信号提取完毕后,仅能表现出在某时间段内发生故障,但对于故障类型和故障部位不能确定。需要利用故障特征值对RBF神经网络进行训练。
为了能够使得RBF神经网络区分故障类型,要对驱动器中的6个开关管和故障类型分别进行编码,一是利于快速确定开关管的编号,二是确定开关管故障类型。因此,得到编码方式如表1所示。

表1 故障类型及编码
S1S2表示是否发生故障和故障类型,没有故障即为正常状态,编码为00,如果发生开路故障,则编码为01;短路故障为10。S3S4S5表明VT1~VT6哪个开关管发生故障,正常状态对应的故障编码为000,VT1~VT6的对应编码分别是001,010,011,100,101,110。
如此RBF的输出就为一组5位编码。而输入有13种状态,每种状态取3种故障征兆,每个故障征兆有6个数据。
对本文建立的RBF神经网络采用20组数据进行训练,6组数据进行测试。如此RBF的神经网络输入数据为(13*3*6)*20组数据,输出为(13*5)*20组数据。
对于上述故障提取到的故障特征数值,首先采用正常状态和VT1开路两种状态下的故障特征数值进行训练,对照表1可知,期望输出值为[0 0 0 0 0 0 1 0 0 1],对于2组状态分别选取了20组数据进行训练,利用另外6组数据进行验证,6次验证结果均为[0 0 0 0 0 0 1 0 0 1],表明RBF神经网络可有效地识别出正常和VT1开路两种状态。
对于13种故障状态的校验结果如表2所示。
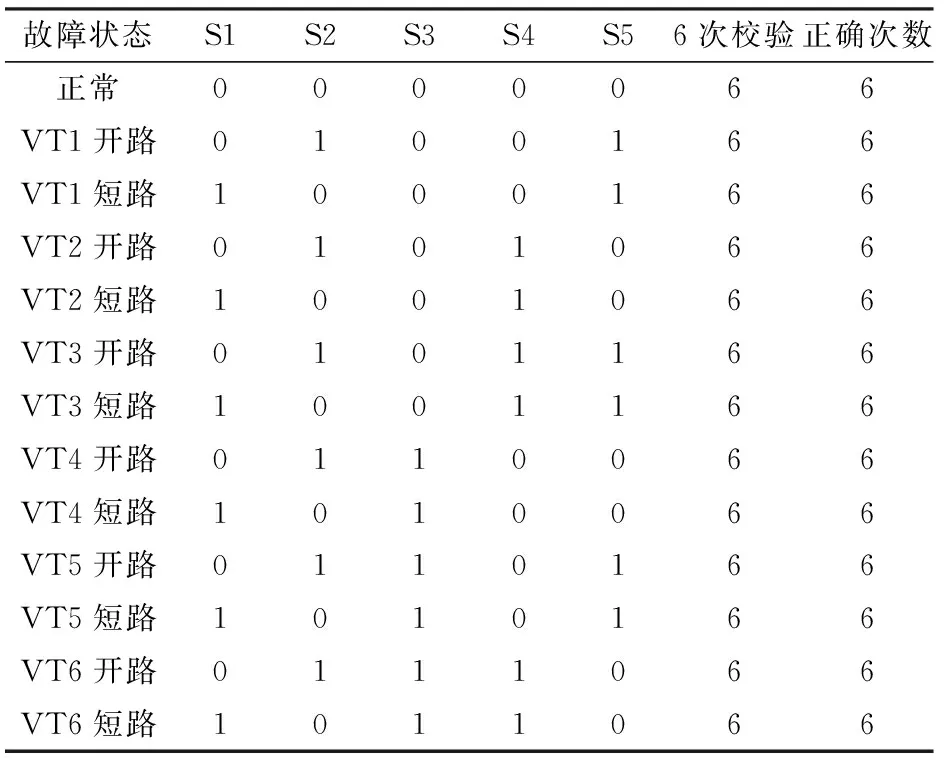
表2 无刷直流电动机驱动器故障诊断结果
由此可见,本文所设计的RBF神经网络对于无刷直流电动机驱动器的13种故障的识别率可以达到100%,表明该方法的正确和有效性。
4 结 语
本文以空空导弹电动舵机中所用的无刷直流电动机为研究对象,通过小波分析提取无刷直流电动机驱动器故障时的故障特征值,将其作为RBF神经网络的输入,对其进行训练和校验。结果表明,本文得到的RBF神经网络能够有效地识别13种故障,识别率达到了100%,验证了故障诊断方法的可行性,并取得了较好的诊断效果。
[1] 樊会涛. 空空导弹方案设计原理[M].北京:航空工业出版社,2013,1-10.
[2] 杨秉岩,程绍成,朱伟,等. 基于传递函数识别的导弹电动舵机故障诊断[J].海军航空工程学院学报,2012,27(5):494-498.
[3] 史贤俊,张文广,张艳. PSO-RBF 神经网络在舵机系统故障诊断中的应用[J].海军航空工程学院学报,2011,26(2):131-135.
[4] 廖瑛,吴彬,曹登刚,等. 基于自适应观测器的导弹电动舵机故障诊断研究[J].系统仿真学报,2011,23(3):618-621.
[5] 张琛.直流无刷电动机原理及应用[M].北京:机械工业出版社,2004.
[6] 刘志东,石山,陈硕勋,等. 基于1-DISVM 的无刷直流电机故障识别方法[J].微电机,2013,46(3):64-67.
[7] 吕永健,李子龙,张洪林. 基于改进遗传小波网络的电机故障诊断研究[J]. 微特电机,2012,40(4):19-22.
[8] 贺昌权 包广清. 基于小波变换的无刷直流电机逆变器故障检测仿真研究[J].微电机,2010,43(1):74-77.
[9] 王瑞梓. 基于小波与感应电机电流的齿轮传动系统故障诊断[M].沈阳:东北大学,2008.
[10] 杨欣荣,蒋林,王婧林,等. 基于小波变换的无刷直流电机逆变器故障诊断[J].电测与仪表,2017,54(5):113-118.
[11] 侯晓松. 基于DSP的弹上舵机控制系统的设计[D].西安:西安电子科技大学硕士论文,2008.
[12] 贺昌权,包广清. 基于小波变换的无刷直流电机逆变器故障检测仿真研究[J]. 信息化纵横,2009(11):73-76.
[13] 史峰,王小川,郁磊,等.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学,2010.
TheFault-DetectionSystemwithBrushlessDCMotorBasedontheWavelet
WANGWei,ZHONGShu-hui
(China Airborne Missile Academy, Luoyang 471009,China)
Abstract:In order to detect more servo system's faults of air-to-air missile, a method was proposed that the three-phase current of motor in the servo system of missile was chosen to be the fault-detection signal. A fault model of the brushless DC motor and driver were built under MATLAB. The fault signals were analyzed by the wavelet and transferred to the RBF network which was used to train the analyzed signals. The test results of RBF showed the method could effectively distinguish the motor driver's fault.
Key words:fault-detection; brushless DC motor; wavelet; RBF network; MATLAB
中图分类号:TM33
A
1004-7018(2018)05-0044-04
2018-01-30
航空基金项目(2016ZD12028)
作者简介:王炜(1978—),男,博士,研究方向为伺服系统控制。

