一种平稳子空间分析的快速不动点算法
林原灵,陈 前
(南京航空航天大学航空宇航学院机械结构力学及控制国家重点实验室,江苏 南京 210016)
0 引 言
平稳性假设是信号处理、机器学习、数据挖掘等学科内众多理论和模型的基础性假设[1]。但在现实应用中,大量的观测信号是非平稳的。为了有效地分析非平稳信号,一种思路是假设观测到的非平稳信号中隐含着平稳成分,通过消除非平稳性的影响将平稳成分提取出来,再分析提取出的平稳成分。沿着上述思路,文献[2]提出了平稳子空间分析(Stationary Subspace Analysis, SSA)技术,用于从观测到的多维非平稳信号中分离出平稳源信号。与独立成分分析(Independent Component Analysis, ICA)等经典的盲源分离算法[3-9]不同,平稳子空间分析技术只考虑源信号的平稳性,对源信号的独立性没有要求。目前,平稳子空间分析技术已经在气象信号处理[10]、生物医学工程[11-12]、旋转机械信号处理[13-14]等领域得到了成功的应用。
在文献[2]中,平稳子空间分析被转化成一个正交约束条件下的最优化问题,文献[2]建议使用Stiefel流形上的梯度下降算法[15]求解平稳投影矩阵。目前,该算法得到了广泛的应用[11,13-14]。但是,Stiefel流形上的梯度下降算法收敛较慢,需要选择合适的梯度下降步长,因而计算量大,耗时多。不动点算法形式简单,不需要调整梯度下降步长,如果迭代公式构造恰当,往往收敛快,耗时少[3-9]。文献[10]提出了一种适用于平稳子空间分析的不动点算法,但是,其仿真实验结果表明,在某些实验中,由其所提出算法求出的平稳投影矩阵与实际值之间存在较大偏差,不能准确地分离出平稳源信号。
在能够有效地分离出平稳源信号的前提下,为了加快算法的收敛速度,提高算法的运行效率,本文根据有关Stiefel流形上优化问题的一阶最优性条件,构造不同于文献[10]的迭代公式,提出一种新的适用于平稳子空间分析的不动点算法,应用该算法从仿真信号中分离出平稳源信号,验证了其有效性,并与Stiefel流形上的梯度下降算法以及文献[10]提出的不动点算法进行了性能对比分析。
1 平稳子空间分析原理
平稳子空间分析模型中,观测信号x(t)∈Rd可以分解成平稳源信号ss(t)∈Rm和非平稳源信号sn(t)∈Rd-m的线性组合形式:
(1)

文献[2]将观测信号的样本划分为N个不同的时间段,使用Kullback Leibler散度(Kullback Leibler Divergence, KLD)衡量平稳源信号的样本均值和样本协方差在各个时间段之间的差异,根据平稳信号的统计参数不随时间变化的性质,最小化平稳源信号的样本均值和样本协方差在各个时间段之间的KLD之和,建立关于平稳投影矩阵Bs的目标函数,得到如下的优化问题:
(2)
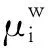
2 平稳子空间分析的不动点算法
Stiefel流形上的梯度下降方法收敛较慢,需要选取合适的梯度下降步长,因而计算量大,耗时多。因此,使用不动点算法[3-5]求解最优化问题成为另一种选择。不动点算法形式简单,不需要调整梯度下降步长,若结合具体的优化问题的特性,合理地构造迭代公式,则可以得到收敛更快,耗时更少的优化算法[3-9]。
2.1 基于一阶梯度的不动点算法

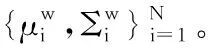
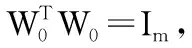
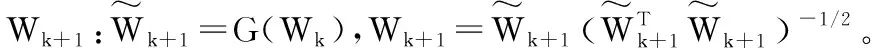

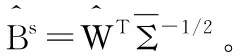
需要说明的是:1)对于给定的矩阵W∈Rd×m,式(2)中的目标函数相对于W的梯度矩阵G(W)的表达式为:
(3)
2)对矩阵W∈Rd×m的正交化处理,可以采用文献[3]建议的方法:
W←W(WTW)-1/2
(4)
从而使得WTW=Im;3)收敛条件中,一般取ε=10-5,εF=10-6。
2.2 基于Stiefel流形一阶最优性条件的不动点算法
文献[10]的仿真实验结果表明,在某些实验中,由文献[10]提出的不动点算法求出的平稳投影矩阵与实际值之间存在较大的偏差,无法有效地分离出平稳源信号。这是因为Stiefel流形上的目标函数在极值点处的解矩阵与该点处的梯度矩阵之间并不是如文献[10]所认为的简单地成正比关系,而是应当满足一阶最优性条件[16]。因此,文献[10]构造的迭代公式是不合理的。鉴于此,本文根据关于Stiefel流形上优化问题的一阶最优性条件,构造一种新的迭代公式,基于此迭代公式,提出一种新的平稳子空间分析的不动点算法。
定理1一阶最优性条件。对于Stiefel流形上的优化问题:
(5)
其中,f(W):Rd×m→R是可导函数。假设W是式(5)中最优化问题的一个局部极小值点,则W满足一阶最优性条件:
(6)

关于定理1的详细证明,可以参阅文献[16],兹不赘述。现将平稳子空间分析目标函数的梯度矩阵表达式(3)代入式(6),推导出关于W的方程:
(7)
(8)
根据式(8)和W的正交约束条件,本文构造了一个新的迭代公式:
(9)
基于式(9)的迭代公式,本文提出一种新的适用于平稳子空间分析的不动点算法,其具体流程如下:
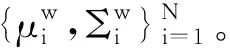
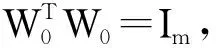
步骤3根据式(9)的迭代公式更新解Wk+1。

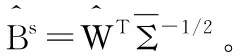
需要说明的是,式(2)中平稳子空间分析的目标函数是非凸的,无论是使用Stiefel流形上的梯度下降还是不动点算法,为避免得到局部最优解,应该使用不同的随机初始值多次求解,取使目标函数值最小的解。
3 算法仿真与性能分析
本章通过仿真实验比较不同的平稳子空间分析算法的性能。仿真实验环境为Intel Pentium 4 CPU 3.0 GHz,2 GB内存,100 GB硬盘,Windows XP系统,实验工具为Matlab R2014a。仿真实验中,选用一组三维的平稳源信号{ss(t)}和一组二维的非平稳源信号{sn(t)},源信号按照以下的自回归过程生成:
(10)
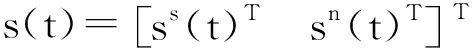
(11)
其中,As∈R5×3和An∈R5×2分别是平稳源信号{ss(t)}和非平稳源信号{sn(t)}的载荷矩阵。
3.1 分离效果比较
比较不同的平稳子空间分析算法从仿真信号{y(t)}中分离出平稳源信号{ss(t)}的能力,包括Stiefel流形上的梯度下降算法(简记为SSSA)、文献[10]提出的不动点算法(简记为fSSA)以及本文提出的不动点算法(简记为FSSA),其中SSSA采用文献[18]新近提出的Stiefel流形上的最优化框架,并基于Armijo准则[19]搜索选择梯度下降步长。

(12)

在仿真实验中,观测信号按照式(10)、式(11)的随机过程生成,样本长度为3000,其中自回归系数ai从区间(-0.5,0.5)上的均匀分布中随机采样,bj从区间(-1,1)上的均匀分布中随机采样,混合矩阵A的每个元素从均值为0、方差为1的正态分布中随机采样。仿真实验中时间段个数N分别取50至300间的不同值。3种算法在每一种时间段个数条件下不重复地仿真实验1000次,每次实验中,观测信号样本保持不变,每种算法使用5个不同的随机初值,选择目标函数最小值对应的解作为该算法的最优解BsT,再将该解与当次实验中的载荷矩阵An代入式(12)评估分离效果。

图1 仿真实验中平稳子空间分析算法得到的平稳投影张成子空间与实际子空间之间最大主角的误差棒图(纵坐标轴使用对数坐标)
图1给出了3种算法在仿真实验中,当时间段个数N取不同的值时,计算出的平稳投影矩阵张成的子空间与实际子空间之间最大主角的误差棒图。从图1所示的结果来看,在时间段个数取不同的值时,本文提出的不动点算法FSSA计算出的最大主角的平均值都接近于0°,标准差也很小,说明该算法分离出的平稳源信号与实际值之间的差异很小,并且该结果与Stiefel流形上的梯度下降算法SSSA得到的结果相一致;相反,由文献[10]提出的不动点算法fSSA计算出的最大主角的平均值在20°左右,并且标准差较大,未能有效地分离出平稳源信号,说明本文提出的迭代公式可以有效地收敛到最优解,而文献[10]提出的迭代公式确实无法有效地收敛到最优解。实验结果表明,本文提出的适用于平稳子空间分析的不动点算法能够有效地从观测信号中分离出平稳源信号,分离精度与基于Stiefel流形上的梯度下降算法相当,优于文献[10]提出的不动点算法。文献[10]提出的不动点算法分离效果欠佳,不宜在实践中使用。
3.2 计算效率比较
比较本文提出的不动点算法FSSA和Stiefel流形上的梯度下降算法SSSA的计算效率,而文献[10]提出的不动点算法由于分离性能欠佳不予考虑。在此仿真实验中,观测信号的生成方式与前一个实验保持一致。比较2种算法在时间段个数N分别取50至300间不同值时的效率,在每一种时间段个数条件下不重复地仿真实验10000次。在每次实验中,2种算法使用相同的观测样本和初始值。
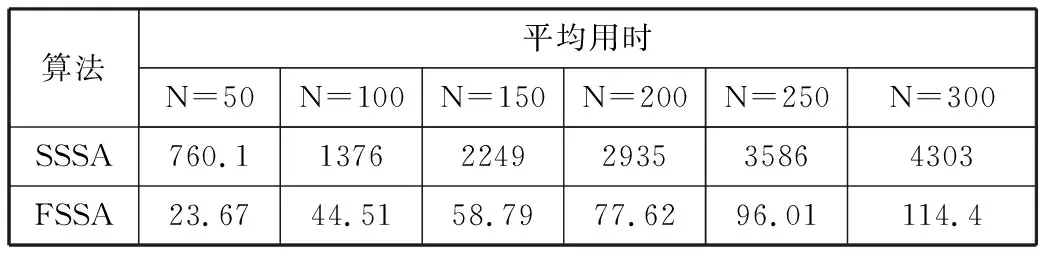
表1 仿真实验中平稳子空间分析算法的平均耗时 单位:ms
表1给出了这2种算法在时间段个数N取不同值时的平均耗时。从表1所示的结果来看,在时间段个数取不同的值时,本文提出的不动点算法FSSA的平均耗时都远小于Stiefel流形上的梯度下降算法SSSA。这主要是因为Stiefel流形上的梯度下降算法在迭代时需要搜索选择合适的梯度下降步长,因此计算量大,耗时多;相反,不动点算法不需要选取梯度下降步长。
进一步地,比较由公式(12)定义的评价指标在上述10000次仿真中的平均值。图2给出了时间段个数取不同的值时,2种算法在前20轮迭代中的实验结果。从图2所示的结果来看,在时间段个数取不同的值时,由本文提出的不动点算法求出的解随着迭代次数的增加均能够不断地收敛到最优解,相比于Stiefel流形上的梯度下降算法SSSA,本文提出的不动点算法FSSA均具有更快的收敛速度。也就是说,即使不考虑搜索梯度下降步长所消耗的时间,本文提出的不动点算法仍然收敛速度更快。因此,在能够准确地分离出平稳源信号的前提下,相对于Stiefel流形上的梯度下降算法,本文提出的不动点算法不需要调整梯度下降步长,收敛速度更快,耗时更少。
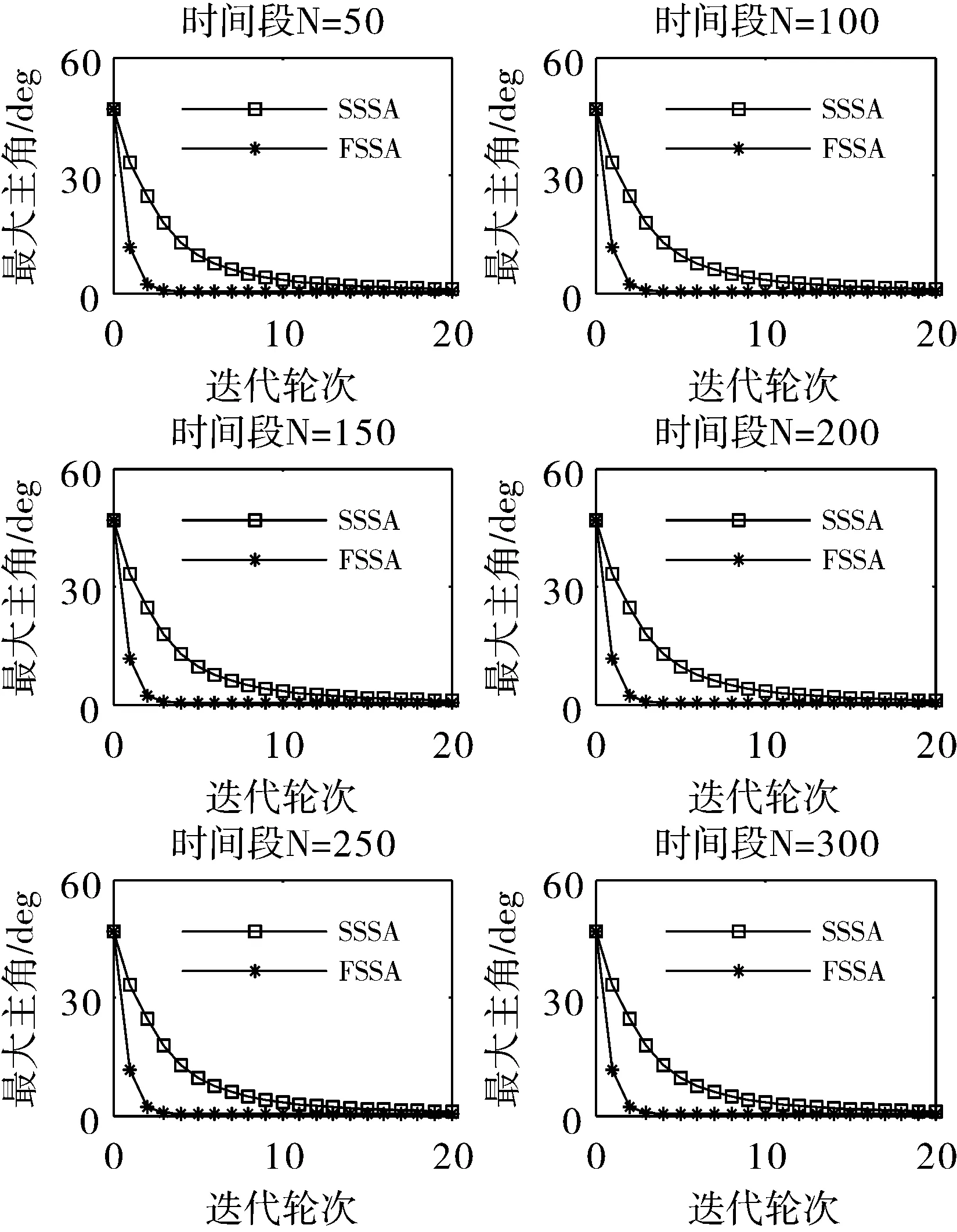
图2 仿真实验中平稳子空间分析算法的收敛速度
4 结束语
本文根据Stiefel流形上的一阶最优性条件构造了新的迭代公式,基于此迭代公式,提出了一种新的平稳子空间分析的不动点算法。仿真实验表明,由提出的算法求解得到的平稳投影与实际值之间的差异较小,可以有效地从观测到的多维非平稳信号中分离出平稳源信号,且分离精度与标准的基于Stiefel流形上梯度下降算法得到的结果相一致;相反,已有的平稳子空间分析的不动点算法分离性能不佳。
对比仿真实验的结果表明,相对于标准的基于Stiefel流形上梯度下降的平稳子空间分析算法,提出的不动点算法不需要选择梯度下降步长,收敛更快,耗时更少。
仿真实验的结果表明,需要对已有的以及本文的平稳子空间分析的不动点算法作更进一步的理论研究,包括分析迭代公式的收敛性和解的稳定性。
参考文献:
[1] Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. 2nd ed. New York: Springer-Verlag, 2009.
[2] von Bunau P, Meinecke F C, Kiraly F C, et al. Finding stationary subspaces in multivariate time series[J]. Physical Review Letters, 2009,103(21):214101.
[3] Hyvarien A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999,10(3):626-634.
[4] Shi Zhenwei, Tang Huawen, Tang Yiyuan. A fast fixed-point algorithm for complexity pursuit[J]. Neurocomputing, 2005,64(1):529-536.
[5] Fiori S. Fixed-point neural independent component analysis algorithms on the orthogonal group[J]. Future Generation Computer Systems, 2006,22(4):430-440.
[6] 龚丹丹,刘国庆. 基于极大似然Parzen窗的独立成分分析[J]. 计算机工程, 2010,36(18):279-284.
[7] 王继伟,高宝成. 一种盲信号分离算法的改进研究[J]. 计算机与现代化, 2010(2):52-54.
[8] 赵礼翔,刘国庆. 基于Givens矩阵和联合非线性不相关的盲源分离新算法[J]. 计算机科学, 2015,42(5):149-152.
[9] 陈梦,何选森. 基于八阶收敛牛顿迭代的Fast-ICA改进算法[J]. 计算机工程与应用, 2017,53(11):178-181.
[10] Hara S, Kawahara Y, Washio T, et al. Separation of stationary and non-stationary sources with a generalized eigenvalue problem[J]. Neural Networks, 2012,33(9):7-20.
[11] Blythe D A J, von Bunau P, Meinecke F C, et al. Feature extraction for change-point detection using stationary subspace analysis[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012,23(4):631-643.
[12] Zeng Hong, Song Aiguo. Removal of EOG artifacts from EEG recordings using stationary subspace analysis[J]. The Scientific World Journal, 2014,2014(2):259121.
[13] 严如强,钱宇宁,胡世杰,等. 基于小波域平稳子空间分析的风力发电机齿轮箱故障诊断[J]. 机械工程学报, 2014,50(11):9-16.
[14] 刘尚坤,唐贵基,庞彬. 基于相空间重构与平稳子空间分析的滚动轴承故障诊断[J]. 振动与冲击, 2015,34(22):187-191.
[15] Plumbley M D. Geometrical methods for non-negative ICA: Manifolds, Lie groups and toral subalgebras[J]. Neurocomputing, 2005,67(1):161-197.
[16] Absil P A, Mahony R, Sepulchre R. Optimization Algorithms on Matrix Manifolds[M]. Princeton: Princeton University Press, 2008.
[17] Box G E P, Jenkins G M, Reinsel G C, et al. Time Series Analysis: Forecasting and Control[M]. 5th ed. Hoboken: John Wiley & Sons, 2016.
[18] Wen Zaiwen, Yin Wotao. A feasible method for optimization with orthogonality constraints[J]. Mathematical Programming, 2013,142(1-2):397-434.
[19] Nocedal J, Wright S J. Numerical Optimization[M]. 2nd ed. New York: Springer Science+Business Media, 2006.

