需求干扰下的两阶段应急资源调度问题*

朱洪利，周 泓，孔继利，高德华

(1.山东工商学院 工商管理学院，山东 烟台264005；2.北京航空航天大学 经济管理学院，北京 100191；3.北京邮电大学 自动化学院，北京 100876；4.山东工商学院 管理科学与工程学院，山东 烟台264005)

0 引言

近年来，诸如地震、雪灾、洪水等自然灾害类突发事件的发生，给人民生活带来了极大的危害。我国地域面积广阔，是多种自然灾害多发的国家。当面对此类突发事件时，应急救援点的布局以及应急资源及时有效地调度，具有重要意义。

为了解决不同背景下的应急救援问题，国内外学者开始了一系列研究。钟永光等[1]对我国应急管理的战略需求和研究基础进行了阐述，并且分析了我国非常规突发事件条件下的应急管理研究进展以及未来发展趋势；Caunhye等[2]、Equi等[3]将应急资源调度问题分为以应急资源配置优化为核心和以调度车辆的路径规划为核心的2类问题，其中，应急资源的配置优化是应急资源调度的关键，其目的是为了实现应急资源在应急管理体系网络中的时空最优布局和配置；吕永波等[4]对自然灾害救援中应急资源的发放问题进行了研究，目标是有限应急资源的救助效益最大化；Linet等[5]考虑了多种运输方式，最小化总的未满足物资需求量的应急救援物资调度模型；朱建明等[6]研究了一个针对突发事件的应急医疗资源的车辆调度模型，目标是最小化全部未满足的资源需求量和总物资延迟到达医院的时间；石彪等[7]针对突发事件发生后车辆不能将应急物资一次性送达需求点的情况，研究了多次、分批运输的两阶段车辆调度问题。

考虑到应急救援问题是一个系统、复杂的科学问题，单目标优化模型难以全面地考虑实际问题，因此多目标优化的应急救援问题研究越来越多[8-9]。Tzeng等[10]考虑了确定需求条件下，最小化成本、最小化总运行时间、最大化最小满意度的多目标应急资源优化问题，并将其转化为单目标问题，用Cplex求解；陈志宗等[11]针对重大突发事件的应急选择问题，建立了相应的多目标优化模型，利用目标加权法和约束法，将问题转化为单目标问题进行求解；张玲等[12]考虑到应急资源的分级问题，建立了多需求点的多目标优化模型，通过约束法进行求解；王海军等[13]在模糊需求条件下，建立了最小化总运输时间和应急成本的双目标优化模型，通过加权法转化为单目标优化模型，之后使用Lingo软件求解；李双琳等[14]考虑应急物资的模糊需求，建立了应急物资选址和联运的双目标优化模型，并利用NAGAII求得问题的Pareto前沿面。

考虑到应急救援实际上是一个实时动态的过程[15-17]，张文芬等[18]将小波理论应用于海上应急管理领域，构建了海上突发事件应急资源动态需求概念模型；而为提高对灾害的响应能力，胡继华等[19]建立了基于实时信息的应急资源调度模型；刘亚杰等[20]针对灾后需求动态变化的特点，研究了动态环境下基于MPC的应急资源运输调度问题。在突发事件发生后，需求点以及需求点对于应急资源的需求量随时间变化，因此需要考虑改变调度方案产生的时间与成本变动量，以上现有成果均没有考虑动态过程对于原调度方案的影响，因此，本文针对应急救援过程中的动态需求干扰问题，建立应急资源的重调度模型。

1 模型建立

1.1 问题阐述

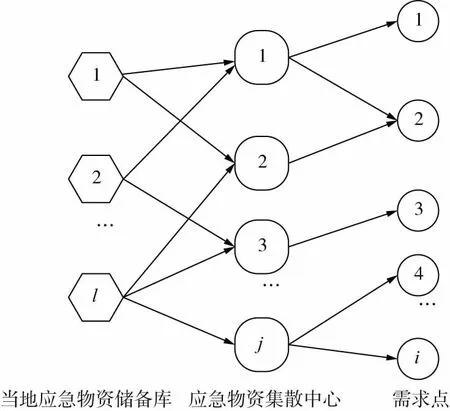
图1 三级应急物资储备调度结构Fig.1 Structure of emergency rescue

在灾害发生后，可能会面临时间紧迫、物资短缺、信息不对称、目标利益不一致等问题。特别是时间对于应急救援效果尤其重要；同时，信息的不确定性也导致相关决策活动成为一个递进动态的过程；而对于应急救援物资来说，现有储备库体系一般是分级设置的，距离受灾地点较近的当地应急物资储备库是在应急救援“黄金时间”内起到关键作用的物资供给点。而考虑当地物资储备库、应急物资集散点、物资需求点的三级储备调度结构，如图1所示，可采取“预规划-重规划”的策略以应对灾害后的需求不确定性问题。以地震为例，对于某个区域，一般会设置应急物资储备库，然后需要根据应急资源布局、综合应急成本等对应急物资集散中心进行选址规划，这一阶段处于灾害发生之前，由于没有任何需求信息，可采用一般的选址模型进行求解。但在地震发生后，由于通讯渠道受损或受限很难掌握全面的灾情信息，在开始阶段，需根据了解的基本信息进行救援，而随着救援活动的进行，各种灾情信息会逐渐汇总，会发现更多的需求点，之前预测的需求量也会发生变化；另外，余震以及次生灾害(泥石流、洪水等)的发生，也会造成需求变化。此时，需要对之前的救援方案进行修正，但是相关救援方案的调整也会造成额外的时间成本和费用成本，比如：重新装卸以及换车所需要的时间和人力成本等,故需要综合应急救援时间、救援成本、救援满意度等多种优化目标实现应急物资动态重调度。在以往的研究中，大部分模型都是考虑在灾害发生后，最优化其调度目标，譬如：时间、成本或者满意度等，大多没有考虑改变调度方案产生的时间与成本变动量。因此，本文建立一个新的两阶段应急救援模型，包括灾前的应急救援集散中心选择模型和灾害发生时的应急救援调度-重调度多目标优化模型。在调度-重调度的多目标优化模型中，时间和成本目标除了包含常规的救援时间和成本，还涉及调度方案改变后而增加的额外时间和成本；除了最大化救援满意度，在模型中还考虑到救援的公平性。因此，在灾害发生前，采用第一阶段的应急救援集散中心模型对集散中心进行布局；在灾害发生后，采用应急救援调度-重调度模型生成预调度救援方案，在需求出现干扰后，再采用调度-重调度模型进行修复，进而构建一个考虑扰动量影响的动态调度模型。

1.2 数学模型

1.2.1 模型假设

本文建立的调度模型，作以下假设：

1)所有的应急物资都由当地物资储备库运送到应急物资集散中心，再从应急物资集散中心调往各个需求点；应急物资集散中心的选取需根据平时应急物资资源布局、综合应急成本等进行选址规划。

2)允许1个应急物资集散中心向多个需求点供应物资，1个需求点也可以接收来自多个集散中心的物资。

3)当地应急物资储备库是应急救援“黄金时间”内最重要的供给点，通常出现灾情后，利用本地储备库进行快速救援，暂不考虑外地调入。

4)远程救援物资不能及时到达，资源比较紧缺，总的需求无法全部满足，定义需求点的满意度为该应急点得到的物资与所需应急物资之比。

5)政府和社会公众力量使各个供应地有足够的运输车辆，车辆的装载量一致。

6)各个应急物资储备库的供应量是已知的，灾害发生后，各个需求点的需求量可能发生变化。

1.2.2 应急救援物资集散中心选择模型

第一阶段对应“应急救援物资集散中心选择模型”，具体内容如下：

1)符号说明

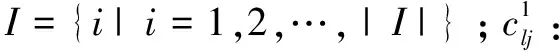
2)决策变量

xj：如果选择候选点j(j∈J)作为应急物资集散中心，则xj=1；否则，xj=0。ylj：如果当地物资储备库l(l∈L)为应急物资集散中心j(j∈J)供应物资，则ylj=1；否则，ylj=0。zji：如果应急物资集散中心j(j∈J)为需求点i(i∈I)供应物资，则zji=1；否则，zji=0。

建立如下应急物资集散中心选择模型：

(1)

上述模型中，目标函数式(1)是使得区域内救援服务的总成本最小；约束条件式(2)是保证选择p个物资集散候选点作为应急物资集散中心；约束条件式(3)保证每个当地储备库都会提供服务；约束条件(4)保证每个需求点至少有1个应急物资集散中心为其提供服务；约束条件式(5)表示，只有当候选点j被选为应急物资集散中心时，当地物资储备库才会为其提供服务；约束条件式(6)表示，只有当候选点j被选为应急物资集散中心时，它才可以为需求点提供服务；约束条件式(7)表示，如果候选点j被选为应急物资集散中心，则至少有1个当地储备库为其提供服务；约束条件(8)表示，如果候选点j被选为应急物资集散中心，则其必会为需求点提供服务；约束条件式(9)，(10)，(11)表示，变量均为0-1整数决策变量。

1.2.3 应急救援物资调度-重调度多目标优化模型

第二阶段对应“应急救援物资调度-重调度多目标优化模型”，具体内容如下：

1)符号说明

2)决策变量

ylj：调整后调度方案，当地物资储备库l(l∈L)为应急物资集散中心j(j∈JC)供应物资的数量；zji：调整后调度方案，当地物资集散中心j(j∈J)为需求点i(i∈IO∪IN)供应物资的数量；λi：需求点i(i∈IO∪IN)供应物资的满意度。

应急救援调度-重调度的多目标优化模型如下：

(12)

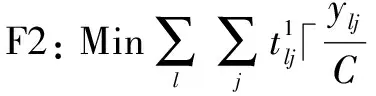
(13)

(14)

上述模型中，目标函数式(12)是使得单位物资的调配总成本最小，其中分子第1项和第2项表示运送总成本，第3项和第4项表示由于运送量改变，相应的装卸及搬运成本等；目标函数式(13)是使得总运行时间最小，前2项表示运送的总时间，后2项表示由于运送量改变带来的额外作业时间；目标函数式(14)是使得总的需求点满意度最大。通常，出现灾情后，利用本地储备库进行快速救援，远程的救援物资不能及时到达，资源比较紧缺，总的需求无法全部满足，故约束条件式(15)保证本地储备库所有的物资都进行供给；约束条件式(16)表示物资集散地的运入量等于运出量，即全部提供给需求点；约束条件式(17)表示物资需求点的供给量不超过其需求量；约束条件式(18)定义了物资需求点的满意度函数；约束条件式(19)表示决策变量约束，α为需求点的最低满意度(保证不同需求点的公平性)；「x⎤表示大于等于x的最小整数。

2 算例分析

2.1 应急救援物资集散中心选择

某地区建设有2个物资储备库、6个应急物资集散中心候选点，现有7个应急物资需求点，需要选择4个应急物资集散中心，相应的坐标位置如下：L={(1，15)，(3，5)}；J={(10，1)，(24，36)，(27，7)， (8，21)，(39，11)，(13，47)}；I={(25，2)，(32，26)，(8，49)，(36，11)，(50，19)，(27，10)，(40，25)}；建立应急物资集散中心的建设费用h={2，5，3，6，1，4}。

本文中，应急救援集散中心选择问题实际上是一个0-1整数规划问题，且目标和约束都为线性，故选用分支定界算法对问题求解。

对第一阶段模型设计分支定界算法，如图2所示，并在处理器为Intel Core Quad 2.66 GHz，内存为4G的计算机上运行程序，编程环境为Matlab R2012a。求得问题的最优解如下：x1=x3=x4=x5=1，y14=y21=y23=y25=1，z11=z36=z43=z52=z54=z55=z57=1，其他变量为0，即选择应急物资集散候选点1，3，4，5作为应急物资集散中心。

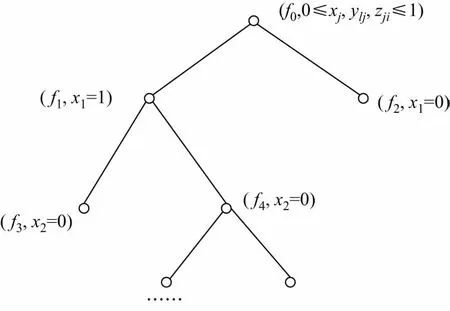
图2 分支定界算法Fig.2 Branch and bound algorithm

2.2 应急救援物资调度-重调度

在上例基础上，设该区域物资储备库的供应量s=(30，60)，需求点的需求量d=(13，24，7，12，20，8，10)。在某一时间点发现新的应急需求点IN={(9，28)，(22，39)}，dN=(17， 9)，并且需求点6新增需求量20，设车辆容量为4，最低满意度α设置为0.2。

多目标问题求解方法主要有目标加权法、约束法、评价函数法、以及多目标进化算法等。带有精英策略的快速非支配排序遗传算法(NSGAII)[21]是目前比较流行的多目标进化算法，它引入了精英策略，运行速度快，并且引入秩和拥挤度概念，保持了种群的多样性。Matlab提供的多目标遗传算法工具箱的函数gamultiobj就是NSGAII的1个变形，函数定义了最优前沿的个体在种群中所占的比例ParetoFraction, 来确定第一前端中允许保留的个体数目。对第二阶段的模型，本文利用matlab多目标遗传算法工具箱进行求解，运算的软硬件环境同第一阶段一致。

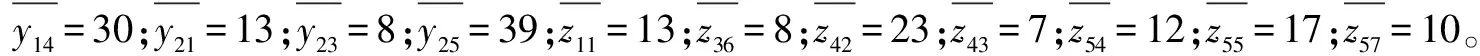
2)设置最优前沿个体系数ParetoFraction为0.3，种群大小PopulationSize为200，进化代数Generations为1 000，由于F3为最大化，转化为最小化-F3。针对新需求，利用matlab多目标遗传算法工具箱求得重调度问题的解，如图3所示。

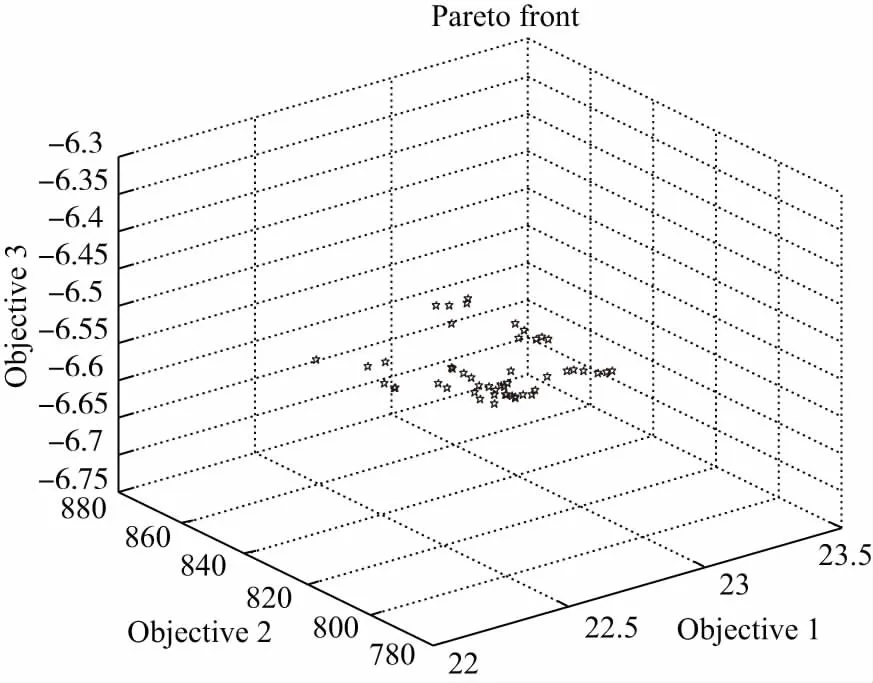
图3 目标F1-F2-F3的非劣解前沿Fig.3 Pareto front for F1-F2-F3

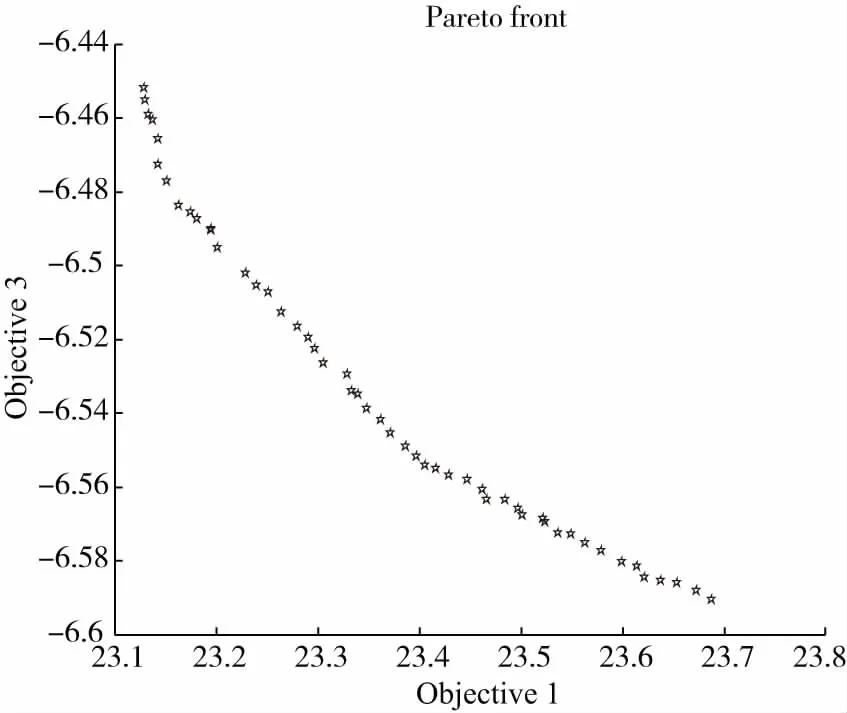
图4 目标F1-F3的非劣解前沿Fig.4 Pareto front for F1- F3

为了有效分析目标函数F1，F2，F3的关系，本文进一步分别研究F1-F3和F2-F3的双目标优化问题。实验结果如图(4)，图(5)所示。由图(4)可知，在前沿面上，调度总成本越大，相应带来的需求满意度也会越大。当总满意度低于6.48时，通过增加调度总成本可以显著提高总满意度效果。当调度总成本在点a(23.19，6.49)到点b(23.64，6.59)区间，通过增加调度的总成本，可以获得明显的满意度改善。但是，当总满意度大于6.59时，通过增加成本来提高总满意度的效果就不太显著了。以a，b点为例，点a(23.19，6.49)对应的调度方案如表1和表2所示，数据仅保留到小数点后2位。

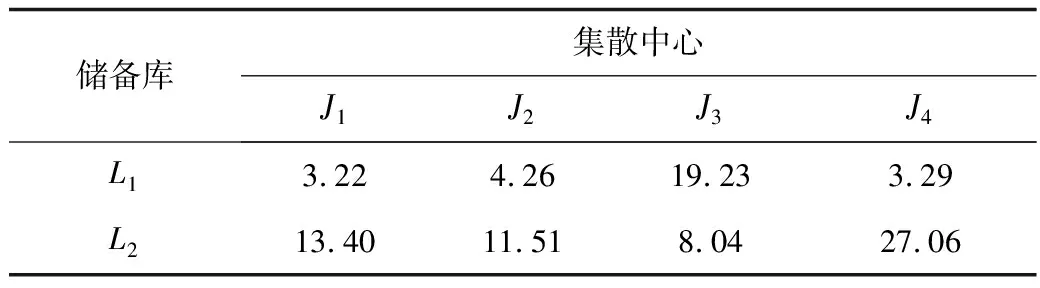
表1 点a储备库到集散中心调度方案Table 1 Schedule from storage to distribution center at a

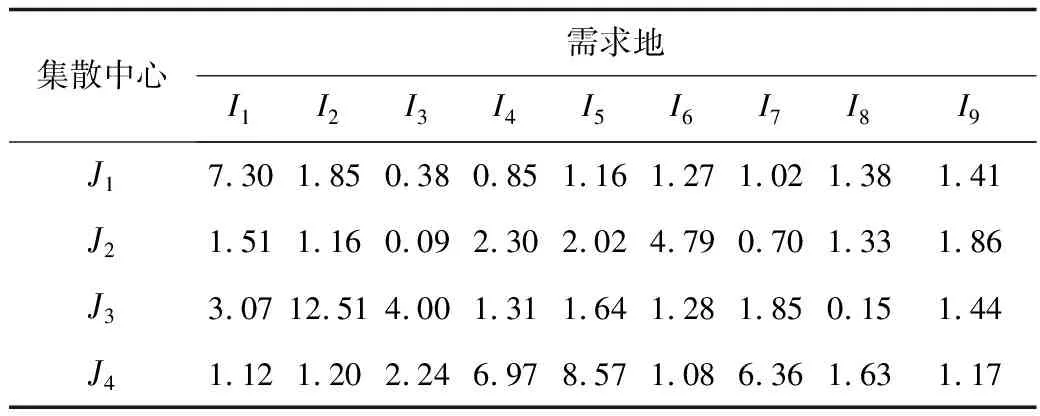
表2 点a集散中心到需求地调度方案Table 2 Schedule from distribution center to demand region at a

各个需求点的满意度分别为1.00，0.70，0.96，0.95，0.67， 0.30，0.99，0.26，0.65。

点b(23.64，6.59)对应的调度方案如表3和表4所示。

表3 点b储备库到集散中心调度方案Table 3 Schedule from storage to distribution center at b

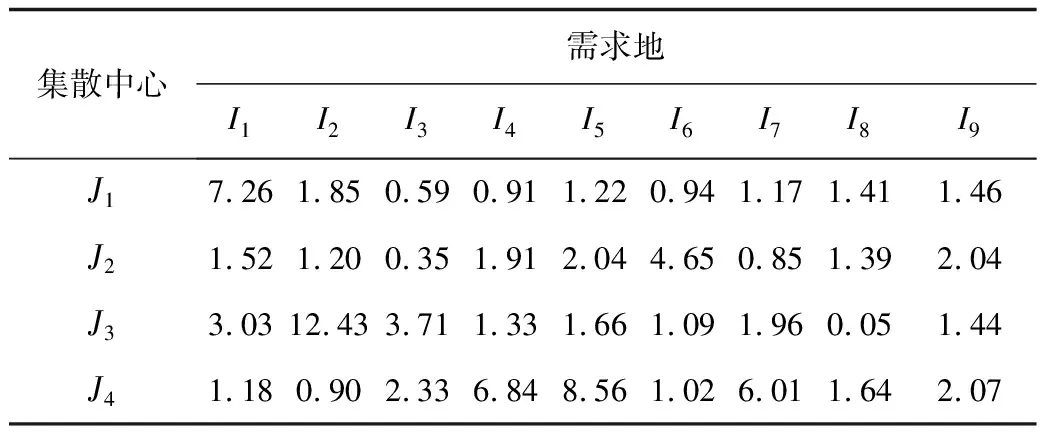
表4 点b集散中心到需求地调度方案Table 4 Schedule from distribution center to demand region at b

此时各个需求点的满意度分别为1.00，0.68，1.00，0.92， 0.67，0.28，1.00，0.26，0.78。

由表1～4可以看出，点a(23.19，6.49)到点b(23.64，6.59)的区间，从当地物资储备库到应急物资集散中心的调度量有轻微改变，但是从应急物资集散中心到需求地的调度方案中，通过增加配送成本(总成本由23.19变为23.64)，例如增加救援人员的数量、额外的车辆等，增加运往需求地I9的物资数量，减少对其他需求点的供应数量，而使得需求地I9的满意度从0.65变为0.78，而其他需求地满意度降低较小，总满意度也从6.49上升到6.59。

对于总运行时间和总满意度的关系，由图(5)可以看到，当满意度大于6.66时，如要再提高总满意度，耗费的时间也会大大增长。当在区间c(803，6.57)到d(833，6.66)时，通过增加运行的时间，总满意度可以得到明显的改进。同样，c(803，6.57)对应的调度方案如表5和表6所示。

表5 点c储备库到集散中心调度方案Table 5 Schedule from storage to distribution center at c

表6 点c集散中心到需求地调度方案Table 6 Schedule from distribution center to demand region at c

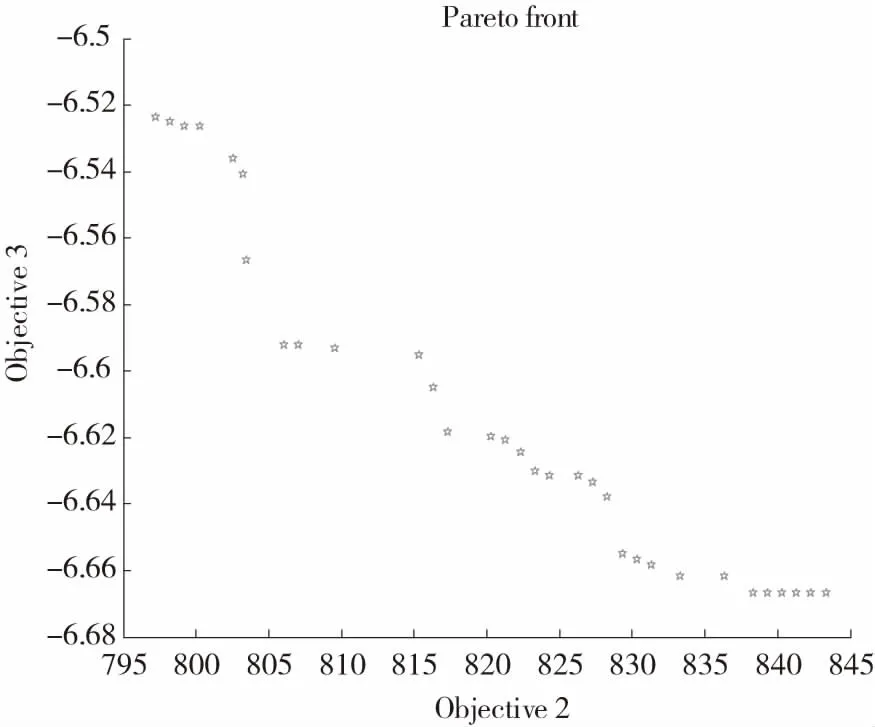
图5 目标F2-F3的非劣解前沿Fig.5 Pareto front for F2-F3

各个需求点的满意度为1.00，0.68，1.00，1.00，0.58，0.30，0.97，0.33，0.70。

点d(833，6.66)对应的调度方案如表7和表8所示。

表7 点d储备库到集散中心调度方案Table 7 Schedule from storage to distribution center at d

此时各个需求点的满意度为1.00，0.66，1.00，1.00，0.57，0.28，0.99，0.32，0.85。

由表5～8可以看出，点c(803，6.57)到d(833，6.66)区间时，通过增加总运行时间(总运行时间由803变为833)，例如增加额外的装卸以及车辆配送时间等，增加运往需求地I9和I7的数量，减少对其他需求点的供应量，而使得I7的满意度从0.97变为0.99，I9的满意度从0.70变为0.85，其他需求地的满意度降低较小。因此，总满意度也从6.57上升为6.66。

3 结论

1)针对突发事件发生时应急物资需求存在动态变化的特点，建立两阶段的应急救援模型：灾前的应急救援集散中心选择模型和灾害发生时的应急救援调度-重调度多目标优化模型。

2)对于应急救援物资集散中心选择模型，采用分支定界算法；对于应急救援物资调度-重调度模型，设计最小化总运行成本、总运行时间和最大化满意度的多目标遗传算法。

3)算例实验结果表明，所设计的遗传算法可以得到满意的Pareto前沿，决策者可以根据自身偏好来选择相应的调度-重调度方案。

[1] 钟永光，毛中根，翁文国，等.非常规突发事件应急管理研究进展[J].系统工程理论与实践，2012，32(5)：911-918.

ZHONG Yongguang,MAO Zhonggen,WENG Wenguo,et al.Progress of study on unconventional emergencies management[J]. Systems Engineering-Theory & Practice, 2012, 32(5): 911-918.

[2] CAUNHYE A M,NIE X,POKHAREL S. Optimization models in emergency logistics: A literature review[J]. Socio-Economic Planning Sciences, 2011, 46(1):4-13.

[3] EQUI L,GALLO G,MARZIALE S, et al. A combined transportation and scheduling problem[J].European Journal of Operational Research, 1997, 97(1):94-104.

[4] 吕永波, 贾楠, 任锦鸾,等. 救灾物资发放问题的动态遗传算法求解[J]. 管理科学学报, 2008, 11(3):29-34.

LYU Yongbo,JIA Na,REN Jinluan,et al. Dynamic genetic algorithm for problems of distributing goods to disaster areas[J]. Journal of Management Sciences in China, 2008, 11(3):29-34.

[5] OZDAMAR L, EKINCI E, KUCUKYAZICI B. Emergency logistics planning in natural disasters[J]. Annals of Operations Research, 2004, 129(1/4): 217-245.

[6] 朱建明，韩继业，刘德刚.突发事件应急医疗物资调度中的车辆路径问题[J].中国管理科学，2007，15(z1)：711-715.

ZHU Jianming,HAN Jiye,LIU Degang.Vehicle routing model for medical supplies in large-scale emergencies[J]. Chinese Journal of Management Science, 2007, 15(z1):711-715.

[7] 石彪，池宏，祁明亮，等.应急物资运输的两阶段车辆调度模型[J].系统工程，2012，30(7)：105-111.

SHI Biao, CHI Hong, QI Mingliang, et al.A two stage vehicle scheduling model of transportation of Emergency Resources[J]. Systems Engineering, 2012, 30(7):105-111.

[8] 王娟，聂锐，阎薪宇.多目标规划在应急物流中的应用综述[J].中国安全生产科学技术，2017，13(7)：68-73.

WANG Juan, NIE Rui, YAN Xinyu.Review on application of multi-objective programming in emergency logistics[J]. Journal of Safety Science and Technology, 2017, 13(7):68-73.

[9] 唐伟勤，邹丽，郭其云.多应急点多需求点物资调度的灰色多目标规划[J].中国安全生产科学技术，2016，12(11)：148-152.

TANG Weiqin, ZOU Li,GUO Qiyun.Grey multi-objective programming for materials dispatching from multiple supply points to multiple demand points[J]. Journal of Safety Science and Technology, 2016, 12(11):148-152.

[10] TZENG G H, CHENG H J, HUANG T D. Multi-objective optimal planning for designing relief delivery systems[J]. Transportation Research Part E, 2007, 43(6):673-686.

[11] 陈志宗, 尤建新. 重大突发事件应急救援设施选址的多目标决策模型[J]. 管理科学, 2006, 19(4):10-14.

CHEN Zhizong,YOU Jianxin.A multi-objective decision model of emergency rescue facility location for large-scale emergency incidents[J]. Journal of Management Sciences, 2006, 19(4):10-14.

[12] 张玲, 黄钧, 朱建明. 应对大规模突发事件的资源布局模型与算法[J]. 系统工程, 2008, 26(9):26-31.

ZHANG Ling,HUANG Jun,ZHU Jianming.The location and allocation model and algorithm of response to large-scale emergency[J]. Systems Engineering, 2008, 26(9):26-31.

[13] 王海军，王婧，马士华，等.模糊需求条件下应急物资调度的动态决策研究[J].工业工程与管理，2012，17(3)：16-22.

WANG Haijun,WANG Jing, MA Shihua, et al. Dynamic decision-making for emergency materials dispatching based on fuzzy demand[J]. Industrial Engineering and Management,2012,17(3):16-22.

[14] 李双琳，马祖军，郑斌，等.震后初期应急物资配送的模糊多目标选址-多式联运问题[J].中国管理科学，2013，21(2)：144-151.

LI Shuanglin,MA Zujun,ZHENG Bin, et al.Fuzzy multi-objective location-multimodal transportation problem for relief delivery during the initial post-earthquake period[J]. Chinese Journal of Management Science, 2013, 21(2): 144-151.

[15] 田军，马文正，汪应洛，等.应急物资配送动态调度的粒子群算法[J].系统工程理论与实践，2011，31(5)：898-906.

TIAN Jun, MA Wenzheng, WANG Yingluo, et al. Emergency supplies distributing and vehicle routes programming based on particle swarm optimization[J]. Systems Engineering-Theory & Practice, 2011,31(5):898-906.

[16] 王慧敏，刘高峰，佟金萍，等.非常规突发水灾害事件动态应急决策模式探讨[J].软科学，2012，26(1)：20-24.

WANG Huimin,LIU Gaofeng,TONG Jinping, et al. Study on dynamic emergency decision-making mode of unconventional water disaster[J]. Soft Science, 2012, 26(1):20-24.

[17] ZHOU Y, LIU J, ZHANG Y, et al. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems[J]. Transportation Research Part E Logistics & Transportation Review, 2017, 99:77-95.

[18] 张文芬，杨家其.基于小波神经网络的海上突发事件应急资源动态需求预测[J].运筹与管理，2015，24(4)：198-205.

ZHANG Wenfen,YANG Jiaqi.Dynamic Demand Forecast of Maritime Emergency Response Resources Based on Wavelet Neural Network[J]. Operations Research and Management Science, 2015,24(4):198-205.

[19] 胡继华，钟广鹏，严国灿.基于实时信息的动态应急资源调度模型[J].计算机应用研究，2011，28(12)：4451-4455.

HU Jihua,ZHONG Guangpeng,YAN Guocan.Dynamic emergency resources scheduling model based on real-time information[J]. Application Research of Computers, 2011,28(12):4451-4455.

[20] 刘亚杰,吴志永.灾后动态环境下基于MPC的应急运输实时调度研究[EB/OL].(2017-11-23)[2018-05-23].http://kns.cnki.net/KCMS/detail/21.1124.TP.20171123.1351.011.html.

[21] DEB K,PRATAP A,AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.