基于格子气模型的北京地铁站内人流移动分析*
王宗直,路 堃,陈 涛,姚娟娟
(1.清华大学 工程物理系 公共安全研究院,北京 100084;2.北京市地铁运营有限公司地铁运营技术研发中心 地铁运营安全保障技术北京市重点实验室,北京 102208)
0 引言
在现代都市中,地铁作为一种高效、便捷、大运力的公共交通工具,承担着城市中极其重要的交通运输任务,很大程度上缓解了大型城市地面交通拥堵的情况,为城市居民日常生活提供了很大的便利。截至2015年底,全国共有37个直辖市或地级市已经运营或正在铺设地铁线路,随着中国城镇化进程的不断发展,地铁的使用将越来越广泛,每天搭乘地铁出行的人数将不断上升。以北京地铁为例,北京地铁是全世界日均运送旅客数量最多的城市轨道交通系统,日均流量约为一千万人次,担负着北京全市大部分公共运输任务。
对于城市轨道交通运输系统来说,最重要的一项任务就是保护旅客生命安全,虽然自伦敦地铁投入使用以来,全世界范围内地铁事故发生概率都极小,但是依然存在一定的安全风险。除了恶意破坏和设备故障两大事故诱因外,人流量过大导致的人群密集、拥塞对轨道交通公共安全也带来了极大的挑战。尤其在中国都市中,人口密度极大,导致地铁站内拥挤的情况也较为严重,存在一定的安全隐患。
针对这一问题,本文提出了基于格子气模型的地铁站内人流移动模型,通过数值模拟的方式,预算站内人流拥堵情况,通过可视化的输出结果显示站内人群的在未来某一时刻内的分布情况以及关键位置发生拥堵的情况,实现预测预警功能。
1 使用模型
本文在格子气模型的基础上,根据地铁站台实际情况,以闸机作为分界点,搭建站内人流移动模型。基本思想为利用蒙特卡罗方法,结合人群移动特性与统计学方法,利用实证数据修正模型参数,得到精确性符合要求的人群移动模型。
1.1 模型原理
在本文工作中使用的模型以格子气模型为基础,这一模型是由Muramatsu和Nagatani等[1-2]将扩散限制凝聚(DLA,Diffusion Limited Aggregation)模拟中的模型应用到行人流中而搭建起来的。在这一模型中,首先要将研究区域进行离散化处理,分成W×L的矩阵,将行人抽象化为服从一定游走规律的随机游走粒子进行处理,其满足的移动规则如图1所示。图中,圆点表示即将移动的行人,图中箭头以及其上标注的概率表示可能移动方向和移动概率,被交叉覆盖的格点表示被其他行人或障碍物占据,不能向其移动。这一模型满足周期性边界条件,从一侧离开矩阵的行人将会从另一侧重新进入,专门用于分析通道通行效率。

图1 格子气模型移动规则范例Fig.1 Example of moving regulation of lattice gas model
格子气模型在应用过程中也由研究者进行了一系列改进,为了解决格子气模型移动速度离散化的问题,Jiang[3]另外引入一组概率以描述行人在一个时间周期内跨越2个格点的情形,通过调整概率大小可以实现移动速度的变化,使用改进后的模型对通道通行效率进行了分析;随着格子气模型的发展,格点转移也逐渐复杂,力求能更好地模拟行人运动,引入Moore型和扩展的Moore型转移方式,但这2种转移方式都会出现实际直线距离较短、程序模拟路径较长的情况; Guo[4]提出了圆形概率转移模型,解决了这一问题;在此基础上,Hartmann[5]提出了六边形格子气模型,兼顾了行人路径选择、路径距离的一致性和编程上的便利性,在近几年逐渐被人重视并采用;Yu[6],Zheng[7]等将格子气模型与实际结合,利用该模型研究了房间内的人群疏散问题;在此基础上,学者们针对人群信息传递[8]、路径选择[9-10]、拥堵[11-12]以及在国内场景中的实际应用[13-15]进行了研究。本文利用动态参数的格子气模型进行建模计算,因其需要设置每一处概略分布矩阵的值,设置参数过程较繁琐,故编程工作量大,作为离散性的模型,格子气模型在移动概率矩阵变化处的连续性较差,但是,此算法逻辑较连续性模型简单,能够保证一定的精确度和运算速度,比较适合用于解决本文中提出的快速短时人流模拟问题。
1.2 建模过程
本文以北京地铁五号线与十号线的换乘站——惠新西街南口站作为研究对象,该站位于北京东北部,处在北三环与北四环之间,是重要的地铁交通枢纽,也是北京地铁最繁忙的站台之一,建站以来人流压力很大,一直通过更改部分扶梯上下行的方向、高峰期采取限流措施等方式对站内人流进行疏导。2014年11月07日,在该站由于过度拥挤发生了1起车门事故,造成了1名乘客死亡。因此,对该站台进行研究具有很强的必要性与代表性。
惠新西街南口站站内设施较少,通过闸机进站后仅有2层,分别为位于地下一层的地铁十号线站台和位于地下二层的地铁五号线站台。闸机口均设置在地下一层,是北京地铁站台设计中较少的进站后不需上下楼即可直接乘车的地铁站之一。五号线站台设计上和十号线站台垂直,位于十号线站台的正下方,通过一段楼梯或扶梯就可以实现换乘,换乘时间大约为30 s,换乘时间很短。
本文在惠新西街南口站施工平面图的基础上,以闸机口为边界,将站内行人可以到达的区域进行网格化处理,共建模区域面积4 040 m2。考虑到站台整体情况,负一层为十号线侧式站台,将其划分为南北2个模块,负二层为五号线岛式站台,将其整体划为1个模块,因此,将整个站台划分为3个模块进行处理。模块内采取网格化的模式建模处理,模块之间利用通道相连,通道内情况较单一,通过测算移动速度与通道长度,给出行人在通道中的转移时间。
1.3 模型假设
为编写算法的需要,除格子气模型基本假设外,结合站台实际情况,对人流特性额外做出了一系列假设:
1)模型对分析区域进行了网格化划分,每一个网格的大小为0.5 m×0.5 m,每1个行人占据1个网格;
2)人群移动速度约为1.5 m/s,相对应地,模型3个时间步长对应实际运动时长为1 s;
3)在没有阻碍的情况下,每个行人优先选择的路线一定是符合其效益最大化原则的,并且每个行人清楚地知道自己的目的地以及前往该目的地最短的路线;
4)在行人进入模型时,使用蒙特卡罗方法确定其目的地,并认为在应用模型的过程中,行人出发-到达选择(O-D对)概率分布在短时间内不变;
5)不考虑列车满员无法上车的情况,并简化了乘客对屏蔽门的选择过程,只考虑下车人流从屏蔽门进入站台,没有设计上车乘客的上车排队过程;
6)从地下二层前往地下一层2个模块的人群全部通过扶梯进行模块之间的转移,没有行人会选择楼梯进行上行的换乘。
1.4 算法逻辑

图2 算法流程Fig.2 Algorithm flow chart
在本程序中所采用的算法流程图如图2所示,程序开始运行后,先完成矩阵和变量的初始化,在这一阶段预设各个闸机口和列车屏蔽门进入站台的人流情况、设置程序运行的时间周期,随后进入时间周期循环。在每一个循环内,对网格化的站内各个格点进行分析,调取概率转移矩阵,利用蒙特卡罗方法模拟实际的移动情况,将1个时间周期内每个格点都计算完成后进入下一个格点的分析。
2 初步模拟与实证分析
2.1 输出范例
程序输出界面如图3所示,其中每一个不同颜色的格点表示目的地不同的行人,利用图形界面,直观地输出程序运行结果。图中黑色部分为站台及站厅中乘客不可到达的区域或通往其他模块的通道区域,深色部分为建模区域,乘客可以在其中按移动规则进行移动,浅色方块代表行人。

图3 程序输出结果界面Fig.3 The output interface of the algorithm
2.2 实证研究
为了确定模型中的各项参数,在模型基本框架搭建完成后,制定了实验方案,组织实验人员赴惠新西街南口站进行1次实地实验。进行此次实验的目的主要有以下4点:
1)验证模型中各项移动参数的准确性;
2)对站台内部行人O-D对进行记录;
3)测量闸机、扶梯、楼梯的最大人流量;
4)拍摄视频资料用于模型精确度分析。
通过实地考察,得到各个通道的最大通行效率、通道通过时间、下班高峰期行人O-D对数据、现场视频资料等重要数据。
2.3 模拟结果与实证对比
利用在现场采集得到的同步视频,对视频进行后处理以进行模型精确度分析,具体操作方式为将视频中录制得到的各个通道出入口的人流情况输入对应描述通道人流的矩阵中,运行程序,可以得到程序在各个关键通道、节点人流拥塞的情况,记录模型中人流开始拥塞和拥塞结束的时刻,和视频中实际产生拥塞的时间对比,间接确定模型的精确性程度,如表1所示。
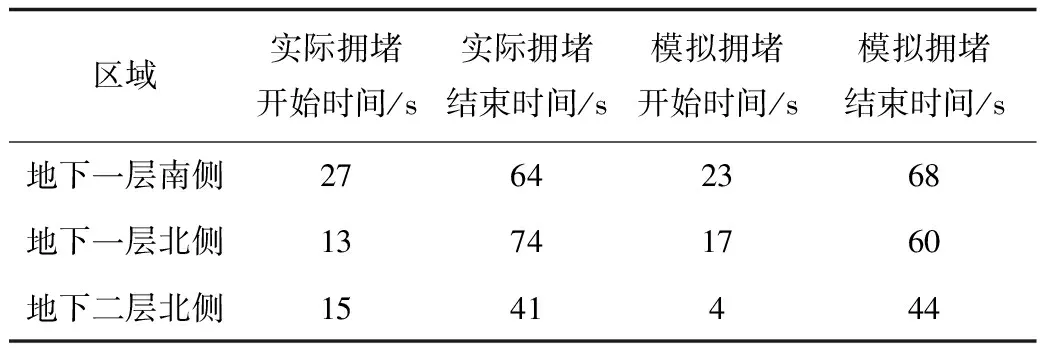
表1 模拟结果与实际结果对比Table 1 The comparison of simulation result and actual result
运行结果表明,在地下一层南侧和地下一层北侧模块中,模拟结果吻合较好,在地下二层的模拟与实际结果差别较大。精确度不足的原因主要是地下二层的地形相对较复杂,视野容易受阻,下车人流需要经过一段时间确定路线,导致了在实际过程中人流移动更加平滑,不容易产生拥堵,而程序中假设了行人清楚自己的路线选择,下车的一瞬间就开始朝一个目的地移动,导致了拥堵发生时间较早;在地下一层中,下车屏蔽门正对换乘通道,行人很容易确定其应该前进的方向,所以程序的这一假设符合的情况较好,开始拥堵的时间估计较为准确。拥堵结束的时间比较准确,是由于拥堵结束时,拥堵在通道入口处的人流基本上都通过通道转移,其通过时间和通道最大通行效率密切相关,因此,拥堵结束时间的准确性结果也证明了实验测量所得通道最大通行效率数据的准确性。对于这一特定情形,综合模型平均误差控制在5 s以内。
3 人流移动模拟
3.1 拥堵情况分析

图4 站台关键位置拥堵时间与人流量的关系Fig.4 Relation of congestion and pedestrian volume at key location
利用模型精确度较好的模块对站内关键位置进行拥堵分析,结果如图4所示。一次列车进站人流量超过70 人就可能发生拥堵,尤其在换乘通道入口处,随着人流量增大,拥堵时间逐渐增大。主要原因是换乘通道的通过能力有限,不能完成短时间大规模人流的移动,在通道入口处存在一定的安全隐患。
针对目前站台换乘通道通行效率不足的问题,探讨如果设计伊始将通道适当加宽对站内通行能力的提升作用。对模型中与通道宽度变动相关的部分的转移概率矩阵进行修改,将站台布局进行一定变动,重复进行列车进站人流量对拥堵时间的影响分析。
考虑将换乘通道增宽2 m对车站拥堵情况的影响,控制进站人流情况相同,得到拥堵时间变化情况如图5所示。从图中曲线变化情况可以看出,将站台拓宽后,不仅拥堵承载能力得到提升,在拥堵发生后,站台拥堵持续时间缩短,站台整体通行效率得到很大的提升,拥堵时间-人流曲线整体下移趋势明显。
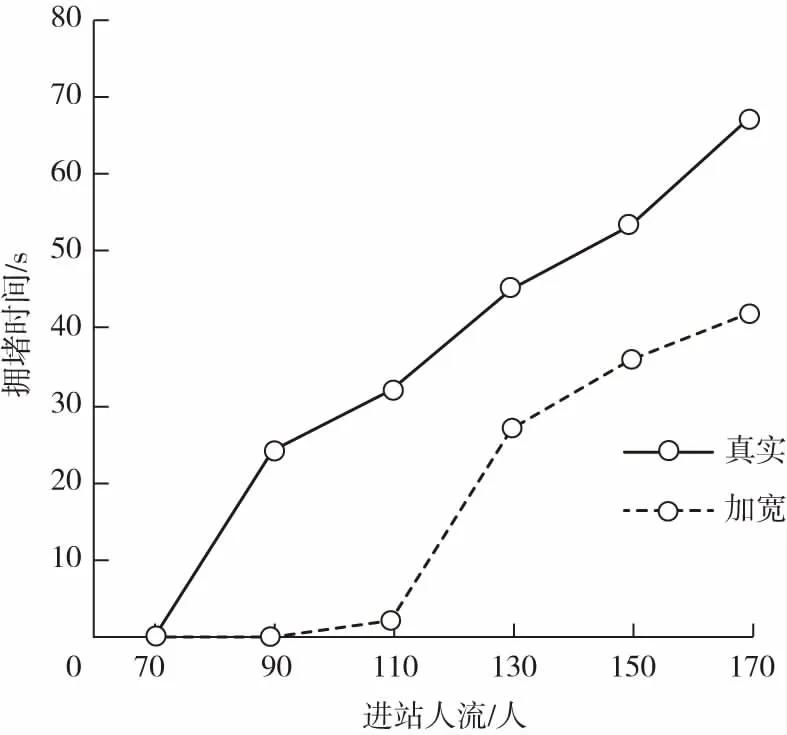
图5 通道扩宽与现有设计通行能力对比Fig.5 Comparison of traffic capacity between widened and actual passageway
将通道扩宽后,在人流量较少时的缓解拥堵的变化十分明显,能够将站台保持顺畅通行的人数上限从70人/车次提升到110人/车次。对比用于调试模型在下班高峰期拍摄到的视频资料,车站在工作日下班高峰期间某次列车到站下车人次约为120人/车次,所以将通道扩宽2 m就可以基本满足车站换乘需求。
3.2 安全提升建议
对模型运行结果进行分析,惠新西街南口站在设计伊始没有充分考虑站内人流情况,对换乘人流量估计不足,导致设计换乘通道过于狭窄,不能满足站内人流进行快速换乘的需求,建议在未来规划相似换乘布局时,适当拓宽站台换乘通道的宽度,并将较低一层的岛式站台的宽度也适当加宽,从源头缓解站台拥堵情况。
对于包括惠新西街南口站以内的北京地铁人流密集站台,由于设计上已经存在一定的缺陷,所以会在人流高峰时期通过临时设置的隔离栏改变站内地形,起到控制人流移动模式的作用,保障乘客安全;或是在特殊时期(如公众假期或特殊活动时期)关闭某些站台,采取地铁列车过站不停车的方式缓解站台压力。这些策略有一定的效果,但是对地铁的运营效率和便利性造成了很大的影响,所以,应当尽可能地减短限流措施或封闭站台措施的时间,提高地铁系统的运行能力和旅客的整体乘车体验,在站台建设已经无法更改的情况下,利用本模型提前分析站台的拥堵情况,在从10号线换乘5号线单次列车人流量超过某个阈值(如90~110人)后,决定采取相关安全措施,尽可能在保证安全的前提下减少车站限流措施。
4 结论
1)北京地铁惠新西街南口站站台设计中存在部分不足与缺陷,主要不足为十号线与五号线之间换乘通道设计通行能力较低,导致拥堵发生在换乘通道口,存在一定的安全隐患。
2)如果在前期设计中将换乘通道拓宽2 m,能够使车站通行能力大大提高,基本满足目前该站在工作日下班高峰期的换乘需求。
3)在未来地铁换乘站类似设计方案确定前,可以应用本模型的参数,搭建规划站台人流移动模型,合理估计站台人流量,模拟测试站台通行能力。
4)未来模型有望整合北京市轨道交通大数据平台,获取地铁闸机数据、摄像头影像数据、列车运行情况数据等,不断完善模型精确度,增强模型功能。目前模型已经搭好框架与算法部分,只需要获得更加精确的输入数据,或者结合大数据预测算法获得的其他数据,就可以对站内情况进行更广泛准确的研究。
[1] MURAMATSU M, IRIE T, NAGATANI T. Jamming transition in pedestrian counter flow[J]. Physica A Statistical Mechanics & Its Applications, 1999, 267(S 3-4):487-498.
[2] MURAMATSU M, NAGATANI T. Jamming transition in two-dimensional pedestrian traffic[J]. Physica A Statistical Mechanics & Its Applications, 2000, 275(1-2):281-291.
[3] JIANG R, WU Q S. Pedestrian behaviors in a lattice gas model with large maximum velocity[J]. Physica A Statistical Mechanics & Its Applications, 2007, 373(36):683-693.
[4] GUO R Y, HUANG H J. A mobile lattice gas model for simulating pedestrian evacuation[J]. Physica A Statistical Mechanics & Its Applications, 2008, 387(2-3):580-586.
[5] HARTMANN D. Adaptive pedestrian dynamics based on geodesics[J]. New Journal of Physics, 2010, 12(4):1155-1208.
[6] YU X, CHANG R, ZHANG C. Evacuation of pedestrians using lattice gas model and floor field model[C] //International Conference on Audio, Language and Image Processing, IEEE, 2015.
[7] ZHENG Y, XI X, ZHUANG Y, et al. Dynamic parameters cellular automaton model for passengers in subway[J]. Tsinghua Science and Technology, 2015, 20(6): 594-601.
[8] HAN Y, LIU H. Modified social force model based on information transmission toward crowd evacuation simulation[J]. Physica A: Statistical Mechanics and its Applications, 2017(469): 499-509.
[9] PEREIRA L A, BURGARELLI D, DUCZMAL L H, et al. Emergency evacuation models based on cellular automata with route changes and group fields[J]. Physica A: Statistical Mechanics and its Applications, 2017(473): 97-110.
[10] ANTONINI G, BIERLAIRE M, WEBER M. Discrete choice models of pedestrian walking behavior[J]. Transportation Research Part B: Methodological, 2006, 40(8): 667-687.
[11] PEREIRA L A, DUEZMAL L H, CRUZ F R B. Congested emergency evacuation of a population using a finite automata approach[J]. Safety science, 2013, 51(1): 267-272.
[12] YANG X, DONG H, YAO X. Passenger distribution modelling at the subway platform based on ant colony optimization algorithm[J]. Simulation Modelling Practice & Theory, 2017(77):228-244.
[13] 史聪灵, 钟茂华, 张岚,等. 地铁换乘车站客流疏运模拟及风险分析(2)——单通道换乘车站[J]. 中国安全生产科学技术, 2011, 7(8):21-28.
SHI Congling, ZHONG Maohua, ZHANG Lan, et al. Simulation and risk Analysis on passenger transportation of metro transfer station(2)——Single passage transferring Station[J]. Journal of Safety Science & Technology, 2011, 7(8):21-28.
[14] 陈海涛, 刘占, 靳红雨,等. 双出口疏散吸引区域模型建立与模拟分析[J]. 中国安全生产科学技术, 2017, 13(7):55-61.
CHEN Haitao, LIU Zhan, JIN Hongyu, et al. Modeling and simulation analysis on evacuation attraction region model for double exits[J]. Journal of Safety Science & Technology, 2017, 13(7):55-61.
[15] YE J, CHEN X, JIAN N. Impact analysis of human factors on pedestrian traffic characteristics[J]. Fire Safety Journal, 2012(52):46-54.

