基于演化博弈理论的合资铁路投融资问题研究
陈志明
(中国铁路总公司 办公厅,北京 100844)
0 引言
随着我国铁路的快速发展,以高速铁路、重载铁路、快速客运铁路为主的合资铁路发展迅速。截至 2016 年底,我国共有 210 家合资铁路公司,由中国铁路总公司控股的有 176 家,其中开通运营的共计 136 家,资产总额 3.52 万亿元,营业里程达到 4.38 万 km[1]。但是,在合资铁路高速发展的背后,一些合资铁路公司及其投资者面临经济效益不佳甚至是亏损的局面[2]。我国于 2016 年修订并公布的《中长期铁路网规划》提出,到 2020 年,全国高速铁路通车里程提高到 3 万 km,铁路运营里程将增长到 15 万 km,各地区合资铁路的投融资压力将倍增[3]。
关于合资铁路公司投融资问题,张新玫[4]提出合资铁路公司普遍存在债务负担过重、融资渠道窄小、投资回报率较低等问题;徐微[5]以中国铁路财务有限责任公司为例,从拓宽铁路融资渠道等方面对铁路企业开展融资租赁业务进行了分析;祝雪颖[6]基于博弈理论分析合资铁路经营管理体制并提出建议,以改变合资铁路运营亏损现状;郭经纬等[7]通过建立合资铁路融资管理均衡博弈模型,结合实例提出债券融资是一些合资铁路项目的偏好选择。从以上分析可以看出,部分研究采用传统博弈理论与方法对合资铁路公司合作关系进行分析,但却忽视了合资各方投融资行为的复杂利益关系。为此,在铁路进行混合所有制改革背景下,基于演化博弈理论对合资铁路公司投融资行为进行理论分析与仿真验证,提出改善合资铁路投融资决策行为的对策,为我国合资铁路投融资模式创新发展提供借鉴与启示。
1 合资铁路投融资问题描述与参数设定
1.1 问题描述
(1)股权主体。铁路在探索股权投资多元化的混合所有制改革过程中,明确表明国有铁路对铁路资源与铁路资本的掌控能力[8],因而必须确保国有铁路的主体地位。因此,铁路是合资铁路公司股权合作行为的发起者,占主导地位,参与投资的地方政府或者企业是跟随者。
(2)收益分配。铁路与地方政府之间依据所占合资铁路公司股额比例,合理分配各自收益。
(3)两两博弈。铁路在进行合资铁路建设项目投融资时,假定在每次博弈过程中限定博弈主体分别为铁路和地方政府。
当合资铁路公司处于项目投融资前期运营设计阶段时,铁路会选择“融资”策略或者“不融资”的策略;同时,地方政府可能会选择“投资”的策略或者“不投资”的策略。铁路与地方政府博弈的策略组合如表 1 所示。

表 1 铁路与地方政府博弈的策略组合Tab.1 The strategies applied in the game playing between the railway companies and local governments
1.2 参数设定
根据铁路与地方政府演化博弈问题描述,将有关参数做以下定义:假设铁路在出资总额中所占的比例为 α,地方政府在出资总额中所占的比例为 1-α,且铁路是合资铁路建设项目投融资行为的发起者,假设铁路出资总额大于地方政府出资总额,并且 0.5<α<1。UZT为铁路的收益函数;UKD为地方政府的收益函数。R1为铁路的基础收益;R2为地方政府的基础收益。ΔR 为铁路针对合资铁路项目建设实行融资行为,同时地方政府采取投资策略时所产生的增值收益。C1为铁路在实行融资行为后,在参与合资铁路公司建设与运营管理、设施设备维护等方面所支出的费用;C2为地方政府在投资入股合资铁路项目后参与合资铁路公司运营管理等方面所支出的费用。F2为当一方选择融资(不融资)而另一方选择不投资 (投资) 时产生的声誉成本。
为了研究方便,假定以上参数所代表的数值均为正数。
2 合资铁路投融资博弈模型构建
2.1 收益函数
假设铁路一方选择“融资”策略的比例为 x,选择“不融资”策略的比例为 1-x,其中 0≤ x≤1;地方政府选择“投资”策略的比例为 y,选择“不投资”策略的比例为 1-y,其中 0≤y≤1。构建铁路与地方政府的收益矩阵如表 2 所示。

表 2 铁路与地方政府的收益矩阵Tab.2 The prof i t matrix of the railway companies and local governments
2.2 期望收益
铁路选择“融资”策略的期望收益 UZ1为

铁路选择“不融资”策略的期望收益 UZ2为

铁路的平均期望收益为

铁路选择“融资”策略比例 x 的复制动态方程为
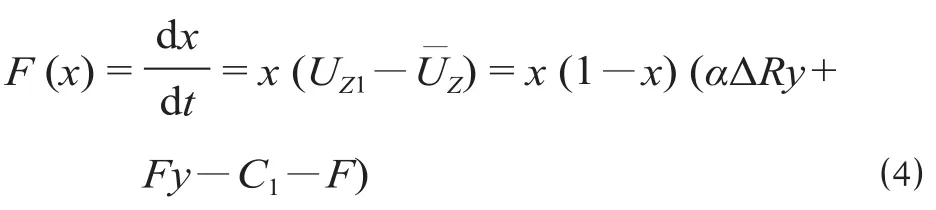
同理,地方政府选择“投资”策略比例 y 的复制动态方程为
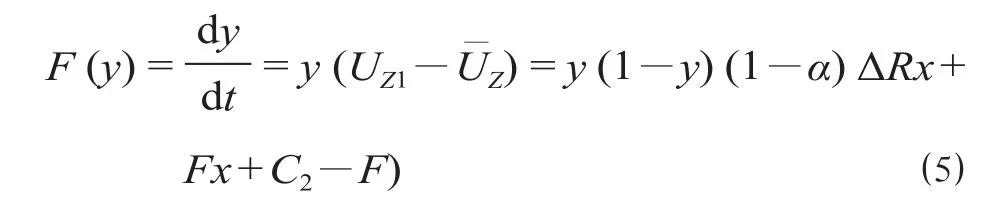
根据上述内容,得到铁路与地方政府合作系统的雅克比矩阵为

雅可比矩阵行列式的值为
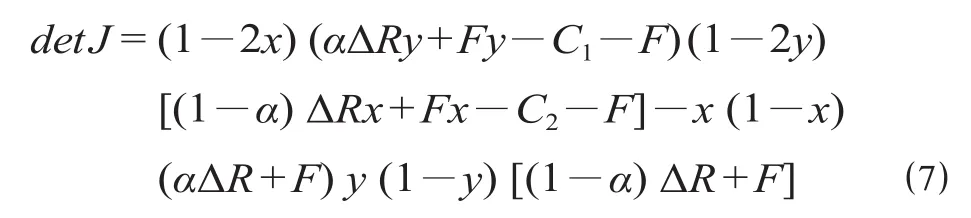
雅可比矩阵的迹为
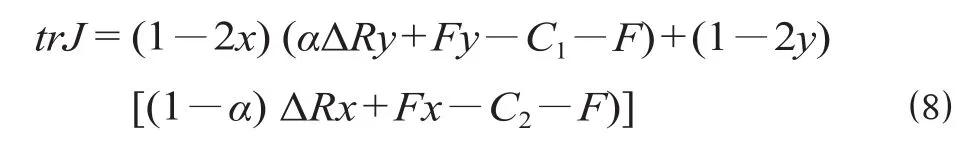
构建二维连续动态系统
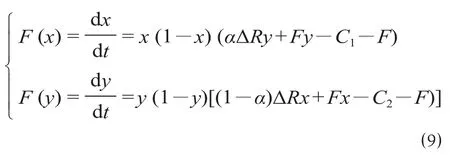
2.3 模型分析
令,则有 x = 0,x = 1 或 y =复制动态系统共有 5 个演化均衡点分别为 A (0,0),B (0,1),C (1,0),系统局部稳定性分析如表 3 所示,合资铁路系统演化相位图如图 1 所示。

表 3 合资铁路系统局部稳定性分析Tab.3 Local stability analysis of the joint-venture railway system
由图 1 可知,铁路所获得的增值收益大于其支出成本,地方政府所获得的增值收益也大于其支出方还是左下方。
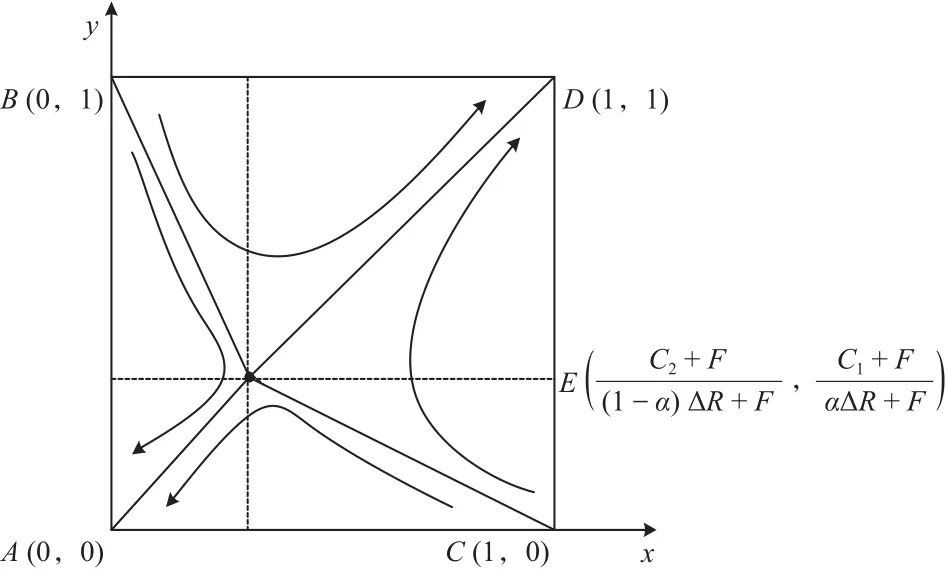
图 1 合资铁路系统演化相位图Fig.1 The phase diagram of the joint-venture railway system’s evolution
假设铁路和地方政府所选择的策略组合为时,铁路和地方政府最终会选择不融资和不投资的成本。铁路和地方政府采取何种策略取决于所选择的策略组合处于折线 BEC 的右上铁路和地方政府终会选择融资和投资的策略;显然点 E′ (x*,y*) 是影响策略选择的最终分界点。因此,为推动铁路和地方政府走向合作筹资建立合资铁路公司,应设法扩大区域 DBEC 的面积。
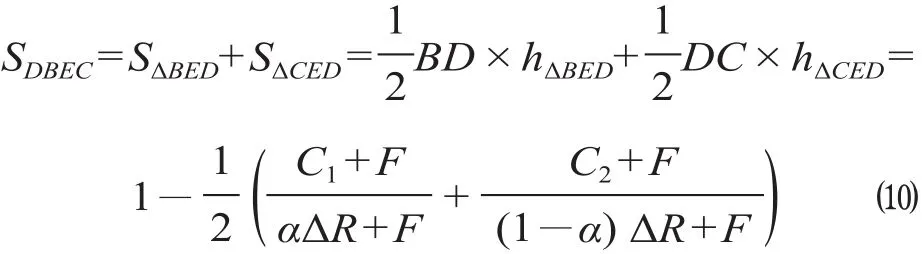
铁路选择融资策略,同时地方政府选择投资策略的概率为
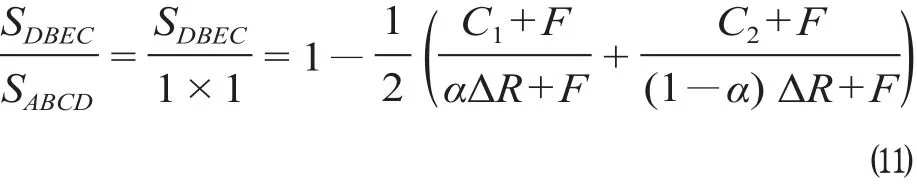
显然,当 DBEC 区域的面积越大,铁路与地方政府采取股权合作的概率也就越大。对影响其变化的各项参数求导得

由上述 2 个公式可知,铁路和地方政府在实行投融资合作后,二者参与合资铁路公司运营管理所支出的成本与 SDBEC成反比。
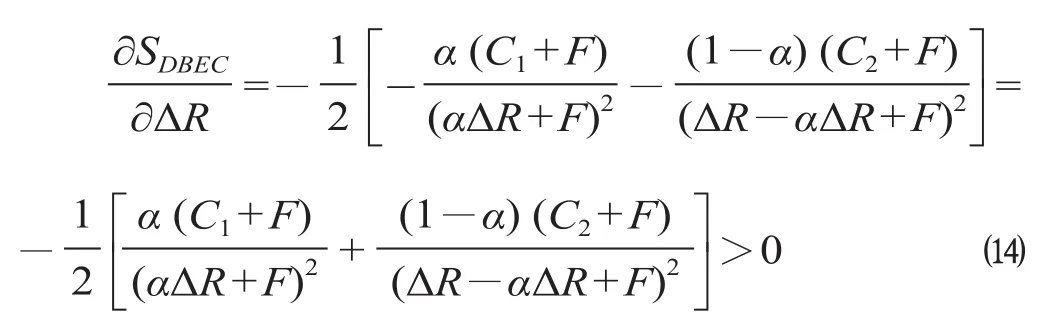
由公式 ⒁ 可知,铁路和地方政府在实施投融资合作后,所获得增值收益与 SDEBC成正比。即二者所获得的增值收益越高,区域 DBEC 的面积就越大,系统继续实现投融资合作模式的可能性也就越高;二者所获得的增值收益越低,区域 DBEC 的面积就越小,合资铁路系统继续实现投融资合作模式的可能性也就越低。

由公式 ⒂ 可知,铁路和地方政府实行投融资合作模式后,二者所占股权的份额与 SDEBC成正比。
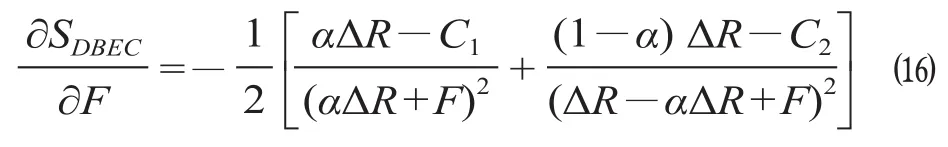
由公式 ⒃ 可知,铁路和地方政府在实行投融资合作模式后,所产生的声誉成本与 SDEBC的关系,与增值收益和运营管理成本有关。具体分析路和地方政府在实行投融资合作模式后,所产生的声誉成本与 SDEBC成反比。即所要支付的声誉成本越高,区域 DBEC 的面积就越小,合资铁路系统继续实现投融资合作模式的可能性也就越低;当所支付的声誉成本越低,区域 DBEC 的面积就越大,系统继续实现投融资合作模式的可能性也就越高。②αΔR<C1,(1-α) ΔR>C2。③αΔR>C1,(1-α) ΔR<C2。④αΔR<C1,(1-α) ΔR<C2。
当出现②,③,④ 3 种情况时,铁路和地方政府都以追求自身利益最大化为发展目标。因此,当自身利益受损后,二者会在以后的合作过程中不断学习和模仿,最终使合资铁路项目趋于不实行投融资合作的状态。
3 合资铁路投融资仿真模拟
借助 MATLAB 软件,运用数值仿真的方法,通过动态演化图对上述推论作进一步验证。演化图中横轴表示时间 t,纵轴表示概率 P。
(1)初始合作意愿变化对演化结果的影响。假定仿真参数取值分别为:ΔR = 10,C1= 3,C2= 2,F = 1,α = 0.6。对 x 和 y 分别取 2 组值,合资铁路系统仿真结果分别如图 2 和图 3 所示。仿真结果验证了初始意愿变化会影响路径演化结果的推论。在上述条件下 E 的坐标为 (0.6,0.57),此时,铁路和地方政府的初始合作意愿处于折线 BEC 的右上方时,二者最终趋于投融资合作。
(2)合资铁路公司生产运作管理成本变化对演化结果的影响。假定仿真参数取值分别为:ΔR = 10,F = 1,α = 0.6,x = 0.73,y = 0.82。对 C1和C2分别取 2 组值时,合资铁路系统仿真结果分别如图 4 和图 5 所示。仿真结果验证了在其他条件不变的情况下,合资铁路公司生产运营管理成本越高,铁路和地方政府越不倾向于投融资合作。
(3)增值收益变化对演化结果的影响。假定仿真参数取值分别为:C1= 3,C2= 2, F = 1,α = 0.6,x = 0.41,y = 0.53。对 ΔR 分别取 2 组值时,合资铁路系统仿真结果分别如图 6 和图 7 所示。仿真结果验证了在其他条件不变的情况下,增值收益越高,铁路和地方政府越倾向于投融资合作。

图 2 数值组 1 仿真结果Fig.2 The results of simulation group 1
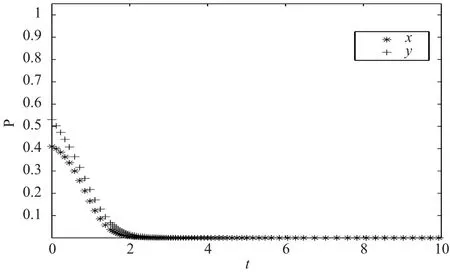
图 3 数值组 2 仿真结果Fig.3 The results of simulation group 2
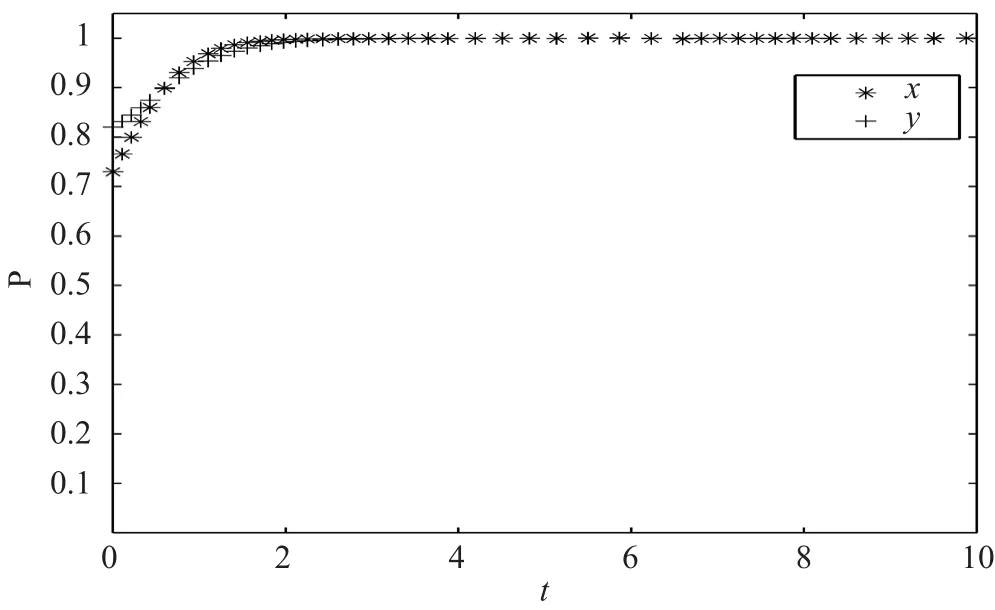
图 4 数值组 3 仿真结果Fig.4 The results of simulation group 3
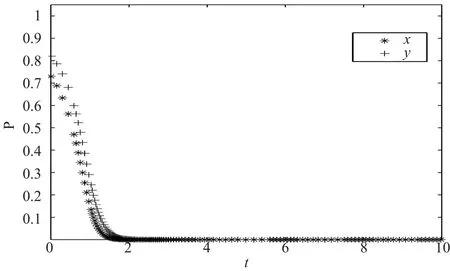
图 5 数值组 4 仿真结果Fig.5 The results of simulation group 4
(4)投融资份额变化对演化结果的影响。假定仿真参数取值分别为:ΔR = 10,C1= 3,C2= 2,F = 1,x = 0.73,y = 0.82。对 α 分别取 2 组值时,合资铁路系统仿真结果分别如图 8 和图 9 所示。仿真结果验证了在其他条件不变的情况下,地方政府外部投资公司所占投资份额越大,趋向投融资合作的速率越快。
(5)信誉成本变化对演化结果的影响。假定仿真参数取值分别为:ΔR = 10,C1= 3,C2= 2,a =0.6,x = 0.73,y = 0.82。对 F 分别取 2 组值时,合资铁路系统演化结果分别如图 10 和图 11 所示。仿真结果验证了在其他条件不变的情况下,声誉成本越大,铁路和地方政府越不倾向于投融资合作。

图 6 数值 5 仿真结果Fig.6 The results of simulation group 5

图 7 数值 6 仿真结果Fig.7 The results of simulation group 6

图 8 数值 7 仿真结果Fig.8 The results of simulation group 7
4 合资铁路投融资对策
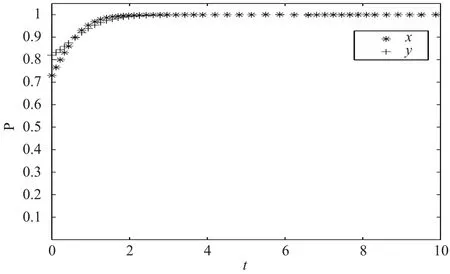
图 9 数值 8 仿真结果Fig.9 The results of simulation group 8
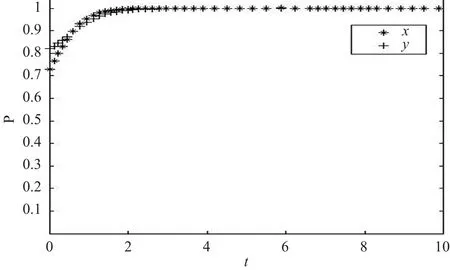
图 10 数值 9 仿真结果Fig.10 The results of simulation group 9
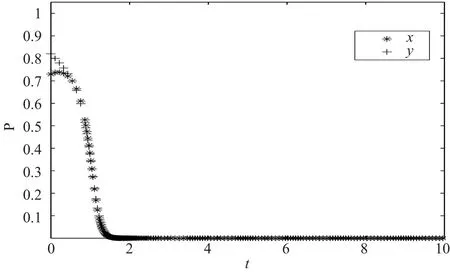
图 11 数值 10 仿真结果Fig.11 The results of simulation group 10
通过上述理论分析与仿真模拟得到以下推论:铁路和地方政府投融资的合作意愿受初始合作意愿的影响,会随二者所占股权份额和所获得的增值收益的增加而增大,随合资铁路公司生产运营管理成本和声誉成本的增加而减小。因此,为促进合资铁路的良性运作与可持续发展,提出以下对策建议。
(1)做好顶层设计,科学合理划分项目类别。政策问题是保障合资铁路公司资产保值增值、提高资产营运效益的根本因素。在国家铁路网规划中,部分铁路项目着重考虑的是国家基础建设、国防等社会因素,经营效益仅属于从属考虑因素。因此,应在对合资铁路项目重新定位的基础上进行顶层设计,并科学、合理地划分类别,并根据划分结果,争取国家相关政策支持和不同程度的财政补贴。
(2)拓宽融资渠道,加大体制机制创新。对于合资铁路建设可以采取多种融资渠道,如争取国家铁路建设专项资金与债券支持、争取商业银行与政策性银行贷款、争取铁路资本金支持、扩大权益性融资渠道、优化收入清算方式、吸引潜在的第三方投资者投资建设等。随着铁路系统改革的不断深入,应通过多元投资、市场运作、统筹规划与政策配套等措施加大铁路投融资体制机制创新。例如,可以利用地方省级投资平台发行合资铁路公司债券;基于铁路混合所有制改革理念,合资铁路公司可以与相应保险资产管理公司合作进行债权投资;结合铁路资产资本化盘活既有铁路股权,实现合资铁路的可持续联动发展;以“土地出让或联合开发”吸引外部社会资本直接投资铁路建设。
(3)完善运营机制,规范合资铁路建设运营模式。结合一些省、直辖市自主建设地方铁路的经验,可以采取工程项目总承包模式,协调多方利益,发挥各自优势,控制好合资铁路建设成本。另外,在机制上,应保障地方投资公司话语权,避免关联交易,并请各方利益主体共同认可的第三方清算机构进行清算,不断完善公司治理模式。总之,由于各地方合资铁路公司股权投资数额较大,但上市资产却极少,结合铁路公司法人治理模式的真正建立,可以考虑推进“资产资本化”,成立股份公司并择时上市,实行资产证券化,以实现合资铁路的可持续发展。
5 结束语
从合资铁路运作管理的现实出发,基于投融资合作视角,借助演化博弈理论与方法,建立铁路和地方政府的演化博弈模型,推导出铁路和地方政府进行投融资合作的相关策略选择。通过博弈研究可以看出:铁路和地方政府通过建立合资铁路公司进而实现双方协同发展的存在基础就是要从有限理性出发,系统与动态地考虑合作双方经济收益与成本支出影响。铁路和地方政府能够有效进行投融资合作进而实现各自的可持续发展,主要依赖于博弈双方初始状态和关键参数的选择。
[1] 祝雪颖. 合资铁路经营亏损原因分析及对策研究[J]. 石家庄铁道大学学报(社会科学版),2017,11(3):37-40.ZHU Xue-ying. Reason Analysis and Countermeasure Research on Operation Loss of Joint Venture Railway[J].Journal of Shijiazhuang Tiedao University(Social Science Edition),2017,11(3):37-40.
[2] 潘晓娟. 合资铁路盈利状况堪忧 铁路投融资改革亟待立法“破冰”[N]. 中国经济导报,2015-01-29(B05).
[3] 许 霞. 铁路投融资改革如何趟过“深水区”[N]. 国际商报,2016-11-17(B04).
[4] 张新玫. 试论地方合资铁路的投融资模式[J]. 新金融,2014(1):17-19.
[5] 徐 微. 铁路企业开展融资租赁业务的探讨[J]. 铁道运输与经济,2018,40(2):24-27.XU Wei. A Study on Raitway Companies Involved in Finance Lease Businesses[J]. Railway Transport and Economy,2018,40(2):24-27.
[6] 祝雪颖. 基于博弈论的合资铁路经营管理体制探讨[J]. 铁道经济研究,2017(3):44-47.ZHU Xue-ying. Discussion on Joint Venture Railway Management System based on Game Theory[J]. Railway Economics Research,2017(3):44-47.
[7] 郭经纬,汤银英,彭其渊. 基于博弈论的铁路融资均衡管理模型研究[J]. 铁道运输与经济,2014,36(8):1-5.GUO Jing-wei,TANG Yin-ying,PENG Qi-yuan. Study on Equilibrium Management Model of Railway Financing based on Game Theory[J]. Railway Transport and Economy,2014,36(8):1-5.
[8] 石云鸣. 推进运输供给侧结构性改革为铁路提质增效开创新思路[J]. 理论学习与探索,2017(3):16-18.

