高速铁路下承式钢桁梁桥结构稳定性分析
吴 鹏,吴运宏,王广程
(1.中铁大桥局 武汉桥梁特种技术有限公司,湖北 武汉 430205;2.桥梁结构健康与安全国家重点实验室,湖北 武汉 430034)
钢桁架具有结构形式简单、重量轻、刚度大、几何特性好、抗压和抗扭性能好、可应用于跨度和载荷都较大的结构等特点,而被广泛运用于铁路桥梁建设中[1-2]。钢桁架梁桥主要承受由桥面传来的竖向和纵向荷载,并将荷载传递给主桁节点,钢桁架任意杆件的破坏都可能导致整体结构破坏[3-4]。钢桁架结构在使用过程中,若变形持续增长,则会导致结构承载力丧失,从而发生失稳破坏[5-8]。因此,为保证桥梁结构安全,对成桥阶段和施工阶段稳定性进行分析意义重大。
1 工程概述
某高速铁路一座下承式钢桁架连续梁桥,跨度组合为(72+90+72)m,见图1。设计速度300 km/h,其主桁高12.0 m,边跨和中跨节间距9.0 m。

图1 钢桁梁桥结构形式(单位:m)
桥面总宽12.5 m,双线线间距4.8 m。桥面系采用密布钢横梁与混凝土桥面板组合形式,并设有2根纵梁,横梁采用1.2 m高工字梁,横梁间距3.0 m。桥面板采用C50混凝土,厚度取0.2 m。
设计荷载包括恒载、活载、摇摆力、制动力、支座沉降和温度荷载。恒载由一期恒载(结构自重)和二期恒载(取150 kN/m)组成,活载采用双线ZK荷载,支座沉降按不均匀沉降10 mm考虑,温度荷载采用系统温差,按±15℃考虑。主桥采用悬臂拼装法施工。
为增加桁架桥横向刚度,分别在桁架桥两端和中间2个支座处设置桥门架,见图2(a),其桥梁结构总体计算模型见图2(b)。

图2 桥门架布置与桥梁结构计算模型
2 成桥阶段稳定性分析
下承式钢桁梁桥主要的稳定验算指标有:整体挠度、整体和局部稳定、杆件长细比。并选取上弦杆A7A8、下弦杆E7E8、斜杆A8E7、竖杆A8E8、上平纵联(中跨支座处)和横梁(中跨跨中节间)等杆件进行验算。
2.1 结构挠度验算
按照桥梁跨度L以及设计速度300 km/h在规范中查阅可知,桥跨由于列车竖向静活载所引起的竖向挠度f应满足验算公式[9-11]
边跨
f≤L/900
(1)
中跨
f≤L/750
(2)
该规定适用于3跨及以上的双线简支梁桥,而本桥为3跨连续梁桥。按照补充规定,3跨连续梁桥竖向挠度限值按上述标准的1.1倍取用。根据MIDAS/Civil的计算结果,结构在竖向静活载作用下的最大挠度为43.1 mm,结构的整体挠度满足要求。
2.2 结构稳定性验算
2.2.1 整体稳定性验算
结构稳定性问题可归纳为两类,第一类为平衡分支问题,即达到临界荷载时,除结构原有平衡状态仍存在外,出现第二个平衡状态。第二类为结构保持一个平衡状态,随着荷载的增加,结构应力较大区域开始出现塑性变形,当荷载达到一定数值后,即使荷载不再增加,结构变形也会持续增长直至破坏,该荷载也称之为临界荷载。虽然在实际工程中第一类失稳是不存在的,但其求解容易,且该解为第二类稳定问题极值点的上限,因此,对第一类稳定问题展开研究意义重大。在一定变形状态下的结构的静力平衡方程式可以写成下列形式
[K]{U}+[KG]{U}={P}
(3)
式中:[K]为结构的弹性刚度矩阵;[KG]为结构的几何刚度矩阵;{U}为结构的整体位移向量;{P}为结构的外力向量。
几何刚度矩阵可表示为荷载系数和受荷载作用的结构的几何刚度矩阵的乘积。
(4)
若结构处于不稳定状态,其平衡方程必须有特殊解,即刚度矩阵的行列式等于0时,发生屈曲(失稳)。
|[Keq]|<0(λ′<λcr):不稳定平衡状态
|[Keq]|=0(λ′=λcr):不稳定状态
|[Keq]|>0(λ′>λcr):稳定状态
因此,式(4)可表述为求解特征值的问题。
(5)

通过特征值分析可求得特征值和特征向量,特征值即为临界荷载,特征向量为对应于临界荷载的屈曲模态。
为验算结构整体稳定性,对成桥模型进行屈曲分析,如图3所示。
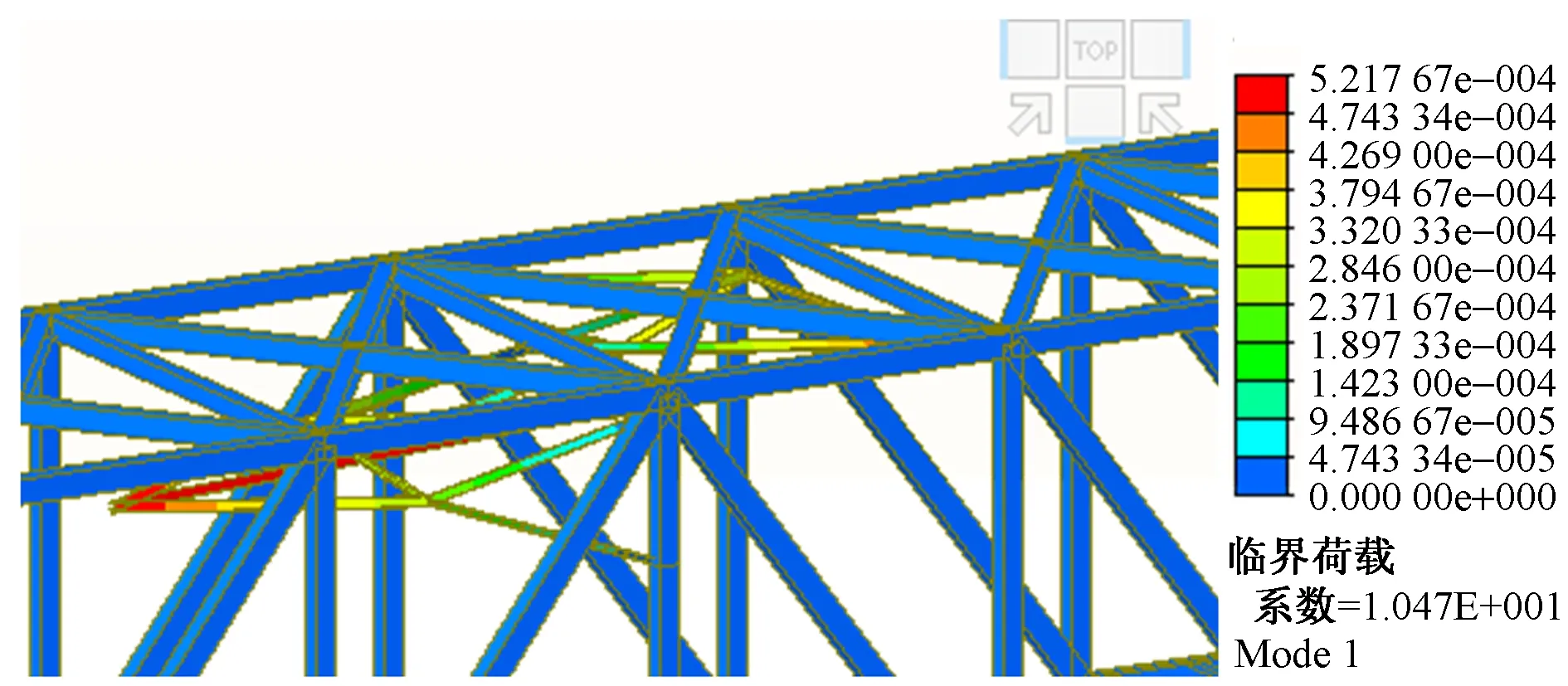
图3 成桥模型屈曲分析
屈曲分析结果表明,结构成桥状态的一阶屈曲模态的荷载系数为10.47,桥梁的整体稳定性良好。其中自重荷载为常量,二期恒载为变量。桥梁结构中桥门架位置易失稳,因此需对桥门架进行加固处理。
2.2.2 杆件稳定性验算
钢桁梁桥杆件常发生压弯破坏[12],根据规范要求,杆件的稳定性按下式进行验算[11]
(6)
由计算结果可知结构在主力和整体降温组合荷载下应力值最大,因此选择该组合下应力情况进行杆件稳定性验算,由表1可知,杆件的稳定性均满足要求。
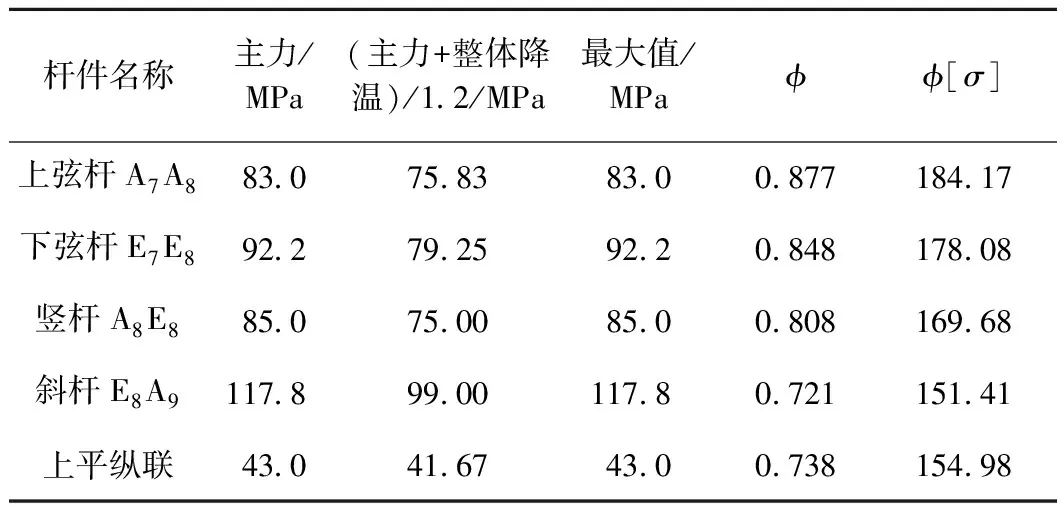
表1 杆件稳定性验算表(表中应力为绝对值)
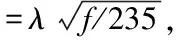
2.3 杆件长细比
杆件长细比验算公式如下
λ=l/r
(7)
(8)
根据铁路桥规规定:主桁杆件的容许长细比[λ]取100[11]。由表2可知,杆件刚度均在容许值范围内,满足要求。

表2 刚度验算表
3 施工阶段稳定性分析
下承式钢桁梁桥常用施工方法主要有悬臂拼装法、膺架法和浮运架设法,本桥使用悬臂拼装法,各施工阶段应力及挠度见表3,其中第4施工阶段(CS4)处于最大悬臂状态,对最大悬臂状态下桥梁结构稳定性进行分析[13]。

表3 悬臂拼装各施工阶段应力及挠度
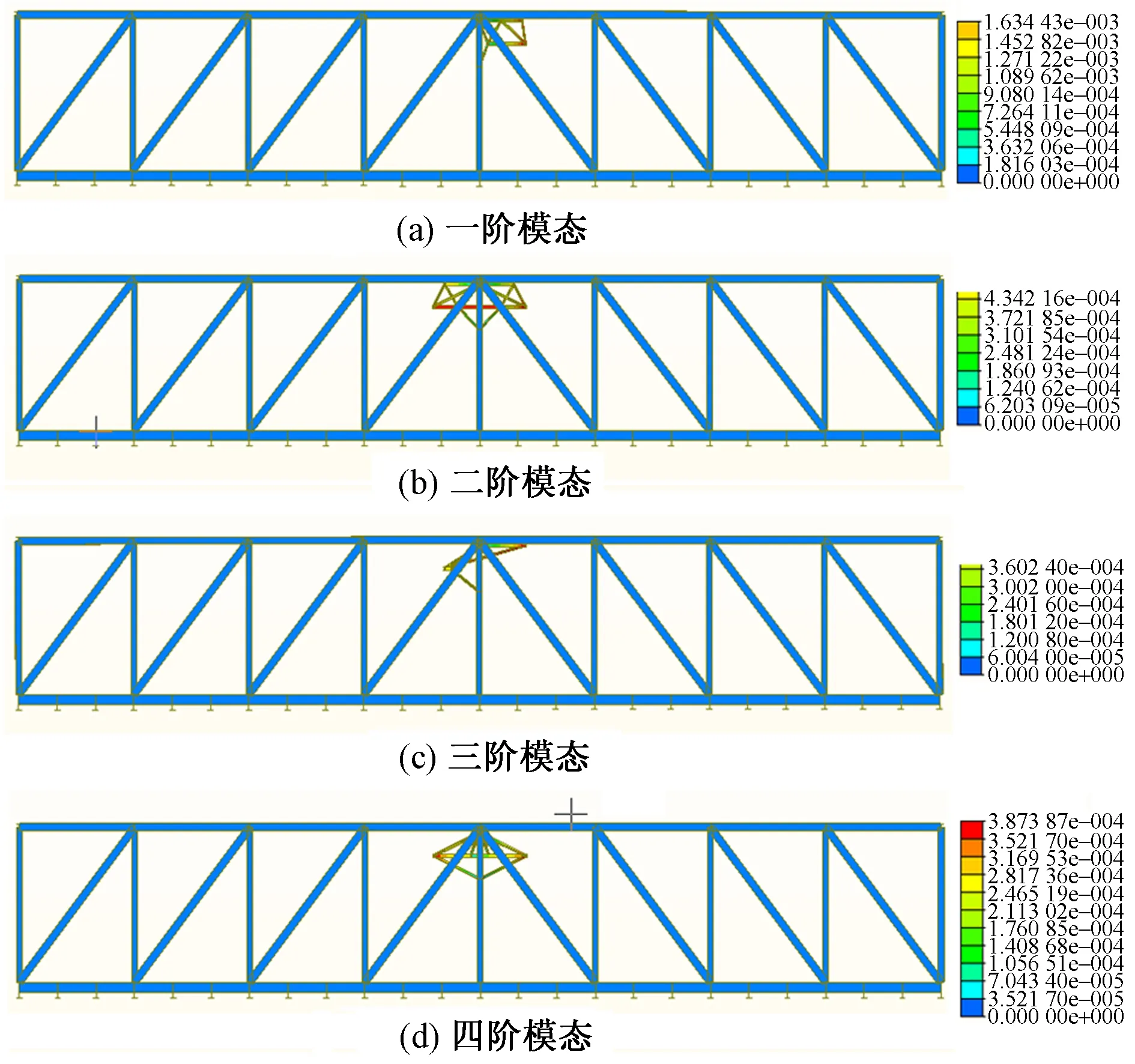
图4 结构各阶模态稳定分析
由图4可知,桥梁结构在最不利施工阶段(CS 4)一阶失稳临界荷载系数为8.177,结构稳定性较高。结构失稳易发生在中间支座处桥门架位置,在施工过程中需要对桥门架进行加固处理,增强桥梁结构的整体稳定性。
4 结论
运用大型有限元软件MIDAS/Civil建立全桥空间有限元模型,对该桥成桥阶段及施工阶段进行稳定性分析后得到以下结论:
1)按照规范要求对钢桁架连续梁桥进行挠度计算,列车竖向静活载和0.5倍升温共同作用下结构产生最大挠度43.1 mm,位于中跨跨中处,满足规范要求。
2)针对成桥阶段结构稳定性和杆件长细比等进行验算,桥梁结构主体及相应杆件均没有发生失稳现象,表明桥梁整体稳定性高。
3)桥梁结构在悬臂拼装各施工阶段应力水平和挠度变形均符合要求,且结构在最不利施工阶段(CS4)仍具有较高的稳定性。但桥门架易发生失稳现象,应对桥门架进行约束加固,提高结构整体稳定性。
[1]王新堂,杨晓明,李俊华.平面预应力钢桁架整体可靠性分析[J].特种结构,2005,22(4):61-64.
[2]刘尚蔚,袁冬卯,仝亮,等.基于Inventor的大型钢架桥三维建模方法[J].华北水利水电大学学报(自然科学版),2013,34(2):71-74.
[3]汪浩,莫雄毅,郑建民,等.某输煤栈桥大跨度桁架吊装技术[J].施工技术,2008,37(7):66-68.
[4]白桦,李宇,李加武,等.钢桁架悬索桥颤振稳定性能研究[J].振动与冲击,2013,32(4):90-95.
[5]苏彦江.钢桥构造与设计[M].成都:西南交通大学出版社,2006.
[6]彭伟.钢结构设计原理[M].成都:西南交通大学出版社,2004.
[7]李亚东.桥梁工程概论[M].成都:西南交通大学出版社,2014.
[8]郭剑.高速铁路下承式结合桥面钢桁梁桥静动力计算分析研究[D].成都:西南交通大学,2009.
[9]中国铁路总公司.TB 10091—2017 铁路桥梁钢结构设计规范[S].北京:中国铁道出版社,2017.
[10]中国铁路总公司.TB 10002—2017 铁路桥涵设计规范[S].北京:中国铁道出版社,2017.
[11]中华人民共和国铁道部.TB 10621—2014 高速铁路设计规范[S].北京:中国铁道出版社,2014.
[12]鞠晓臣,田越,赵欣欣,等.Q500qE高强钢压杆稳定研究[J].铁道建筑,2015,55(10):80-84.
[13]闫志刚.沪通长江大桥专用航道桥双悬臂架设稳定性分析[J].铁道建筑,2017,57(7):24-27.

