基于增量动力分析方法的独塔斜拉桥地震易损性分析

刘陆东，颜全胜，李金武，王孝伟

(1.中国电建集团铁路建设有限公司，北京 100044；2.华南理工大学 土木与交通学院，广东 广州 510640)

近20年来，我国地震灾害频发，造成了许多桥梁结构发生损伤和破坏。斜拉桥等大跨桥梁作为交通枢纽工程，承担着非常重要的交通运输任务，一旦在地震作用下遭到严重破坏，会造成极大的经济损失。斜拉桥具有结构复杂、高柔性等特点，且目前国内外尚无关于大跨斜拉桥的详细抗震设计规范[1]。我国对斜拉桥地震破坏的基础性研究不多，现行桥梁抗震规范对其抗震设计仅给出了基本设计原则。有关斜拉桥抗震性能方面的研究是近年来桥梁抗震研究的热点。

地震易损性分析方法是一种基于概率思想，能在结构抗震分析过程中考虑不确定性因素影响的一种评估方法。该方法从概率的角度对结构的抗震性能进行分析和评估，并已广泛应用于桥梁结构领域中。

对于桥梁结构，通常可按其或其构件在地震作用下损伤状态的不同来确定相应的损伤指标[2]，在此基础上通过地震易损性分析，获得桥梁结构对应不同损伤状态下的超越概率。假设地震作用下结构的地震响应(Response)为R，已定义的损伤指标(Damage Measure)为DM，给定的描述地震作用强度的地震动强度参数(Intensity Measure)为IM，则结构在给定地震动强度的地震作用下发生超过某个损伤指标的损伤超越概率Pf为[3]

Pf=P[R≥DM|IM]

(1)

根据求得的损伤超越概率可进一步建立相应的地震易损性曲线，进而从宏观角度上对桥梁结构的抗震性能进行评估。

本文以一座混凝土独塔斜拉桥为工程背景，基于增量动力分析方法(Incremental Dymamic Analysis,IDA)对该桥进行地震易损性分析。建立了4种损伤状态下桥梁主要易损构件的地震易损性曲线以及结构整体易损性曲线，为同类桥梁的抗震设计以及地震风险评估提供参考。

1 基于IDA的地震易损性分析方法

IDA方法是一种用于结构的地震易损性分析的常用方法，主要利用有限元模拟计算结果与理论分析结果构建桥梁结构的地震易损性曲线。目前该方法在桥梁领域中应用得较为成熟和广泛[3-4]，通过IDA方法进行地震易损性分析的主要步骤如下：

1)选取一定数量的地震波并确定合适的地震动强度参数IM；

2)将选好的地震波“标准化”，根据IM进行缩放，得到多组不同强度水平的地震波；

3)将缩放后得到的地震波输入到桥梁动力弹塑性分析模型中，进行非线性时程分析，并提取桥梁各构件地震响应的最大值；

4)确定损伤指标，整理时程分析结果。得到用以描述桥梁构件损伤状态的工程需求参数(EDP)的结果数据样本，并通过回归分析确定易损性函数。在分析过程中，假定通过时程分析得到的EDP与IM满足指数函数关系[5-6]

EDP=a(IM)b或ln(EDP)=lna+bln(IM)

(2)

式中a和b均为常数,可通过最小二乘法对时程分析结果数据进行拟合得到。

相应的标准差ξ采用下式表示，其中n为输入桥梁分析模型的地震波数量。

(3)

进一步假定EDP满足正态分布，则损伤超越概率Pf可用标准正态分布函数Φ表示为

(4)

5)根据已建立的易损性函数形成桥梁构件的地震易损性曲线，进而获得桥梁整体易损性曲线。

2 工程背景与分析模型

2.1 工程背景

本文的研究对象为一座位于某地级市市区内的混凝土独塔斜拉桥。该桥结构体系为塔墩梁固结体系，所处场地抗震设防烈度为8度。桥梁边跨设有一辅助墩，边墩和辅助墩的墩顶均设置铅芯橡胶支座，跨径布置分别为180,100,50 m。桥梁主梁采用C60混凝土，标准截面梁高为3.0 m，桥面宽度为30.5 m。桥梁主塔采用C50混凝土，由4个独立塔柱、横向联系梁、纵向联系梁组成，塔高105 m，斜拉索呈平面双索面扇形布置，全桥斜拉索共有88根。斜拉桥布置如图1所示。

图1 斜拉桥布置(单位：cm)

2.2 有限元分析模型

本文算例斜拉桥的非线性动力有限元模型是基于OpenSees软件建立的。在分析模型中，桥梁主跨边墩、边跨边墩及辅助墩、主塔1#索锚固区位置以下的塔柱及横梁均采用弹塑性纤维单元(Nonlinear Beam Column Element)来模拟，纤维模型中的混凝土和钢筋材料分别采用Concrete 04和Steel 01材料来定义。桥梁主塔1#索锚固区位置以上的塔柱及横梁和斜拉桥的主梁均用弹性梁单元(Elastic Beam Column Element)来模拟。桥梁支座用0长度单元(Zero Length Element)来模拟。斜拉索则采用桁架单元(Truss Element)模拟，斜拉索索力以初应变的形式施加，且斜拉索与主梁、主塔之间采用刚臂单元连接。墩底及4个主塔塔柱底部的边界条件在模型中均简化为固结。

3 桥梁地震易损性分析

3.1 地震动的选取

当选取的地震波具有代表性时，地震易损性分析结果能够较好地反映结构在各地震波作用下的随机性[7]。本文研究桥梁所处场地类别为Ⅲ类，场地土类型是中软土。根据桥梁场地类型条件，将抗震设计规范规定的E2反应谱设为目标谱，从美国太平洋地震工程研究中心(PEER)强震数据库中选取地震波。选波时设定相应的剪切波速范围，所选地震波断层距均>30 km，地震波震级均在6.0～7.0，最终从数据库中选取了16条天然地震波。所选地震波反应谱曲线及规范目标反应谱曲线对比见图2。以地震波峰值加速度(PGA)为地震动强度参数，将已选取的16条地震波的PGA标准化到0～0.8g，每级为0.05g，生成用于地震易损性分析的256条地震波。本文输入到模型中的地震波均沿纵桥向输入。

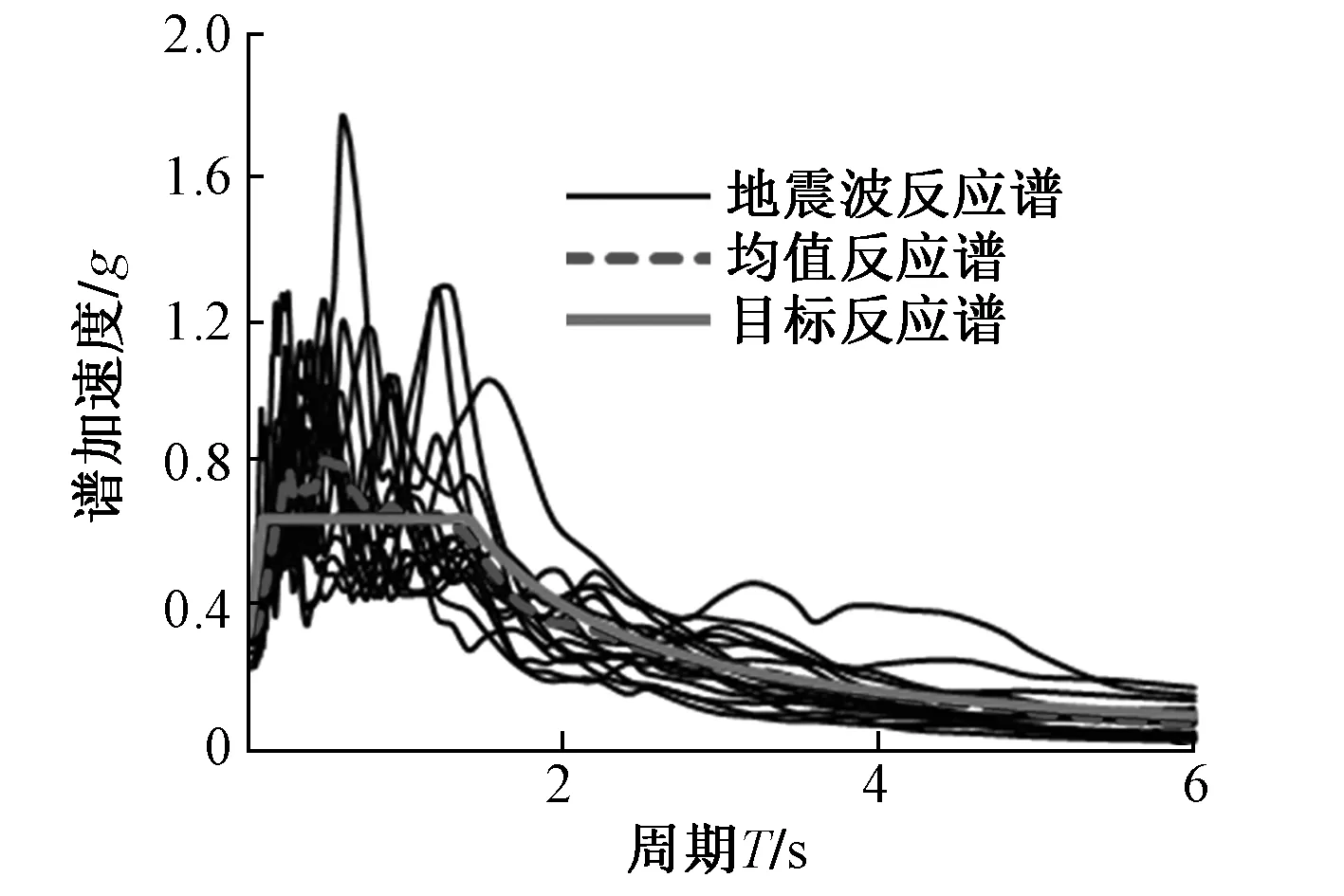
图2 地震波加速度反应谱曲线

3.2 损伤指标的确定

对于桥梁结构，通常可将其在地震作用下的损伤程度分为轻微损伤、中等损伤、严重损伤、完全损伤4个等级[3]。本文所研究桥梁为固结体系斜拉桥，在地震作用下桥梁的易损部位包括主塔塔底、主塔塔梁交界处、桥墩墩底、桥梁支座等位置，且斜拉桥的主塔、桥墩及支座等构件的损伤程度对桥梁整体抗震性能有较大影响[8-9]，故本文主要针对斜拉桥主塔、桥墩、支座构件对算例斜拉桥进行地震易损性分析。

对于主塔和桥墩，依据CHOI等[10]的研究结果，本文采用曲率延性系数定义桥墩及主塔的损伤指标。通过XTRACT软件建立塔底截面、主塔塔梁交界处截面及边墩和辅助墩墩底截面的纤维截面模型并输出各截面的首次屈服曲率，将曲率延性系数定为地震作用下桥梁构件截面曲率与截面首次屈服曲率两者的比值，并将4种损伤状态下对应的截面曲率延性系数取为1,2,4,7。由于算例斜拉桥主塔有4根塔柱，在提取塔底截面以及主塔塔梁交界处截面的曲率延性系数计算结果时，取各截面中损伤概率最大者建立主塔易损性曲线。

剪切破坏一直是支座破坏的一种主要形式，依据李立峰等[11]的研究成果，本文以支座位移延性比来定义桥梁各铅芯橡胶支座的损伤指标，并取4种损伤状态下对应的支座位移延性比为1.0,1.5,2.0,2.5。其中，支座位移延性比为1.0时对应的支座剪切应变为100%，橡胶支座容许剪切应变γa的计算公式为

(5)

式中:umax为地震作用下支座最大位移响应;t为橡胶层总厚度。

3.3 地震易损性曲线的建立

3.3.1 构件易损性曲线

将生成好的256条地震波沿纵桥向输入到桥梁OpenSees模型中，进行IDA分析，建立桥墩、主塔以及支座的地震易损性曲线，结果见图3—图5。

图3 桥墩地震易损性曲线

图4 主塔地震易损性曲线

由图3可知，桥墩易损程度从高到低依次为辅助墩、主跨边墩和边跨边墩，对应轻微损伤和中等损伤这2种损伤状态各墩易损性曲线非常相近。

由图4可知，桥梁主塔较易发生轻微损伤和中等损伤。相比之下，发生严重损伤和完全损伤的超越概率明显较小，但仍存在发生严重损伤和完全损伤的可能性。

由图5可知，支座易损程度从高到低依次为边跨边墩支座、辅助墩支座和主跨边墩支座。

图5 支座地震易损性曲线

对比图3、图4和图5可知，斜拉桥各构件的地震易损性均随PGA增大而增大。相比其他构件，在地震波纵向激励下，辅助墩、主跨边墩以及边跨边墩处支座发生损伤的超越概率相对较高。

3.3.2 整体易损性曲线

桥梁是由多个不同构件构成的整体结构，在地震作用下，当桥梁某个构件或多个构件同时进入损伤状态时，桥梁整体抗震性能也会受到影响[12-13]。因此，在对斜拉桥构件进行地震易损性分析的基础上，本文通过基于可靠度理论的一阶界限法进一步对桥梁进行了整体易损性分析，得到了桥梁在各级损伤状态下超越概率的上下界限。

假设桥梁整体结构体系为易损构件组成的串联体系，在该体系中，任一构件失效时整个结构都将会失效，则对应的结构整体失效概率的边界为

(6)

式中：Pi为单个构件的失效概率；Pf为结构整体的失效概率;m为构件数量。

失效概率的下界对应结构中各构件最大失效概率,失效概率的上界则对应各构件失效事件不同时发生的情况下结构整体的最大失效概率。

通过式(1)—式(4)可得各构件对应各级损伤状态的超越概率，将其代入式(6)中即可得到桥梁整体在各级损伤状态下超越概率的上下界，进而形成整体地震易损性曲线，见图6。

图6 桥梁整体地震易损性曲线

由图6可知，算例斜拉桥发生轻微损伤和中等损伤的超越概率较高。对比图3—图6可以发现，桥梁整体在各级损伤状态下的超越概率明显大于各构件的损伤超越概率。

4 结论

本文通过OpenSees程序建立了一座混凝土独塔斜拉桥的动力弹塑性分析模型并进行了非线性时程分析。采用IDA法建立了桥梁桥墩、主塔及支座的纵桥向地震易损性曲线。基于可靠度理论，采用一阶界限法进一步对桥梁进行了整体易损性分析。主要结论如下：

1)斜拉桥桥墩、主塔及支座的地震易损性均随PGA的增大而增大。在纵桥向地震作用下，斜拉桥主塔易发生轻微损伤和中等损伤；斜拉桥桥墩易损性程度由大到小依次为辅助墩、主跨边墩、边跨边墩；斜拉桥支座易损性程度由大到小依次为边跨边墩支座、辅助墩支座、主跨边墩支座。

2)与其他构件相比，斜拉桥辅助墩、主跨边墩以及边跨边墩处支座发生各级损伤的超越概率相对较高，在进行桥梁设计时应予以重视，必要时需考虑对这些构件的抗震设计进行优化。

3)斜拉桥整体较易发生轻微损伤和中等损伤,斜拉桥整体的易损性要大于任何单一构件，仅采用构件地震易损性来表征桥梁整体的地震易损性会给桥梁整体抗震性能评估带来一定误差。

[1]夏修身，李建中，管仲国，等.斜拉桥桥塔非线性抗震性能研究[J].中国公路学报，2016，29(3):66-72.

[2]庞于涛，袁万城，沈国煜，等.基于结构易损性分析的公路桥梁可靠度研究[J].哈尔滨工程大学学报，2012(9)：1091-1096.

[3]冯杰.桥梁结构地震易损性分析研究[D].成都：西南交通大学，2010.

[4]张菊辉，基于数值模拟的规则梁桥墩柱的地震易损性分析[D].上海：同济大学，2006.

[5]ZHANG J,HUO Y.Evaluating Effectiveness and Optimum Design of Isolation Devices for Highway Bridges Using the Fragility Function Method[J].Engineering Structures,2009,31(8):1648-1660.

[6]王晓伟，叶爱君，沈星，等.大跨度桥梁边墩横向减震体系的地震易损性分析[J].同济大学学报(自然科学版)，2016，44(3)：333-340.

[7]黄佳梅.基于IDA的高墩大跨桥梁抗震性能研究[D].长沙：湖南大学，2012.

[8]冯清海.特大桥梁地震易损性与风险概率分析[D].上海：同济大学，2008.

[9]焦驰宇.基于性能的大跨斜拉桥地震易损性分析[D].上海：同济大学，2008.

[10]CHOI E,DESROCHES R,NIELSON B.Seismic Fragility of Typical Bridges in Moderate Seismic Zones[J].Engineering Structures,2004,26(2)：187-199.

[11]李立峰，吴文朋，黄佳梅，等.板式橡胶支座地震易损性分析[J].湖南大学学报(自然科学版)，2011，38(11)：1-6.

[12]宋帅,钱永久,吴刚.桥梁系统地震易损性分析的混合Copula 函数方法[J].工程力学,2017,34(1)：219-227.

[13]郑凯锋，陈力波，庄卫林，等.基于概率性地震需求模型的桥梁易损性分析[J].工程力学，2013，30(5)：165-171.