碰撞参数对隔震桥梁地震响应的影响

彭刚辉，郑史雄，贾宏宇

(1.成都理工大学 工程技术学院，四川 乐山 614000 ；2.西南交通大学 土木工程学院，四川 成都 610031)

地震作用下，梁体在伸缩缝处的碰撞现象十分普遍。2008年发生的汶川地震中诸多桥梁在相邻梁体之间的伸缩缝处发生碰撞[1]。1995年日本Hanshin高速公路桥梁在Kobe地震中因发生较大的位移导致桥梁梁体在伸缩缝处发生了碰撞[2]。梁体间的碰撞会对桥梁结构地震响应产生一定的不利影响。王军文等[3-4]研究表明桥梁伸缩缝处的碰撞效应对结构的地震反应有较大的影响，具体表现在桥梁结构的整体动力响应被加大，过大的纵向振动导致结构的内力、位移等增大。对于位于高烈度山区的桥梁，因其地质构造复杂，地震作用强烈，梁体间的相互碰撞引起结构的地震响应更加复杂。采用隔震设计可延长结构周期并减小地震作用下结构的地震反应[5-6]，但梁的位移响应会增大[7]。在伸缩缝宽度相同时，与非隔震桥梁相比，隔震桥梁更容易发生碰撞[8]，导致结构动力响应增大，故更应引起重视。本文以某高烈度山区隔震桥梁为例，基于碰撞原理，从碰撞参数对隔震桥梁地震响应产生的影响出发，主要探讨了碰撞刚度、伸缩缝间隙和恢复系数3个要素对桥梁地震响应的影响。

1 碰撞原理及要素

对于预应力混凝土隔震连续梁桥，上部结构纵向刚度一般较大，可将其视为刚体[9]。在梁体发生碰撞时，由于碰撞持时较短，梁体间的碰撞过程可以等效为图1的碰撞模型[10]。

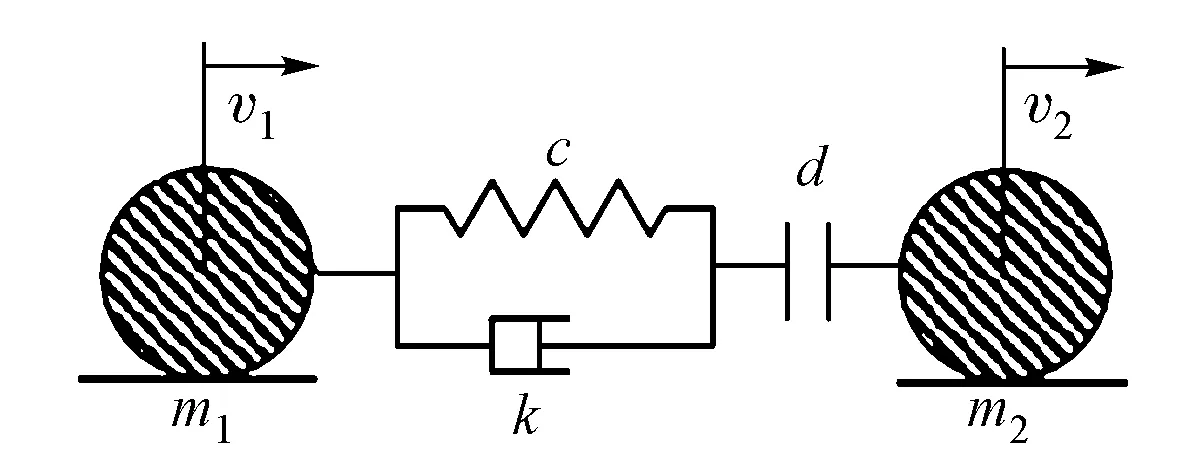
图1 碰撞模型

对于碰撞，当前普遍采用的模拟方法为接触单元法，即在伸缩缝处布置碰撞单元，当梁体同向相对位移差大于伸缩缝间隙时即发生碰撞。碰撞单元中的弹簧用来模拟撞击力，阻尼器用来模拟碰撞过程中的能量耗散。撞击力F计算公式为

(1)

式中:k为连接弹簧的刚度;c为阻尼系数;v为邻梁相对速度;d为结构伸缩缝间隙;d0为结构相对位移差绝对值。

根据碰撞过程中的动量守恒定律及能量守恒定律，阻尼系数为[11]

(2)

(3)

式中:ξ为振型阻尼比；m1,m2分别表示碰撞两物体质量;r为碰撞过程中的恢复系数，取值范围为0～1。

从以上可见，在地震作用下影响梁体碰撞的主要要素为碰撞刚度、伸缩缝间隙、恢复系数、相对速度等，前3个要素对碰撞的影响更加直接且更有研究意义，故而本文主要研究碰撞刚度、伸缩缝间隙和恢复系数对隔震桥梁地震响应产生的影响。

2 桥梁结构模型及地震动输入

采用四川省汶川县境内某2联3×40 m的隔震连续梁桥为算例。该桥主梁由10片T形梁(C50混凝土)组成，单跨总质量为837 t，1#～5#桥墩墩身高度分别为9,16,27,21,12 m。3#墩处设伸缩缝，梁体间的碰撞发生在此处。桥梁立面如图2所示。

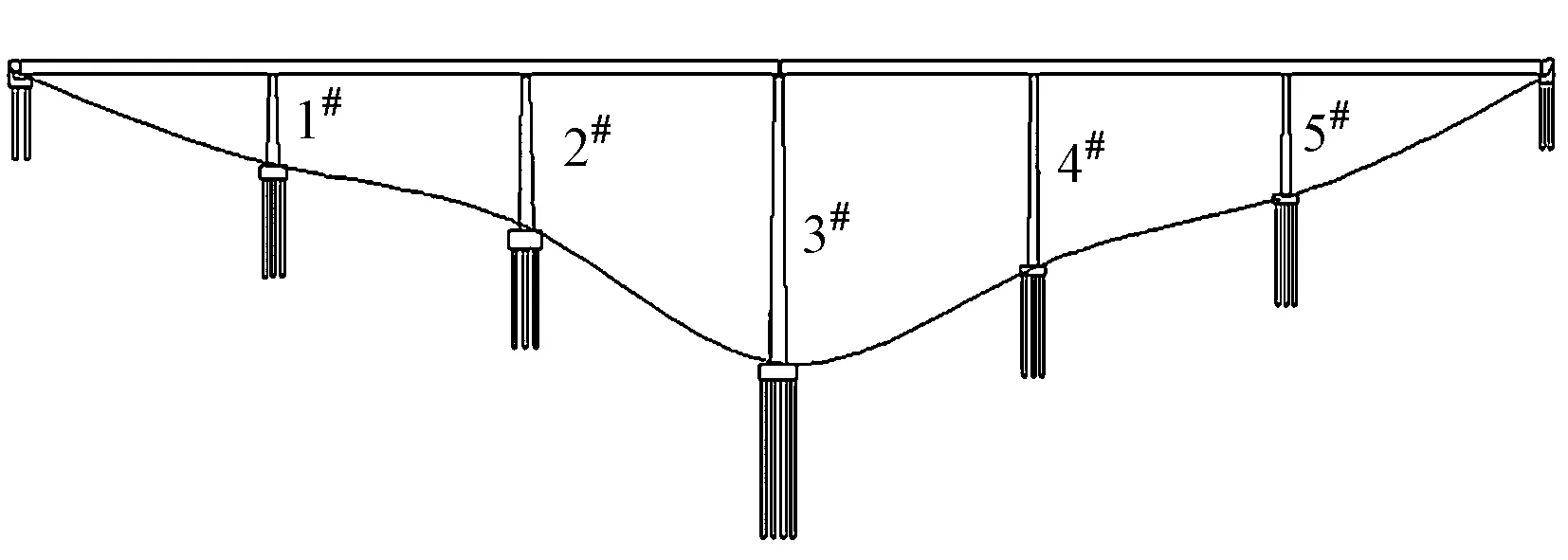
图2 桥梁立面

利用ANSYS建立全桥模型并进行数值模拟分析。梁体间的碰撞采用接触单元Combin 40进行模拟，该单元可模拟碰撞刚度、伸缩缝间隙和恢复系数。Combin 40单元中初始碰撞刚度取梁体间的轴向刚度，恢复系数取0.65[8,12]，伸缩缝初始间隙取0.04 m。桥梁支座采用铅芯橡胶隔震支座，其计算参数根据JT/T 822—2011《公路桥梁铅芯隔震橡胶支座》选取[13]，其铅芯屈服力为142 kN，剪切弹性模量0.8 MPa，屈服前水平刚度为7.1 kN/mm，容许水平位移为±100 mm，则支座所能承受的最大水平剪力为7.1×100=710 kN。

为使计算结果更具可靠性，地震动数据选择5条具有代表性的天然地震波，如表1所示。采用非线性动力时程法进行地震时程分析，阻尼模型采用Rayleigh阻尼，其质量和刚度因子根据阻尼比(取0.05)与结构周期采用Rayleigh阻尼公式计算求得，地震动考虑顺桥向的一致激励作用，且只考虑2联连续梁体间的碰撞，不考虑梁体与桥台间的碰撞。

表1 选取的地震波

3 地震响应分析

强烈地震作用对隔震支座产生的破坏较严重，尤其是对桥墩的破坏最为明显，因此本文主要以桥墩(3#墩)及隔震支座为分析对象。因墩顶位移可反映墩底弯矩及剪力的实际情况，故桥墩的地震响应主要以墩顶位移为分析对象，而对隔震支座主要分析其水平剪力，重点研究碰撞刚度、伸缩缝间隙和恢复系数对墩顶位移、梁体间的碰撞力及支座水平剪力的影响。

3.1 梁体碰撞对隔震桥梁结构地震响应的影响

梁体间碰撞对桥梁地震响应的影响如图3所示。可知，在地震作用下，只有当梁体间相对位移超过了初始间隙时才发生碰撞，且梁体间的碰撞作用使桥墩底部的弯矩减小，即碰撞作用有利于减小墩底弯矩。梁体间的碰撞使支座滞回特性发生了改变，使其支座水平剪力增加，而支座剪切变形则相对减小，说明梁体间的碰撞对隔震支座会产生一定影响。

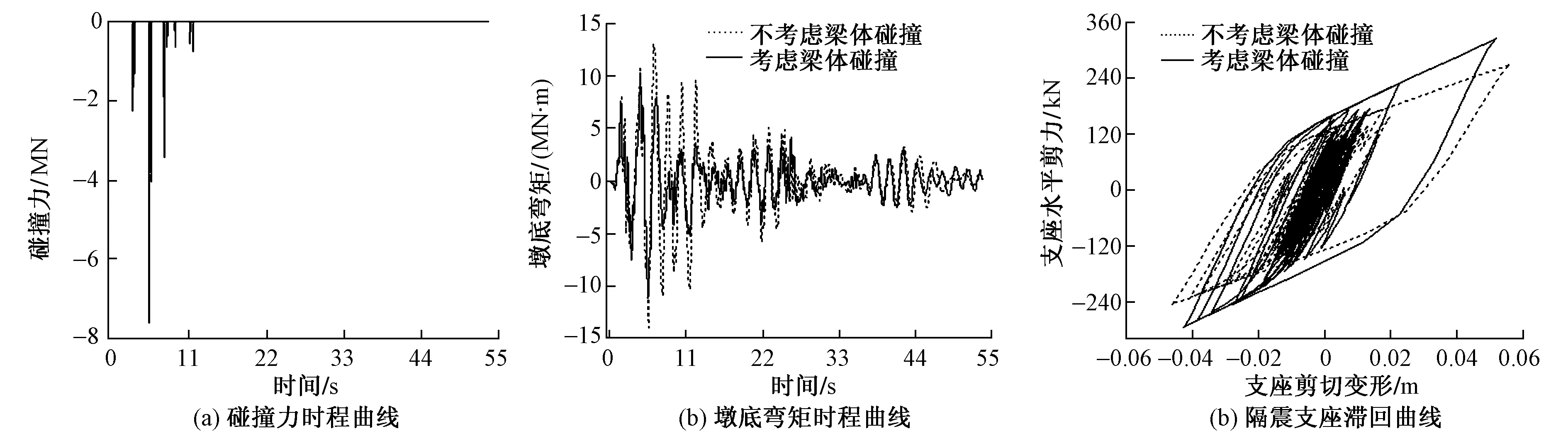
图3 梁体碰撞对桥梁结构地震响应的影响

3.2 碰撞刚度对隔震桥梁地震响应的影响

碰撞刚度取值的不同，对桥梁结构产生的地震响应也会有所不同。故根据参考文献[10,14-15]，桥梁碰撞反应分析的碰撞刚度k的取值范围设置为105～106kN/m，以研究地震作用下碰撞刚度对桥梁结构地震响应的影响。伸缩缝间隙取0.04 m，以保证梁体间能发生碰撞，恢复系数取0.65。地震作用下碰撞刚度对桥梁地震响应产生的影响见图4。可知，在5条地震波作用下，最大碰撞力随碰撞刚度的增大而增大，最大增幅255%，最小增幅220.1%，平均增幅241.2%。墩顶位移峰值随碰撞刚度的增大而增大，最大增幅96.9%，最小增幅67.3%，平均增幅80.2%，从而亦可得出碰撞刚度的增大会导致墩底弯矩及剪力的增大。隔震支座水平剪力峰值最大增幅64.9%，最小增幅56.7%，平均增幅60.3%。由此说明碰撞刚度对梁体间碰撞力、墩顶位移以及隔震支座均会产生影响，尤其是对梁体间的碰撞力影响最明显，且不同的碰撞刚度对结构地震响应产生的影响也不相同。

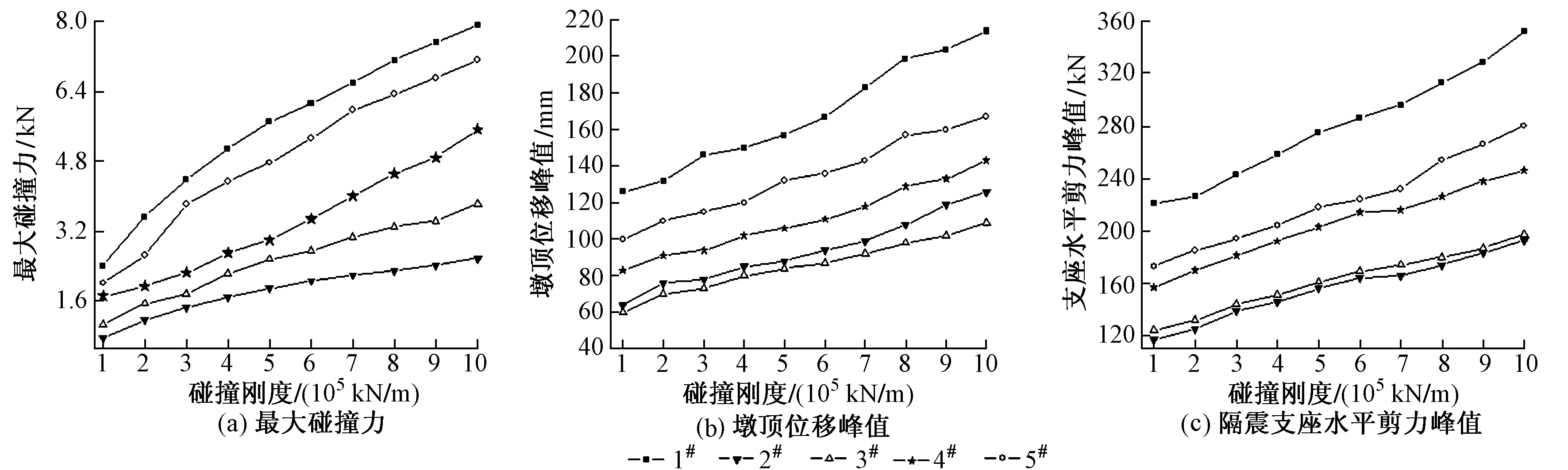
图4 地震作用下碰撞刚度对结构地震响应的影响

3.3 伸缩缝间隙对隔震桥梁地震响应的影响

研究伸缩缝间隙对桥梁结构地震响应的影响时间隙值取1～10 cm，碰撞刚度取梁体轴向刚度，恢复系数取0.65[12]。

地震作用下伸缩缝间隙对桥梁地震响应的影响见图5。可知：最大碰撞力随间隙的增大先增大后减小，最后减小为0。墩顶位移峰值及隔震支座水平剪力峰值随间隙的增大先减小后变大，然后保持恒定。当碰撞力随着间隙的增大而增大时，墩顶位移及支座水平剪力在减小，反之亦然；当梁体间不再发生碰撞(碰撞力为0)时，墩顶位移及支座水平剪力恒定不变。由此说明：梁体间的最大碰撞力、墩顶位移峰值和隔震支座水平剪力峰值都与伸缩缝间隙有关，间隙小，碰撞力较小，墩顶位移及隔震支座水平剪力较大；间隙大，碰撞力很小，墩顶位移及隔震支座水平剪力较大，即随着间隙的增加，墩顶位移及隔震支座水平剪力与碰撞力的变化规律相反。当间隙为3～5 cm 时墩顶位移及隔震支座水平剪力较小，但碰撞力较大。因此，合理的伸缩缝间隙有利于减小隔震支座水平剪力，同时也会使墩顶位移减小，进而减小墩底弯矩及剪力，可起到保护桥墩的作用，但应注意碰撞力偏大引起的落梁等破坏。

图5 地震作用下伸缩缝间隙对结构地震响应的影响

3.4 恢复系数对隔震桥梁地震响应的影响

碰撞过程中的能量损失采用阻尼表示，阻尼的大小与碰撞过程中的恢复系数有关。对于完全弹性碰撞，恢复系数r=1.0；完全塑性碰撞，恢复系数r=0。实际上的梁体碰撞既不是完全弹性碰撞，也不是完全塑性碰撞，而是介于两者之间，故而将恢复系数设置为0.1～0.9。碰撞刚度取梁体轴向刚度，伸缩缝间隙取0.04 m[10,12]，以研究地震作用下恢复系数对隔震桥梁地震响应的影响。

地震作用下恢复系数对桥梁地震响应的影响见图6。可知：5条地震波作用下各地震响应规律基本一致，最大碰撞力随恢复系数的增大而减小，最大减幅为31.9%，最小减幅为9.6%，平均减幅21%。墩顶位移峰值随恢复系数的增大而增大，最大增幅21.4%，最小增幅12.6%，平均增幅19.1%。隔震支座水平剪力峰值随恢复系数的增大而增大，最大增幅41.8%，最小增幅28.7%，平均增幅35.9%。由此可见：恢复系数越大，墩顶位移及支座水平剪力越大，而梁体间的碰撞力越小，这与碰撞原理及阻尼耗能有关，根据式(1)—式(3)，恢复系数越大，阻尼比越小，在碰撞刚度及伸缩缝间隙不变时，阻尼越小，梁体间的碰撞力也越小。同时，系统的耗能能力也将变弱，作用在桥梁结构上的地震能量则相应增加，故墩顶位移及支座水平剪力变大。

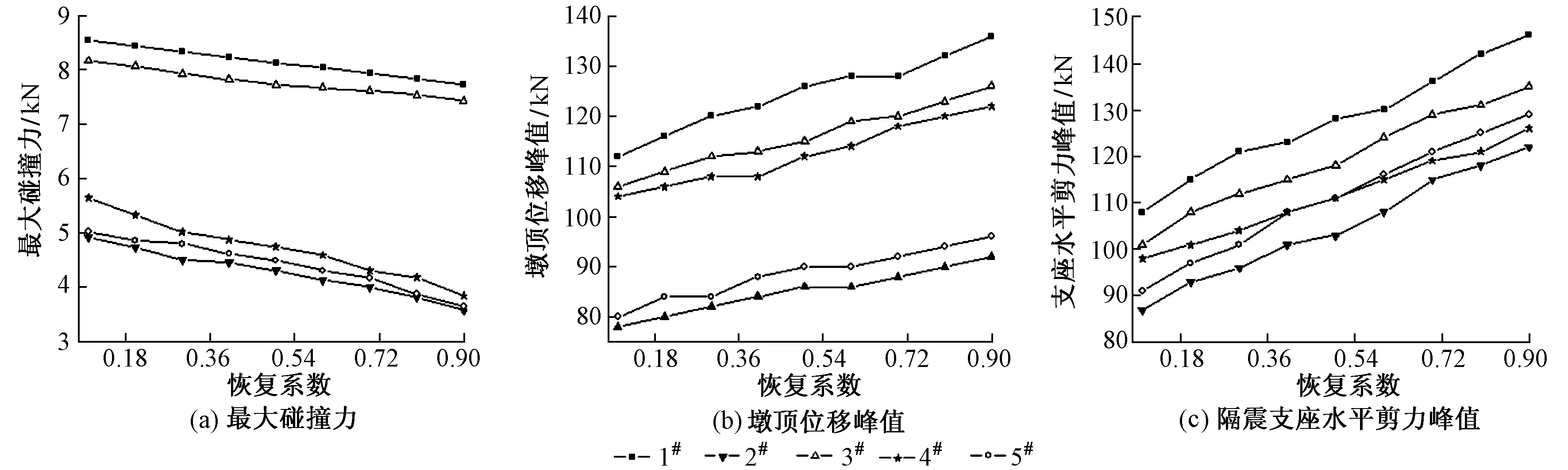
图6 地震作用下恢复系数对结构地震响应的影响

4 结论

本文以一座隔震连续梁桥为例，利用非线性时程法研究了碰撞组成要素(碰撞刚度、伸缩缝间隙和恢复系数)对桥梁结构地震响应的影响。通过分析得出以下结论：

1)在地震作用下，碰撞力、墩顶位移以及隔震支座水平剪力随碰撞刚度的增大而增大。其中，碰撞力的增幅最大。

2)梁体伸缩缝间隙直接影响梁体间的碰撞力、墩顶位移和隔震支座水平剪力。随着间隙的增加，墩顶位移和隔震支座水平剪力与碰撞力的变化规律相反。当间隙为3～5 cm时，墩顶位移及隔震支座水平剪力较小,但碰撞力较大。因此，合理的伸缩缝间隙有利于减小隔震支座水平剪力及墩顶位移，进而减小地震对桥墩产生的作用，但此时应注意碰撞力偏大导致的落梁等破坏。

3)碰撞阻尼模型当中的恢复系数越大，墩顶位移及支座水平剪力越大，而梁体间的碰撞力越小。

[1]李乔，赵世春.汶川大地震工程震害分析[M].成都：西南交通大学出版社，2008.

[2]Earthquake Engineering Research Institute(EERI).The Hyogo-ken Nanbu Earthquake of January 17,1995-preliminary Reconnaissance Report[R].Oakland,CA：EERI,1995.

[3]王军文，李建中，范立础.非规则梁桥伸缩缝处的碰撞对地震反应的影响[J].土木工程学报，2006，39(1):54-59.

[4]李建中，范立础.非规则梁桥纵向地震反应及碰撞效应[J].土木工程学报，2005，38(1):84-90.

[5]李一鸣,虞庐松,南鹏.高烈度地震区曲线连续梁桥的减隔震方案研究[J].铁道建筑,2017,57(9):43-47.

[6]邱新林,廖平,赵人达,等.多跨连续梁桥的隔震方案研究[J].铁道建筑,2017，57(6):41-43.

[7]左志鹏，王义强.减隔震技术在连续梁桥中的应用[J].防灾减灾工程学报,2013,33(增):154-160.

[8]李黎，叶志雄，吴璟.隔震连续梁桥地震作用下梁间碰撞响应的研究[J].公路交通科技,2009,26(7):100-104.

[9]邓育林，彭天波，李建中.地震作用下桥梁结构横向碰撞模型及参数分析[J].振动与冲击，2007，26(9)：104-107.

[10]李忠献，岳福青，周莉.地震时桥梁碰撞分析的等效Kelvin撞击模型[J].工程力学，2008，25(4):128-133.

[11]ANAGNOSTOPOULOS S A.Equivalent Viscous Damping for Modeling Inelastic Impacts in Earthquake Pounding Problems[J].Earthquake Engineering & Structural Dynamics,2004,33(8):897-902.

[12]JANKOWSKI R,WILDE K,FUJINO Y.Reduction of Pounding Effects in Elevated Bridges During Earthquakes[J].Earthquake Engineering & Structural Dynamics,2015,29(2):195-212.

[13]中华人民共和国交通运输部.JT/T 822—2011 公路桥梁铅芯隔震橡胶支座[S].北京:人民交通出版社，2012.

[14]王东升,王国新,冯启民.桥梁结构地震反应邻梁碰撞分析等效刚体模型[J].工程力学，2004,21(4):81-85.

[15]DESROCHES R,MUTHUKUMAR S.Implications of Seismic Pounding on the Longitudinal Response of Multi-span Bridges-an Analytical Perspective[J].Earthauake Engineering and Engineering Vibration,2004,3(1):57-65.