结合IGS分析中心产品的轨道综合算法及其精度分析

陆轶材，高成发，郭 奇

(东南大学交通学院，江苏 南京 210096)

IGS轨道和钟差产品是精密定位等重要的基础数据，也是维持卫星导航系统时空基准的重要产品。目前IGS运行的数据处理分析中心不少于12家，主要包括欧洲定轨中心(CODE)、加拿大自然资源部(EMR)、欧洲空间局(ESA)、德国波兹坦地学研究中心(GFZ)、法国空间研究中心(GRG)、美国喷气动力实验室(JPL)、美国麻省理工学院(MIT)、美国国家大地测量局(NGS)、美国斯克里普斯海洋学研究所(SIO)、美国海军天文台(USN)、捷克大地实验室(GOP)和武汉大学(WHU)均能独立解算，生成精度优于5 cm的GNSS精密轨道[1-3]。由于各家分析中心使用的基准站坐标、数据处理软件及定轨策略等不尽相同，定轨结果会存在明显的差异[4]。IGS对多个分析中心产品进行质量分析，然后通过综合解算生成参考框架和时间基准稳定、统一且1 d精度优于2.5 cm的综合产品[5-7]。

随着IGS分析中心的发展，IGS产品综合的方法不断得到改进和完善。文献[4]表明分析中心的轨道坐标存在系统偏差，且该偏差与极移参数之差相关；文献[8]提出了一种利用L1G范数法求取转换参数进行轨道产品加权平均的综合算法。文献[9—11]探讨和分析了IGS产品的一致性问题，提出利用旋转变换和附加改正等方法维持IGS最终轨道/钟差和周解SINEX等产品的一致性。文献[12]总结了IGS轨道产品综合的3种常用的加权平均定权方法：等权法、基于Helmert转换的验后方差定权法及方差因子定权法。文献[13]通过选择最优的分析中心组合和框架差异消除方法进行精密轨道综合，极大提升了合成轨道的精度。现有文献中常用的定权方法均是以各分析中心等权平均轨道为参考轨道，进行参数估计，很少基于分析中心框架、轨道RMS趋于稳定的方向对轨道综合的研究。IGS最终轨道产品在每周四发布且具有12～18 d的时延性，相比之下分析中心的轨道产品则提前2～3 d，即IGS的最终综合产品通常需要在分析中心产品全部提交后的2～3 d后才能得到，因此对分析中心的轨道产品进行综合生成精度更优的产品是极具工程意义的。故本文提出了基于IGS分析中心产品的轨道综合算法，并自行编写程序对GPS卫星轨道进行综合，为北斗系统中不同类型卫星(如GEO/IGSO/MEO)轨道综合方法提供参考，为iGMAS中心的建设提供建议[14-16]。

1 轨道综合原理及数学模型

目前IGS仅发布GPS、GLONASS综合轨道产品，产品综合方法有两种：动力学法和加权平均法。第一种方法是将各分析中心产品作为伪观测数据进行轨道确定，估计卫星初始状态和其他动力模型参数，保持了轨道动力学特性，可靠性较高，但增加了算法复杂度，且轨道和钟差综合无法采用同一算法。第二种方法是将分析中心产品首先转换到同一参考框架,然后进行加权平均得到综合产品，是IGS目前采用的方法。该方法简单灵活，轨道和钟差综合可采用类似算法，轨道综合产品在特定条件下满足动力学特性，但丧失了轨道动力学的高阶项特性。本文将使用加权平均法进行轨道综合研究。

虽然分析中心定轨策略与解算软件不同，导致精度存在明显差异，但从GPS 1506周后，分析中心轨道精度趋于稳定，WRMS曲线趋于平缓(如图1所示)，分析中心的权值也在整体上趋于稳定。

图1 分析中心轨道相对于IGS综合轨道的WRMS

1.1 IGS轨道产品的综合

基于文献[2,8,17—20]，归纳IGS轨道产品综合的主要步骤如下：①统一分析中心轨道坐标的参考框架，通常选取IERS的极移解(Bulletin A/B)或IGS分析中心的ERP均值作为“真值”，分析中心的轨道坐标根据其极移解与“真值”的差值分别绕X轴和Y轴作相应旋转；②进行Helmert转换，进一步统一分析中心的参考框架并确定分析中心的初始权；③基于加权平均得到组合轨道。

1.1.1 参考框架统一

由于不同分析中心的轨道坐标参考框架之间存在旋转、平移等系统性偏差，在轨道综合之前需先通过旋转变换消除坐标参考框架不一致的影响。本文最终轨道综合选取IGS发布的周极移解为“真值”，以当天中间时刻ERP参数为参考，计算分析中心极移解与“真值”的偏差，然后对轨道坐标作旋转变换。由于极移偏差均为小角度，则旋转变换的公式可按下式简化

(1)

转之后的分析中心卫星坐标；dXp、dYp分别为各家分析中心极移解相较于IGS发布的周极移在X、Y方向分量的差值。

1.1.2 Helmert转换定初始权

在进行极移旋转变换后，分析中心卫星坐标系统间仍存在系统偏差。以IGS发布的最终轨道为“真值”，将分析中心轨道坐标通过Helmert转换统一到相同的坐标参考框架消除偏差，并依据最小二乘准则，用间接平差法求解参数，误差方程如下

V3×N,1=B3×N,7·X7,1-L3×N,1

(2)

(3)

基于Helmert旋转后的验后方差对各分析中心进行定权

(4)

(5)

1.1.3 综合轨道合成

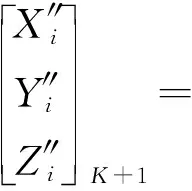
(6)

(7)

1.2 轨道综合精度评定

根据各分析中心变换处理后的坐标与综合轨道间X、Y、Z3个方向坐标分量的关系，可得各分析中心与参考轨道间的RMS及各颗卫星的RMS，公式如下

(8)

(9)

式中，mAC为分析中心AC的卫星个数。

2 试验及结果分析

按照图2流程，利用自编的轨道综合算法，利用2017年2月26日—2017年4月8日(GPS 1938—1940周)的9家分析中心事后精密轨道为试验数据，进行精密轨道综合试验。其中分别以第K周的数据作为先验观测数据，进行转换参数的求解与定权处理，对第K+1周的数据进行轨道合成。

2.1 IGS轨道产品的综合

定权结果见表1—表2，为了易于比较和分析，将分析中心ESA的权值定为单位权(1.000)。经分析得到，分析中心NGS、CODE、GFZ权值基本大于1，即相对精度较好，剩余分析中心的相对精度则稍差，其中分析中心NGS在所有分析中心的相对权值最大，即相对精度最高。该结果与IGS发布的Weighted Average图具有一致性，验证了此算法的可行性(DOY：年积日)。

2.2 轨道合成结果及分析

对GPS 1939周各个分析中心的轨道产品进行轨道综合，图3为PRN08号卫星7天内所有历元的综合轨道与IGS最终轨道在X、Y、Z方向的差值，其余卫星的效果与图3一致。图4为综合轨道、分析中心与IGS最终轨道的单天三维RMS(GPS周1939)。图5为分析中心综合轨道相对于IGS最终轨道各颗卫星单天平均三维RMS(GPS周1939)，其中PRN 04为非健康状态。表3给出了合成轨道的单天平均三维RMS(GPS周1939—1943)。

图2 轨道合成程序流程

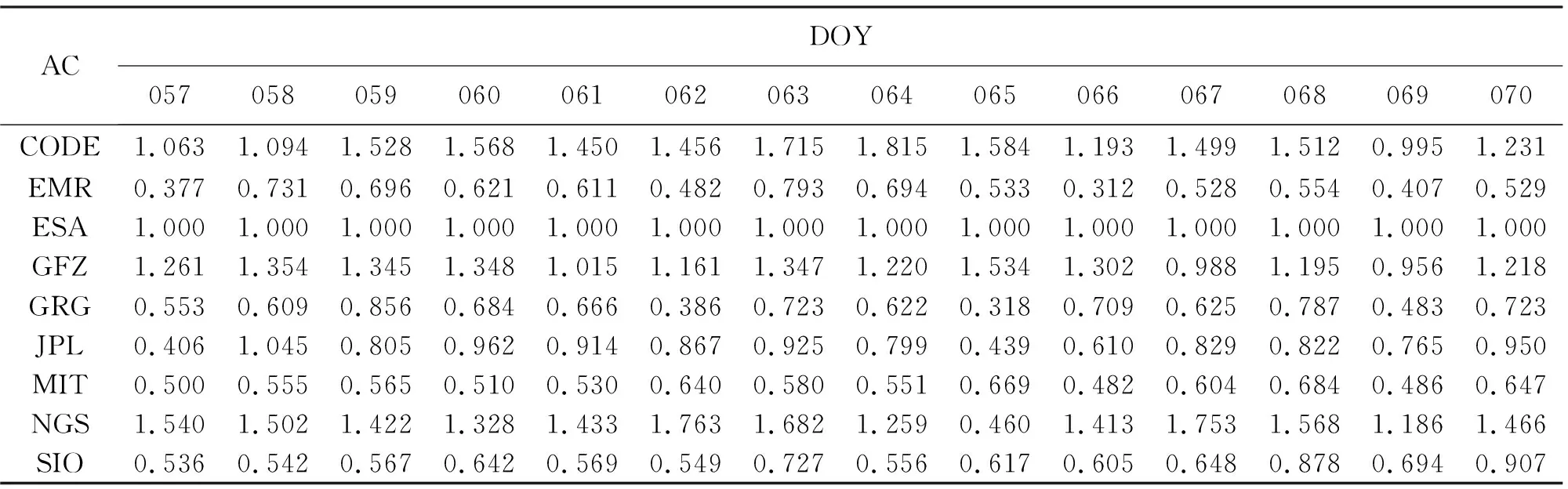
ACDOY057058059060061062063064065066067068069070CODE1.0631.0941.5281.5681.4501.4561.7151.8151.5841.1931.4991.5120.9951.231EMR0.3770.7310.6960.6210.6110.4820.7930.6940.5330.3120.5280.5540.4070.529ESA1.0001.0001.0001.0001.0001.0001.0001.0001.0001.0001.0001.0001.0001.000GFZ1.2611.3541.3451.3481.0151.1611.3471.2201.5341.3020.9881.1950.9561.218GRG0.5530.6090.8560.6840.6660.3860.7230.6220.3180.7090.6250.7870.4830.723JPL0.4061.0450.8050.9620.9140.8670.9250.7990.4390.6100.8290.8220.7650.950MIT0.5000.5550.5650.5100.5300.6400.5800.5510.6690.4820.6040.6840.4860.647NGS1.5401.5021.4221.3281.4331.7631.6821.2590.4601.4131.7531.5681.1861.466SIO0.5360.5420.5670.6420.5690.5490.7270.5560.6170.6050.6480.8780.6940.907

表2 分析中心轨道产品定权(1940—1941周)

图3 综合轨道与IGS最终轨道的差值

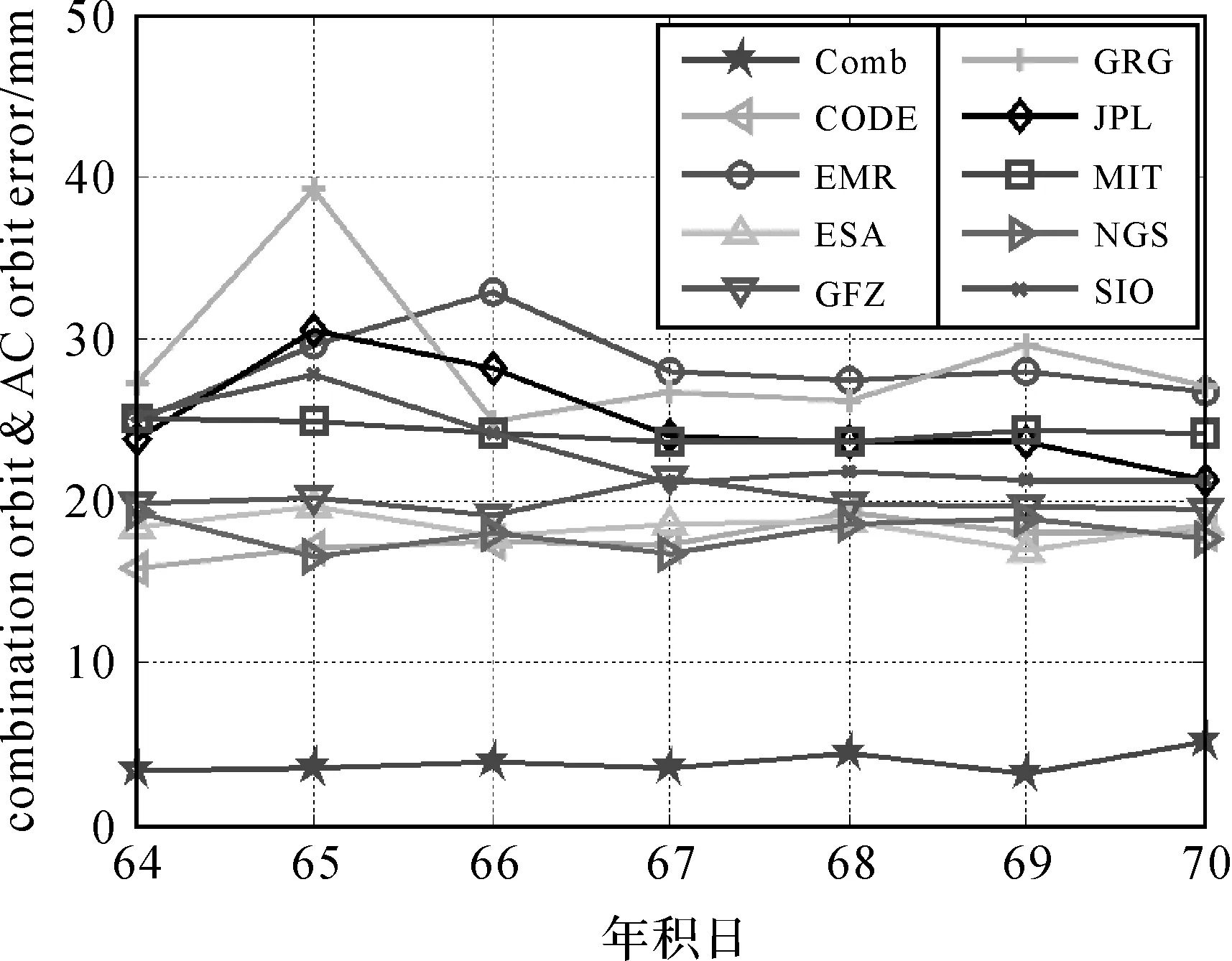
图4 综合轨道、分析中心与IGS最终轨道的单天3D RMS

分析以上数据处理结果，图4、图5表明该算法得到的综合轨道相比于各分析中心的轨道精度有显著的提高。从图4可以发现，分析中心轨道与IGS最终轨道比较的平均三维RMS均大于15 mm，即表明分析中心与IGS发布的综合轨道间存在框架差异问题。图5中表明综合轨道与IGS最终轨道相比，各GPS卫星的轨道精度在3～7 mm之间，绝大部分优于5 mm。

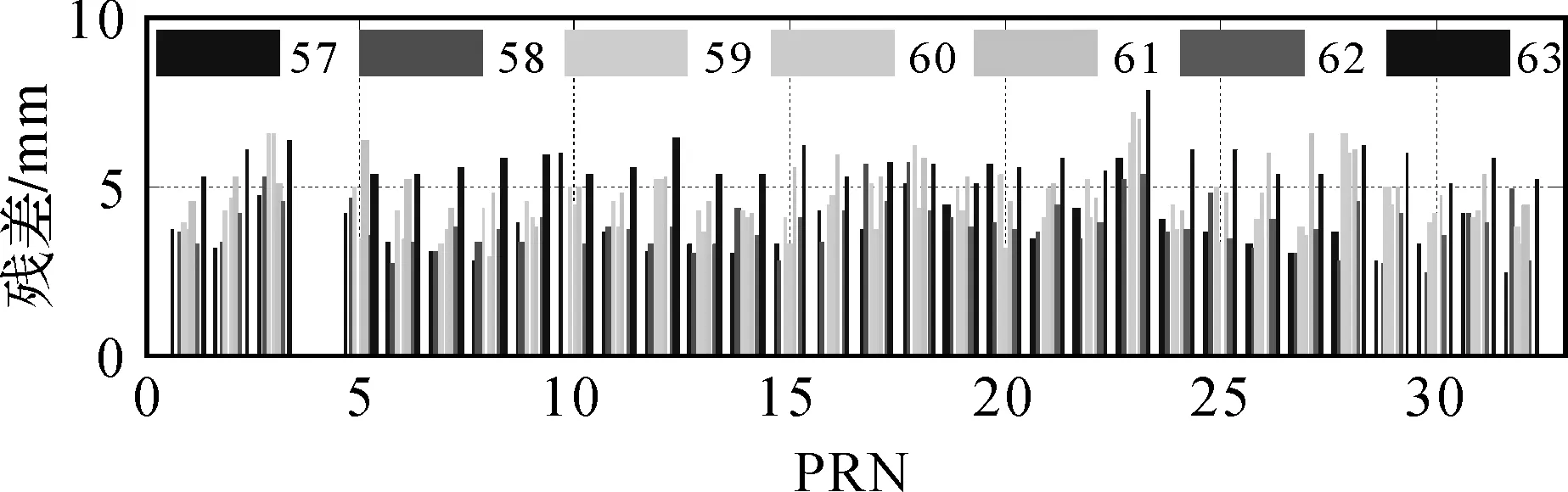
图5 综合轨道各颗卫星单天平均3D RMS

表3以周为单位，对综合轨道的整体精度进行统计计算，结果表明综合轨道单周精度优于4.5 mm，证明了对分析中心轨道产品进行加权综合的有效性。

表3 合成轨道精度统计(1939—1944)

3 结 论

本文研究了IGS分析中心轨道产品的综合方法，提出了基于IGS分析中心产品的轨道综合算法。利用自编算法对IGS各个分析中心2017年2月26日—2017年4月8日精密轨道进行综合,获得GPS综合轨道。同时以IGS最终轨道为参考，比较分析了综合轨道的精度。结果表明，IGS进行轨道综合的9个分析中心中，NGS、GFZ、CODE和ESA 4个分析中心的轨道产品精度相对较好，剩余5个分析中心的轨道产品相对较差；分析中心轨道与IGS发布的综合轨道间存在框架差异性；使用本文算法计算得到的合成轨道结果与IGS综合轨道作比较,二者三维差异小于5 mm，优于快速星历,证明了本文算法的可行性。目前，我国将建成多个北斗数据分析中心并提供轨道等各类产品，本文研究将为分析中心轨道产品的综合提供有益的参考[21]。

参考文献：

[1] DOW J M，NEILAN R E，GENDT G.The International GPS Service：Celebrating the 10th Anniversary and Looking to the Next Decade[J].Advances in Space Research，2005，36(3)：320-326.

[2] BEUTLER G，KOUBA J，SPRINGER T A.Combining the Orbits of the IGS Analysis Centers[J].Bulletin Géodésique，1995，69(4)：200-222.

[3] LI X，GE M，DAI X，et al.Accuracy and Reliability of Multi-GNSS Real-time Precise Positioning：GPS，GLONASS，BeiDou，and Galileo[J].Journal of Geodesy，2015，89(6)：607-635.

[4] SPRINGER T A，BEUTLER G.Towards an Official IGS Orbit by Combining the Results of All IGS Processing Centers[C]∥Proceedings of the 1993 IGS Workshop.[S.l.]:IGS，1993：24-26.

[5] GRIFFITHS J.Status of IGS Core Products [C]∥2013 AGU Fall Meeting.[S.l.]：IGS,2013.

[6] 李征航，黄劲松.GPS测量与数据处理[M].3版.武汉：武汉大学出版社，2016.

[7] 高成发，胡伍生.卫星导航定位原理与应用[M].北京：人民交通出版社，2011.

[8] KOUBA J，MIREAULT Y，LAHAYE F.IGS Orbit/Clock Combination and Evaluation：Appendix I of the Analysis Coordinator Report，International GPS Service for Geo-dynamics (IGS) 1994 Annual Report[M].[S.l.]：Jet Propulsion Laboratory Publication，1994：70-94.

[9] SPRINGER T A，ZUMBERGE J F，KOUBA J.The IGS Analysis Products and the Consistency of the Combined Solutions[C]∥Proceedings of the 1998 IGS Analysis Center Workshop.[S.l.]：IGS,1998.

[10] 姚宜斌.GPS精密定位定轨后处理算法与实现[D].武汉：武汉大学，2004.

[11] 施闯，邹蓉，姚宜斌，等.基于SINEX解的数据组合及系统误差分析[J].武汉大学学报(信息科学版)，2008,33(6)：608-611.

[12] 陈康慷.IGS分析中心轨道/钟差产品综合及网解模式动态精密单点定位研究[D].西安：长安大学，2014.

[13] 耿涛，徐夏炎.IGS 分析中心轨道综合算法实现及精度分析[J].大地测量与地球动力学，2017，37(4)：369-373.

[14] STEIGENBERGER P，HUGENTOBLER U，HAUSCHILD A，et al.Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J].Journal of Geodesy，2013，87(6):515-525.

[15] 谭畅，陈国，张强,等.iGMAS轨道产品综合及精度初步分析[J].武汉大学学报(信息科学版)，2016，41(11):1469-1475.

[16] CHEN Kangkang，XU Tianhe，Chen G，et al.The Orbit and Clock Combination of iGMAS Analysis Centers and the Analysis of Their Precision[C]∥中国卫星导航学术年会.西安：[s.n.]，2015.

[17] GRIFFITHS J.A Review of the IGS Final Orbit Combination Procedures (2012)，Report from the Analysis Coordinator[EB/OL].[2017-08-07].http:∥acc.igs.org.

[18] WEBER R，FRANGER E.Combination GLONASS Orbits [C]∥IGS International GLONASS Experiment IGEX-98 Workshop.Tennessee：IGS,1999.

[19] 刘伟平，郝金明，于合理,等.导航卫星精密轨道与钟差确定方法研究及精度分析[J].测绘通报，2014(5):5-7.

[20] FERLAND R，PIRASZEWSKI M.The IGS-combined Station Coordinates，Earth Rotation Parameters and Apparent Geo-center[J].Journal of Geodesy，2009，83(3)：385-392.

[21] 于素梅.iGMAS产品精度评定和一致性分析[D].西安：长安大学，2016.