红外拦截弹输出反馈制导控制一体化设计

常 晶，周 军，郭建国

(西北工业大学精确制导与控制研究所， 西安 710072)

0 引 言

制导控制一体化(Integrated guidance and control，IGC)设计方法是为了弥补传统的拦截弹制导与姿态控制分离设计的耦合效应而提出的。通过对制导环节和姿态控制环节的整体系统展开设计，制导控制一体化设计方法有效提高了导弹对大机动目标的拦截精度[1]。

IGC系统是一个具有各种不确定性的高阶系统，面临着非匹配不确定系统的控制问题[1]。目前对于IGC系统主要有两种控制思路，一种是对其线性化模型进行最优控制设计[2]，但是忽略了系统的模型不确定性和干扰的影响；另一种是将鲁棒控制方法与退步算法相结合进行制导控制一体化设计[3-7]以抑制模型的不确定性和干扰的影响。虽然以上方法解决了IGC设计中不确定性和干扰的问题，但是这些方法都假设导弹的所有状态是可测量的。 然而，采用红外导引头的拦截弹由于其导引头的特殊性，在制导控制一体化设计过程面临着新的难题：视线角速率无法获取[8]。对于这类部分状态未知的拦截弹而言，前述基于反步算法的IGC设计难以工程实现。

文献[9]中利用高增益观测器技术和输入状态稳定理论研究了导弹在视线角速率不可获取时的制导问题，但是只给出了导弹加速度指令，依然属于传统的制导控制系统分离设计。进一步，文献[9]采用高增益观测器只估计了未知状态，没有对干扰进行估计和补偿。将导弹飞行过程中的气动力参数和气动力矩参数不确定性以及风干扰和目标机动不确定性作为集总干扰，利用观测器来实现未知状态和干扰的估计，然后结合退步算法实现IGC系统的控制律设计是消除或抑制导弹不确定项影响的一种有效解决途径[3]。同传统的线性观测器不同，滑模观测器通过在观测器中引入一个非线性项可以达到有限时间的收敛，具有鲁棒性强、设计简单灵活的特点[10]。但是，要利用滑模观测器实现干扰的估计，系统的不变零点需要是稳定的(最小相位)，且系统必需满足匹配条件[10-11]。采用红外导引头的高速拦截弹的IGC系统不满足干扰匹配条件。通常有两种方法来放松匹配条件的约束，一种是通过高阶滑模微分器[10-11]得到输出变量的微分项构造扩张输出状态使得新系统满足匹配条件；另一种方法是设计多个滑模观测器的串联[12-13]，构造一个虚拟系统，直到虚拟系统满足匹配条件。高阶滑模微分器容易引入噪声的影响，且要求系统的高阶导数有界。这种串联滑模观测器的设计参数多，干扰误差容易累计。此外，这些方法适用的系统都需要满足最小相位条件。Rios等[11]将系统分为强可观子系统、可观子系统和不可观子系统，保证了非最小相位系统的估计误差有界。Bejarano[14]针对特殊的干扰研究了放松滑模观测器强可观性条件的方法。文献[15]通过坐标变换研究了不满足最小相位系统和干扰匹配条件的滑模观测器，要求的输出与干扰个数满足一定关系，其缺点是只可以实现部分干扰的估计。

基于以上分析，本文借鉴文献[14-15]的思想，通过构造补偿滑模观测器，实现了红外导引高速拦截弹在不满足干扰估计匹配条件下的未知状态和干扰的完全估计。然后，将未知状态和干扰估计信息用于拦截弹IGC系统的设计，利用李雅普诺夫函数证明了制导控制系统的有界稳定性。本文提出的方法拓展了基于滑模观测器和反步算法的制导控制一体化算法的工程适用范围，实现了采用红外导引头的拦截弹在视线角速度难以获取且存在非匹配不确定性影响下对目标的高精度拦截。最后，数值仿真结果表明了本文所设计方法的有效性。

1 问题描述

弹-目相对关系如图1所示，M与T分别代表导弹与目标，其相对运动方程为：

(1)

(2)

式中：R和q分别表示弹目相对距离和视线角，VM与VT是导弹和目标的速度，θM与θT分别是导弹和目标的弹道倾角。对式(2)求导并代入式(1)可得：

(3)

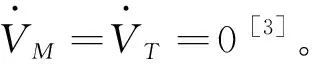
(4)

式(4)中的导弹加速度可表示为

(5)

式中：α是攻角，m为导弹质量，TM是导弹的推力，L是导弹的升力。

导弹的姿态动力学方程为[4]

(6)

式中：ϑ是俯仰角，ωz是导弹的角速率，Jz为转动惯量，δz是俯仰舵偏，M=M0+Mδzδz表示导弹的俯仰力矩。Mδz是由舵偏产生的力矩,M0为攻角、马赫数和高度等因素引起的力矩，可近似表示为M0=Mαα+Mωzωz，其中Mα和Mωz分别表示α和ωz引起的力矩系数。当α，ωz和俯仰舵偏δz较小时，升力L和力矩M可写作

(7)

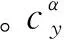
(8)

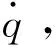
(9)

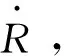
(10)

式中：

为保证拦截弹击中目标，应该设计制导控制系统使得x1=0。针对具有非匹配扰动的系统(10)，本文的目标是利用滑模观测器(Sliding mode observer,SMO)实现未知状态x1和扰动d的估计，然后结合反步算法设计出一体化的控制变量δz，使得x1=0。但是，利用常规的滑模观测器，系统必需满足(A,D,C)的不变零点稳定和扰动估计的匹配条件rank(CD)=rank(D)，而系统(2)中rank(CD)=2, rank(D)=3，不满足这个条件。下面分析如何通过滑模理论中的等效控制构造补偿滑模观测器，估计系统(10)的未知状态和干扰，实现红外拦截弹的输出反馈制导控制一体化。

2 观测器设计

根据文献[10]的附录，通过对系统x和f做一定的坐标变换，矩阵(A,D,C)可以转换为

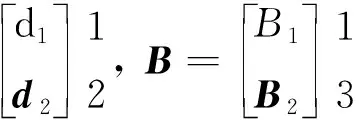
(11)

式中：

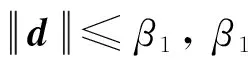
引理1[16]. 对于连续正定函数V(t)满足以下条件

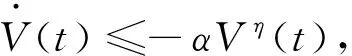
(12)

式中：α>0, 0<η<1是常数，则V(t)在有限时间到零。

系统(11)的未知状态和干扰可以由如下的滑模观测器给出

(13)

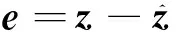
(14)

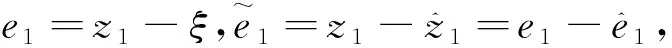
(15)

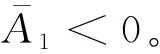
(16)

(17)

对V1从0到t积分可得

(18)

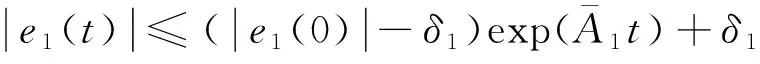
(19)

考虑到随着t→∞，式(19)中右边第一项趋于0，则h(t)→δ1。当|e1(0)|>δ1，则h(t)从|e1(0)|递减到δ1；反之，h(t)从|e1(0)|增加到δ1。因此，h(t)≤max(δ1,|e1(0)|)。令δ=max(δ1,|e1(0)|)，则估计误差e1(t)是有界的且满足|e1(t)|≤δ。

(20)

设计参数k2满足

(21)

则

(22)

(23)

(24)

(25)

(26)

3 制导控制一体化算法设计

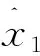
(27)

式中:η1>0是控制器增益。

2)定义跟踪误差s2=x2-x2c，设计虚拟控制量

(28)

(29)

3)定义跟踪误差变量s3=x3-x3c, 系统的实际控制量设计为

(30)

假设2.虚拟控制量x2c和x3c的导数是有界的。

定理2.考虑非线性系统(9)具有有界扰动d，如果利用观测器(13)对系统的未知扰动和舵效损失同时进行估计，然后代入式(27)～(30)所示的控制器，通过选择合适的参数，则系统状态是一致最终有界的,s=[s1,s2,s3]T将渐近地收敛到零附近的小邻域中。

证. 定义指令滤波函数的误差分别为ec1=x2c-x2d，ec2=x3c-x3d。令Lyapunov函数

(31)

其中，ec=[ec1,ec2]T。将式(27)～(30)代入式(9)，可得

(32)

对Vs求导可得

(33)

(34)

当选取ηi,i=1,2,3和τi,i=1,2使得τ2<1,τ3<1，η1>c0-2,η2>c1-3-1/τ2,η3>c2-2-1/τ3，则

(35)

式中：ξ=2min(1,2,3,4,5)

4 仿真校验

本节通过数值仿真对所设计的基于滑模观测器的输出反馈控制方法的有效性进行校验。设置拦截弹初始条件为：VM(0)=1200 m/s，VT(0)=900 m/s，α(0)=0°，ω(0)=0°/s，θM(0)=0°，θT(0)=10°，且导弹的初始位置在(0,16) km，目标的初始位置在(1,16.4) km。舵机模型是时间常数为0.01 s的一阶惯性环节且限幅为±30°。导弹的气动系数参照文献[4]：

为了进行仿真对比研究，将本文提出的基于滑模观测器的部分状态反馈BC方法 (Partial state feedback back-stepping control, PSFBC ) 和文献[8]中视线角速度未知的基于输入-状态稳定和高增益观测器的制导律 (High-gain observers based partial state feedback control, HOPFC) 分别在标称情况和气动参数摄动的情况下进行仿真校验。目标机动过载设置为5g，并且考虑导弹存在30%以内的气动参数摄动，对系统(8)分别加外界扰动：dvq=10cos(u/3)+15，dα=5sin(u/2)+3,dω=cos(u/5)+0.5。文中所提方法的观测器参数和控制器参数分别取为：K1=diag(10,10,10),k2=1,kv=1.5,η1=2,η2=2,η3=4,τ1=0.1,τ2=0.1。

图2～图3给出了标称情况存在未建模动态的仿真结果。当导弹存在30%的气动参数摄动和外部干扰情况时，其仿真结果在图4～图5给出，导弹依然实现了精确打击目标。两种制导方法在各种参数摄动以及外部扰动情况下的脱靶量和拦截时间统计结果如表1所示。从表1可以看出，本文提出基于SMO的输出反馈IGC方法达到了脱靶量小于0.1 m，打击精度高于文献[8]中基于高增益观测器的制导方法。PSFBC方法由于基于高增益观测器在初始时刻将较大的干扰估计误差引入了控制器设计中，同时其估计误差只能渐近收敛于一个小领域，因此不能完全抵消干扰和不确定性对系统的影响。而本文提出的方法，因为滑模观测器精确估计了未知状态和干扰，提高了系统的鲁棒性。标称情况下导弹对目标的跟踪轨迹在图2(a)中给出,图2(b)为两种方法的舵偏变化曲线。由于在初始时刻，高增益观测器在控制器中引入了较大的干扰估计误差，因此HOPFC算法的舵偏指令偏差较大且达到饱和，而本文采用方法所需要的舵偏角较小，且过渡过程的动态响应更平缓。到了快接近目标时，两种方法的导弹与目标碰撞角度不同，导致最后视线角速度的发散方向不同，因此，舵偏指令最后时刻差异明显。图3和图5给出了滑模观测器对未知状态Vq和干扰的估计效果，实现了各观测误差收敛到零。

5 结 论

本文提出的方法拓展了基于滑模观测器和反步算法的制导控制一体化算法的工程适用范围，对于部分状态无法获取的导弹也可实现制导控制一体化设计，精确打击目标。文中严格证明了新型SMO的有限时间收敛特性和整个IGC系统的有界稳定。仿真结果表明,导弹可以快速精确击中目标，系统具有较好的鲁棒性、动态性能和制导精度。

参 考 文 献

[1] 薛文超，黄朝东，黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用， 2013, 30(12): 1511-1520. [Xue Wen-Chao，Huang Chao-Dong，Huang Yi. Design methods for the integrated guidance and control system[J]. Control Theory and Applications, 2013, 30(12): 1511-1520.]

[2] Xin M,Balakrishnan S N, Ohlmeyer E J. Integrated guidance and control of missiles withθ-D method[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6): 981-992.

[3] 董朝阳, 程昊宇, 王青. 基于自抗扰的反步滑模制导控制一体化设计[J]. 系统工程与电子技术, 2015, 37(7):1604-1610. [Dong Chao-yang, Cheng Hao-Yu, Wang Qing. Backstepping sliding mode control for integrated guidance and control design based on active disturbance rejection[J]. System Engineering and Electronics, 2015, 37(7): 1604-1610.]

[4] Ran M P, Wang Q,Hou D L, et al. Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J]. Chinese Journal of Aeronautics, 2014, 27(3): 634-642.

[5] 齐辉, 张泽, 韩鹏鑫, 等. 基于反演滑模控制的导弹制导控制一体化设计[J]. 系统工程与电子技术, 2016, 38(3):618-623.[ Qi Hui, Zhang Ze, Han Peng-xin, et al. Integrated design of missile guidance and control based on back-stepping and sliding mode control[J]. Systems Engineering and Electronics, 2016, 38(3): 618-623.]

[6] 吴云洁, 张聪. 主从编队反舰导弹末制导段一体化位姿控制[J]. 宇航学报,2016,37(12):1315-1322. [Wu Yun-jie, Zhang Cong. Integrated control of position and attitude for terminal guidance of leader-follower anti-ship missiles[J]. Journal of Astronautics, 2016, 37(12): 1315-1322.]

[7] 赖超, 王卫红, 熊少锋. 拦截大机动目标的三维制导控制一体化设计[J]. 宇航学报, 2017, 38(7):714-722. [Lai Chao, Wang Wei-hong, Xiong Shao-feng. Integrated guidance and control design against highly maneuvering target[J]. Journal of Astronautics, 2017, 38(7):714-722.]

[8] Yan H, Ji H.Guidance laws based on input-to-state stability and high-gain observers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2518-2529.

[9] 董飞垚，雷虎民，周池军, 等.导弹鲁棒高阶滑模制导控制一体化研究[J]. 航空学报, 2013,34(9):2212-2218. [ Dong Fei-yao, Lei Hu-min, Zhou Chi-jun, et al. Research of integrated robust high order sliding mode guidance and control for missiles[J]. Acta Aeronautical et Astronautics Sinica, 2013, 34(9): 2212-2218. ]

[10] Kalsi K,Lian J, Hui S, et al. Sliding-mode observers for systems with unknown inputs: a high-gain approach[J]. AUTOMA-TICA, 2010, 46(2): 347-353.

[11] Ríos H,Efimov D, Davila J, et al. Non-minimum phase switched systems: HOSM-based fault detection and fault identification via Volterra integral equation[J]. International Journal of Adaptive Control & Signal Processing, 2013, 28(12): 1372-1397.

[12] Floquet T, Edwards C, Spurgeon S K. On sliding mode observers for systems with unknown inputs[J]. International Journal of Ada-ptive Control & Signal Processing, 2007, 21(8-9): 638-656.

[13] Tan C P,Crusca F, Aldeen M. Extended results on robust state estimation and fault detection[J]. AUTOMATICA, 2008, 44(8): 2027-2033.

[14] Bejarano F J. Partial unknown input reconstruction for linear systems[J]. AUTOMATICA, 2011, 47(8): 1751-1756.

[15] Wang X, Tan C P, Zhou D. A novel sliding mode observer for state and fault estimation in systems not satisfying matching and minimum phase conditions[J]. AUTOMATICA, 2017, 79: 290-295.

[16] Wei X J,Guo L. Composite disturbance observer based control and terminal sliding mode control for non-linear systems with disturbances[J]. International Journal of Control, 2009, 82(6): 1082-1098.