平面向量常见题型解法例析

■曹红阳

平面向量是一个具有几何与代数双重身份的概念，同时平面向量作为一种工具常与其他知识交汇命题，其考题形式灵活，解题方法多样。下面举例分析平面向量常见题型的解法。

1.平面向量的线性运算问题

例1设D为△ABC所在平面内的一点，且，则( )。

评析：平面向量的线性运算是向量运算的基础，解题时，要以向量运算的平行四边形法则和三角形法则为核心，结合几何图形，选择适当的基底，化简求解。

2.平面向量的共线(平行)与垂直问题

例 2 已知向量a=(1，m)，b=(3，-2)，且(a+b)⊥b，则m=____。

解：由a+b=(4，m-2)，(a+b)⊥b，可得4×3+(m-2)×(-2)=0，解得m=8。

评析：向量的共线问题可利用非零向量共线的充要条件a∥b⇔a=λ b进行转化求解，向量的垂直问题可应用向量垂直的充要条件a⊥b⇔a·b=0进行运算求解。

3.平面向量的数量积问题

例 3如图1所示，在△ABC中，AD⊥____。

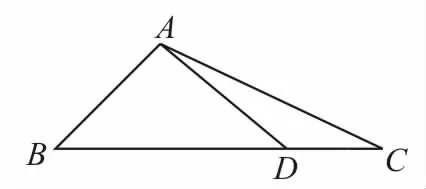
图1

评析：解答平面向量的数量积问题，关键是选择合适的基底，并把目标向量表示成基底的线性运算。

4.平面向量的综合应用问题

例4已知△ABC是边长为2的等边三角形，P为平面ABC内的一点，则()的 最小值 是____。

解：(坐标法)以BC为x轴，BC的中点为坐标原点，建立直角坐标系(图略)，则点A(0，3)，点B(-1，0)，点C(1，0)。

评析：向量具有代数特征，故可建立直角坐标系，利用坐标法求解。