平面向量的数量积的解题策略

■韩文美

平面向量的数量积通常考查数量积的确定、最值的求解等，解决平面向量的数量积的关键在于向实数进行转化。下面就平面向量的数量积的常见解题策略进行实例剖析。

一、定义法

向量a与b的数量积a·b=|a||b|·cosθ，其中θ为向量a与b的夹角，θ∈[0，π]。

例1已知向量a，b的夹角为60°，|a|=1，|b|=2，则|3a+b|=____。

解：由于|3a+b|2=9|a|2+6a·b+|b|2=9+6×1×2×cos60°+4=19，所以|3a+b|=

评析：需要注意的是求两个向量a与b的夹角θ时，要使得向量a与b的起点相同。

二、投影法

向量a与b的数量积a·b=|a||b|·cosθ的几何意义是一个向量的长度乘以另一个向量在其方向上的投影，即a·b=|a|·(|b|cosθ)或a·b=|b|·(|a|cosθ)。

例 2如图1，O是以∠BAC为钝角的△ABC的外接圆的圆心，且AB=4，AC=2，点M为BC的中点，则=____。

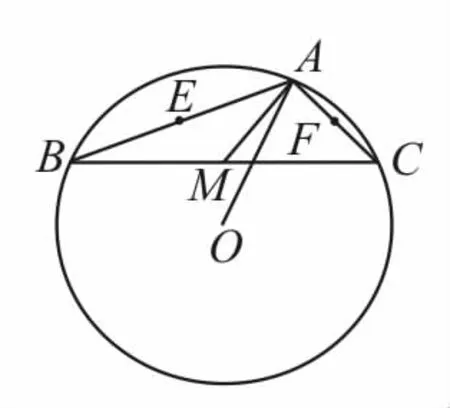
图1

解：分别取AB，AC的中点E，F，则外心O在AB，AC上的投影恰好为点E，F。所以

评析：利用投影法进行转化求解是解答本题的关键。

三、基底法

在解决平面向量的数量积时，可考虑先用合适的两个不平行的向量作为基底，将已知向量表示出来，再根据条件加以分析求解。

例3已知△ABC是边长为1的等边三角形，点D，E分别是AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为( )。

例 4已知向量a=(1，-1)，b=(6，-4)，若a⊥(t a+b)，则实数t的值为____。

解：t a+b=t(1，-1)+(6，-4)=(t+

评析：利用基底法求解是解答本题的关键，本题先选择了作为一组基底，再通过向量的线性运算加以转化求解。

四、坐标法

向量a与b的数量积a·b=x1x2+y1y2，其中向量a=(x1，y1)，b=(x1，y1)。通过已知向量的坐标或构造直角坐标系，利用坐标法来求解相应的向量的数量积问题，是比较常见的一种解题策略。6，-t-4)。因为a⊥(t a+b)，所以a·(t a+b)=(1，-1)·(t+6，-t-4)=t+6-(-t-4)=2t+10=0，解得t=-5。

评析：对于一些方便构造直角坐标系的平面向量问题，先合理构造直角坐标系，进而确定向量的坐标，再结合平面向量的数量积公式来处理。

五、平面向量的极化恒等式法

例5如图2，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，若值是____。

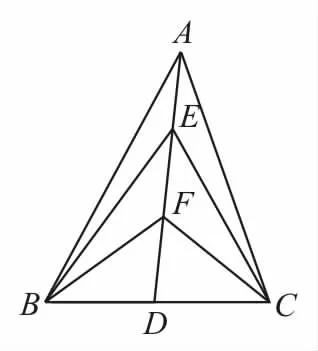
图2

评析：利用极化恒等式来解决平面向量的数量积问题，可以使解题过程简单快捷，但要注意使用时的特殊情况。

六、平面向量的三角形公式法

评析：利用平面向量的三角形公式法来处理平面向量的数量积问题，其思维独特，解题方法巧妙。

七、数形结合法

平面向量的数量积中的最值问题往往是在两个向量的方向相同或相反时取得的，而此类问题若利用数形结合法，结合直观模型，则更容易求解。

例7已知△ABC是边长为2的等边三角形，P为平面ABC内的一点，则的最小值是( )。

评析：与平面向量的数量积有关的最值问题，往往要利用数形结合法来确定点、线段、向量的位置，从而确定最值。