向量在初等数学中的应用

龚加安

Application of Vector in Elementary Mathematics

摘要：本文对向量在初等数学中的应用进行了研究。通过具体实例说明向量在初等数学各分支中的应用，揭示向量在初等数学中的重要性。

Abstract： In this paper， the application of vectors in elementary mathematics is studied. The application of vector in elementary mathematics is given by some examples， and the importance of vector in elementary mathematics is revealed.

关键词：向量；函数最值；平面几何；立体几何；三角函数

Key words： vector；functions range；plane geometry；solid geometry；trigonometric function

中图分类号：O151.24 文献标识码：A 文章编号：1006-4311（2018）15-0224-04

0 引言

向量是基础数学中重要的内容之一，它在数学的各个分支的研究中发挥着重要作用。向量有方向，可以刻画直线、平面、切线等几何对象；向量有长度，可以刻画长度、面积、体积等几何度量问题。向量的大小反映了其数的特征，方向反映了其形的特征。向量是集数、形于一身的数学概念，是数学中数形结合思想的典型表现。因此在向量的教学中要注意数与形的结合、代数与几何的结合、逻辑思维与形象思维的结合。它不仅能解决数学学科本身的问题，而且能跨学科应用，向量在物理和工程技术中的应用很广泛。许多代数、几何、三角及物理中的问题都可以转化为向量问题来处理。向量在初等数学中具有重要作用，它几乎与初等数学中几何内容与部分代数内容都有联系，在解决一些问题时显得特别简捷，因此受到很多解题者的关注与浓厚的兴趣。数学教学中要站在方法论的高度对某一板块进行整理、归结与概括，因此将向量与其它知识点结合应用更能体现向量的使用价值。

1 向量在函数中的应用

1.1 求函数最值

函数最值的求解是函数中的重要内容之一，也是不等式知识的一个重要应用，涉及的知识面广，解题技巧性强，方法也因题而异，而向量是沟通代数与几何的一种有效工具。对一些代数中有关函数最值的问题，如果能巧妙地构造向量，利用向量的方法解决，就能给人焕然一新的感觉。

2 向量在平面几何中的应用

平面几何经常涉及距离（线段长度）、夹角问题，而平面向量的运算，特别是数量积主要涉及向量的模以及向量之间的夹角，因此我们可以用向量方法解决部分几何问题。解决几何问题时，先用向量表示相应的点、线段、夹角等几何元素；然后通过向量的运算，特别是数量积来研究点、线段等元素之间的关系；最后再把运算结果“翻译”成几何关系，得到几何问题的结论。

2.1 在三角形中的应用

2.1.1 用向量表示的三角形的“心”

近几年的高考题中不断出现用向量表示的三角形“心”问题，因此，用向量的眼光透视三角形的“心”，进而解决与之相关的问题，就显得尤为重要。这里主要讨论向量表示三角形重心的应用。

解题回顾：本例题主要考察平面向量的加法运算的平行四边形法则及向量的数乘运算，考查学生分析问题和解决问题的能力，入口浅且宽广，寓意深且独特。

2.3 向量在解析几何中的应用

向量的坐标表示使向量与解析几何建立了一定的联系，也改变了解析几何中一些传统的研究方法。向量的坐标表示方法使方程思想有了更广泛的应用，同时，运用向量的数量积简化了解析几何中两直线夹角的计算。

2.3.1 与直线的综合应用

例（2003年新课程，理21文22） 已知常数a>0，向量c=（0，a），i=（1，0），经过原点O以c+λi为方向向量的直线与经过定点A（0，a），以i-2λc为方向向量的直线相交于点P。其中λ∈R。试问是否存在两个定点E、F，使得PE+PF为定值。若存在，求出E、F的坐标；若不存在，请说明理由。

解：根据题设条件，首先求出点P坐标满足的方程。据此再判断是否存在两定点，使得点P到两定点距离的和为定值。

∵ i=（1，0），c=（0，a），∴ c+λi=（λ，a），i-2λc=（1，-2λa）

因此，直线OP和AP的方程分别为λy=ax和y-a=

-2λax。

消去参数λ，得点P（x，y）的坐标满足方程y（y-a）=

-2a2x2，

由上可见，通过构造单位向量，充分体现了单位向量的独特功效，使问题解决起来直观、方便。

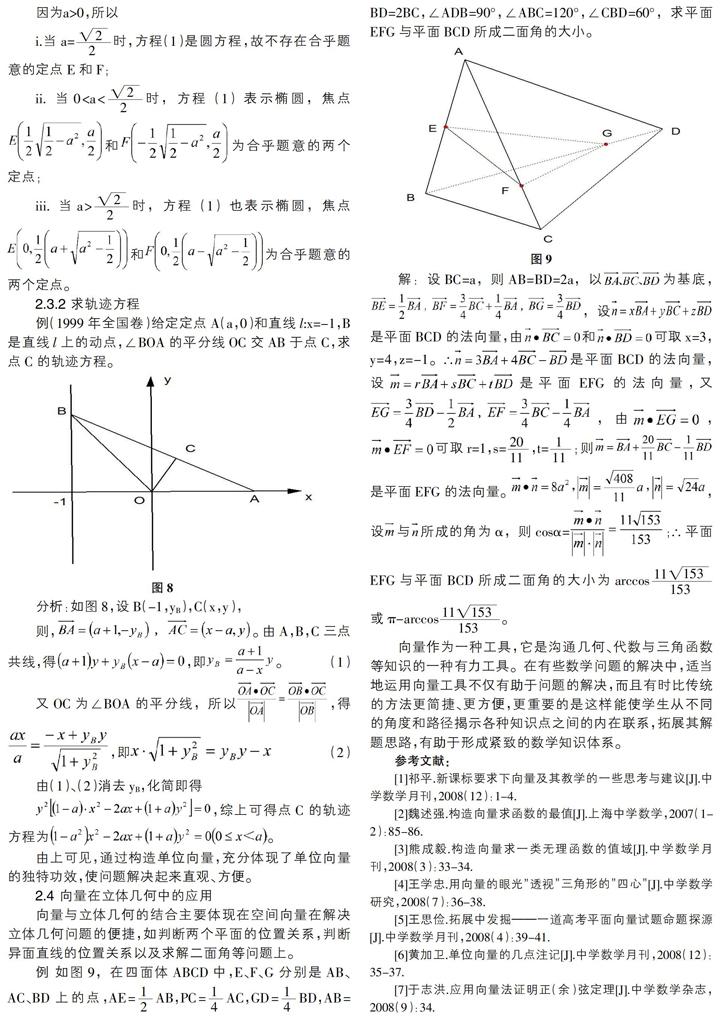
2.4 向量在立体几何中的应用

向量与立体几何的结合主要体现在空间向量在解决立体几何问题的便捷，如判断两个平面的位置关系，判断异面直线的位置关系以及求解二面角等问题上。

向量作为一种工具，它是沟通几何、代数与三角函数等知识的一种有力工具。在有些数学问题的解决中，适当地运用向量工具不仅有助于问题的解决，而且有时比传统的方法更简捷、更方便，更重要的是这样能使学生从不同的角度和路径揭示各种知识点之间的内在联系，拓展其解题思路，有助于形成紧致的数学知识体系。

参考文献：

[1]祁平.新课标要求下向量及其教学的一些思考与建议[J].中学数学月刊，2008（12）：1-4.

[2]魏述强.构造向量求函数的最值[J].上海中学数学，2007（1-2）：85-86.

[3]熊成毅.构造向量求一类无理函数的值域[J].中学数学月刊，2008（3）：33-34.

[4]王学忠.用向量的眼光”透视”三角形的”四心”[J].中学数学研究，2008（7）：36-38.

[5]王思俭.拓展中发掘——一道高考平面向量试题命题探源[J].中學数学月刊，2008（4）：39-41.

[6]黄加卫.单位向量的几点注记[J].中学数学月刊，2008（12）：35-37.

[7]于志洪.应用向量法证明正（余）弦定理[J].中学数学杂志，2008（9）：34.