剖析全国高考试题 透视数学问题本质

赵文平

(重庆市巴蜀中学 400013)

2016年高考理科全国卷Ⅱ和卷Ⅲ的排列组合问题新颖有趣，表面上卷Ⅱ考查的是实际模型中的几何组合计数问题，卷Ⅲ考查的是纯数学的数列新定义计数问题，而如果站在更高的观点上，可以发现两题同根同源，其实本质上都是考查的是组合数学上的卡特兰数的应用.

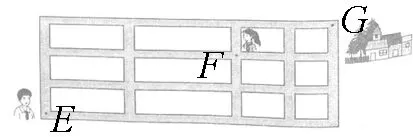
图1

例1 (2016年娄学全国卷Ⅱ)如图1，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为( )

A.24 B.18

C.12 D.9

例2 (2016年数学全国卷Ⅲ)定义“规范01数列”{an}如下：{an}共有2m项，其中m项为0，m项为1，且对任意k≤2m,a1,a2,…,an中0的个数不少于1的个数.若m=4，则不同的“规范01数列”共有( )

A.18个 B.16个 C.14个 D.12个

解析依题意，当m=4时，数列{an}共有8项：4项为0,4项为1.且对任意k≤8，a1,a2,…,ak中0的个数不少于1的个数(即从左到右数，0的累计数不小于1的累计数).分析易得a1=0，a8=1。再采用树形图列举，可知满足题意的数列{an}共有14个.

问题若高考真题2问的是对于任意的m∈N+，则不同的“规范01数列”共有多少个呢？

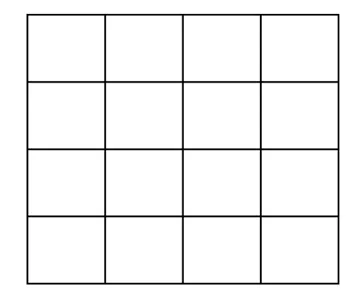
图2

要解决这个一般的问题，就必须理解这个纯数学问题的实际模型，其实高考真题2也可以理解为高考真题1实际模型的几何组合计数问题，具体理解如下：有一个4×4方格，一个质点开始在(0,0)(最左下角顶点处)，每次走一步，向右走一步记为0，向上走一步记为1，最终要运动到(4,4)(最右上角顶点处)(且要保证该质点始终处于对角线y=x之下(含对角线))的最短路径的条数.

其实，我们可以将问题推广到更一般的情况：将m个红球，n个白球排成一排，要求任意位置及其左边的红球总数不小于白球总数，共有多少种排法？

可等价转化为：存在一个m+n元数组(a1,a2,…,am+n)，其中

ai∈{0,1},i=1,2,…,m+n,且有m个1，n个0(m≥n).

记Ai={k|a1,a2,…,ai中有k个1}，Bi={k|a1,a2,…,ai中有k个0}，且Ai≥Bi对∀i=1,2,…,m+n都成立.问这样的数组共有多少个？

证明设点Pi(Ai,Bi)(i=0,1,2,…,m+n).

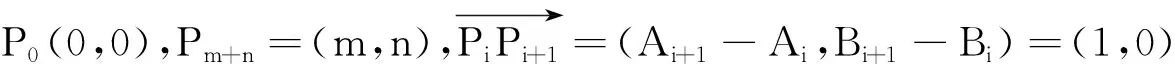
若其满足题意，则其路径必在直线y=x的下方(含直线y=x).

记A={从P0到Pm+n不满足题意的路径}，B={从P0到Pm+n的总路径}.

评注至此，我们给出了这个问题的完整解答.如果我们继续向上追问，就会发现此题的背景其实是组合数学中的“卡特兰数”(“卡特兰数”源于比利时数学家卡特兰在研究凸n+2边形的剖分时得到的数列Cn，在组合数学、信息学、计算机编程等方面都有广泛的应用；卡特兰问题的解决过程大量应用了映射方法，堪称计数的映射方法的典范.)，这就找到了问题的本质.从而也更加佩服高考命题人的良苦用心，原来2016年这两个排列组合题都同根同源，可以看成是一个复杂数学问题的两个特例.这样的命题对活跃学生思维，提高解题能力给与了很好的导向.

总之，本文通过列举2016年高考理科全国卷Ⅱ和卷Ⅲ的两道有关排列组合问题的高考真题，进行剖析、解答找到了问题的本质.原来这两个排列组合考点的试题本是同根同源，是一个复杂数学问题的两个特例.这样的高考命题将会进一步培养学生的思维能力，提高解题技巧，所以，我们在平时的教学中要特别重视这方面的引导.

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2014.

[2]夏钰钦.实现数学课堂教学有效性的五大要领[J].课程·教材·教法，2016(8):38-42.

[3]赵绪昌.数学课堂教学中教师的引导策略[J].中学数学，2012(6).

[4]凌明灿.论数学教师如何成为有效的课堂“引导者”[J].中学数学，2011(01).