一道高中学业水平考试题引发的思考
2018-06-02 08:25:49陈晓江
数理化解题研究 2018年13期
陈晓江
(四川师范大学附属昆明实验学校安宁校区 675300)
一、考题剖析
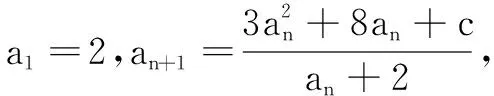
1.初步解题
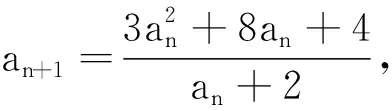
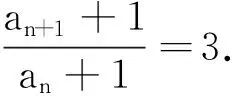
2.无中生有,“淘气”的等号
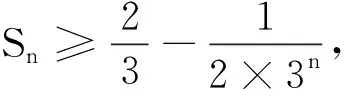
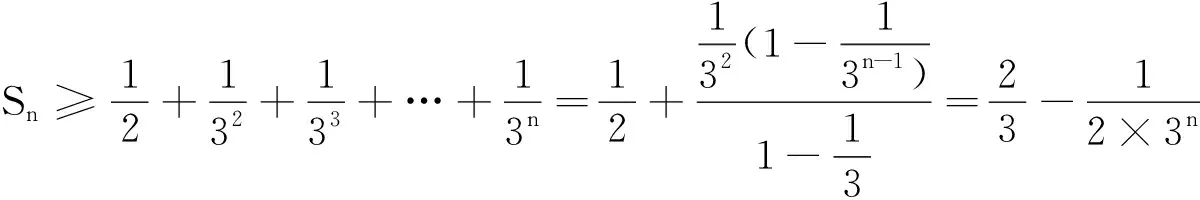
这样我们就证明出了左边的不等式.
3.执果索因,放缩有度
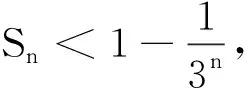
由这个例,我们深有体会,在运用放缩法求证不等式时还要注意放缩的尺度,尺度过大或过小都可能与求证结果相差甚远,只有耐心分析求证结果,由结果去寻找线索,多多尝试,做一些细微的调整,才能有精确的解答.
二、对普通高中学业水平考试数学科目的思考
我省学考的试题难易适当、题量适度.但这并不意味着不会出现有难度的题目,笔者在前文中所举的例子在证明难度上甚至超过云南省2013届第一次高中毕业生复习统一检测理、2014年新课标全国卷Ⅱ理中所出现的数列证明题.虽然这只是偶尔出现的难题,但这并不是偶然.早在2011年1月的学考数学卷中我们就领略了压轴题的难度.这些题目的出现,打破了学生甚至教师对高中学业水平考试数学考试的原有认识,也使得教师在教学中更关注高中学业水平考试的考前复习.
参考文献:
[1]陈晨.高中数学解析几何高考试题分析与教学策略研究[J].新课程:中学,2016(10):223-224+226.
[2]李彦.由两道高考数学真题解析引发的启示与思考[J].中学数学,2015(07):80-81.
猜你喜欢
红蜻蜓·高年级(2022年6期)2022-06-16 02:53:58
中学生数理化·自主招生(2022年2期)2022-05-30 10:48:04
小天使·四年级语数英综合(2022年4期)2022-04-28 17:48:58
中学生数理化(高中版.高考理化)(2022年2期)2022-04-26 14:01:52
中等数学(2020年4期)2020-08-24 08:08:40
疯狂英语·新悦读(2019年12期)2020-01-06 03:28:06
中学语文(2019年34期)2019-12-27 08:03:46
中学数学杂志(2019年1期)2019-04-03 00:35:36
阅读(低年级)(2018年11期)2018-05-14 09:37:53
作文·初中版(2015年11期)2015-12-02 16:54:14

