培养提问技能发展问题探究能力——以探究轻杆上的弹力方向为例

陈 艳

(陕西省西安市西光中学 710001)

美国教育家杜威曾指出:问题存在于人们遇到困难时.心理学家纽厄尔与西蒙提出:问题是个体想做某件事,但不能即刻知道做这件事所需要采取的一系列行动.对于学生来说，问题是始终存在的.在教学活动中，学生常常会提出一些经过思考而得出的具有一定难度的问题，这些问题足以让学生进行一番苦苦思考，甚至无法自主得出结论.相比于直接回答学生的问题，教师更应对学生进行必要的训练，使学生通过可以实施的步骤将自主发现的问题聚焦为核心问题，并且能够持续的探究和自我追问，逐渐深度建构自己的问题体系，最终自主解决问题.下面以学生对轻杆模型弹力方向提出的问题为例，分享笔者在教学中尝试教会学生提问技能，促进学生自主解决问题的教学策略.

一、问题的提出

高中物理教学中，共点力的平衡是重点内容，常以轻绳、轻杆来建构题目情境，典型题目如下：

例1 如图1，轻杆OD的OC段长为L，CD段嵌入墙壁固定，O端固定一个光滑的定滑轮，轻绳AB一端固定在墙壁上的A点，另一端跨过定滑轮在B处悬挂质量为M的重物，系统保持静止，则OD杆对绳的作用力的大小和方向如何？

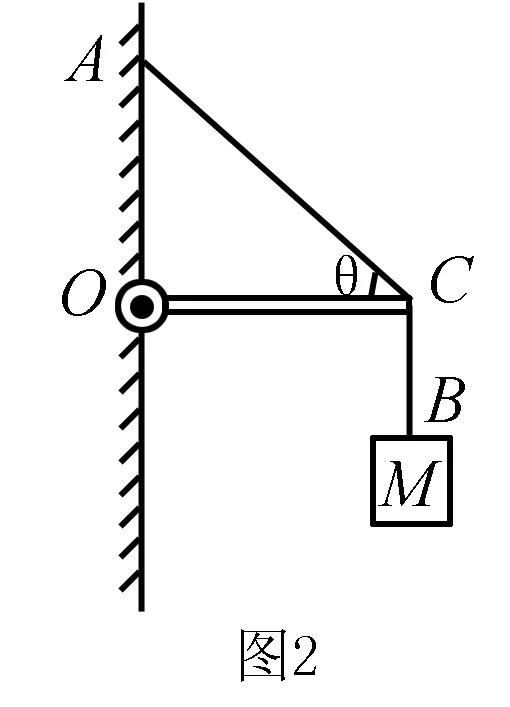
例2 如图2，长为L的轻杆OC，C端用光滑铰链与墙壁固定，轻绳AO一端固定在墙壁上的A点，另一端与杆的O端相连，轻绳BO一端与杆的O点相连，另一端在B处悬挂质量为M的重物，系统保持静止，则AO绳上的弹力大小如何？这两类典型题目强调了轻杆模型的特征：杆上的力不一定沿杆向.但学生也因此产生了极大地困惑：例一情境中可以由共点力平衡条件计算出杆上的力不沿杆向；但例二情境中，由共点力平衡条件计算绳AO上的弹力大小时，怎么能确定CO杆上的力沿着杆向呢？什么情况下杆上的弹力方向一定沿杆向？

二、 对问题进行分析，确定教会学生提问技能，促进学生自主解决问题的教学策略

高中物理不涉及刚体平衡的知识，教师通常会直接告诉学生“若轻杆的一端是以光滑铰链固定的，则杆上的弹力沿杆向”.事实上，平衡状态杆上的弹力具体沿什么方向是由平衡条件和受力环境决定的，是遵循物理规律的.学生真正的困惑在于轻杆上弹力方向怎样确定.解决这个问题，学生需要具备初步的刚体平衡的知识；需要有解决平衡问题的一般策略性方法；要应用受力分析、力的分解与合成等具体物理方法；要进行较复杂的数学运算等，是个比较复杂的思维过程.因此，在教学中要注重教会学生提问技能，使学生通过可以实施的步骤将自主发现的问题聚焦为核心问题，并且能够持续的探究和自我追问，逐渐深度建构自己的问题体系，最终自主解决问题.结合学生的实际情况确定教学策略如下：

1.要求学生书面描述问题，明确问题实质

学生提问通常是拿着题目直接来问，问的过程中会将另一种情境的问题提出来进行对比，但因为是口头表述，所以对细节的描述常常含糊不清，甚至错误，这会直接影响学生的自主思维，因此，训练学生的提问技能的第一步应该是要求学生明确描述问题，而让学生书面描述问题可以有效的达到这个目的.

2.要求学生确定解决问题的方案，明确追问策略

策略性知识是程序性知识的一种，能够提高人的认知效率，“到了初中和高中时期，策略发展处于后期阶段，某些青少年在他们熟悉的知识领域，可以在无成人指导的条件下，自觉运用适当的策略改进学习，而且能根据任务的需要来调整策略” .高中生掌握追问策略有利于学生进行自我追问，实现对问题解决的过程的自我监控和及时调整.

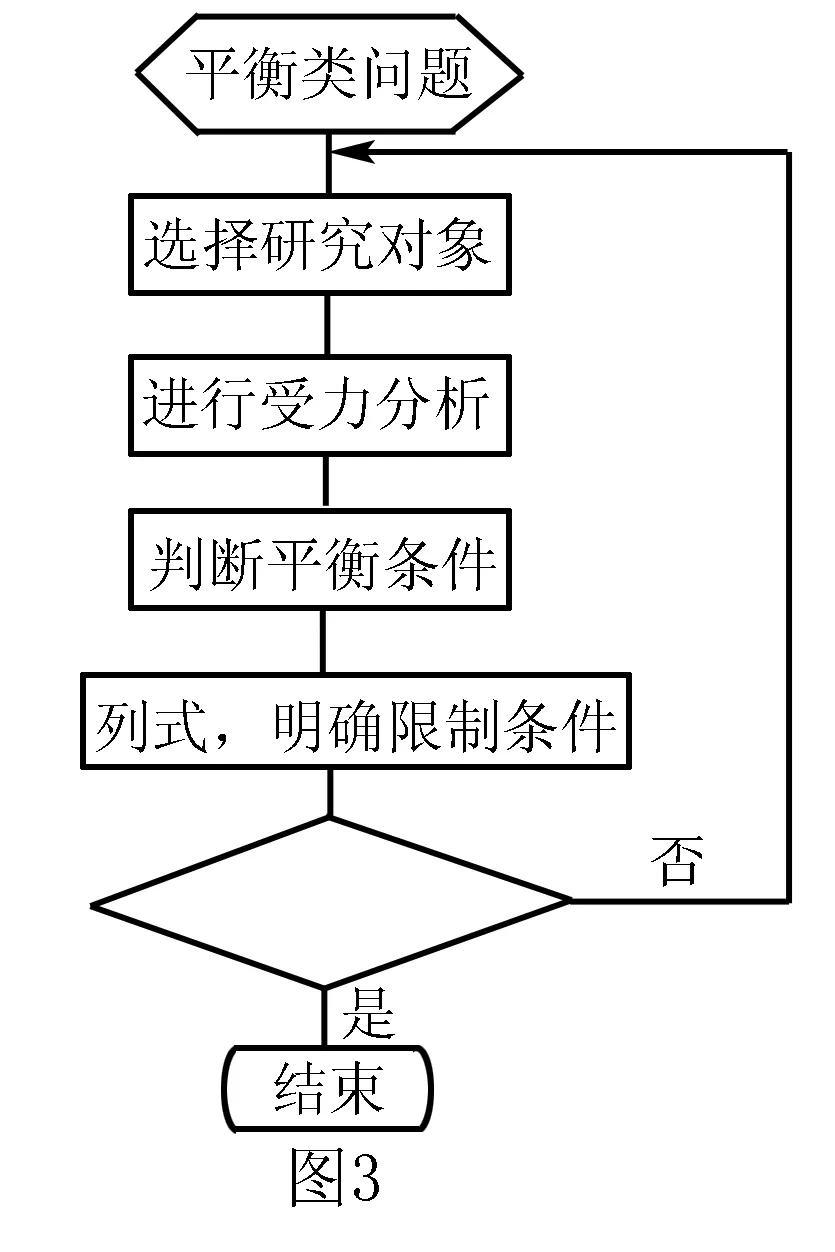
高中物理解决平衡类问题的方案是由一些相对固定的步骤和方法组成的，确定这些步骤和方法，对学生的自我追问能够起到支撑作用，便于将复杂问题分解为更具体的子问题，便于学生明确探究困难到底是什么，利于学生寻求有效的帮助，不会因无法解决具体问题而怀疑解决问题的一般策略.具体流程如图3所示.

3.要求学生将思维可视化，支撑自我追问过程

“教师应当有意识地将自己的思维过程明明白白地展示给学生.”是一种有利于教会学生思维的方法.将思维环节明确出来，能够支撑学生的自我追问活动，同时将解决子问题的过程嵌入到解决平衡类问题的一般思维体系中，更利于学生深度建构问题体系.要求学生按照前面确定的解决问题的一般策略完成子任务，以此来支撑自我追问.

4.要求学生通过各种途径解决追问过程中的具体子问题，并进一步自我追问，寻求帮助，突破难点.

轻杆的平衡条件并不是难点，学生通过查找资料，结合初中的杠杆原理以及个别提问很快了解了轻杆的平衡条件；难点表现为选择力的运算法则：用力的平行四边形定则，还是选用正交分解对力进行运算；不能顺利的求解方程组.教师通过引导学生比较，去发现选择力的不同运算法则只影响数学计算式的形式及运算的简繁程度，物理作用是相同的，促使学生进一步理解这些零散的知识并将其纳入知识体系.至于解方程组，也是一个物理教学实际中面临的难点，必须正视这个问题，要进行解方程组的策略引导和实际操作的演示.

三、进行提问技能的训练，促进深度建构问题系统，实现自主学习

1.对例一(如图1)的探究

提出问题并按策略流程解决问题：“例一(如图1)中OD杆对绳的作用力的方向是否沿杆向？”

环节一、研究对象：O处与滑轮接触的一小段绳

环节二、受力分析：以等效的观点，用沿杆向的分力FX和垂直与杆向的分力Fy等效替代杆对绳的力如图4

环节三、平衡条件：共点力平衡，可用正交分解

环节四、列方程并明确限制条件：

FNx=FAcosθFNy+FAsinθ=FBFALsinQ+M=FBL

限制条件：FA=FB=Mg，解方程可知两分力均不为零，故不沿杆向

环节五、判断能否解决问题：问题已经解决，就题目来说已经可以结束了，但还可以对杆进行进一步分析，看看为什么杆上的力不沿杆向.

继续提出问题：为什么杆上的力可以不沿杆向？

环节一、研究对象：轻杆

环节二、受力分析：因杆嵌入墙壁，故墙壁可以对杆提供所需方向的力如图5

环节三、平衡条件：共点力平衡、力矩平衡

环节四、列方程并明确限制条：

FNx=FAcosθ(3)

FNy+FAsinθ=FB(4)

FALsinθ+M=FBL(5)

限制条件：FA=FB=Mg.解方程可知墙壁对杆两分力均不为零.

环节五、判断能否解决问题：因为杆是嵌入墙壁的，故墙壁对杆能够提供不为零的力，且该力可以不过转轴C，产生逆时针力矩M，故，杆上的力可以不沿杆向.问题得到解决.

总结：因固定端可以提供不经过转轴的力，故嵌入墙壁固定的轻杆上的力可以不沿着杆向

2.对例二(如图2)的探究

提出问题并按流程解决问题：OD杆对绳的作用力的方向是否沿杆向？

环节一、研究对象：结点O

环节二、受力分析：以等效的观点，用沿杆向的分力Fx和垂直与杆向的分力Fy等效替代杆对结点O的力如图6

环节三、平衡条件：共点力平衡，可用正交分解

环节四、列方程并明确限制条：

Fx=FAcosθ(1)

Fy+FAsinθ=FB(2)

无特殊限制条件.

环节五、判断能否解决问题：不能确定Fx、Fy是否为零，故问题还没有解决，策略性知识可知还应再添加研究对象，也就是对杆进行进一步分析

继续提出问题，并按流程解决问题：

患者眩晕症状全部消失，不影响患者的正常工作及生活，随访2个月无复发评价为显效；患者眩晕症状有显著改善，头疼现象有明显减轻，随访2个月发作频率较之前有明显减少评价为有效；达不到上述标准者评价为无效。临床总有效率=显效率+有效率。

环节一、研究对象：轻杆

环节二、受力分析：如图7

环节三、平衡条件：共点力平衡；力矩平衡

环节四、列方程并明确限制条：

FNx=FAcosθ(3)

FNy+FAsinθ=FB(4)

FALsinθ+M=FBL(5)

限制条件：FN过转轴C，即FN对转轴产生力矩M为零

环节五、判断能否解决问题：比较第(2)式和第(5)式，可知Fy=0，即杆对结点的弹力沿杆向；比较第(4)式和第(5)式，可知FNy=0，即固定轴对杆的弹力也沿杆向；问题得到解决.

总结：因固定端只能提供经过转轴的力，故杆上的力沿着杆向

3.学生提出新问题，由轻杆构成的三角形支架如图8，为什么杆上的弹力方向也沿杆向？

环节一、研究对象：结点O；明确三角形支架的固定方式是点固定，也就是墙壁只能对A、C两处固定点有力的作用

环节二、受力分析：这个情境中有两根轻杆，杆上的力方向不能确定时，仍以等效的观点，用沿杆向的分力F1和垂直与杆向的分力F2等效替代杆对结点O的力，如图9.

环节三、平衡条件：共点力平衡，可用正交分解

环节四、列方程并明确限制条：沿OC杆和垂直与OC杆分解

FA1cosθ=FA2sinθ+FC1(1)

FA1sinθ+FA2sinθ+FC2=FB(2)

限制条件：无特殊限制条件，且由上式不能计算FA2和FC2的值

环节五、判断能否解决问题：不能判断各杆杆对O点的力是否为零，还应再添加研究对象进一步分析，继续按流程处理：

环节一、研究对象：轻杆OC

环节二、受力分析：如图10

环节三、平衡条件：共点力平衡、力矩平衡

环节四、列方程：

FNAx+FA2sinθ=FA1cosθ(3)

FNAy+FA1sinθ+FA2cosθFB(4)

FA1LCsinθ+FA2LCcosθ+M=FBLC(5)

环节五、判断能否解决问题：FNC过转轴C，即FNC对转轴产生力矩M为零比较第(2)式和第(5)式，可知FC2=0，比较第(4)式和第(5)式，可知FNcy=0，OC杆的弹力沿杆向.但不能判断AO杆的弹力方向，还应再添加研究对象进一步分析.

总结：因OC杆的固定端只能提供经过转轴的力，故杆上的力沿着杆向.

同理，对轻杆OA进行分析：

环节一、研究对象：轻杆OA

环节二、受力分析：如图11

环节三、平衡条件：共点力平衡力矩平衡

环节四、列方程并明确限制条：

FNAx=-FC1(6)

FNAy+FC2=FB(7)

FC2LAsinθ+FC1LAsinθ+M=FBFAcosθ(8)

限制条件：FNA过转轴A，即FNC对转轴产生力矩M为零；FC2=0；

由第(8)式得：FC1sinθ=FBcosθ(9)

代入(1)(2)式得

FA1cosθsinθ-FA2sin2θ=FA1sinθcosθ+FA2cos2θ

即：FA2=0

环节五、判断能否解决问题：OA杆的弹力沿杆向.可进一步分析出FNA也沿杆向.

总结：因OA杆的固定端只能提供经过转轴的力，故杆上的力沿着杆向.

最后学生按照这个流程又进一步对三角行支架的一般受力条件下的弹力方向进行探究.最后得到结论： “若轻杆的一端是以光滑铰链固定的，则杆上的弹力沿杆向”是因为固定端只能提供经过转轴的力，应用轻杆的平衡条件，通过计算确定出杆上的力沿着杆向.严格意义上，确定杆上的弹力方向必须通过计算，但上述情境有共同特点：(1)轻杆的一端是以光滑铰链固定的;(2)轻杆只在两个端点受力，故今后做题若遇到这类情境即可迅速判断杆上的力沿着杆向.

这个探究过程困难重重，但事实表明，学生在一般的策略性知识的支撑下，区分各子任务，分项解决问题，最终完成探究任务并将问题进行了拓展探究，取得了很好的成果.这种做法充分体现了学生的主体性，营造了开放的教学空间，有利与真正实现学生学习的可持续发展.

参考文献：

[1]林玉坤.如何培养老师的问题探究教学能力[M].桂林:漓江出版社,2011(07).

[2]皮连生.教与学的心理学[M].上海:华东师范大学出版社,2009:106-107.

[3]郅庭瑾.教会学生思维[M].北京:教育科学出版社,2002:138.