高中数学函数解题思路多元化的方法研究

董哲坤

(山东省泰安第一中学2016级15班 271000)

高中数学是高中阶段的重要学科，也是同学们学习过程中常常遇到问题的科目，尤其是在学习函数的过程中，函数题目本身变化的多样性让很多同学感觉棘手，不能真正掌握其解题的方式，解题能力得不到本质的提高.因此，本文在分析高中数学函数解题现状的基础上，以日常学习中常见的题目为例进行探讨，希望能够切实帮助同学们在高中函数解题思路方面得到多元化提升，进而提高学习效率，以获得理想的成绩.

一、高中生函数解题现状

从目前情况来看，同学们在函数解题方面存在较为明显的不足.首先，部分同学对于函数的含义理解不够透彻，在基本概念学习时没有掌握扎实，真正明白其本质含义，前期学习的模糊就导致在后期具体解题过程中无法抓住题目的要点和解题点；其次，部分同学在函数解题方面的思维不够活跃，在解题过程中往往是用课本上的固定形式进行套用，如果出现变化则很难快速找到解题思路，无法正确理解题目的意图和考查的知识点.最后，部分同学由于本身知识体系不够完善，在函数解题过程中需要同时运用多个知识点时，会因知识体系的缺失导致在函数解题过程中很难灵活运用多种思路.

二、函数多元化解题思路的方法研究

从目前的函数学习模式来说，大多是先学习基础性概念，然后以课本上的固定习题作为主进行练习，借此将课本知识、概念转变为具体的解题思路和方法.然而，课本上的习题在解体方式上较为固定，同学们在课本以外所接触的函数问题，形式变化却复杂多样，使得课本学到的解题思路无法直接运用，从而导致无法快速找到解决问题的方法，影响同学们的学习成果.因此，同学们需要从多样化的角度入手来不断提高解题能力，掌握更加全面和灵活的方法.

1.关注多种解题方式，发散思维

在高中函数的学习过程中，课本以及其他练习册上的题目大多只有一种解题方式，在多次反复的练习中也容易将思维固化，认为此类题目只有这样一种解题方式，但是从函数本身的特点来说，大多都有两种甚至多种解题方式，只是由于日常的学习习惯，并不会针对某种题目进行深究，探寻不同的解题技巧而已.同学们可以在日常的学习过程中，掌握基本解题方法的同时还应当积极思考其他的解题思路和技巧，充分结合课本上的基本概念和定理，从而抓住函数问题的本质.通过这样的方法以及练习，同学们可以在日常学习中不断培养自己的发散思维能力，加强对题目的理解和解读.需要注意的是，针对一个题目进行多种思路的解题，虽然可能花费更长的时间，但却极有必要，同学们切莫在日常学习中盲目追求做题数量而忽略了对于解题方法的探究.

2.积极运用逆向思维

同学们在接受传统教育的过程中，大多采用正向思维模式来思考问题.虽然该种思维方式能够帮助同学们解决所遇到的大多数问题，但其同时存在一定的不足.同学们在学习高中数学、解决函数问题的时候，还需要合理运用逆向性思维，突破传统思考问题的角度，提高解题的效率与正确率.因此，在高中函数的学习和练习过程中，同学们在传统正向思维找不到解题思路的情况下，可以尝试运用逆向思维的方法，这也有利于锻炼自己的综合思维能力.同时，在传统思维方式能够解题的情况下，也可以让自己从逆向思维的角度进行思考，增加思维的活跃度.

例已知向量a=(1,2),b=(x,1),u=a+2b,v=2a-b,并且u∥v,求x的值.

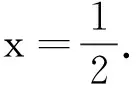
3.加强知识的网络性，奠定多样化解题基础

高中数学知识是一套成体系的结构，前后章节、内容之间均具有一定的逻辑关系，是知识的一种递进.并且在具体的数学解题过程中，同学们对知识的运用也必然是多样化的.亦即，在解决函数问题时并非只需要运用函数知识.这就要求同学们在学习高中数学的过程中需要构建起自己的知识结构体系，使其更加有章法、逻辑，以便在解答题目时运用自如.展开来讲就是，同学们在学习函数、进行习题练习过程中，可以将与其相关的知识联系起来，通过探究其内在逻辑，更为深入地理解数学知识，这样不仅有利于高效解题，也有助于同学们学会采用多种方法解答函数问题，创新思维方式.

总之，高中数学作为一门重要的学科，是很多同学在学习过程中的难点学科，尤其是在函数方面，其题目变化的多样性让很多同学的解题过程不够顺利，对基础知识的运用也不够灵活，思维存在一定的固化.在日常的学习和练习过程中，同学们通过对自身发散性思维、逆向思维以及知识体系的构建，能够为多样化解题奠定良好的基础，对于同学们函数解题能力的提升也具有重要的作用，而不是简单地学习个别解题步骤，思维的转变、方法的学习比学会解决个别题目更为重要.

参考文献：

[1]隋文哲.关于高中数学函数解题思路多元化的方法举例探索[J].学周刊,2017(05).

[2]李思雨.数学函数解题思路多元化初探[J].高中生学习(试题研究),2017(11).

[3]殷鹏展.关于高中数学函数解题思路多元化的方法举例研究[J].理科考试研究,2013(23).