明晰问题逻辑 优化展现素养

郑 良

(安徽省灵璧第一中学 234200)

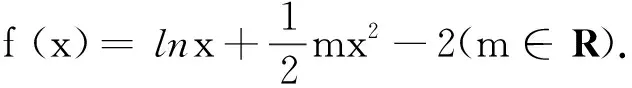
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线2x-y+3=0垂直，求实数m的值；

(2)若对任意x∈(0,+∞)，不等式f(x)+2≤mx2+(m-1)x-1成立，求整数m的最小值.

解(1)略.

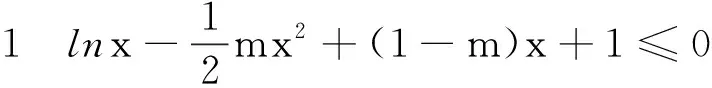
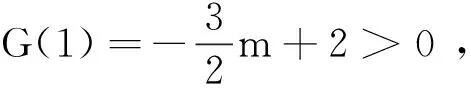
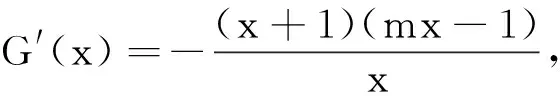
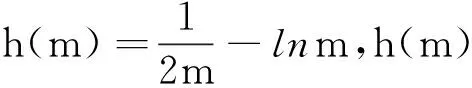
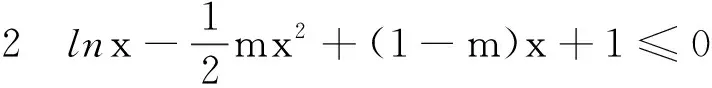
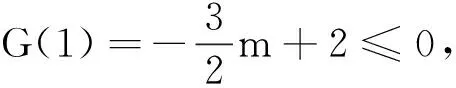
当m=2时,G(x)=lnx-x2-x+1≤x-1-x2-x+1=-x2<0，符合题意.

故整数m的最小值为2.

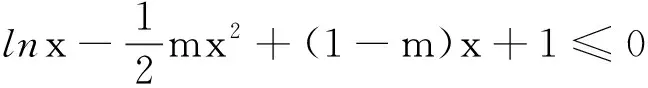
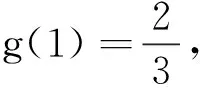
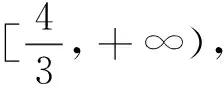
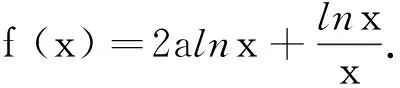
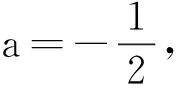
(2)若f(x)+2(x-1)≥0对任意的x∈[1,+∞)恒成立，求实数a的最小值.

解(1)略.

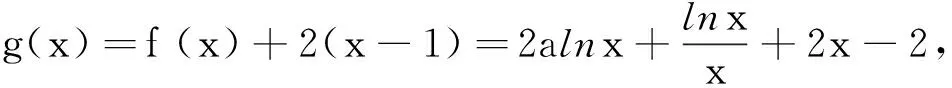
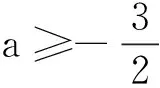
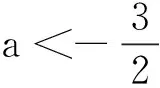
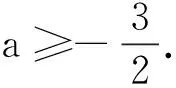
点评解法1为函数最值法，借助导数工具画出函数f(x)的图象.求导过程中遇到无法确定符号的部分，将其视为新函数，通过求导确定其性质，如此反复，直至确定最后一个函数导数的正负，再逆向追溯，逐步确定各原函数的单调性，在此过程可能涉及多次(级)讨论，过程烦琐.解法2抓住g(x)端点函数值g(1)为函数的边界值0，利用必要条件g′(1)≥0(对导函数使用必要条件)，只需对压缩后的参数范围进行求解，即验证结论的充分性.

参考文献：

[1]郑良，陈彬.整体认识自然优化本质揭示彰显素养[J].中学教研(数学)，2017(4)：4-10.