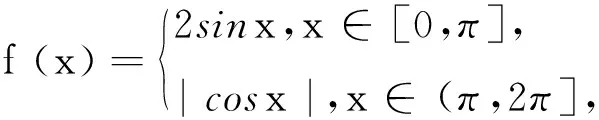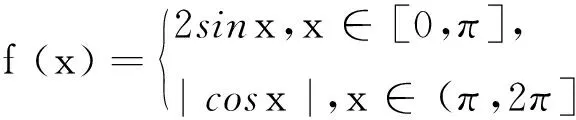高中数学选择题常用解法

陈安心

(湖北省洪湖市洪新小区 433200)

一、直接法

直接法是指从题干出发，直接进行推理计算并得出结论，然后将所得结果与题给选项比较选出正确的选项.直接法一般用在对定义的判断或直接计算能够很容易得出结论的问题上.

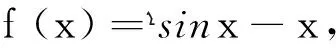
A.既是奇函数又是减函数

B.既是奇函数又是增函数

C.是增函数且有零点

D.是减函数且没有零点

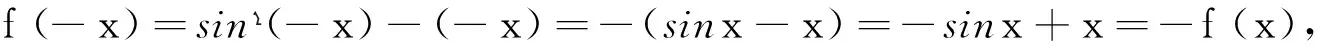
令f(x)=0，得sinx-x=0，解得：x=0,所以f(x)=sinx-x有零点x=0.

因为f′(x)=cosx-1≤0恒成立，所以f(x)=sinx-x是定义域上的减函数.即f(x)是奇函数、减函数且有零点,故选A.

点评本题考查函数的性质.根据函数性质的判断方法逐一直接判断即可，最后对照选项找出正确的选择支即为所要的结果.

二、代值法

因为选择题是提供题干及正确答案的问题，只是正确答案分散到四个选项中去了而已，因此，有时可以将选项代入题干进行判断是否符合，从而找出正确选项.代值法适用于选项特征明显或具有排他性的问题.

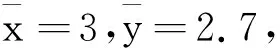
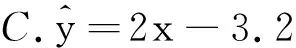
解析因为x与y负相关，所以排除B、C；又根据线性回归方程过样本点的中心，知线性回归方程过点(3，2.7)；将点(3,2.7)代入A、D中，只有A符合；故选A.

点评本题根据题干无法直接计算出答案，只能根据选项逐项代入求解.先根据线性回归方程的性质，x与y负相关，则线性回归方程中x的系数为负数；样本点的中心的坐标是样本平均数，而线性回归方程过样本点的中心.根据这些性质即可求解.

三、特值法

根据“选项中只有唯一一个正确答案”的思路，从题干出发，观察选项特征，取满足条件的特例(特殊点、特殊函数、特殊数列等)情况，根据其结果确定选项.

例3 函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )

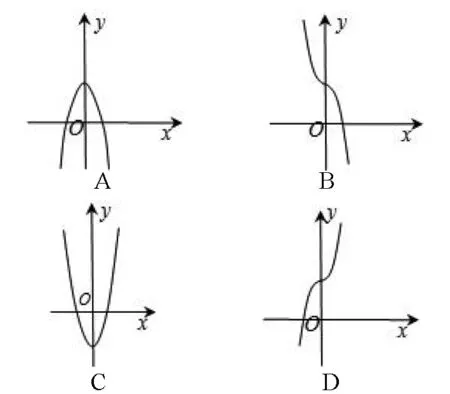
解析由f(-x)=4cos(-x)-e|-x|=4cosx-e|x|=f(x)得：f(x)=4cosx-e|x|是偶函数,其图象关于y轴对称，排除B、D.

当x=0时，y=4cos0-e0=4-1=3.

排除C,故选A.

点评本题直接根据题干给出的函数作出图象，再对应选项确定正确支几乎不可能.对于这类问题，我们通常利用特殊点的位置来排除错误项，最终得到正确的选项.

四、筛选法

有的问题难以直接判断选项的正误，但可以逐项筛选出正确(错误)项，从而最终得出的即是符合题目要求的选项.筛选法也称“排除法”.

例4 下列命题错误的是( )

A.若p∨q为假命题，则p∧q为假命题

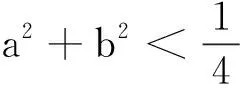
C.命题“∃x∈R使得x2+x+1<0”的否定是：“∀x∈R，x2+x+1≥0”

D.已知函数f(x)可导，则“f′(x0)=0”是“x0是函数f(x)极值点”的充要条件

解析若p∨q为假命题，则p假且q假，所以p∧q为假命题.A正确.

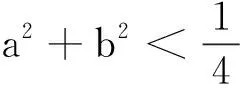
因为“∃x∈R使得x2+x+1<0”的否定为“∀x∈R，x2+x+1≥0”,C正确.

对于函数f(x)=x3,有f′(x)=3x2,取x0=0,则有f′(x0)=f′(0)=0,但x0=0不是函数f(x)=x3的极值点,D错误,故选D.

点评本题给出四个选项分别考查不同的知识点，因此要最终得出正确的选项，必须逐项进行判断，最终筛选出正确的选择支.

五、分析法

根据给出的四个选项，分析它们之间的逻辑关系，寻找出可能的答案；也可以将题干与选项当作一个整体，寻找它们之间的共同特征，根据这些特征，从而分析出正确选项.

例5 (合肥市2016年高三第三次教学质量检测)若函数f(x)=2x+x-2016的一个零点x0∈(n,n+1)，则正整数n=( )

A.11 B.10 C.9 D.8

解析因为f(x)=2x+x-2016的一个零点x0∈(n,n+1)，

而210=1024,211=2048,所以f(10)=210+10-2016=1024+10-2016<0,

f(11)=211+11-2016=2048+11-2016>0,

f(10)·f(11)<0.

所以f(x)在(10，11)上有零点,即n=10.故选B.

点评本题考查函数的零点的计算，给出选项中最大的数n为11，根据幂函数2x的不同取值分析可知n取10时最合适，经验算从而最终选出结果.

六、估算法

在直接计算难度较大时，可以根据题干信息，先估算出结果的大致范围，再排出错误的选项，从而得出正确的结果.

例6 (唐山市2015～2016高三年级第二次模拟考试)已知a=log34,b=logπ3,c=50.5,则a，b，c的大小关系是( )

A.a

C.b

解析对于a=log34，而1=log33

又b=logπ3

所以b

点评对于这类指数、对数判断大小问题，一类情况是两两之间直接比较大小，另一种就是找一个中间量来帮助比较大小，常见的中间量如0，1，2等.如本题就是找一个中间量估计对应值的大小，从而判断出大小关系.

七、数形结合法

对有的数学问题，直接计算难度较大，但利用图形能直观简单计算出结果时，通常考虑数形结合，通过图象帮助解题.

A.(0，1) B.[1，2]

C.(0，1] D.(1，2)

点评本题考查三角函数的性质与函数图象的应用.直接计算很难得出结论，但利用数形结合法则可快速观察出点的位置，从而得出结果.

总之，选择题是高中数学中的一类重要题型，题量大，分值高.对于大多数的问题，我们需要利用常规方法直接计算出结论，但对于有些问题则可以灵活运用上述方法来简便运算，从而节约解题时间，取得更高的分数.

参考文献：

[1]王鹍,陈安心.高考数学选择题快速突破技巧[J].学子,2003(01).