圆柱平底螺旋立铣刀动态切削力仿真与应用*

葛任鹏 仇 健 韩廷超 李 帅

(沈阳机床(集团)有限责任公司高档数控机床国家重点实验室，辽宁 沈阳 110142)

铝合金具有密度低、比强度高、比刚度高、导热性和导电性好、工艺性和耐腐蚀性好等一系列优点，是航空领域重要的结构材料[1]。但由于其刚性较差，而且航空领域中大量使用薄壁结构材料，使得铝合金在加工过程中易于变形，严重影响加工精度，而切削力是影响加工变形的重要因素，因此在铝合金的加工过程中对切削力的控制和预测显得格外重要。

7075铝合金是航空领域中应用的重要铝合金材料之一，进行7075铝合金切削加工切削力建模对切削力的预测和变形控制具有重要意义。目前，国产数控机床或加工中心用刀具在切削性能、耐用度等方面与国外同类产品相比有一定差距，其原因除刀具材料外，刀具设计理论方面的研究也非常重要。以数控铣削加工中广泛应用的平底螺旋立铣刀为例，在国内外研究基础上，建立螺旋立铣刀的动态切削力模型[2-8]，为切削力的预报、仿真及加工过程中工艺参数的优化提供理论依据。

1 铣削加工动态铣削力建模

根据瞬时刚性力模型，作用在刀齿j上第k个切削刃微元上的切向力、径向力和轴向力微元可以表示为

(1)

式中：Ktc、Krc、Kac为切向、径向和轴向切削力系数；Kte、Kre、Kae为切向、径向和轴向刃口力系数；dFtj、dFrj、dFaj为微元切削刃切向、径向和轴向切削力；dz为切削宽度微元；ds为切削刃微元接触长度微元；g(θj)为单位阶跃函数，用来表示当前刀齿是否参与切削；h(θj(z)) 为瞬时切削厚度。

(2)

式中:θst为切入角；θex为切出角。

h(qj(z))=fzsin(qj(z))

(3)

式中：fz为每齿进给量。

假设圆柱立铣刀螺旋角为β、直径为D，将圆柱立铣刀沿轴向进行离散，螺旋角使得径向接触角沿轴线由齿底向上递减。刀齿j在轴向z处的接触角为：

θj(z)=θ+(j-1)θp-kβz

(4)

式中：j=1，2，…，N，其中N为齿数；z为切削刃微元距刀齿底部距离；θj(z)表示第j个刀齿在高度为z处微元的接触角；θ为序号为1的刀齿底部接触角；θp=2π/N为齿间角(假设刀齿均匀分布)。在轴向切深z处滞后角φ为：

(5)

式中，kβ=2tan(β)/D;β为铣刀螺旋角;D为铣刀直径;z为切削刃微元距刀齿底部距离。

在实际加工过程中，通过测力仪可以很容易得到的是机床坐标下的X、Y和Z三个方向上的铣削力，因此为了得到机床坐标下的X、Y和Z三个方向的铣削力，必须首先通过坐标变换获得刀具坐标下的X、Y和Z三个方向上的铣削力，如下：

(6)

对每个切削刃上各个切削刃微元的作用力进行求和即可得到该切削刃上的铣削力，将各个切削刃上的铣削力求和之后，可得到该铣刀在进给方向、法线方向以及轴线方向上的瞬时切削力，将微元切削力代入上式并对参与切削的部分进行积分得：

(7)

要计算切削力，必须求出积分上下限。根据刀齿j和每个刀齿的接触角，求轴向积分限分下列5种情况(情况2与情况3互斥)，如图2所示。

(1)如果θj(z=ap)<θst<θj(z=0)<θex(第j个刀齿的底部处于切削过程中，最大切深处尚未切入)，则：下限θj,1=θj(z=0)，上限θj,2=θst。

(2)如果θst<θj(z=ap)<θj(z=0)<θex(第j个刀齿的全部处于切削过程中)，则：下限θj,1=θj(z=0)，上限θj,2=θj(z=ap)。

(3)如果θj(z=ap)<θst且θj(z=0)>θex(第j个刀齿的底部已切出，最大切深处尚未切入)，则：下限θj,1=θex，上限θj,2=θst。

(4)如果θj(z=ap)<θst<θex<θj(z=0)(第j个刀齿的最大切深处于切削过程中，底部已切出)，则：下限θj,1=θex，上限θj,2=θj(z=ap)。

(5)如果θex<θj(z=ap)<θj(z=0)(第j个刀齿的全不处于切削过程中)，则：作用于该上的切削力为0。

通过将上述办法求得的积分限代入到式(7)中，便可求得各个瞬时的作用力。将每个切削刃的作用力求和便得到铣刀受到的瞬时合力：

(8)

为了避免刀具偏心的影响，通常采用平均切削力进行计算。由于一个齿周期内每个刀齿切除的材料总量是一定的，与螺旋角无关，所以可以假定铣刀螺旋角为0，计算平均切削力如式(9)所示。

(9)

式中：N为铣刀齿数；a为轴向切深；fz为每齿进给量。

2 铣削力系数辨识

全齿铣削(槽铣)试验最为简单，将切入角θst=0，切出角θex=π，代入式(9)得：

(10)

通过切削试验测得不同进给量下平均切削力，利用线性回归分析方法拟合平均切削力与每齿进给量之间的线性方程式：

(11)

对比式(10)、(11)，可得：

(12)

由式(12)可知径向切削力系数(Krc、Kre)由进给方向平均切削力决定，而切向切削力系数(Ktc、Kte)由切削平面内垂直于进给方向的平均切削力决定，轴向切削力系数(Kac、Kae)由轴向切削力平均值决定。

对切削力模型进行验证，在卧式加工中心HMC63上进行7075铝合金铣削加工切削力系数辨识试验，试验条件如表1所示。

表1 试验条件

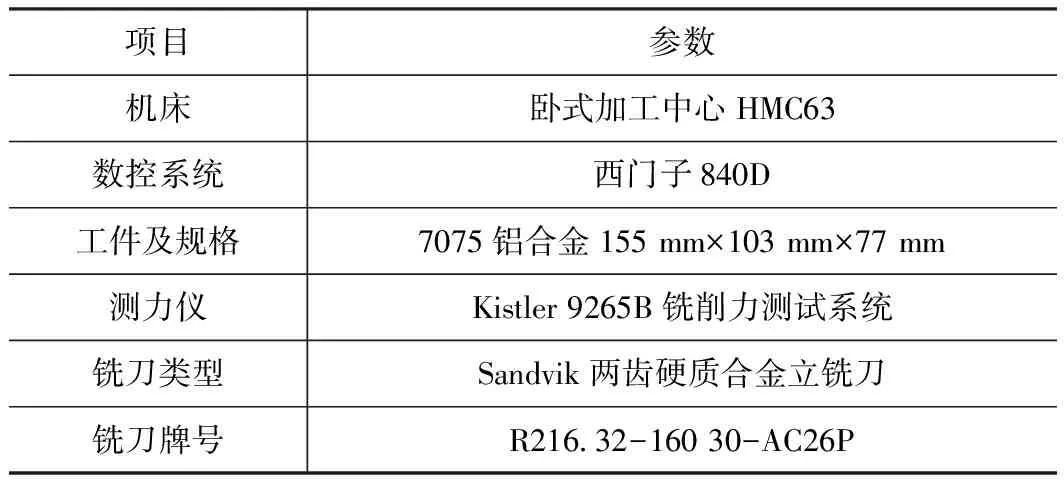
项目参数机床卧式加工中心HMC63数控系统西门子840D工件及规格7075铝合金155 mm×103 mm×77 mm测力仪Kistler 9265B铣削力测试系统铣刀类型Sandvik两齿硬质合金立铣刀铣刀牌号R216.32-160 30-AC26P

试验现场如图3所示。

保持转速、切深和切宽不变，通过改变每齿进给量进行7075铝合金切削力测试试验，取测得的切削力平均值作为实验结果，试验参数及实验结果如表2和表3所示。

表2 试验参数

主轴转速n/(r/min)切深ap/mm切宽ae/mm每齿进给量fz/(mm/齿)5 0002160.03、0.06、0.09、0.12、0.15

表3 试验结果

每齿进给量fz/(mm/齿)Fx/NFy/NFz/N0.0319.9412.6120.580.0633.0316.3823.560.0941.3519.3424.350.1250.7122.3426.810.1572.7526.4227.94

将线性回归方程式中的系数代入式(12)中得到切削力系数如表4所示。

表4 切削力系数

切削力系数/(N/mm2)刃口力系数/(N/mm)KrcKtcKacKreKteKae-411.00111.9347.05-5.167.349.63

3 动态铣削力仿真及验证

利用MATLAB软件编制程序进行圆柱平底螺旋立铣刀瞬时切削力数值仿真，程序流程图如图5所示。

为了验证模型的可靠性及切削力系数辨识的准确性，有必要进行切削力测试验证试验。图6为按照主轴转速5 000 r/min，切深2 mm，切宽16 mm，每齿进给量0.1 mm/齿参数进行实际切削获得的切削力波形与切削力数值仿真结果的对比效果。由仿真结果和实测波形对比，可知：各方向切削力的仿真结果的变化趋势同实测结果的变化趋势相同；实测曲线与仿真曲线的数值十分接近；各方向切削力之间的相位关系的实测曲线与仿真曲线一致，说明切削力仿真正确有效，可以准确地预测切削力。

4 实际应用

通过上述模型的建立和试验验证，说明模型准确，可以用来进行切削力的预测。应用在切削力的预测和无传感器切削力监测两个主要方面。

(1)用户不需要实际切削，利用该模型即可得到不同参数下切削力的预测结果，即可以用来进行瞬时切削力的预测。按照表5中的参数输入该仿真模型中进行瞬时切削力仿真。

表5 仿真参数

参数编号转速n/(r/min)切深ap/mm切宽ae/mm进给fz/(mm/齿)15 0002160.425 0002160.235 0004160.245 0004120.2

切削力仿真结果如图7所示。

(2)用户可以实现无传感器监测实际工件铣削时的切削力。通过提取实际加工G代码中的切削用量，根据切削用量利用该模型实现切削过程切削力实时监测，即实现瞬时切削力的无传感器监测。

5 结语

(1)建立了平底螺旋立铣刀铣削动态切削力模型，

根据切削力测试试验建立了切削力系数与切削参数之间的关系模型，实现对铣削过程中切削力的预测，7075铝合金铣削试验对所建立的动态切削力模型的验证结果表明所建立的动态切削力模型能够较准确地预测切削过程中切削力。

(2)对7075铝合金铣削时切削力进行预测、控制，实现切削力预测和无传感器切削力监测，进而用于进行薄壁工件加工时加工变型控制。

(3)切削力系数的获取可以进一步进行切削稳定性分析，提高航空结构件的加工精度和效率。

[1]杨守杰, 戴圣龙. 航空铝合金的发展回顾与展望[J]. 材料导报, 2005, 19(2):76-80.

[2]Yun W S, Cho D W. Accurate 3-D cutting force prediction using cutting condition independent coefficients in end milling[J]. International Journal of Machine Tools & Manufacture, 2001, 41(4):463-478.

[3]中国科学技术协会. 第十五届中国科协年会论文集[C]. 贵阳:[出版者不详]，2013:1-5.

[4]Engin S, Altintas Y. Mechanics and dynamics of general milling cutters.: Part II: inserted cutters[J]. International Journal of Machine Tools & Manufacture, 2001, 41(15):2213-2231.

[5]刘璨, 吴敬权, 刘焕牢,等. 平底立铣刀在多刃切削时的切削力变化规律研究[J]. 中国机械工程, 2016, 27(10):1352-1357.

[6]Wang M H, Gao L, Zheng Y H. An examination of the fundamental mechanics of cutting force coefficients[J]. International Journal of Machine Tools & Manufacture, 2014, 78(1):1-7.

[7]杨毅青, 张斌, 刘强. 铣削建模中多种切削力模型的分析比较[J]. 振动工程学报, 2015, 28(1):82-90.

[8]Ozturk E, Ozkirimli O, Gibbons T, et al.Prediction of effect of helix angle on cutting force coefficients for design of new tools[J]. CIRP Annals - Manufacturing Technology, 2016, 65(1):125-128.