浅谈数学解题能力的提高
高 东
(黑龙江省兴隆林业局高级中学 151801)
一、审题
审题是解题的基础,审题不仅是要一字不漏的读题,而且要分清已知什么,特别是有哪些隐含条件及限制条件,要仔细观察,反复思考,深入分析,展开联想,在审题时,要特别注意以下几个问题.
1. 由表及里,深挖隐含
每道题目皆有条件和结论,审题时要逐句地看,既看清已知条件,又看清结论,更不能忘记考虑隐含条件.
2.仔细分析,理解含意
有些问题不易一看就明,尤其是应用题,此时对于关键的字、词、句须仔细分析,理解含意,探明解题思路.
3.找准关键,全力突破
审题时,需要研究每个条件的作用,探明主要矛盾,找准关键,然后全力突破,实现一通皆通.
二、解题表述
现在是信息时代,信息量较大,大多数学生在解题时,常常只注重思维的过程,对书面表述不够重视,从而导致“对而不全”.为了提高解题的正确率,在解题教学中既要重视解题思维的培养,又要重视书面表述,使之做到解题步骤完整,逻辑推理严谨,书写格式规范,结论正确完整.
例2 已知命题P:函数g(x)的图象与函数f(x)=1-3x的图象关于y=x对称,且|g(a)|<2;命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0},且A∩B=Ø,求实数a的取值范围,使命题P与Q有且只有一个为真命题.
审题本题需要解决以下几个问题:①g(x)=?;②P真时,a的范围?③Q真时,a的范围?④命题P与Q有且只有一个为真命题时,P、Q的真假性如何?
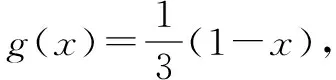
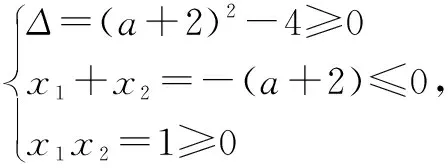
∴-4
∵命题P与Q有且只有一个为真命题,

∴-5
此题虽是一道较为综合的题目,但只要仔细审题,明确目标,按步就班,一步一个脚印的表述出来,就会得到较为满意的分数.
三、反思
美国当代最著名的数学家G·波利在他的最著名的解题著作《怎样解题》中,把解题分成四个阶段:理解题目、拟定方案、执行方案、回顾反思.可见回顾反思的重要性.教学实践告诉我们,在解题教学中,并不在于讲解了多少遍例题,而在于学生真正掌握了多少,有没有形成能力.解完数学题后,如果能够回顾一下解题过程,并作进一步探究,不仅能巩固已学过的知识,,避免解题的错误,更重要的是还能掌握解题技巧,提高能力,教学实践证明,这样做常常可以收到事半功倍的效果.
1.反思过程,发现错误
解题是掌握基本知识,发展思维能力,形成基本技能的重要环节,因此,解题后对习题进行不同程度的再反思,以便发现新的问题和可能产生的错误及其原因,这是解题后不可缺少的环节.
2.反思方法,找出最优
在解题过程中,不能仅满足于做题、做得正确,还应在解题后去再思考,找出解题中更优的方法和技巧.
3.反思题变,触类旁通
选择一个题目,可使学生将所学知识纵向加深,横向沟通,提高分析问题和解决问题的能力.
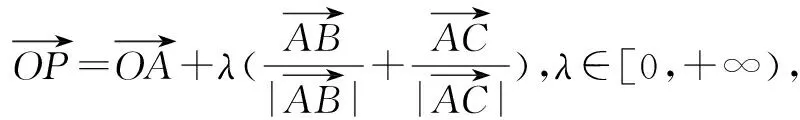
在解好此题后,为了收到更大的效益,可将原题作如下变式,要求学生解答:
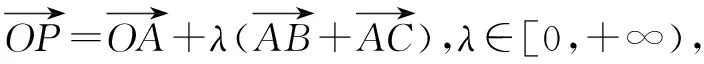


通过上述变题,可使学生对向量共线的充要条件有更进一步的认识和理解,对三角形的四心有更深刻的认识.
综上所述,只要我们在数学学习中重视解题的“三步曲”——审题、解题表述、反思,就能使数学解题能力不断提高.
参考文献:
[1]伍俊溢,廖俊淇.高中数学“一题多解”的学习心得[J].考试周刊,2016(78).

