基于应用能力提高的概率论案例教学法的研究与实践
梁 瑛,吴宏锷
(南阳理工学院,河南 南阳 473004)
随着地方本科高校转型的发展,教学改革也势在必行.数学的教学已经不单单是数学理论的学习,而应该以应用为目的,突出思想性,强调应用性,重点放在培养学生应用数学的意识和应用数学知识解决实际问题的能力这个目标上.要实现这个目标,案例教学法就显得非常重要.概率论是数学的一个有特色且又十分活跃的分支,该课程应用性强,许多专业都会用到.概率论与我们生活息息相关,可以说许多定义概念都源于生活又服务于生活.根据多年的教学实践,发现在概率论课程的教学中运用案例教学法对于培养学生学习的兴趣、提高学生学习的积极性、提高学生的应用能力和创新意识有着很大的促进作用.
1 案例的实施
传统的数学教学,教师更多地偏重于概率论课程理论的严密性、逻辑性、完整性,局限于所使用的教材,缺乏一些相应知识点的案例联系和应用案例,对它在实际生活中的应用重视不够,使得概率论的教学效果不是很理想,概率论与其它数学分支不同的是概率论的产生与发展完全源自生活[1].可以说问题的出现和解决促进了概率论的发展,因此实际问题是概率论的源头,又是概率论的归宿.通过案例教学法,不仅能加强相关的理论、方法与思想的可视性,使学生掌握概率论基本理论的来源,而且可以培养和提高学生运用概率论的原理和方法解决实际问题的能力.在概率论的课堂中改变以往数学教学以理论计算为重的方式,利用案例教学法,提高教学内容的使用性,可以增强概率论教学的效果,有助于教学目标的实现.实施案例教学在教学方法和教学手段上应该配套,主要采用“三融入“和”一结合“的教学方法和手段来实现.
1.1 案例在基本理论引入时的融入
在教学中应尽可能地把基本概念和方法回归到实际背景,这样可以加强理论的可视性,有助于激发学生学习兴趣和提高学生应用能力.如可通过生活中常见的转盘抽奖案例来引入几何概型.(案例1).
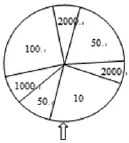
案例1 在彩票开奖的现场有一个互动节目,其规则是抽取一名幸运观众,上台随机转一下右图所示的转盘,转盘停下时,指针会指向一个标着某数字的扇形,这个数字就是该参与者当场可得到的奖金(单位:元).若转盘的周长是,两个标着“2000”的扇形的弧长分别为a和b,那么该幸运观众能得到2000元奖金的可能性是多少呢?[2]
上述随机试验的所有可能结果,一是指针指向转盘圆周上的某个点(有无数个);二是指向每个点的可能性相等,具有这两个特点的随机试验即为几何概型.通过分析该试验的特点,引出几何概型的定义.本例中该幸运观众能得到2000元奖金的可能性是P(指针指向标有“2000”扇形)=a+b/L.进而自然而然地给出几何概型的概率计算公式.一般地,设几何概型样本空间对应的几何区域为Ω,事件A对应Ω 的一个子区域,则有 P(A)=m(A)/m(Ω).其中 m(A)、m(Ω)表示样本空间Ω和事件A对应的几何测度.
再如,在讲随机变量的数学期望概念时,可先引入历史上著名的分赌注案例(案例2).
案例2 十七世纪中叶,赌徒梅尔向法国数学家帕斯卡提出一个使他苦恼已久的分赌本问题:他和保罗两人掷硬币赌钱,事先每人各拿出6枚金币.约定先胜三局者便赢得全部金币.比赛进行到保罗胜一局,梅尔胜两局时中断了赌局.他们商量分配这12枚金币,保罗认为,根据已胜的局数,他应得总数的三分之一,即4枚金币,梅尔应得总数的三分之二,即8枚金币.但梅尔认为这样分他有点“亏”,那么到底怎样分才合理呢?
在给出这样案例后,学生十分感兴趣,课堂气氛很活跃,学生众说纷纭.教师可引导学生思考分析.设想再赌下去,梅尔最终所得金币是一个随机变量X,可能取值为0、12.再赌两局必可结束.对于梅尔来说可能出现的结果有以下四种:(胜,胜),(胜,负),(负,胜),(负,负).其中前有三种情形有利于梅尔得到12枚金币,故梅尔所得金币X的分布律为

由上述分析,梅尔期望所得金币为0×1/4+12×3/4=9枚,于是保罗应分得3枚金币.这种分法的合理之处在于不但考虑了已赌局数,而且也包含了对再赌下去的一种“期望”,由此案例给出离散型随机变量数学期望的定义,这样使学生明白随机变量的数学期望实质内涵.通过该案例的引入,使学生在愉快的学习氛围中了解到概率论的起源和期望概念的来由,同时也加深了对数学期望概念的理解,更为重要的是掌握了利用期望解决生活中类似问题的方法.
在概率论的教学中,选取合适的生活案例或者概率论发展史上典型案例融入相关理论的教学中,有助于增强概念的可视性与应用性,有利于教学目标的完成.
1.2 案例在理论知识应用中的融入
在概率论的学习过程中为加强理论的应用,在讲完理论后,教师应引导学生运用所学的概率论知识来解决实际问题.如利用相关的知识解释生活中俗语谚语、解释身边的事物或热点问题.比如在学习概率性质以及事件的独立时,可让学生解释生活中的一些谚语俗语,如“常在河边走,哪能不湿鞋?”“三个臭皮匠,抵个诸葛亮”“先下手为强,后下手遭殃”等等.虽然有些谚语不是绝对正确的,但其中也包含了朴素的唯物论,具有一定的合理性.
案例3 某油田指挥部要选择在A区域或B区域试钻一口油井,A区域油井钻探费为60万元,出油概率为0.3,若出油则有1000万元的收入;B区域油井钻探费为20万元,出油概率为0.8,若出油则有200万元的收入.指挥部将如何进行决策?[3]
实施案例教学多采用讲授和讨论相结合的教学方式,讨论为主,讲授为辅,逐步引导学生掌握解决问题的方法.通过对案例的讨论解决,学生可以体验使用所学知识解决实际问题的全过程,进一步增强他们的学习兴趣和提高应用能力.实践表明这种教学方法能真正达到“学以致用”的目的.
1.3 案例在课下练习中的融入
针对概率论知识实用性强的特点,可以精心选择一些代表性强的综合案例.以丰富的网络为资源,引导学生自学,3-5人为一组,让学生课下分成小组完成.通过这种方式不但可以检验学生知识掌握的程度以及实际应用的能力,并且还可以培养学生查阅文献、团队合作、写作表达和勇于创新的能力,为参加全国大学生数学建模竞赛奠定基础.该项练习可以纳入平时成绩的考核中.如随机变量数字特征的综合应用案例(案例4).
案例4 万德隆超市进行有奖销售,投放100张奖券,其中只有一张有奖,问:
(1)第一个人中奖的概率是多少?
(2)第二个人、第三个人中奖的概率是多少?
(3)第k(1≤k≤100)个人中奖的概率呢?中奖的概率与k是否有关,即中奖的概率与抽取的次序是否有关?
(4)若其中2张有奖,则第k(1≤k≤100)个人中奖的概率是多少?若n张奖券,其中m张有奖,则每位顾客中奖的概率是多少?
该教学案例设计时为了突出教学的重点,抽象数字可先设计为具体数字,先计算第一个人中奖的概率,然后在计算第二个人、第三个人、第k(1≤k≤100)个人中奖的概率.该案例的设计紧扣教学内容,又体现了循序渐进的思想.最终启发学生得到,中奖的概率仅与奖券所含的比例有关.
在教学的过程中会发现学生对于第一个人中奖的概率会很快地算出,而在计算第二个人中奖的概率往往考虑到第一个人可能中奖,也可能没有中奖.基于这种思想,正是后面全概率公式解决的方法,因此在后面可用全概率公式讲解.
2 案例实施的注意事项
编写案例要难易程度适中,难点要分散.在教学过程中,对课程的教学内容以及知识点应有整体的把握,对要实施案例教学的内容有一个统筹的规划,课堂案例不能设计的太难,否则课堂无法完成,还会给学生平添一种不知所云的感觉,教学效果可想而知.而课下案例作业可设计一些综合性的案例,让学生课下查阅资料完成,以拓宽学生的视野,提高学生解决实际问题的能力.
3 课程考核评价指标多元化
根据概率论课程的特点,课程成绩考核可加大过程考核.平时考核中注重检验学生应用能力和创新能力的形成,注重考核学生撰写的学习心得或小论文.课程期末总评成绩,采用将平时成绩(30%)和考试相结合(70%)的方式.平时成绩主要包括考勤、课后习题作业、课外案例作业、小测验等评价指标,如设置出勤及课堂讨论占40%,课后习题作业、单元测试占30%,课外案例作业占30%.课外作业按小组进行,老师给出成绩后,再依据每组组长给出的组成员做题时贡献大小作为权重算出每个学生的得分.这种方式不仅可以促进团队合作、交流,而且可以督促学生从多个角度、多个方面去分析问题和解决问题的.
课程考核评价指标的多元化可以引导学生从注重“考试结果”向注重“学习过程”转变,对于调动学生学习的积极主动性,培养学生良好学习习惯,培养学生的创新意识,提高学生的实践能力有重要的意义.这种评价模式使得评价结果更客观、更全面.
鉴于概率论课程的特点,采用案例教学可以使学生更好地理解概念、公式以及掌握它们的应用.本文对概率论教学过程中案例如何实施以及实施时的注意事项进行了探索研究.实践表明案例教学法对于提高学生学习的积极性,提高学生的应用能力和培养学生的创新意识大有裨益.
〔1〕 梁瑛,吴宏锷.转型背景下《概率论与数理统计》教学的改革与实现[J].高教学刊,2016(21):160—163.
〔2〕 马戈.概率论与数理统计[M].科学出版社,2012.
〔3〕 唐国兴.概率统计[M].武汉大学出版社,1991.

