动力用煤的各粒级原料煤及选煤产品密度与灰分关系研究

梁 辽，刘 涛，高 美，吴大为

(1.北京国华科技集团有限公司，北京 101300；2.唐山国华科技国际工程有限公司，河北 唐山 063020)

在选煤厂工程设计中，受煤、贮煤、卸煤、输煤设备和设施能力的确定，都需要以煤炭松散密度(堆密度)作为基础数据；而此数据源于煤炭生产数据，尤其是动力煤选煤厂，要生产多粒级不同质量的产品，方能得到其密度数据。

煤炭的密度与煤岩类型、煤化程度及煤中矿物质成分和含量密切相关[1-2]。原料煤的密度与灰分具有正相关关系[3-4]，但有关各粒级煤炭产品是否也遵循上述规律，经文献检索，有关这方面的研究较少。笔者借助于选煤厂重力选煤设备单机检测资料，探讨各粒级选煤产品的密度与灰分的关系。

1 原始资料

在淮南矿业集团谢桥矿选煤厂的《大直径无压给料三产品重介质旋流器在动力煤选煤厂的应用研究》[5-6]科研报告中，提供了该厂所使用的3GHMC1400/1000AP型重介质旋流器单机检测的原料煤、精煤、中煤和矸石各5个粒级的密度组成数据[7-8]，这些资料不但是严格按照GB/T 15715—2014《煤用重选设备工艺性能评定方法》[9]进行的，而且还在以下方面提高了分析研究的精确程度。

(1)对原料煤及选煤产品不是通过通常的7个密度级[10]进行浮沉试验，而是分为9个密度级。

(2)1.60～1.90 kg/L密度级之间，以窄密度级0.05 kg/L来划分区间，而不是常规的以宽密度级0.10 kg/L来划分区间[11]。

(3)采用专门的无机重液，把浮沉试验的最高密度级由2.00 kg/L提高到2.10 kg/L。

(4)按GB/T 15715—2014《煤用重选设备工艺性能评定方法》要求进行重介质旋流器单机检测，检验结果均方差为0.45，小于临界值1.40，故引用的资料有效、可信，也表明选煤设备中原料煤的各密度级物料有规律地分配到选煤产品中。各粒级原料煤及选煤产品的密度与灰分关系见表1。

表1 各粒级原料煤及选煤产品的密度与灰分关系

从表1可以看出：①各粒级的选煤产品和原料煤一样，灰分随着密度的增高而增高；②无论是各粒级的选煤产品还是原料煤，同一密度级的灰分是比较接近的，灰分高低的波动是随机的，这种随机性是因煤炭本身就是散状不均质可燃固体矿物，在选煤设备单机检测的采样、筛分、浮沉试验、制样和化验的全过程中随机误差也不可避免；③由于重介质旋流器分选精度高，在精煤和中煤的50～25、25～13 mm粒级中>1.80 kg/L密度级产率极少，甚至为零。在矸石的50～25、25～13 mm粒级中<1.80 kg/L密度级产率也极少，几乎为零。这些数量极少的试样所得到的化验结果可能出现较大的误差。

2 各粒级原料煤和选煤产品的密度与灰分关系

在煤炭行业，一般将煤炭中的1.80 kg/L密度作为分界点。<1.80 kg/L密度级视为煤，以可燃体为主要成分；>1.80 kg/L密度级视为矸石，以非可燃体为主要成分。两者的密度与灰分的关系可能有所区别，为此首先将各粒级原料煤和产品分别按<1.80 kg/L密度级和>1.80 kg/L密度级来探讨它们之间的密度和灰分的关系[12-13]。

根据表1所列原始数据，将原料煤中的50～25 mm粒级的1.60～1.80 kg/L密度级的平均密度与灰分之间的关系进行推导，结果见表2。

表2 50～25 mm粒级原料煤中1.60～1.80 kg/L密度级的密度与灰分相关关系

δ=1.186+0.011 9A，

(1)

式中：δ为平均密度，kg/L；A为灰分，%。

由式(1)可知，当煤炭灰分每增高10个百分点时，它的密度相应提高0.12 kg/L。式(1)也可以写为：

A=84.03δ-99.66，

(2)

从式(2)得出：煤炭密度每增高0.01 kg/L时，其灰分相应提高0.84个百分点。

相关系数为

(3)

在自由度φ=4-2=2，查表取α=0.01时，γ0.01=0.990[14]，由式(3)中γ=0.998，即γ>γ0.01，说明密度在1.60～1.80 kg/L范围内的50～25 mm粒级原料煤中密度与灰分之间存在良好的正相关关系，在α=0.01的水平上是显著的，所获得回归方程有99%的可靠性[12]。

用同样的步骤推导了各粒级原料煤和选煤产品的<1.80 kg/L和>1.80 kg/L密度级的密度与灰分的回归方程(表3)。

表3 各粒级煤炭的回归方程

从理论上讲，应该建立起<1.80 kg/L密度级和>1.80 kg/L密度级各20个回归方程。但实际情况是重介质旋流器分选精度高，50～25 mm粒级精煤中不存在>1.65 kg/L密度级产物；50～25 mm和25～13 mm粒级中2.00～2.10 kg/L密度级煤的产率为零或接近于零；50～25 mm和25～13 mm粒级中<1.80 kg/L密度级的矸石产率为零，所以只建立了<1.80 kg/L和>1.80 kg/L密度级各17个回归方程。

上述回归方程可靠性较高，除一个为90%外，其余都在95%以上，有的甚至达到99.9%。说明各粒级选煤产品与原料煤一样，存在密度与灰分良好的正相关关系。

将50～25 mm粒级原料煤中1.60～1.80 kg/L的煤炭和1.80～2.10 kg/L的矸石两条回归方程线绘于图1。从图1中可看出，<1.80 kg/L密度级的回归线截距略大些，斜率稍小些。它们是延长相交的斜直线，其交点可由作图法确定，或由二者的回归方程求得。

图1 50～25 mm粒级原料煤中煤炭和矸石的密度与灰分的回归方程线

1.60～1.80 kg/L密度级的回归方程为δ1=1.186+0.012A1，1.80～2.10 kg/L密度级的回归方程为δ2=0.989+0.016A2，在坐标系中，满足交点的条件是δ1=δ2，A1=A2，则1.186+0.012A=0.989+0.016A，可得δ=1.78 kg/L，A=49.25%。而且每个粒级煤炭的两条回归方程线都存在这一现象，即<1.80 kg/L密度级的截距比>1.80 kg/L密度级的截距稍大些。而斜率则相反，<1.80 kg/L密度级比>1.80 kg/L密度级的略小，因此两条回归线均有交点。

<1.80 kg/L密度级的各粒级原料煤和选煤产品回归方程线的截距平均值为1.201，斜率平均值为0.012，且数据较为集中；>1.80 kg/L密度级的各粒级原料煤和选煤产品回归方程线的截距平均值为1.029，斜率平均值为0.016，但数据的集中程度比前者差一些，这可能是>1.80 kg/L密度级灰分高所造成的。

3 50～0.5 mm综合粒级原料煤和选煤产品的密度与灰分关系

3.1 50～0.5 mm综合粒级中<1.80 kg/L密度级和>1.80 kg/L密度级的密度与灰分关系

从表3中发现，无论是原料煤还是选煤产品，在各自粒级的<1.80 kg/L和>1.80 kg/L密度级回归方程中，截距a值和斜率b值彼此是极接近的，它们的差别多数为小数点后第三位。

鉴于此情况，笔者又引用该厂的单机检查资料中50～0.5 mm综合粒级原料煤和选煤产品密度组成数据(表4)推导出相应的回归方程(表5)。此处的50～0.5 mm综合粒级灰分，不是各粒级灰分的算术平均值，而是根据各粒级的产率，用加权平均方法计算出来的灰分值[15]。

表4 50～0.5 mm各粒级密度与灰分关系对照

表5 50～0.5 mm综合粒级的回归方程

将50～0.5 mm综合粒级原料煤和选煤产品各自的1.60～1.80 kg/L密度级煤炭和1.80～2.10 kg/L密度级矸石两条回归方程线分别绘于图2—图5。

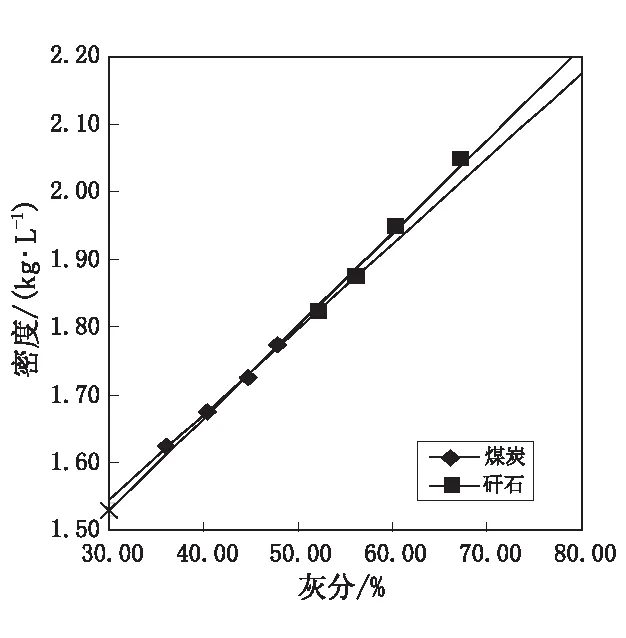
图2 50～0.5 mm综合粒级原料煤中煤炭和矸石的密度与灰分回归方程线

图3 50～0.5 mm综合粒级精煤中煤炭和矸石的密度与灰分回归方程线

图4 50～0.5 mm综合粒级中煤中煤炭和矸石的密度与灰分回归方程线

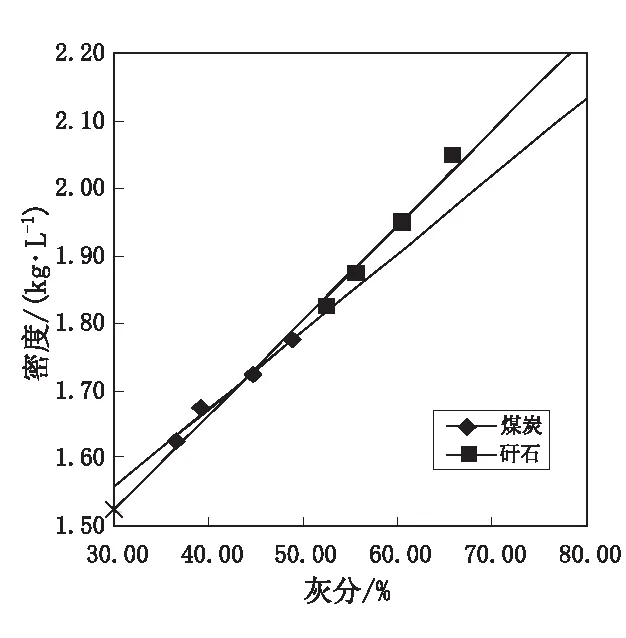
图5 50～0.5 mm综合粒级矸石中煤炭和矸石的密度与灰分回归方程线

从图2—图5可以看出：①它们的回归方程线均有交点，<1.80 kg/L密度级的截距比>1.80 kg/L密度级稍大，而<1.80 kg/L密度级的斜率比后者稍小；②原料煤的两条回归直线十分贴近，而选煤产品要差一些，这是因为在精煤、中煤中>1.80 kg/L密度级的产率极少，矸石中<1.80 kg/L密度级的产率也极少。

3.2 50～0.5 mm综合粒级中1.60～2.10 kg/L的密度与灰分关系

鉴于50～0.5 mm综合粒级原料煤和选煤产品的<1.80 kg/L及>1.80 kg/L两条回归方程线十分贴近，并有交叉的现象，将它们合并为1.60～2.10 kg/L密度级，推导出相应的回归方程(表5)，并将它们绘于图6。

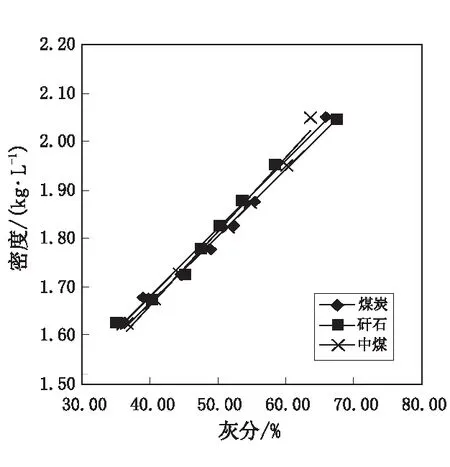
图6 50～0.5 mm综合粒级原料煤和选煤产品的1.60～2.10 kg/L密度的回归线方程Fig.6 The density-ash regression lines of the 1.60-2.10 density fractions in 50-0.5 mm composite size fractions of raw coal feed

从图6中可看出，原料煤、精煤和矸石三条斜直线有良好的重合趋势，中煤却偏离一点。虽然存在微小差异，但从实用性角度出发，可以用50～0.5 mm综合粒级原料煤回归方程代替精煤、矸石的回归方程。而用于预测中煤密度，误差还需进一步探讨。

4 50～0.5 mm综合粒级原料煤的密度与灰分回归方程适用性核算

若能证实50～0.5 mm综合粒级原料煤的密度与灰分回归方程δ=1.121+0.013 7A能适应于各粒级的中煤产品，那么精煤、矸石的应用就不成问题。

为了核算按原料煤回归方程计算的结果与表1所列中煤综合粒级的各粒级平均密度级之间存在多少差异，将成对数据用数理统计t值检测法来核算。表6列出了50～0.5 mm综合粒级中煤各平均密度与原料煤回归方程计算密度差值的t值检验结果。

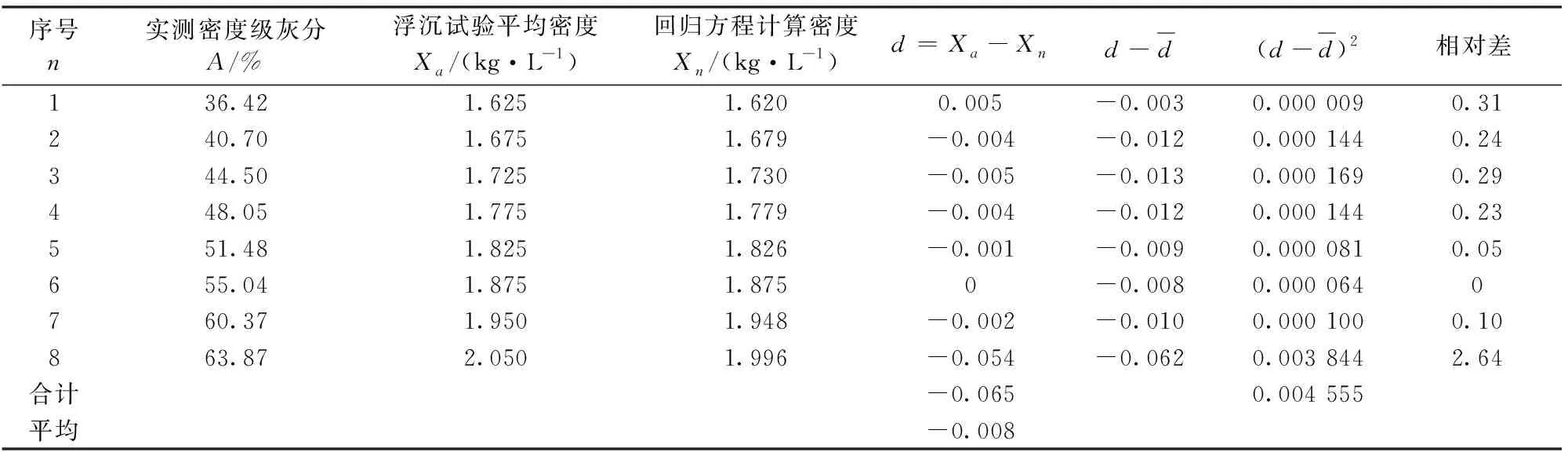
表6 50～0.5mm综合粒级中煤各平均密度与原料煤回归方程计算密度的t值检验表

查t分布表，当自由度φ=8-1=7时，t0.05=1.895，而t

按以上步骤，对各粒级中煤进行了t值检验，检验结果汇总于表7。从表7的数据可知，两者对比无显著性差异，最大相对差为3.13%。因此，50～0.5 mm综合粒级原料煤的密度与灰分回归方程是具有适用性的。

表7 各粒级中煤t值检验汇总表Table 7 A summary of the results of the t-test made on middlings of various size fractions

5 结语

借用重介质旋流器单机检查结果，采集原料煤与选煤产品相关的150余个原始数据，推导了多类可靠性良好的煤炭密度与灰分相关的回归方程48个，对线性回归方程的截距a值、斜率b值进行相互比较，发现它们之间差值小，彼此接近；经数理统计t检验法得出结论，可用50～0.5 mm综合粒级原料煤的密度与灰分回归方程来预先测定各粒级煤炭产品的密度。

在选煤厂投产之前，各粒级选煤产品的具体密度是多少，是无法知晓的，但可借助选煤工程设计必需的煤质资料——原料煤密度组成，建立密度与灰分正相关回归方程，从而可解决这个难题。但本文研究所得出的结论是基于淮南矿业集团谢桥煤矿的原煤性质,是否适用于所有矿井的原煤,有待于更多的研究予以证实。

参考文献：

[1] 周 剑.新疆哈密三塘湖汉水泉矿区煤质特征相关性及应用研究[D].西安：西安科技大学,2015:33-61.

[2] 刘 焱.煤炭灰分、挥发分与真相对密度的相关关系[J].煤质技术,2011(4):14-15.

[3] 武丽丽,吴朝荡,丁光耀,等.煤泥密度与灰分的

正相关性验证[J].选煤技术,2016(1):10-13.

[4] 苏壮飞,王 敏,王兴兴,等.煤泥真相对密度与其灰分正相关关系的再次验证[J].煤质技术,2017(2):61-63.

[5] 路迈西.选煤厂技术管理[M].徐州：中国矿业大学出版社,2005.

[6] 中国国家标准化管理委员会.选煤术语：GB/T 7186—2008[S].北京：中国标准出版社,1987．

[7] 王兴兴，赵宏伟，苏壮飞，等.原煤中矸石密度与灰分正相关关系研究[J].选煤技术,2017(12):23-25．

[8] 陈德奋,程 灏,陈峰峰，等.原煤浮沉基元灰分与密度的线性回归及不确定度评定[J].煤质技术,2015(1):32-33.

[9] 中国国家标准化管理委员会.煤用重选设备工艺性能评定方法：GB/T 15715—2014[S].北京：中国标准出版社,2014.

[10] 中国国家标准化管理委员会.煤炭浮沉试验方法：GB/T 478—2008[S].北京：中国标准出版社,2008.

[11] 樊民强.选煤数学模型与数据处理[M].北京：煤炭工业出版社,2005.

[12] 中国国家标准化管理委员会.煤的真相对密度测定方法：GB/T 217—2008[S].北京：中国标准出版社,2008.

[13] 中国国家标准化管理委员会.煤的工业分析方法：GB/T 212—2008[S].北京：中国标准出版社,2008.

[14] 刘炯天,樊民强.实验研究方法[M].徐州:中国矿业大学出版社,2011:76-79.

[15] 刘 顺.选煤厂设计[M].北京：煤炭工业出版社,1987.