以磁悬浮和螺旋运动结合的太空舱运动形式★

周 莉， 陈佳豪， 田忠建， 蒋婷婷

（重庆大学机械工程学院， 重庆 400044）

引言

从载人航天开始，人类就在如何飞上月球的工具这一问题上进行了钻研创新，产生了空间站，而发射载人飞船极其昂贵的费用和对航天员苛刻的身体条件限制了其发展。但如果能使太空舱在太空中特制的绳索轨道上运行，那高额的运行费用、要求严苛而巨大的能源问题，是否能迎刃而解？

据查，地球半径为6 371 km，月球半径为1 738 km，地月球心距离为384 400 km，在地球与月球之间存在一个地月引力平衡点，即为拉格朗日点，此点距离月球表面为36 702 km。近月的太空站可以建在此拉格朗日点上。模型如下图1所示：

图1 模型图

月球基地与月球太空舱之间可用强度大、质量轻的碳纳米管来连接，使月球天梯在轨道上面运行。而处于热门技术的磁悬浮则是其运动方式的首选。在日本，地球表面的磁悬浮列车最高时速可以达到581 km，受到空气阻力的制约，但太空中处于真空状态，时速可大幅度提高。难点是在太空中建立36 702 km长的真空轨道需要支撑物，远比地球表面困难的多。基于种种因素，可以考虑将磁悬浮与螺旋运动将结合的运动方式。

1 磁悬浮的基本原理

如图2所示，其中从左向右第一幅图为表示两个永磁铁同性磁极相对时产生排斥力，第二幅图表示两个通有反向电流的超导圆线圈相对时产生排斥力，实际情况需多匝线圈，第三幅图表示上部的载流超导圆线圈与理想导体板下面的镜像圆线圈产生排斥力，实际情况需多匝线圈，第四幅图表示异性磁极相对时产生吸引力，上方的电磁铁固定，吸引力使物体悬浮。

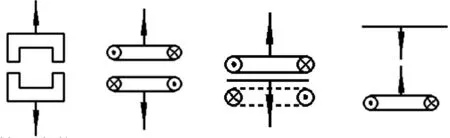
图2 磁悬浮原理

2 太空轨道上太空舱运动方案的选择

由于在太空中无法支撑轨道，则轨道由纳米材料制成的绳索来构成太空轨道，故图2第二幅图所示的磁悬浮原理技术较为实际，并与螺旋传动系统相结合，利用磁极之间的排斥力和吸引力，采用推拉性的推进方式将旋转运动转化为螺旋运动，推拉式原理如下：

参考磁悬浮列车样机所采用的推-拉型磁推进系统的原理[1-2]。在碳纳米轨道上制成外圆为外螺旋的形式，螺旋机构选择传动特性较好的多线螺纹；在太空中由于内外螺旋啮合传动时外螺母要带动外围的太空舱沿着轨道做上升运动，需要承受较大的轴向力，故螺纹牙型选择对中性好、能承受较大轴向力的梯形螺纹。在轨道螺纹的小径表面安装的由超导线圈制成的电磁铁称为轨道电磁铁，在螺母内螺纹的小径安装的由超导线圈制成的电磁铁称为太空舱电磁铁。当螺母沿着装有外螺纹的轨道做螺旋运动时，太空舱电磁铁的极性是恒定的，而轨道电磁铁仅当带动航天器的螺母经过时，该处的轨道电磁铁才按顺序依次接通和断开电流，示意图如下页图3所示，每个图的上排表示轨道电磁铁，下排是太空舱电磁铁（内由135°斜线表示电流正向接通，45°斜线表示电流反向接通，未划线表示未通电）。

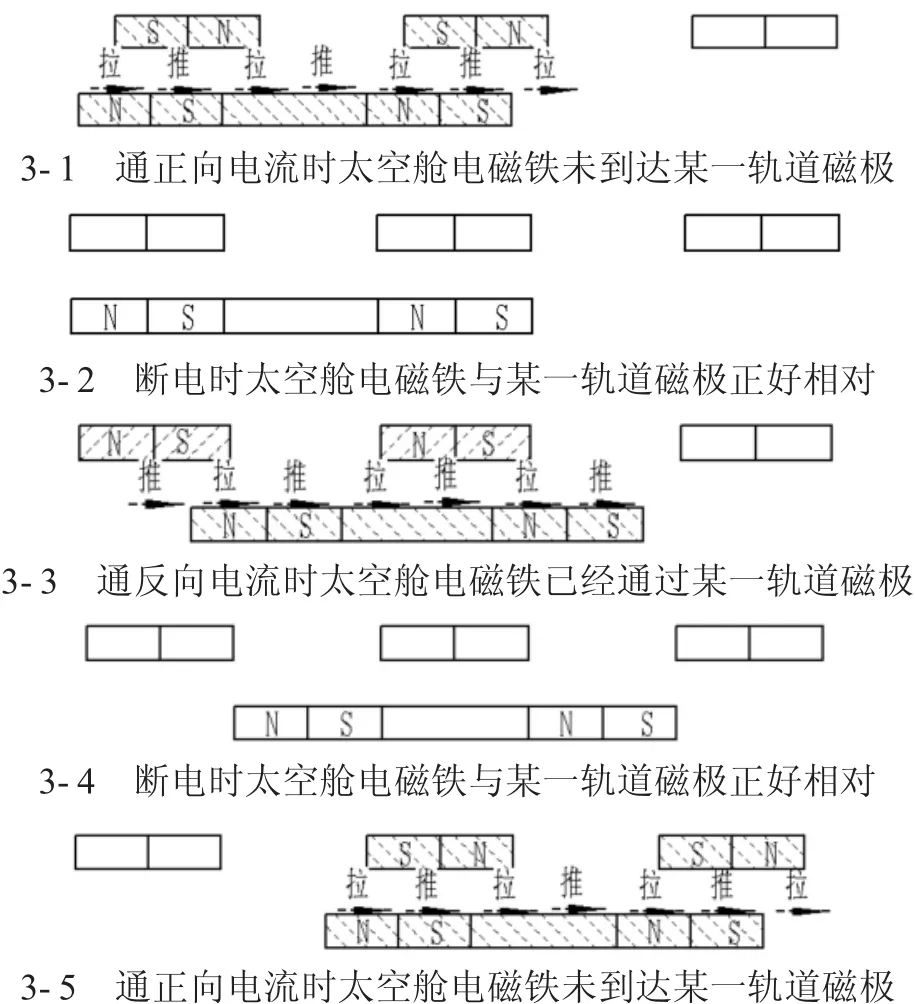
图3 推拉式的电磁铁原理

示意图中根据太空舱电磁铁未到达、刚好到达、已到达某一环节的轨道电磁铁的状态一共分为五个阶段。当太空舱电磁铁到达一组轨道电磁铁之前时（如位置3-1），同时仅有两组轨道电磁铁接通电流,其极性如3-1所示，由于太空舱电磁铁的相对位置,存在四组N-S拉力和三组S-S或N-N推力，所有这些推-拉力的总功效是推动螺母作向前的螺旋运动，从而带动太空舱沿轨道向前运动。当太空舱到达位置3-2时，内外螺纹上安装的磁极正好相对，此时轨道电磁铁的电流被断开，螺母会借助惯性继续作螺旋运动。当太空舱借助惯性到达位置3-3时，轨道电磁铁的电流被接通，但其极性与3-1相反，其结果仍导致推-拉加速，当太空舱到达位置3-4时，轨道电磁铁的电流被断开，太空舱借助惯性到达位置3-5，此时，轨道电磁铁的电流又被接通，其极性与3-1相同。但接通电流的两组轨道电磁铁与3-1有所不同。对比3-1与3-5可知，此时螺母已旋进了图中螺纹长度的2/3。而轨道电磁铁的开关频率会随着轨道电磁铁的长度、间距、以及车速的大小而随之变化。

3 螺旋螺纹的基本参数确定

根据太空中的具体情况，采用滑动螺旋的形式，在太空舱运动过程中，主要承受转矩和轴向力，由于采用了磁悬浮，故旋动是内外螺纹的侧面接触，而螺纹根部未直接接触，故确定其参数时主要依据螺纹牙的磨损及螺杆的受力情况。

3.1 螺纹的耐磨性计算及基本参数确定

耐磨性要求确定滑动螺旋的基本尺寸—螺杆直径和螺母高度[4]。滑动螺旋的磨损与螺纹工作面上的压力、滑动速度、螺纹表面粗糙度及润滑状态等因素有关。由于螺杆采用碳纳米材料制成，碳纳米管的硬度与金刚石相当，所以磨损主要发生在螺母螺纹表面。耐磨性计算主要限制螺纹工作面的压力p，要使其小于材料的许用应力[p]。

参考论文月球天梯系统模型建立和太空舱运动的能耗计算，太空舱共乘坐20到30人，总重为100t。作用在螺杆上的轴向力最大时为Fmax=5.375×105N，被旋合的螺纹工作表面均匀承受，则其工作面上的耐磨条件为：

式（1）中：A为螺纹的承压面积；F为作用与螺杆的轴向力；d2为螺纹中径；P为螺距；h为螺纹的工作高度；Z为旋合圈数，Z=H/P，H为螺母高度；[p]为材料许用应力。

令 Φ=H/d2，带入式（1）中，整理后可得：

对于矩形和梯形螺纹，取h=0.5P；锯齿形螺纹取h=0.75P。式中的Φ，对于整体螺母，由于磨损后间隙不 能 调 整 ，Φ=1.2～1.5； 对 于 剖 分 式 螺 母 ，Φ=2.5～3.5；传动精度较高，要求寿命较长时，可允许取Φ=4。

根据太空轨道的情况，F=5.375×105N[3]，选择梯形螺纹，则取h=0.5P，采用整体式螺纹，则取Φ=1.2。碳纳米材料的强度是钢的80～100倍，钢许用应力在高速下约为1～2 MPa，故可取碳纳米管的许用应力为[p]=80～200 MPa。在太空中强度要求极高，故在此估计计算时用强度最小值，使强度有足够余量。

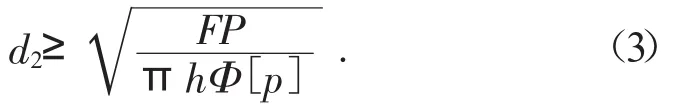
将数值代入公式：可计算出59.72 mm。

查机械设计手册得[5]，选择中径为70 mm，大径为75 mm，螺距为10 mm，公称直径为75 mm的梯形螺纹。

根据公称直径75 mm，螺距10 mm，旋合长度要满足L≥140 mm。太空轨道要求精度很高，可选择右旋螺纹。故螺旋运动基本参数为螺杆螺纹大径75 mm，中径70 mm，小径64 mm；螺母螺纹大径76 mm，小径65 mm。

螺母旋合圈数为：

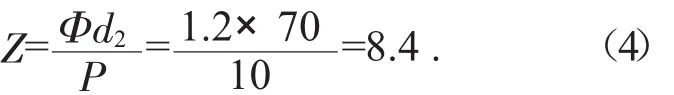
取 Z=9＜10，故合适。

为了进一步提高传动效率，采用双线螺纹传动，则螺纹导程：

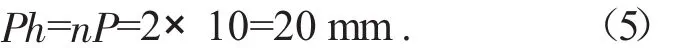
则可得螺母高度：

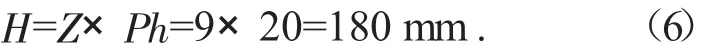
3.2 螺纹升角Ψ的计算

太空舱在太空中运动时，由于太空舱要来回运动，不需要且不能有自锁装置。故可根据螺旋副的传递效率最大来确定螺旋升角。

将螺旋运动展开，可看作是在轴向力FQ的推动作用下一滑块沿螺纹运动。螺母向上旋转时，将螺母看作滑块来分析它的受力情况。将太空舱所受的万有引力以及月球、地球对它的引力看作合力Fa，在运动过程中，磁悬浮对其施加的拉力为F拉，螺纹侧面对它的支持力为FN，摩擦力为Ff，得支撑反力为FR。假设螺旋角为Ψ，摩擦角为μ。受力示意图如图4。

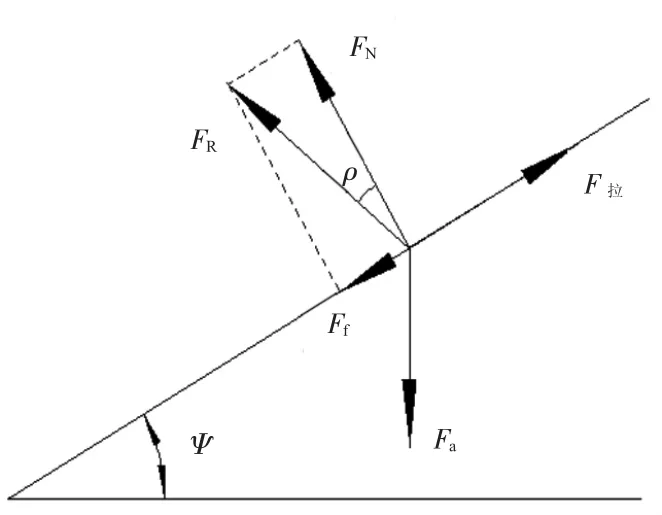
图4 太空舱在轨道上的受力示意图

在太空中，太空舱所受的向心力较大，所以需要磁悬浮力来平衡，即所需磁悬浮力的方向要垂直轨道轴线向外[3]。而在轴向分析中，因为轴向力太大，所以摩擦力不能忽略。故在轴向受力分析中，受力图如图5。由图5可得：

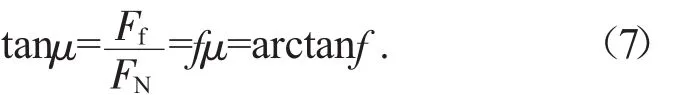
在做等速运动时，三力平衡，且Fa已知，可得：Facos（90-Ψ）+cos（90-μ)=F拉，

FRcosμ=FacosΨ .

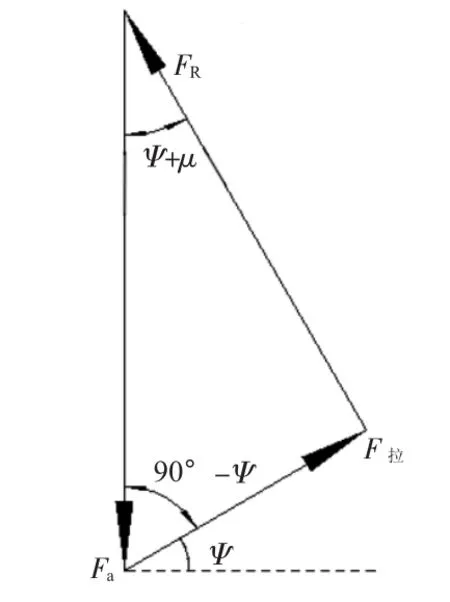
图5 合成受力示意图

由以上两式得：

则可得拉力为：

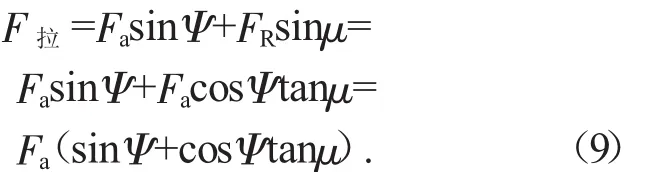
则所需转矩为：

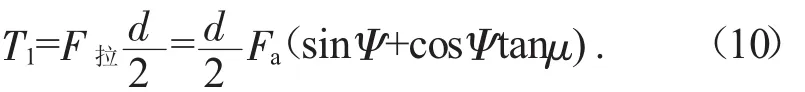
当螺旋运动副运动一周后，输入功为

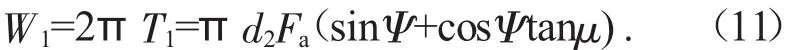
有效功为：

则螺旋副的效率为：

由公式可以确定螺旋升角Ψ：

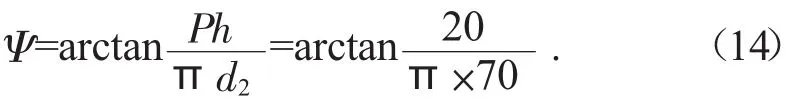
计算得：Ψ=5.2°。

在此螺旋升角下，螺旋传动的效率为（摩擦系数为 0.1）：

计算得

4 螺旋传动与磁悬浮相结合的机械结构

由于太空中需要强度大、质量轻要求较高的材料来建造轨道，故选择强度是钢的100多倍而质量只有钢的1/6碳纳米材料来建造轨道。运动形式选择将摩擦力降低到最小的磁悬浮和螺旋传动想结合的运动方式。碳纳米材料具有很好的导电性能，故可直接将轨道与轨道电磁铁做成一个整体，轨道直径为70 mm，螺距为10 mm，旋合圈数为9圈。螺纹为双线传动。与螺杆旋合的螺母基本参数与之对应。在螺母外围要有滚珠槽，装有滚珠后与太空舱相连接，这样螺母在螺杆上在磁悬浮的作用下作螺旋运动时，会带动太空舱沿着轨道做直线运动，从而使太空舱在轨道上运动。在太空舱运动过程中，由于采用推拉式的磁悬浮推进原理，故轨道电磁铁与太空舱电磁铁（在螺母上面）在旋合时，太空舱电磁铁一直处于得电情况，且其得电的方向不变，即太空舱电磁铁的磁极方向始终保持不变。而轨道电磁铁的得电情况会与之不同，即得电的方向和通断电情况都会发生变化。在太空舱匀速运行阶段，直线运行速度约为200 m/s，螺母和螺杆的旋合长度为可取轨道电磁铁长0.6 m，间距0.4 m，那轨道电磁铁的频率为200 Hz。当太空舱的运行速度提高时，频率也可随之改变。这可由自动控制系统控制。

5 结论

太空舱在绳索轨道上面的运动形式可采用将摩擦力降低到最小的磁悬浮运动和螺旋运动相结合的运动形式。这样建成的月球天梯可以运输载荷，还可以作为载人飞船，开发太空旅游，而成本费用要远比发射载人航天飞船低且能二次利用，并且提供了一种新型的太空舱运动形式，也为未来月球天梯的实现多了一份可能性。

参考文献

[1] 田晓岑，张萍.磁悬浮列车原理简介[J].大学物理，2000（8）：42-43；46.

[2] 王晓光，何畅.磁悬浮飞车原理样机设计及其能耗[J].武汉大学学报（工学版），2013，46（6）：811-814.

[3] 李蒙，陈伟跃，杨胜，等.月球天梯力学特性研究[J].中国空间科学技术，2016，36（3）：63-69.

[4] 李良军.机械设计[M].北京：高等教育出版社，2010.

[5] 于惠力，冯新敏.现代机械零部件设计手册[M].北京：机械工业出版社，1994.