Effects of confinement on rock mass modulus:A synthetic rock mass modelling(SRM)study

I.Vazaios,K.Farahmand,N.Vlachopoulos,M.S.Diederichs

Department of Geological Sciences and Geological Engineering,Queen’s University,Kingston,Ontario,K7L 3N6,Canada

1.Introduction

Design of modern structures built within or on hard rock masses has become more challenging,as the rock-related construction,such as open pit and underground mining,is increasingly getting larger and excavating deeper.As such,the stresses as well as the ensuing stress paths become higher and more complex in nature.Given the fact that such deep excavations are under complex in situ conditions,the development and application of advanced numerical models are essential in order to adequately predict the shortand long-term responses of the rock mass to perturbations caused by engineered alterations.Development of such advanced models requires the introduction to constitutive models with the capability of representing the reality of rock behaviour under different loading paths and deformation states.In terms of continuum-based models(e.g. finite element method models),the deformability and strength of the jointed rock control the material behaviour.In these types of numerical codes,the values of rock mass deformability and strength under different loading conditions(i.e.various confinements and loading/unloading cycles)are de fi ned via constitutive models.It is well-documented(Hutchinson and Diederichs,1996;Martin,1997;Min and Jing,2004;Arzúa et al.,2014)that the values of these two parameters for a given jointed rock are highly dependent on the magnitude of the confining stress acting on the rock.Therefore,the confinement-dependency of such parameters needs to be accounted for in the implementation of the constitutive model.The main objective of this paper is to propose a formula that infers the rock mass modulus according to the magnitude of confining stress that the rock is being exposed to by taking into account other relevant and important factors that affect its deformability.

In order to estimate the deformability of a jointed rock,a socalled synthetic rock mass modelling(SRM)approach is used in which the intact part of the rock and discontinuities are represented respectively by a collection of Voronoi grains,and discrete fracture network(DFN)joints.In order to create such constructs,firstly the appropriateness of an SRM model to estimate the unconfined rock mass strength and deformability needs to be examined.The determination of the mechanical properties of the representative sample is undertaken at a representative volume considering the scale-dependency of the rock mass properties.In order to achieve this,a representative rock mass volume based on the concept of the “representative elementary volume(REV)”is established(Bear,1972;Hudson and Harrison,1997).The determination of the REV size for the studied rock mass is achieved by analysing the geometrical characteristics of the discontinuities(e.g.rock quality designation(RQD),joint spacing,and block volume measurements).Next,the quantified degree of blockiness is served to calculate a range of values for the geological strength index(GSI)(Hoek et al.,1998).By knowing the intact rock strength properties and the rock mass GSI value,the unconfined compressive strength(UCS)and deformability modulus(Erm)of the rock mass are estimated respectively by the empirical Hoek-Brown criterion(Hoek etal.,2002)and the Hoek-Diederichs formula(Hoekand Diederichs,2006)and compared to those obtained from the SRM results at the REV size.Secondly,a series of biaxial compression tests is simulated under various confining stresses in order to investigate the sensitivity of the rock mass modulus to confinement.According to the calculated rock mass modulus,a semiempirical solution is proposed that accounts for the influence of confinement,fracture intensity,and indirectly joint surface condition.This semi-empirical solution can serve as a constitutive model for estimating rock mass deformability based on stress confinement exerted on the elements of a continuum model in order to take into account the effect of the imposed stress state during the excavation stage of an underground project.

To generate and calibrate the SRM models,a systematic procedure(as presented in Fig.1)is followed.Following the explained calibration steps is critical to assure that the model is able to reproduce a reasonable rock mass behaviour.To construct the DFN models,the initial rock mass geometrical information was acquired from a LiDAR three-dimensional(3D)surface model of the Brockville Tunnel located in Ontario,Canada.This information was then used as input in order to feed a DFN generation algorithm and create stochastic joints representing the geometries of pre-existing discontinuities mapped at the tunnel site.

In the next step of the process,the geometries of the stochastic joints are imported into the UDEC code(Itasca,2014)in order to build the SRM specimens.The intact parts of the model are simulated through a dense pack of polygonal-shaped grains forming a grain-based model(GBM).In this method,the grains are bounded and interact with one another at their contacts.Hence,material fracturing can be simulated by breakage of the contacts cohering two adjacent grains.The detachment of grains along their interfaces occurs when the stress level at contacts exceeds the predefined threshold values either in extension or in shear.The mechanical characteristics of a well-established granitic rock(Lac du Bonnet(LdB)granite)reported in Martin(1997)are used to generate and calibrate the intact parts of the SRM samples.In the following,the procedure for generation and calibration of the DFN joints and intact parts of the SRM samples is thoroughly explained.

2.Creation of the discrete fracture network(DFN)

Fig.2.(a)The use of a static terrestrial laser scanner in an unsupported section of the Brockville Tunnel,Ontario,Canada;(b)Generated point cloud from the laser scanning of a 10 m section of the Brockville Tunnel under study;and(c)Creation of a polygonal model of that specific section after meshing the point cloud.

In several engineering applications,the evaluation and assessment of a rock mass can be challenging tasks due to its limited exposure and/or restricted and difficult access to it.However,a solid understanding of the structural features of a rock mass,with a view of understanding its overall behaviour,is necessary in the geotechnical and geological engineering design and construction processes.In order to overcome such limitations,various techniques have been developed and provide a better insight of the expected rock mass behaviour by using multiple scenarios and explore its variability.One of these techniques is the stochastic modelling of fracture networks,which has been the topic of study by various researchers(Baecher,1983;Dershowitz and Einstein,1988;Dowd et al.,2007;Xu and Dowd,2010,2014;Davy et al.,2013).In this technique,joint features,such as orientation,size,density and aperture(ISRM,1978),and their locationsare commonly treated as random variables following a probability distribution.These distributions are usually derived from the collected discontinuity data.Discontinuities found in nature have variable shapes and sizes depending on the geometry of preexisting local and/or regional structures(joints,faults,etc.)and the imposed stress regime.This leads to the creation of rather complex conditions.This inherent complexity is reduced(and idealised)by adopting simpler geometries.Following this approach,it is common practice to treat DFNs in two dimensions as straight lines,while in three dimensions,the joints are considered to be circular or elliptical disks.DFN modelling relies on collecting joint data which can be further processed in order to derive the necessary input parameters for the generation process.These data can be acquired directly by employing scanlines,window surveys,core logging from boreholes,or indirectly by employing remote sensing techniques such as LiDAR scanning and photogrammetry.Once a “data pool”has been created and the input parameters have been determined,multiple DFN models can be created in order to enhance the rock mass assessment and evaluation process.

Fig.3.(a)Virtual mapping of discontinuity surfaces within the 10 m section of the Brockville Tunnel;and(b)The three dominant discontinuity sets that can be identi fi ed within the examined section.Set 1(red),Set 2(blue)and Set 3(green)intersect the tunnel which runs from north to south(light blue)(Recreated after Vazaios et al.,2017).

2.1.Determination of joint parameters based on LiDAR data

The use of remote sensing techniques has become more common in geotechnical and geological engineering practice with a large number of applications,including the identification and measurement of the structural features of rock masses.Discontinuity mapping can be performed on data obtained from laser scanning or photogrammetry and these methods have various advantages when compared to traditional in situ mapping techniques(Feng and Roshoff,2004;Bonnaffe et al.,2007;Haneberg,2008;Sturzenegger and Stead,2009a,b;Fekete et al.,2010;Lato et al.,2010;Lato and Voge,2012;Cacciari and Futai,2016),including increased accuracy of individual measurements,a secure and safe environment for the geologist orengineer performing the mapping,easy access to all the areas where the rock mass is exposed,and reduced measurement biases(Voge et al.,2013).

More specifically,by using a transmitted and reflected laser beam,LiDAR scanning results in the recording of millions of high accuracy points in a 3D space,hence forming a ‘point cloud’(Fig.2b).Further processing of a point cloud leads to the creation of a polygonal model by meshing the individual points of it(Fig.2c).This can improve the interpretation of the obtained data and is rendered necessarily when continuous surface information is required(Sturzenegger and Stead,2009a,b;Fekete et al.,2010;Lato and Voge,2012;Voge et al.,2013).Discontinuity features including orientation and spacing can be measured directly within the polygonal model by identifying discontinuity surfaces and traces.Other features such as the size can be estimated indirectly based on the observed trace lengths.Research has also been done on estimating the roughness by using remote sensing techniques(Fardin etal.,2004;Sturzeneggerand Stead,2009a,b;Millsand Fotopoulos,2013).However,the “virtual mapping”of joints within LiDAR data is subjected to biases due to the scanning(Lato et al.,2010),and inherent biases of the data collection processes applied(Watkins et al.,2015),including scanlines and rectangular mapping windows,which also have to be considered.

In regard to the geometrical modelling of rock masses,when DFN models are used,orientation,number of joint sets,joint density,and joint size are the key input parameters as they inherently control the geometrical characteristics of the natural fracture networks.According to Step 1 of the DFN modelling of the flowchart in Fig.1,in order to obtain discontinuity data for the purposes of this study,the polygonal model of a section of the Brockville Tunnel was used(Vazaios et al.,2017).A 10 m length section of the approximately 5 m tall horseshoe tunnel was captured using a terrestrial laser scanner.The data were then processed using Polyworks software(Innovmetric,2016).The virtual mapping performed included the identification of joint surfaces and traces which were explicitly mapped within the polygonalmodel.Joint surfaces can be identified by fitting planes on selected areas(Fig.3a),and the dip and dip direction of these planes can be measured by using the direction cosines of the normal vector of the respective plane.By repeating the same process for multiple joint surfaces,a stereonet analysis can be conducted in order to determine different joint sets and their respective mean planes.Therefore,by following Step 2 of the DFN modelling process in Fig.1,the stereonet analysis was conducted for the 10 m section of the Brockville Tunnel using DIPS(Rocscience,2006).The results are illustrated in Fig.3b,with the obtained orientation measurements shown in Table 1.Three joint sets are dominant with their mean orientations being:Set 1:285°/88°,Set 2:77°/12°,and Set 3:207°/77°,respectively.

By applying a similar approach(Step 2 of DFN modelling process in Fig.1),the joint traces can also be mapped within the polygonalmodel by fitting polylines,which is demonstrated in Fig.4a.Since discontinuities are 3D features,estimating their size and shape can be an onerous task,as typically,a limited surface of the rock mass is exposed.Therefore,only indirect estimates can be made based on the mapped traces.In this particular case,the measured length of the joint traces is used to determine the size of the generated joints based on a trace length distribution,as suggested by Srivastava(2006),which is demonstrated in Fig.4b.Each of the three curves corresponds to Set 1(red),Set2(blue)and Set3(yellow),respectively.This methodology is based on a cumulative length distribution for specific trace length thresholds,and for each of these,the cumulative number of joints is specified.It should be noted that for the fracture trace mapping of Set 1,a complementary polygonal model of the scanned roof of the tunnel was used.The joint trace data obtained from the roof provide the necessary information for the derivation of the cumulative distribution for Set 1.The output data obtained from processing the trace lengths are summarised in Table 2.For the purposes of this paper,the tangent of the aforementioned curves(Fig.4b)is determined and used as input for the DFN generation algorithm.The tangent of each curve is defined by pointsAandBwithXbeing the trace length threshold andYbeing the cumulative number of joints per area,as shown in Table 2(Step2 of DFN modelling in Fig.1).These points are used by the DFN generation algorithm of the MoFrac software(Mirarco,2015).Intersections and terminations of traces can also be identified and recorded resulting in a truncation matrix(as illustrated in Table 3).The truncation matrix depicts what percentage of the joints of one specific joint set terminates or not on another joint set.This matrix can be used to prescribe the number of joints terminating against another when a DFN model is generated similarly to UDEC(Itasca,2014).

Table 1Discontinuity orientation of the dominant sets of the examined tunnel section(Modified after Vazaios et al.,2017).

Fig.4.(a)Virtual mapping of joint traces within the 10 m section of the Brockville Tunnel;and(b)The cumulative trace length distributions of the three dominant discontinuity sets.Set 1(red),Set 2(blue)and Set 3(yellow)are highlighted(Recreated after Vazaios et al.,2017).

Table 2Fracture trace measurements within the LiDAR data for the 10 m section of the Brockville Tunnel and derived DFN modelling parameters(Modified after Vazaios et al.,2017).

Table 3Fracture truncation matrix for the 10 m section of the Brockville Tunnel.The columns indicate the percentage of a discontinuity terminated on another discontinuity set(Modi fi ed after Vazaios et al.,2017).

2.2.Generation of stochastic joints using DFN modelling

After obtaining the required input parameters for the geometrical modelling of the given rock mass,based on data collected using LiDAR scanning,multiple DFN models were created.MoFrac has the capability of using both the normal(Gaussian)and the Fisher distribution in order to simulate the variability of the joint orientation of the generated discontinuities.For the purposes of this study,the Fisher distribution was used along with the dip and dip direction of the mean planes for Sets 1,2 and 3,and the Fisher constantKfor each discontinuity set is presented in Table 1.

The mapped fractured traces are used to “seed”a fracture propagation algorithm and the fracture size is determined based on the tangent of the derived cumulative length distribution curves(Fig.4b).Therefore,the areal fracture intensityP21,which is defined by Dershowitz and Herda(1992)as the fracture total length per area,is used indirectly in order to determine joint locations and joint size.Furthermore,the mapped joint traces are used to create deterministic joints(Fig.5b)at specific locations while the cumulative distribution curves are used to generate stochastic ones(Fig.6)(Step 3 of DFN modelling process in Fig.1).More specifically,the modelling procedure initializes with creating deterministic joints and small(“point”)joints,both of which have tips that can grow.Once the volume of interest has been populated by the deterministic and stochastic joints,a statistical model of spatial continuity(variogram)of joint orientation is created.An iterative process initiates in order to determine the joint size in three dimensions.By employing a Gaussian simulation scheme,the direction of joint growth is estimated based on the surrounding joints and conditioning information.This process is repeated by propagating the crack tips until the target joint length distribution,and hence the target areal fracture intensity,has been achieved.

2.3.Calibration of the DFN model

Once the joint input parameters were established,the rest of the required parameters for the stochastic processes taking place,during the generation,need to be determined.The 3D surfaces representing the joints within the DFN model consist of a triangulate mesh.Parameters including mesh resolution and element size need to be determined,in order to satisfy the applied mathematical model and generate the DFN model.These input parameters,which cannot be obtained directly from the LiDAR data,are estimated via an iterative process until they have been properly calibrated based on the mapped joint traces,according to Step 3 of the DFN modelling process in Fig.1.This calibration process is employed in order to achieve a match between the in situ mapped joints and the deterministic simulated joints at the exact locations,as described in Vazaios et al.(2017).

Fig.5.Calibration process of the DFN model for Brockville Tunnel.(a)“Virtual mapping”of the joint traces on the right wall of the tunnel for a 10 m section;(b)The extracted joint traces;(c)Deterministic joints generated using MoFrac for Sets 2 and 3;and(d)Joint traces derived from the DFN model(Set 2:blue,and Set 3:yellow)and their corresponding mapped joint traces(black).

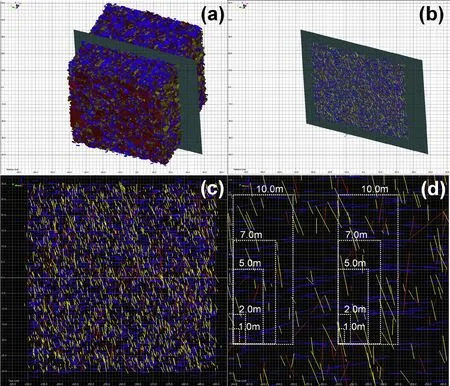
Fig.6.(a)A 60 m×60 m×60 m DFN model of the Brockville Tunnel(Set 1:red,Set 2:blue,Set 3:yellow),(b)two-dimensional(2D)cross-section of the 3D DFN model,and(c)the joint traces corresponding to the examined plane.(d)Sampling of the 2D cross-section in order to create rectangular samples of different sizes with a view to be imported into UDEC.

Fig.7.Cumulative length distribution curves based on the measured joint traces mapped within the 10 m section of the Brockville Tunnel for(a)Set 1(red),(b)Set 2(blue)and(c)Set 3(yellow)along with the respective best fit curves for the observed joint traces.In a similar fashion,for 10 different 2D mapping windows(sections)within the 3D DFN model at random locations(see Fig.6d),the joint traces are extracted and processed in order to obtain their cumulative length distributions per joint set respectively.The 10 different distributions per joint set obtained are then averaged and the average joint trace curve from the DFN model(black)is compared to the one from the mapped joint traces(Modified after Vazaios et al.,2017).

Fig.8.Schematic showing a 2D rectangular mapping window and the extracted“virtual”drill core sample from the DFN model to measure the RQD of the rock mass.The RQD is estimated by measuring the length of “intact core”between the intersection points of the joints with the borehole axis denoted as x1,x2,…,xn.

The calibration process includes the following steps:

(1)Generation of a deterministic DFN model(Fig.5c)using the LiDAR derived input data(Fig.5a and b).

(2)Extraction of joint traces from the simulated data(Fig.5d).

(3)Comparison between simulated joint traces and observed in situ joint traces(Fig.5d).

(4)Steps 1-3 are repeated until a satisfactory match has been achieved.

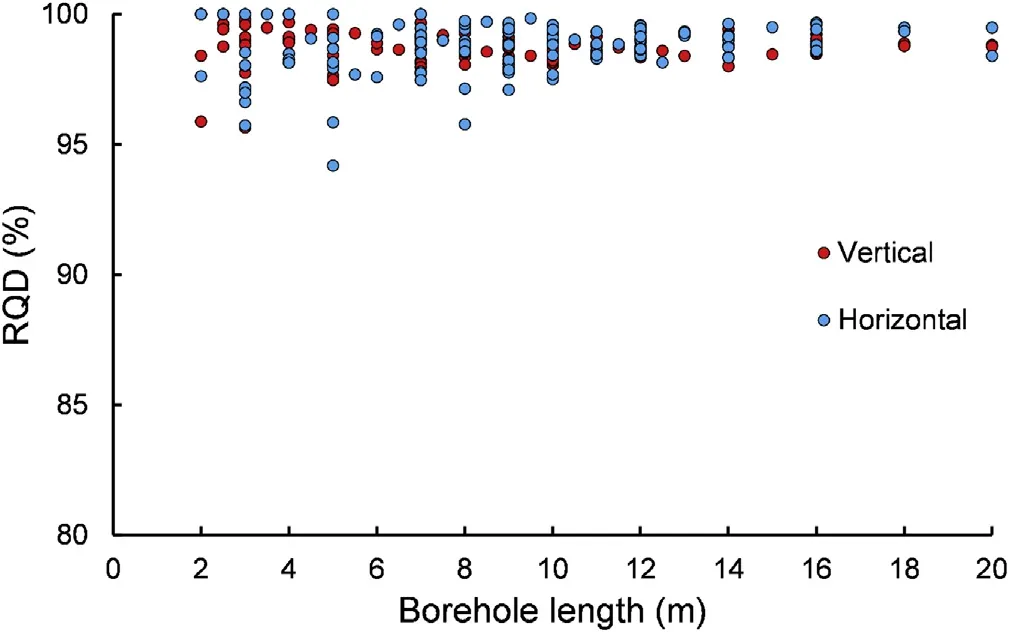
Fig.9.Evaluated RQD from the “virtual”rock cores extracted from boreholes of various lengths.

Fig.10.Histogram showing the distribution of joint spacing measurements from the DFN model.

Fig.11.Influence of the size of the sampling area on the areal fracture intensity P21.

2.4.Validation of the stochastic DFN model

After the calibration of the deterministic DFN model based on the mapped joint traces,models of larger volumes can be generated.The volume of interest is the parameter that controls the size of the stochastic model and once specified,stochastic processes are employed in order to fill the volume of interest based on the selected input parameters.For the purposes of this study,a volume of 60 m×60 m×60 m was employed,in order to eliminate possible boundary effects,and 30 different realisations were created(Fig.6).

The generated DFN models need to be validated in order to ensure that they are representative of the modelled rock mass.In order to achieve this,rectangular mapping windows of 10 m×5 m were employed and the generated joint traces were extracted(DFN modelling Step 4 in Fig.1).The selected dimensions of the mapping windows are similar to the dimensions of the examined section(Fig.4a)in order to have the same reference mapping area when comparing the simulated joints with the observed in situ ones.The joint traces were mapped in Polyworks,and based on the acquired results,the trace length curves were derived for every mapping window(Fig.7).Since the DFN modelling is a stochastic process,there is variability resulting in a cloud of points surrounding the length distribution curves derived from the LiDAR data.These points are averaged and a “mean”distribution is created and compared to the one corresponding to the “in situ”observations for every discontinuity set respectively.From Fig.6,it can be inferred that the cumulative length distribution curves for the simulated fractures are similar to the ones derived from the “in situ”observations,and therefore the DFN model can be considered representative of the given rock mass.

3.Deriving input parameters for rock mass classification systems based on the geometrical analysis of the DFNs

Fig.12.Example of rectangular samples of four different sizes(1 m,4 m,7 m and 10 m)created in 3DEC after importing the DFN geometry.

The collection and analysis of qualitative and quantitative data are indispensable parts of the rock mass characterisation process in order to determine a means for estimating the geometrical and mechanical properties of a rock mass.Rock mass classification schemes have been created to classify rock masses and provide quick and reasonable estimates of their mechanical properties,quantitative data for support estimation,and enable the communication between the site investigation,the design and construction processes.Among the most popular proposed classification systems,including the RQD(Deere,1968),rock mass rating(RMR)(Bieniawski,1976),Q(Barton et al.,1974),GSI(Hoek et al.,1998)and RMi(Palmstrom,1996),the GSI system seems to be more flexible because it can provide a complete suite of input parameters for numerical analysis which can be a great asset during the design process(Cai et al.,2004).

Fig.13.Block volume distributions for(a)slightly,(b)moderately,and(c)morejointed rock masses based on the DFN model extracted from three random locations.The 1 m,2 m and 3 m sample size volume curves have been highlighted in order to show the effect of the sample size(scale-dependency)and how it moves the volume distribution to the right as the sample size increases.

Fig.14.(a)Average block volume based on the 50%passing(D50),(b)uniformity coefficient(D60/D10),and(c)gradation coefficient(D230/(D60D10))for various sample sizes extracted from three random locations.

However,two main issues may be encountered when employing the GSI system for the rock mass assessment:(1)determination of a reliable value for the index itself due tothe qualitative nature of its determination,and(2)the amount of exposure and access to the rock mass for a reliable estimate(depending on the in situ conditions and project specifications).The original GSI was meant to be used by qualified and experienced geologists or geological engineers.In many situations,however,the data are not collected by individuals with adequate and specific geological knowledge of a particular site resulting in estimation of GSI values that are not indicative of the rock mass strength.This led researchers to focusing on the quantification of the original qualitative descriptions by using well-established indices,such as the RQD(Hoek et al.,2013),or joint spacing/block volume(Cai et al.,2004).The issue regarding the availability of sufficient rock exposure solely depends on the site-specific conditions and the project requirements.In tunnelling,specifically,the initial estimates are based on primarily surficial geology(in addition to borehole data)that may not be indicative of the conditions at depth.

In such cases,DFN modelling can be proven to be a valuable tool in order to evaluate the rock mass condition.This can be achieved by creating a number of DFN models considering various scenarios(within the context of a parametric study)for joint network geometries,resulting in a better understanding of the possible range of the GSI.Moreover,DFN models can also be combined with sophisticated numerical methods in order to create SRM models.These models can be used to make estimates for the strength and deformability of the rock mass under investigation.In this paper,the stochastic joint geometries were firstly used to derive the RQD,joint spacing,and block volume for the studied rock mass(within the methodology as shown in Fig.1).These geometrical indices,which define the degree of blockiness,were used to quantify the GSI.Furthermore,the DFNs were introduced to the UDEC-Voronoi model,as described in Section 4,in order to compare the mechanical properties derived from the numerical models with the properties obtained from the empirical methods.

Additionally,it should be noted that the geometrical and mechanical properties of the rock mass are a function of the scale at which the rock mass is being examined(Bear,1972;Hudson and Harrison,1997).In order to address the scale-dependency of the rock mass properties,and to reduce associated effects,the variabilities of the strength and deformability with respect to the size of the specimen are required to be investigated.Within this context,the geometrical REV is established for the DFN models based on the analysis of the measured RQD,areal fracture intensity(P21),and block volumes.This process leads to the determination of a specimen size which includes a sufficiently large number of structures and that specific size can be considered representative for the overall rock mass conditions.

Fig.15.Model configurations for(a)intact SRM specimen,and(b)jointed SRM specimen.Grains with purple,light red,light brown,and dark red represent K-feldspar,plagioclase feldspar,quartz,and biotite minerals,respectively;and the histogram is showing the percentage of the different mineral phases in the real LdB granite and the SRM model.

3.1.RQD and discontinuity spacing measurements

RQD is typically assessed by examining retrieved cores from boreholes and in a similar fashion,“virtual”boreholes were created vertically and horizontally within the DFN model,as illustrated in Fig.8.In Fig.9,the average RQD values(obtained from 2975“virtual”boreholes)are plotted versus the borehole length in order to investigate the effect of the sampling size via the length of the boreholes.As illustrated,most RQD measurements are within the range of 95%-100%.This infers that RQD is not sensitive to the borehole sampling length.However,it can be seen that the measurements tend to be more scattered for lengths less than 6 m.

Furthermore,the spacing between the discontinuities was evaluated from the “retrieved”core.Fig.10 demonstrates the spacing distribution based on 1352 measurements from the DFN model and a mean joint spacing of approximatelySa=0.6 m was derived.Since more than one joint sets are present,the calculated average spacing,Sa,is used to make an preliminary estimate for the average block volume sizeVbusing the formulaVb=S3a(Palmstrom,2005).Based on this formula,the average block volume is approximately 0.24 m3.Snow(1968)suggested that the REV size for a given rock mass is approximately 10-20 times the mean spacing of joints.Schultz(1995)suggested that the REV size is approximately 5-10 times the joint spacing.Given the mean spacing of 0.6 m for the Brockville rock mass,the REV sizes of 6-12 m and 3-6 m were determined based on Snow(1968)and Schultz(1995),respectively.

Table 4Micro-material properties for different minerals of LdB granite.

3.2.Areal fracture intensity measurements

Next,within the context of the overall methodology,the areal fracture intensityP21was measured and the influence of the size of the sampled area was assessed by using 1212D rectangular mapping windows of various sizes with a height-to-width ratio equal to 2.5(Fig.11).In order to select the appropriate REV size for a specific property,the coefficient of variance(CoV),defined as the ratio of the standard deviation to the mean value,was used.As shown in Fig.11,theCoVofP21for the sample sizes smaller than7m is more than 20%.This indicates that the number of joints included within the specimens smaller than 7 m is not representative for the overall rock mass.On the contrary,for specimen sizes larger than 7 m,theCoVdrops below 20%(Esmaieli et al.,2010),indicating that the population of structural entities within the specimens is sufficient to be representative for the rock mass conditions.Therefore,a geometrical REV of 7m is established and theP21within the range of 2-3m/m2is achieved for the specimen sizes larger than the REV size.

3.3.Block volume measurements

After performing the linear and areal measurements,more detailed block volume measurements were conducted in order to verify the preliminary block volume assessment presented in Section 3.1.The 3DEC code(Itasca,2013)was used to evaluate the volume of the blocks forming between DFN joints.In order to conduct this analysis,the DFN geometries of various sizes(height/width=2.5)are imported into the code,as shown in Fig.12.It should be noted that only discontinuities forming complete blocks are taken into account.Hence,smaller discontinuities are deleted as they fail to form blocks,resulting in slightly larger blocks than the actual rock mass condition.Additionally,it can be observed in Fig.12 that smaller size samples have few blocks forming within their boundaries than the larger samples,which shows the scaledependency of the block volume measurements conducted for different sample sizes.

In Fig.13,the obtained block volume distributions are illustrated for three different random locations within the master-volume DFN model of size 60 m×60 m×60 m.It can be observed that the genetic algorithm used for the generation of the DFN results in areas with a presence of less joints(Fig.13a than other areas(Fig.13b and c),hence favouring the formation of larger blocks at specific locations.More specifically,from Fig.14a,it can be observed that for Locations 1,2 and 3,the block volume corresponding to 50%passing(D50)is approximately 2.3 m3,0.77 m3and 0.25 m3,respectively,hence showing that the variation in the joint conditions simulated influences the size of the blocks created.This is in agreement with the fracture intensity measurements in Fig.11,in which it can be observed that the fracture intensity does not have a constant value.On the contrary,the fracture intensity has a range indicating that there are locations where the rock mass is more fractured than other locations,and therefore blocks can be smaller than those in other locations where sparser joints form larger blocks.

Fig.16.Cohesive crack model.Stress-displacement behaviour of the cohesive contact model in(a)Mode I,(b)Mode II,and(c)mixed-Mode I and II.(d)Bilinear failure criterion with residual strength and tension cut-off to define the strength properties of the contacts in shear and tension(Farahmand,2017).

By examining the volume of the 50%passing(D50)relative to the size of the sampled specimens,it can be inferred that for samples greater than 6 m,the block volume becomes approximately constant with only small fluctuations(Fig.14a).Furthermore,the coefficients of uniformity(D60/D10)and gradation(D230/(D60D10))(Fig.14b and c,respectively)show that the block volume distributions per location have approximately the same characteristics for sample sizes greater than 7 m,while for smaller sample sizes,they do not maintain a specific value and the deviations between each examined size are significant,showing that a representative value for the rock mass cannot be obtained.The established geometrical REV size(presented in Section 3.2)is consistent with the block volume measurements.Therefore,a 7 m sample is considered representative of the whole rock mass.Blocks formed have an average range of volumes from 0.23 m3to 2.3 m3.Moreover,the lowest end of the volume range is in agreement with the estimated block volume value obtained fromVb=S3a(Palmstrom,2005),while it underestimates the average block volume estimated in this section.

Table 5Calibrated micro-mechanical properties for contacts.

4.Appropriateness of the SRM approach to estimate rock mass mechanical properties

In this section,the SRM approach and empirical GSI system are used to estimate the mechanical properties of the rock mass and their associated scale-dependency.The SRM estimations for the strength and deformability are compared herein with those properties obtained from the empirical method in order to investigate whether the SRM results match the empirical method estimations.To do so,the quantified degree of blockiness obtained in Section 3 is used to calculate a range of values for the GSI(Hoek et al.,1998).Having obtained the intact rock strength properties and the rock mass GSI value,the UCS and deformability modulus(Erm)of the rock mass were estimated respectively by using the empirical Hoek-Brown criterion(Hoek et al.,2002)and the Hoek-Diederichs formula(Hoek and Diederichs,2006),and were compared to those obtained from the SRM results.

The SRM samples(Fig.15)consist of four different mineral grains:potassium-feldspar grain,plagioclase-feldspar grain,quartz grain,and biotite grain(GBM modelling Step 1 in Fig.1).The percentage of each mineral grain in the model was selected according to the mineral composition of the LdB granite(Table 4).The average grain size for the LdB granite is approximately 2.5 mm.However,generating the model according to this grain size would be computationally impractical due to the time required to conduct the analyses.Therefore,in order to keep the required run times within a practical range,an average grain size of 3 cm was adopted to generate the models.This grain size is small enough,relative to the overall size of the model,in order to avoid the grain size dependency of fracture patterns.

A cohesive crack model is implemented into UDEC to de fi ne the force-displacement relationship of the contacts in opening,sliding,and mixed opening-sliding modes(GBM modelling Steps 2-5 in Fig.1).This constitutive model controls the contact bonding stress based on the grains’relative displacements in the normal and tangential directions.In both opening and sliding conditions(Fig.16a and b),the stress-displacement curves are composed of two branches with a hardening section representing the response of a contact prior to yielding and a softening section defining the post-peak behaviour of the yielded contact.The response of the model in opening mode(tension)depends on the initial normal stiffnesskn0，c,the tensile strengthTc,and the Mode I fracture energy release rateGIc.In sliding mode(shear),the initial shear stiffnessksh0，c,the shear strengthfsh,and the Mode II fracture energy release rateGIIccontrol the behaviour.The peak shear strength is governed by

Therefore,according to the cohesive model adopted in this study,the contacts between the grains are able to break in tension(Mode I),shear(Mode II),or a mixed mode I-II as a result of the generated local stresses and the relative contact displacements.UDEC built-in contact models,such the Coulomb slip and the continuous yielding model,are used to simulate the damage of contacts under shear.While these models are able to capture and are used for the simulation of joint behaviour,they are not well suited for capturing hard rock fracturing.On the contrary,the nonlinearity of the employed cohesive crack model both in the prepeak and post-peak regions is able to capture both the decay of stiffness in the pre-failure state,due to the damage progression on the contact interface,and the post-peak softening of the material,as a result of damage accumulation and energy dissipation.Such a model is able to capture realistically the complex fracturing mechanisms of hard rocks.

Table 6Comparison between experimental and simulation results for the LdB granite(experimental data are given from Martin,1993).

In this paper,a systematic calibration procedure(GBM model work flow),as outlined in the flowchart presented in Fig.1,was followed.This calibration procedure is an iterative process that involves running a series of Brazilian,UCS,and biaxial simulations to find a set of input parameters that yields the correct macromechanical response of the tested rock.The step-by-step calibration process is discussed in detail in Farahmand and Diederichs(2015).Since the models are composed of four different mineral phases,10 contact types need to be calibrated.The calibrated contact properties for 10 interfaces of the model are given in Table 5.It should be noted that the values of Mode II fracture energy releaseGIIcare assumed two times the value ofGIc.The obtained macro-mechanical properties of the SRM model are compared to mechanical properties of the LdB granite in Table 6.

The material properties of the joints were assigned according to Table 7(Nirex,1997).A Coulomb slip with residual strength is used to control the behaviour of joints in shearing.The residual strength simulates displacement-weakening of the joints by loss of cohesion and friction at the onset of shear yielding.Additionally,the joints are considered open and an initial aperture is assigned to them.During the simulation and under different stress states developing in the specimen,as a result of the applied compressive load,the joint openings are able to close until the assigned value for a residual aperture has been achieved.For more information,the reader is referred to Farahmand(2017).

In order to have an estimate of the strength and deformability based on an empirical approach,the GSI was evaluated from the observed structural features of the Brockville rock mass and the joint surface condition based on well-established data in the literature from the Sellafield site(Nirex,1997).In order to quantify the degree of blockiness of the rock mass,three parameters including RQD,joint spacing,and block volume are considered(Cai et al.,2004;Hoek et al.,2013),based on measurements presented in Section 3.This provides a more objective quantitative index of the structure of the rock mass.It is assumed that the joint condition is fair with the smooth,moderately weathered and altered joint surface which corresponds to the third column of the GSI chart(Fig.17)according to data reported in Nirex(1997).

According to the empirical correlation(Eq.(2))proposed by Hoek et al.(2013),the RQD measured from the DFN model using“virtual”boreholes(Figs.8 and 9)is used as an input to measure a range for GSI.The predicted GSI range is approximately 66-77 as illustrated in Fig.17(left,coloured region).

Table 7Properties assigned to the pre-existing joints of the SRM models.

Fig.17.The range of the GSI estimated for the Brockville rock mass based on the GSI charts proposed by Hoek et al.(2013)(left),and Cai et al.(2004)(right).Coloured regions in the charts indicate the range of the estimated GSI.(Left)The green ellipse indicates the range of GSI estimated from RQD value and joint condition of the synthesized rock mass.(Right)The estimated ranges of GSI based on mean joint spacing and block volume are shown with blue box and red box,respectively.

whereJCOND89is the joint condition rating de fi ned by Bieniawski(1989).

The second approach involves the estimation of the GSI based on the measured spacing and block volume.For an approximate spacing range between 0.5 m and 1 m(Fig.12)and for block volumes between 0.23 m3and 2.3 m3(Fig.13a),the estimated GSI ranges from approximately 50 to 65 and 50 to 67,respectively,as illustrated in Fig.17(right,coloured region).

Based on the obtained GSI values,the UCS of the examined rock mass is estimated and the strength thresholds are illustrated in Fig.18.Fig.18 compares the estimated UCS of rock mass obtained from the SRM simulation for various sample sizes and those determined from the generalised Hoek-Brown criterion.The RQD-based GSI approach leads to UCS values of rock mass closer to those for the SRM specimens at the REV size of 7 m.Using the joint spacing and block volume toestimate the GSI results in the strength values between 13 MPa and 40 MPa,which are lower than the UCS values obtained from the SRM simulation.The analysis of different geometrical features of the rock mass with an emphasis to the RQD in this case can provide a good first estimate of the UCS of rock mass.In general,the SRM strength prediction matches reasonably well with the results obtained from the Hoek-Brown criterion,given that the input GSI value has been determined correctly and represents the reality of the rock mass conditions.

In a similar fashion,the Young’s modulus of the rock mass is also estimated based on the acquired GSI values from the assessment of the geometrical properties of the rock mass.For the estimation of the rock mass modulus,the Hoek-Diederichs formula(Eq.(3))(Hoek and Diederichs,2006)is used.A disturbance factorofD=0 is considered in order to estimate theErm.

As illustrated in Fig.19,the GSI estimate based on the RQD values results in a larger value for the modulus of the given rock mass when compared to the case in which the discontinuity spacing and the block volumes are used to determine the GSI.More specifically,the estimated range is from 50 GPa to 60 GPa.The RQD-based GSI results in a larger stiffness for the rock mass,however,the spacing and volume based GSI values yield a closer approximation to the Young’s modulus resulting from the SRM simulations with its range being between 21 GPa and 50 GPa.

Table 8 summarises the achieved REVs for the rock mass properties.An ultimate REV of 7 m is established according to the results of scale-dependency investigation of the geometrical and mechanical properties.

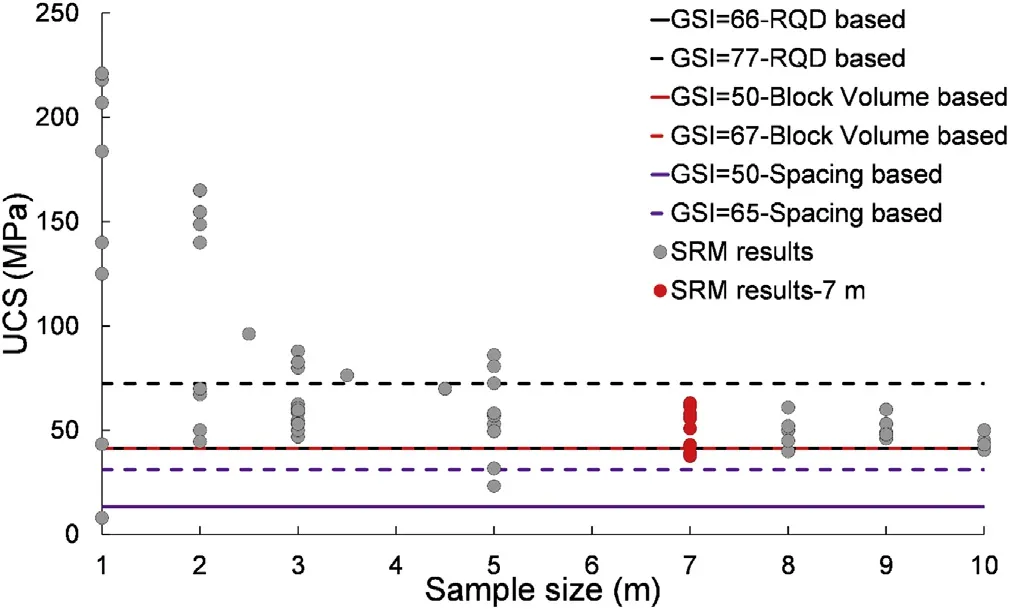
Fig.18.UCS obtained from different GSI values based on the assessment of the geometrical features of the investigated rock mass.The suggested empirical thresholds are compared with the numerical results based on the conducted SRM for 7 m samples based on the determined REV size.

Fig.19.Rock mass modulus obtained from different GSI values based on the assessment of the geometrical features of the investigated rock mass.The suggested stiffness thresholds are compared with the numerical results based on the SRM conducted for 7 m samples based on the determined REV size.

Table 8Summary of the REV determination(Farahmand,2017).

5.Degree of jointing and its effect on the rock mass mechanical properties

In this section,the impact of the severity of jointing on the resultant UCS and deformability of rock mass is investigated,with the degree of jointing in the specimen being represented by the areal fracture intensity(P21).Fig.20 compiles the UCS for granitic rocks.The plotted data for the UCS of the intact LdB granite(P21=0 m/m2)are taken from laboratory testing results(black dots)reported by Martin(1997).The UCS data demonstrating the strength of the Brockville SRM models at the REV size of 7 m(DFN model used illustrated in Fig.21a)withP21=2.5 m/m2are plotted with red dots.The strength data for the case of highly jointed granite withP21equal to approximately 18 m/m2are also shown in Fig.20.Noorian Bidgoli et al.(2013)generated DFN specimens(as shown in Fig.21b)based on the joint geometrical information collected from a site characterisation program at the Sellafield area,Cumbria,UK of the Sellafield site as reported in Nirex(1997).A number of DEM simulations were carried out on the DFN specimens at REV of 10 m×10 m to estimate the UCS of rock mass.It should be noted that the same mechanical properties,as listed in Table 7,are assigned to the joints of both Brockville and Sellafield models.The mechanical properties assigned to the intact blocks of the Brockville model(Ei=69 GPa,UCSi=220 MPa,vi=0.22）and the Sellafield model(Ei= 84 GPa,UCSi= 157 MPa,vi=0.24）are close,sothat the estimated UCS results could be used in order to investigate the effect of jointing on the rock mass strength.An exponential function is fitted to the strength data plotted in Fig.20.Numerical studies reported by Hamdi et al.(2015)suggest a similar exponential relationship between the degree of microcrack damage in the intact LdB granite and the simulated UCS.

A similar analysis is performed to assess the unconfined rock mass modulus of jointed rocks.Similar to the UCS case,an exponential function is fitted to the data presented in Fig.22.The rock mass modulus data for the case of the highly jointed rock mass(P21=18 m/m2)are obtained from the numerical simulations of the DEM-DFN specimens representing the Sella fi eld rock mass,as reported in Min and Jing(2004).

Fig.20.The effect of areal fracture intensity P21on the UCS of fractured rock masses.The effect of large-scale structures within the rock is highlighted by using UCS data of the LdB granite representing the peak strength of the rock,UCS results obtained from the SRM of the fracturing conditions of the Brockville site,and DEM results for a highly fractured rock as reported in Noorian Bidgoli et al.(2013).The effect of microcracks in granitic rocks based on numerical modelling by Hamdi et al.(2015)is provided for comparison as a rock mass analogue.

6.The effect of confinement on the rock mass modulus

Five rectangular models of 7 m side length(REV size)extracted from different locations of the DFN master volume are employed in order to investigate the effect of confining stress(σ3)on the Young’s modulus during biaxial compression test simulations.At each biaxial simulation,the sample was loaded hydrostatically before the top and bottom platens move toward each other with velocities of 0.02 m/s to induce compressive stress on the body of the specimen.

The Young’s moduli of the 7 m SRM models as a function of confinement are plotted in Fig.23.As shown in the figure,the Young’s modulus of the synthesized rock mass is strongly confinement-dependent.The rock mass modulus increases with increasing confinement and reaches an asymptotic value or plateau beyond the confining stress of about 10 MPa.The maximum rock mass modulus at high confining stresses(i.e.σ3=10 MPa)is approximately between 80%and 90%of the unconfined modulus of the intact rock.For confining stresses greater than 10 MPa,most of the joints are closed and have reached their ultimate normal stiffness value,and as a result,the stiffness of the jointed system is mainly governed by the deformability of the intact rock.The increase in the Young’s modulus of the rock mass with increasing confinement is more pronounced at low confining stresses(σ3≤ 4 MPa).Rosengren and Jaeger(1968),Martin(1997),and Arzúa et al.(2014)observed a similar behaviour on heated Wombeyan marble,damaged LdB granite,and Blanco Mera granite,respectively(Bahrani,2015).

Fig.22.The effect of areal fracture intensity P21on the unconfined rock mass modulus of fractured rock masses.The effect of large-scale structures within the rock is highlighted by using unconfined compression data of the LdB granite representing the peak modulus of the rock,modulus results obtained from the SRM of the joint conditions of the Brockville site,and DEM results for a highly fractured rock as reported in Min and Jing(2004).

Fig.21.The DFN models generated based on field data from(a)the Brockville Tunnel(this study)with three intersecting joint sets(Set 1-red,Set 2-blue,and Set 3-red),and(b)the Sellafield site,Cumbria,UK(Farahmand et al.,2015).

Min and Jing(2004)studied the effect of increasing confining stress on the modulus of a highly jointed granitic rock mass(known as Sella field rock mass)using DEM modelling.The obtained Young’s moduli of the rock mass,as a function of confinement,are plotted in Fig.23.In examining the results for both rock masses,it was found that generally the stiffness of the jointed system increases as a function of confining stress.The trend is consistent with both rock masses displaying a hyperbolic character.Min and Jing(2004)suggested a hyperbolic function to fit the numerical data in the following form:

Fig.23.Confinement-dependency of the Young’s modulus of various intact and jointed rocks under triaxial and biaxial loading conditions for various P21fracture intensity and discontinuity property values.

whereαis defined as a sensitivity parameter with a constant value to fit the obtained numerical results.This formula can be rearranged in the following form:

However,for unconfined loading conditions(σ3=0 MPa),Eq.(4)yields a zero value forErmwhich is not physically meaningful.Therefore,it is suggested to add a parameter in the nominator which is the unconfined rock mass modulusErm,0,i.e.the rock mass modulus atσ3=0 MPa,as shown in the following form:

In the Hoek-Diederichs rock mass modulus equation(Eq.(3)),the Young’s modulus of the jointed rock is a function of the GSI.The GSI value for a specific rock mass is related to the degree of the blockiness and joint condition of the fractured medium.In a similar fashion,we propose that the parameterαis not a constant but a function of the fracture intensityP21and the joint normal stiffnessJknin order to take into account physically meaningful components governing the deformability of a rock mass.The advantage by using these two components is that they can be quantitatively ratherthan qualitatively determined,as direct measurements can be performed.The results of the numerical simulations presented in Fig.23 are used to develop a semi-empirical equation to estimate the confined rock mass modulus.A least square regression analysis was carried out to determine the fitting parameters.The following relationship relates the parameterαwith the modulus of the intact rock(Ei),fracture intensity(P21)and the joint normal stiffness(Jkn):

Fig.24.SEM images of microcrack distributions in thin sections of(a)LdB granite(Lim et al.,2012),and(b)Wombeyan marble(Rosengren and Jaeger,1968).Trace lengths of the microcracks were obtained from the image processing package provided in MATLAB for(c)LdB granite,and(d)Wombeyan marble.

Table 9Summary of the input parameters used in Eq.(6)to evaluate the confinement-dependency of the rock modulus based on the proposed semi-empirical equations(Eqs.(6)-(8)).

wherecis a fitting parameter with a constant value.

Eq.(6)can be used as a means to estimate the confined rock mass modulus in a situation where the normal joint stiffness,areal fracture intensity,and unconfined rock mass modulus are known,based on Eq.(7).Bahrani(2015)used a similar exercise to develop a semi-empirical equation for estimating the confined strength of micro-damaged rocks based on the density of damage for rock specimens.

Initially,in order to validate the proposed semi-empirical equation,three experimental sets of data on laboratory-scale damaged intact rocks were used.The first dataset shown in Fig.23 is based on triaxial laboratory tests on damaged LdB granite specimens reported by Martin(1997).The second and third datasets are based on the results of triaxial testing on heated Wombeyan marble(Gerogiannopoulos,1977)and Blanco Mera granite(Arzúa et al.,2014).As discussed by Rosengren and Jaeger(1968)and Bahrani et al.(2014),damaged intact rock specimens can be assumed to be an analogue to a jointed rock mass.Image processing tools implemented in MATLAB(MathWorks,2016)were used to evaluate fracture intensityP21of the damaged LdB granite and the Wombeyan marble by analysing the microcrack distribution in thin section images of these rocks,as illustrated in Fig.24.The fitting parameters for all the damaged samples,which were derived from the least square analysis,are presented in Table 9.It should be noted that this equation was developed based on numerical results obtained for only two different rock masses.Therefore,it is necessary to test the validity of this equation to a wide range of case studies with various joint intensity values and joint conditions.

In order to evaluate the fit between the results obtained from the proposed equation and the laboratory data,an error analysis approach was employed.The calculated error is defined as the difference between the expected value(semi-empirical equation)and the observed value(numerical and laboratory results).These differences have to be random and unpredictable,and the proposed formula was evaluated by using residual plots in order to ensure the randomness in the calculated error.The residual plots are illustrated in Fig.25 for each case,demonstrating lowmagnitude error values(≤20%)and a randomness in the pattern of the calculated error.The high-magnitude errors observed for the Brockville SRM dataset and the Blanco Mera granite dataset can be attributed to the more anisotropic geometry of the joints present.

Furthermore,by solely using the results obtained from the numerical models,it was observed that the parametercin Eq.(7)can be potentially expressed as the ratio between the initial joint apertureuj,0and the mean joint trace lengthLt.In this case,Eq.(7)can be rearranged into

In order to derive this semi-empirical equation,data originated from the conducted SRM modelling and the DEM modelling of Min and Jing(2004)were used,as all of the parameters implemented in the proposed formula(Eq.(8))are provided in the numerical models.However,for the used laboratory data reported by the aforementioned researchers,critical information including joint aperture and mean joint trace length were not reported;hence the laboratory data were not examined in order to obtain Eq.(8).While Eq.(8)shows that parameterαcould be calculated using quantities that can be measured,further investigations,which are out of the scope of this study,are required in order to ensure the validity of the equation and its wider application.

7.Discussion

As illustrated in Fig.9,the RQD index does not vary with the examined borehole length and it does not appear to be scaledependent.This is based on the values obtained from the“virtual”boreholes employed within the DFN model.The RQD value measured from various virtual core lengths ranges from 95 to 100,indicating that the examined rock mass is slightly to moderately jointed.Furthermore,joint spacing values obtained from the virtual boreholes were fitted to a lognormal distribution with a mean value of 0.6 m.This mean spacing value is used to make a preliminary estimate of the average block volume of the given rock mass.On the other hand,areal fracture intensity and block volume measurement results indicate that these measured quantities depend on the size of the sample being examined.

To determine a range of GSI values for the examined rock mass,three methods based on measuring the RQD,mean joint spacing,and mean block volume were applied to the virtual 3D LiDAR model of the Brockville Tunnel.In the RQD-based method,the rock mass condition was inferred based on the one-dimensional index of RQD and the joint surface condition,while the methods based on joint spacing and block volume quantify the degree of interlocking of the jointed medium on the basis of the measured spacing between discontinuities and the mean volume of blocks,respectively.The degree of blockiness for the GSI estimation(50≤GSI≤67)obtained from the joint spacing and block volume values underestimates the degree of blockiness observed in the Brockville Tunnel where the rock mass conditions clearly indicate that the rock mass is massive to moderately jointed(GSI>65).Quantifying the degree of blockiness based on the RQD seems to give a better estimate of theUCSrm.A GSI range from 67 to 77,estimated according to the measured RQD,corresponds more closely to the field observations made at the site.In Table 10,the quantities examined in order to provide GSI estimates and their respective ranges are summarised.

An upscaling procedure was performed to extract the geometrical properties of the rock mass.The obtained properties at this size are assumed to be representative of the rock mass behaviour at large scale by eliminating associated size effects.To establish the geometrical REV size,the variability of RQD,P21andVbwith increasing sample size was investigated.The geometrical REV size of 7 m is established based on the variability of the aforementioned parameters.An overall REV size of 7 m is determined for the rock mass according to the variability of the geometrical and mechanical properties.The extracted mechanical properties at this scale can be considered as equivalent continuum properties and can be used as input parameters for large-scale modelling of jointed rock masses.In this study,the SRM sample of 7 m length was used to examine the influence of confining stress on the rock mass deformability.

The sensitivity of the Young’s modulus of the rock mass to the confining stress is investigated in Section 6,and as shown in Fig.22,the rock mass modulus in unconfined conditions(Erm,0)is highly affected by the magnitude of fracture intensity(P21).Greater fracture intensity values result in reducing stiffness of the jointed medium,considering the same joint condition based on the normal stiffness(Jkn)assigned to the joints.These results are in agreement with the empirical solution in Eq.(3),in which theErmis reversely proportional to the degree of blockiness of the medium(GSI value).In general,the rock mass modulus is more sensitive to lower values of confining stresses.At high confinement conditions,most of the joints reach their residual aperture,and as a result,the stiffness of the rock mass is no longer affected by increasing the confining stress.Similar trends are observed when the effects of confinement on the Young’s modulus of laboratory samples of LdB granite,Wombeyan marble and Blanco Mera granite were investigated.

With increasing confinement,the rock mass modulus reaches an asymptotic value,and for confining stresses greater than 10 MPa,the rock mass modulus based on the SRM results was between 80%and 90%of the unconfined Young’s modulus of the intact rock,as shown in Fig.23.The results of numerical simulations presented in this paper were used to develop a semi-empirical equation for the estimation of the confined modulus of moderately jointed rock masses.This equation can be used when the normal joint stiffness,areal fracture intensity,and unconfined rock mass modulus are known.The unconfined Young’s modulus of the jointed rock mass can be estimated using currently available empirical equations or by back-analysis of observed rock mass behaviour.Furthermore,based on the presented numerical analysis results,preliminary observations suggest that joint aperture and joint persistence,expressed using the measured mean trace length,could also be implemented in the suggested semi-empirical equation;hence by taking into account the rock mass blockiness,based on fracture intensity and persistence,and the overall joint stiffness,based on the initial joint apertureuj,0and joint stiffnessJkn,the confined rock mass modulus can be estimated.

Furthermore,in both this study(SRM results)and the DEM modelling conducted by Min and Jing(2004),the behaviour of the joint contacts under compressive loading is modelled by using the hyperbolic function suggested by Bandis et al.(1983):

wherekn0,cis the initial normal stiffness of the contact,uis the contact closure under compression,andumaxis the maximum closure(Fig.26).

As observed in Eq.(9),joint closure results in primarily a progressive increase in the stiffness of an independent joint,leading to an increase in the overall stiffness of the jointed medium as all joints start closing.This phenomenon is captured by both the SRM models(this study)and the DEM modelling(Min and Jing,2004),as well as the suggestedsemi-empirical equations(Eqs.(6)-(8)).From the SRM modelling results,it is observed that the closure of the joints at high confinement stresses leads to a stiffer assembly with the modulus of the jointed medium yielding a constant value close to the modulus of the intact rock.Similarly,the semi-empirical equation in this case is asymptotically reaching a constant value,as shown in Fig.23.However,from the DEM modelling results,it can be observed that while there is an increase in the modulus at higher confining stresses,within the investigated stress range,the modulus ratio is not reaching a constant value,as in the previous case.A similar trend can be observed from the predicted modulus ratio based on the suggested semi-empirical equation.This phenomenon can be attributed to the high fracture intensity value that characterises that specific rock mass,which results in an overall‘softer’medium that would require higher confining stresses in order for all joints present to close.

Finally,the proposed hyperbolic equation could also be implemented into continuum-based numerical codes in order to define the confinement-dependent elastic behaviour of materials.It should be noted that this equation was developed based on numerical results obtained for only two different rock masses.Therefore,it is necessary to test the validity of this equation for a wide range of case studies with various joint intensity values and joint surface conditions.

8.Summary and concluding remarks

In this paper,a quantitative procedure for estimating the largescale geometrical properties and their effects on the mechanical properties of moderately jointed rock masses was presented.The impact of the geometrical characteristics on the mechanical properties of a rock mass was examined by employing both empirical and numerical methods.Joint geometrical properties that can be measured either in the field or “virtually”through the use of 3D LiDAR models were used as input parameters for the generation of large-scale 3D DFN models.From the master DFN model,multiple domains with different arrangements of joints(joint density,intensity,persistence,and orientation)were further processed in order to investigate the distribution and variability of the structural characteristics of the rock mass in order to establish the geometrical REV.The variability of the RQD,joint spacing,and block volume at a representative volume was used to quantify the degree of blockiness.The resultant range of GSI estimated from the determined degree of blockiness was used as an input parameter into empirical criteria to predict the rock mass strength and deformability.For the unconfined condition,the rock mass modulus and UCS values predicted by the SRM models were approximately close to the properties estimated by empirical criteria(Difference between the obtained values was estimated at less than 10%).It should be noted that the Hoek-Brown criterion tends to overestimate the strength of moderately/highly interlocked jointed rock under confined condition as reported by Diederichs(2007)and Bahrani and Kaiser(2013).

The sensitivity of the Young’s modulus of the rock mass to the confining stress was also investigated.It has been shown that the rock mass modulus in an unconfined condition(Erm,0)is highly affected by the magnitude of fracture intensity(P21).As expected,greater fracture intensity values result in reducing stiffness of the jointed medium,considering the same joint condition based on the normal stiffness(Jkn)assigned to the joints.These results are in agreement with the empirical Hoek-Diederichs equation(Hoek and Diederichs,2006)in which theErmis reversely proportional to the degree of blockiness of the medium(GSI value).In general,the rock mass modulus is more sensitive to the lower values of confining stresses.At high confinement conditions,most of joints reach their residual aperture,and as a result,the stiffness of the rock mass is no longer affected by increasing the confining stress.Similar trends are observed when the effects of confinement on the Young’s modulus of laboratory samples of LdB granite,Wombeyan marble and Blanco Mera granite were investigated.A semiempirical equation was suggested by fitting a hyperbolic function on the available data demonstrating the relationship between rock mass modulus and applied confinement.

Table 10GSI estimated ranges based on quantitative methods and their examined quantity ranges according to Fig.17.

Fig.26.Behaviour of the fracture contact under pure compressive loading.kn,cdenotes the normal stiffness of the contact.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The authors wish to thank the Nuclear Waste Management Organization(NWMO)of Canada,the National Science and Engineering Research Council(NSERC),the Canadian Ministry of National Defence(DND),and the RMC Green Team for funding this research.The discussions with Dr.Alireza Baghbanan,Dr.Matthew Perras,and Mr.Felipe Duran Del Vale significantly helped with the preparation of this paper.

List of acronyms

CI Crack initiation stress

CD Crack damage stress

CoV Coefficient of variance

DFN Discrete fracture network

LdB Lac du Bonnet

LiDAR Light detection and ranging

GBM Grain based model

GSI Geological strength index

REV Representative elementary volume

RMR Rock mass rating

RMi Rock mass index

RQD Rock quality designation

SRM Synthetic rock mass model

UCS Unconfined compressive strength

List of major symbols

CcPrimary cohesion

Cc,2ndSecondary cohesion

CiCohesion of intact rock

D Disturbance factor

D50The volume at which 50%of the blocks are passing

D60/D10Coefficient of uniformity

D230/（D60D10）Coefficient of gradation

EiYoung’s modulus of intact rock

ErmRock mass modulus

Erm,0Unconfined rock mass modulus

fshShear strength

fresResidual shear strength

GIcFracture energy in Mode I

GIIcFracture energy in Mode I

JknJoint normal stiffness

KFisher constant

kn0,cInitial normal stiffness

ksh0,cInitial shear stiffness

miRock constant of the Hoek-Brown criterion of the

intact rock

P21Areal fracture intensity

SaMean joint spacing

spShear displacement atfsh

sresShear displacement atfres

TiTensile strength of intact rock

TcTensile strength

upCrack opening atTc

uresCrack opening atσn=0

VbBlock volume

viPoisson’s ratio of intact rock

σnNormal stress

φcPrimary friction angle

φc,2ndSecondary friction angle

φiFriction angle of intact rock

Arzúa J,Alejano L,Walton G.Strength and dilation of jointed granite specimens in servo-controlled triaxial tests.International Journal of Rock Mechanics and Mining Sciences 2014;69:93-104.

Backers T.Fracture toughness determination and micromechanics of rock under mode I and mode II loading.PhD Thesis.University of Potsdam;2005.

Baecher GB.Statistical analysis of rock mass fracturing.Mathematical Geology 1983;15(2):329-48.

Bahrani N,Kaiser P.Strength degradation of non-persistently jointed rock mass.International Journal of Rock Mechanics and Mining Sciences 2013;62:28-33.

Bahrani N,Kaiser P,Valley B.Distinct element method simulation of an analogue for a highly interlocked,non-persistently jointed rock mass.International Journal of Rock Mechanics and Mining Sciences 2014;71:117-30.

Bahrani N.Estimation of confined peak strength for highly interlocked jointed rock masses.PhD Thesis.Laurentian University of Sudbury;2015.

Bandis SC,Lumsden AC,Barton NR.Fundamentals of rock joint deformation.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1983;20(6):249-68.

Barton NR,Lien R,Lunde J.Engineering classification of rock masses for the design of tunnel support.Rock Mechanics 1974;6(4):189-239.

Bass J.Elasticity of minerals,glasses,and melts.In:Mineral physics&crystallography:a handbook of physical constants.American Geophysical Union;1995.p.45-63.

Bear J.Dynamics of fluids in porous media.New York:Elsevier;1972.

Bieniawski Z.Rock mass classification in rock engineering.Rotterdam:A.A.Balkema;1976.p.97-106.

Bieniawski ZT.Engineering rock mass classification.New York:Wiley Interscience;1989.

Bonnaffe F,Jennette D,Andrews J.A method for acquiring and processing groundbased lidar data in difficult-to-access outcrop for use in three-dimensional,virtual-reality models.Geosphere 2007;3(6):501-10.

Cacciari PP,Futai MM.Mapping and characterization of rock discontinuities in a tunnel using 3D terrestrial laser scanning.Bulletin of Engineering Geology and the Environment 2016;75:223-37.

Cai M,Kaiser PK,Uno H,Tasaka Y,Minami M.Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system.International Journal of Rock Mechanics and Mining Sciences 2004;41(1):3-19.

Davy P,Le Goc R,Darcel C.A model of fracture nucleation,growth and arrest,and consequences for fracture density and scaling.Journal of Geophysical Research Solid Earth 2013;118:1393-407.

Deere D.Geological consideration.In:Rock mechanics in engineering practice.New York:Wiley;1968.

Dershowitz WS,Einstein HH.Characterizing rockjoint geometry with joint system models.Rock Mechanics and Rock Engineering 1988;21(1):21-51.

Dershowitz WS,Herda HH.Interpretation of fracture spacing and intensity.In:Proceedings of the 32nd US rock mechanics Symposium;1992.p.757-66.

Diederichs M.The 2003 Canadian Geotechnical Colloquium:mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling.Canadian Geotechnical Journal 2007;44(9):1082-116.

Dowd PA,Xu C,Mardia KV,Fowell RJ.A comparison of methods for the stochastic simulation of rock fractures.Mathematical Geology 2007;39:697-714.

Esmaieli K,Hadjigeorgiou J,Grenon M.Estimating geometrical and mechanical REV based on synthetic rock mass models at Brunswick Mine.International Journal of Rock Mechanics&Mining Sciences 2010;47:915-26.

Farahmand K,Baghbanan A,Shahriar K,Diederichs M.Effect of fracture dilation angle on stress-dependent permeability tensor of fractured rock.In:Proceedings of the 49th US rock mechanics Symposium;2015.

Farahmand K,Diederichs M.A calibrated synthetic rock mass(SRM)model for simulating crack growth in granitic rock considering grain scale heterogeneity of polycrystalline rock.In:Proceedings of the 49th US rock mechanics Symposium;2015.

Farahmand K.Characterization of rock mass properties and excavation damage zone(EDZ)using a synthetic rock mass(SRM)approach.PhD Thesis.Kingston,Canada:Queen’s University;2017.

Fardin N,Feng Q,Stephansson O.Application of a new in situ 3D laser scanner to study the scale effect on the rock joint surface roughness.International Journal of Rock Mechanics and Mining Sciences 2004;41:329-35.

Fekete S,Diederichs MS,Lato MJ.Geotechnical and operational applications for 3-dimensional laser scanning in drill and blast tunnels.Tunneling and Underground Space Technology 2010;25(5):614-28.

Feng QH,Roshoff K.In-situ mapping and documentation of rock faces using a fullcoverage 3D laser scanning technique.International Journal of Rock Mechanics and Mining Sciences 2004;41:139-44.

Gerogiannopoulos N.A critical state approach to rock mechanics.PhD Thesis.London:Imperial College London(University of London);1977.

Hamdi P,Stead D,Elmo D.Characterizing the influence of stress-induced microcracks on the laboratory strength and fracture development in brittle rocks using a finite-discrete element method-micro discrete fracture network FDEM-mDFN approach.Journal of Rock Mechanics and Geotechnical Engineering 2015;7(6):609-25.

Haneberg WC.Using close range terrestrial digital photogrammetry for 3-D rock slope modeling and discontinuity mapping in the United States.Bulletin of Engineering Geology and the Environment 2008;67(4):457-69.

Hoek E,Carlos CT,Brent C.Hoek-Brown failure criterion-2002 Edition.In:Proceedings of the NARMS-TAC Conference;2002.p.267-73.

Hoek E,Carter TG,Diederichs MS.Quantification of the geological strength index chart.In:Proceedings of the 47th US rock mechanics/geomechanics Symposium.American Rock Mechanics Association;2013.

Hoek E,Diederichs MS.Empirical estimation of rock mass modulus.International Journal of Rock Mechanics and Mining Sciences 2006;43(2):203-15.

Hoek E,Marinos P,Benissi M.Applicability of the geological strength index(GSI)classification for very weak and sheared rock masses:the case of Athens Schist Formation.Bulletin of Engineering Geology and the Environment 1998;57(2):151-60.

Hudson JA,Harrison JP.Engineering rock mechanics.Oxford:Elsevier;1997.

Hutchinson DJ,Diederichs MS.Cablebolting in underground mines.Bitech Publishers Ltd;1996.

Innovmetric.Polyworks V 11.0.4.Quebec City:Innovmetric;2016.

ISRM.Commision on standardization of laboratory and field tests:suggested methods for the quantitative description of discontinuities in rock masses.International Journal of Rock Mechanics and Mining Sciences 1978;15(6):319-68.

Itasca.3DEC,ver.5.0.Minneapolis,USA:Itasca Consulting Group,Inc.;2013.

Itasca.The Universal distinct element code(UDEC),ver.6.0.Minneapolis,USA:Itasca Consulting Group,Inc.;2014.

Lato MJ,Diederichs MS,Hutchinson DJ.Bias correction for view-limited lidar scanning of rock outcrops for structural characterization.Rock Mechanics and Rock Engineering 2010;43(5):615-8.

Lato MJ,Voge M.Automated mapping of rock discontinuities in 3D lidar and photogrammetry models.International Journal of Rock Mechanics and Mining Sciences 2012;54:150-8.

Lim SS,Martin CD,Åkesson U.In-situ stress and microcracking in granite cores with depth.Engineering Geology 2012;147:1-13.

Mahabadi O,Randall N,Zong Z,Grasselli G.A novel approach for microscale characterization and modeling of geomaterials incorporating actual material heterogeneity.Geophysical Research Letters 2012;39(1).https://doi.org/10.1029/2011GL050411.

Martin C.The strength of massive Lac du Bonnet granite around underground openings.PhD Thesis.Winnipeg,Canada:University of Manitoba;1993.

Martin C.Seventeenth Canadian geotechnical colloquium:the effect of cohesion loss and stress path on brittle rock strength.Canadian Geotechnical Journal 1997;34(5):698-725.

MathWorks.MATLAB R2016b.Natick,Massachusetts,United States:The Math-Works,Inc;2016.

Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis of porous media.Cambridge University Press;2009.

Mills G,Fotopoulos G.On the estimation of geological surface roughness from terrestrial laser scanner point clouds.Geosphere 2013;9(5):1410-6.

Min K,Jing L.Stress dependent mechanical properties and bounds of Poisson’s ratio for fractured rock masses investigated by a DFN-DEM technique.International Journal of Rock Mechanics and Mining Sciences 2004;41:390-5.

Mirarco.MoFrac software version alpha.Mirarco Mining Innovation.2015.http://www.mofrac.com.

Nirex.Evaluation of heterogeneity and scaling of fractures in the borrowdale Volcanic Group in the Sellafield area.Technical report SA/97/028.Harwell,UK:Nirex;1997.

Noorian Bidgoli M,Zhao Z,Jing L.Numerical evaluation of strength and deformability of fractured rocks.Journal of Rock Mechanics and Geotechnical Engineering 2013;5(6):419-30.

Palmstrom A.Measurements of and correlations between block size and rock quality designation(RQD).Tunnelling and Underground Space Technology 2005;20(4):362-77.

Palmstrom A.Characterizing rock masses by the RMi for use in practical rock engineering,Part 1:the development of the rock mass index(RMi).Tunnelling and Underground Space Technology 1996;11(2):175-88.

Rocscience.DIPS.Toronto:Rocscience Inc.;2006.

Rosengren KJ,Jaeger JC.The mechanical properties of an interlocked low-porosity aggregate.Géotechnique 1968;18(3):317-26.

Schultz R.Limits on strength and deformation properties of jointed basaltic rock masses.Rock Mechanics and Rock Engineering 1995;28(1):1-15.

Snow D.Rock fracture spacings,openings,and porosities.Journal of Soil Mechanics and Foundations Division 1968;94(1):73-92.

Srivastava RM.Field verification of a geostatistical method for simulating fracture network models.In:Proceedings of the 41st US rock mechanics Symposium;2006.

Sturzenegger M,Stead D.Close-range terrestrial digital photogrammetry and terrestrial laser scanning for discontinuity characterization on rock cuts.Engineering Geology 2009a;106:163-82.

Sturzenegger M,Stead D.Quantifying discontinuity orientation and persistence on high mountain rock slopes and large landslides using terrestrial remote sensing techniques.Natural Hazards and Earth System Sciences 2009b;9(2):267-87.

Vazaios I,Vlachopoulos N,Diederichs MS.Integration of lidar-based structural input and discrete fracture network generation for underground applications.Geological and Geotechnical Engineering 2017;35(5):2227-51.

Voge M,Lato MJ,Diederichs MS.Automated rock mass discontinuity mapping from 3-dimensional surface data.Engineering Geology 2013;164:155-62.

Watkins H,Bond CE,Healy D,Butler RW.Appraisal of fracture sampling methods and a new work flow to characterise heterogeneous fracture networks at outcrop.Journal of Structural Geology 2015;72:67-82.

Xu C,Dowd P.A new computer code for discrete fracture network modelling.Computers and Geosciences 2010;36:292-301.

Xu C,Dowd PA.Stochastic fracture propagation modelling for enhanced geothermal systems.Mathematical Geosciences 2014;46:665-90.