夹芯复合板柱面成形的数值模拟及试验
梁晓波,蔡中义,高鹏飞
(1.吉林大学 辊锻工艺研究所,长春 130022;2.吉林大学 材料科学与工程学院,长春 130022)
0 引 言
夹芯复合板包括泡沫夹芯夹层板、波纹板夹芯夹层板、桁架夹芯夹层板以及蜂窝夹芯夹层板等,夹芯复合板由于其特殊的结构设计,具有结构轻量化、比强度高、比刚度高、抗震、隔音及选材灵活性大等优点,已在民用、航空航天以及建筑等领域得到广泛应用。近年来,飞机机身、火箭箭体、雷达罩和舱盖以及太阳能收集装置、射电望远镜及各种用途天线的反射面等制造领域,对夹芯复合板曲面有很大需求,然而夹芯复合板尚无成熟的曲面成形技术,这严重制约了其应用。
目前关于夹芯板制备方面的研究比较多,其主要制备方法为真空环境下粘结固化,这种夹芯板的力学性能受粘结剂的制约,易于脱胶和老化,极大地缩小了夹芯板应用领域。焊接夹芯复合板实现接头的冶金连接,具备更优异的力学性能。相关的理论研究主要集中在夹层板弹性变形理论[1-3]、振动和稳定性[4,5]、动力响应等方面[6-8]。在夹芯板的弯曲方面,Peng等[9]研究了钎焊蜂窝板三点弯曲的典型失效模式,分析了不同面板和夹芯厚度对弯曲性能的影响。Seong等[10]从面板厚度、夹芯单元尺寸、初始缺陷尺寸等方面研究了蜂窝板的强度和变形行为。然而关于焊接夹芯板直接曲面成形方面的研究至今鲜有报道。
双向梯形夹芯板是新型的全金属焊接结构复合板,其夹芯为面内两个垂直方向上梯形凸凹波纹交错排列的铝合金板,改善了传统金属夹芯不连续的缺点,使其具有优异的抵抗不同方向变形的能力。本文对双向梯形夹芯复合板柱面成形进行数值模拟,研究其成形特点及成形规律,并通过试验验证其准确性。
1 双向梯形夹芯复合板
双向梯形夹芯板采用钎焊将上、下面板与中间双向梯形芯板焊接而成,如图1(a)所示。上、下面板均选用5050-0铝合金,夹芯为5083铝合金板材冲压而成的正交分布梯形凸、凹台的双向梯形结构板。图1(b)为夹芯的胞元,由1个梯形凹台、4个1/4梯形凹台及4个1/2梯形凸台组成,梯形凸台与凹台通过梯形斜平面连接,斜平面之间由四边形曲面过渡。梯形凸台的上表面U1、U2、U3、U4分别与上面板焊接;梯形凹台的下表面D1、D2、D3、D4、D5分别与下面板焊接。胞元长度方向记为l方向,宽度方向记为w方向,l向斜面与上表面的夹角为α,w向斜面与表面的夹角为β;hc为夹蕊的高度。胞元的主要尺寸参数为:长度l=47 mm、宽度w=47 mm,梯形凹台在l方向的上口宽度l1=24 mm、下底宽度l2=8 mm,在w方向的上口宽度w1=39 mm、下底宽度w2=23 mm。夹芯板的面板材料和芯板材料的力学性能参数如表1所示。

图1 双向梯形夹芯板及其胞元结构Fig.1 Bi-directional trapezoidal sandwich plate and cell structure
图1所示的坐标轴z向为夹芯板厚向;x向为夹芯板成形件的轴线方向;y向为成形件的弯曲方向。夹芯中胞元的w向与坐标轴x向一致,胞元的l方向与坐标轴y向一致。
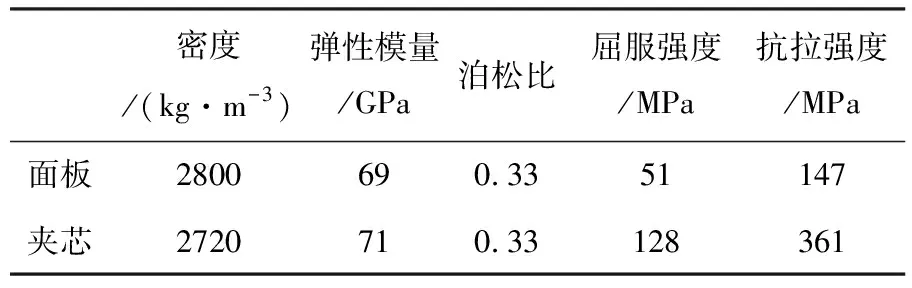
表1 材料力学性能Table 1 Mechanical properties of materials
2 夹芯板成形的数值模拟
采用有限元软件ABAQUS对夹芯复合板圆柱面成形过程进行数值模拟分析。上、下面板厚度tf1、tf2分别为1.5 mm和1 mm,夹芯板料尺寸为330 mm×94 mm,柱面成形件半径R为500 mm。夹芯复合板的上、下面板均划分为六面体网格单元,图2为有限元模型。
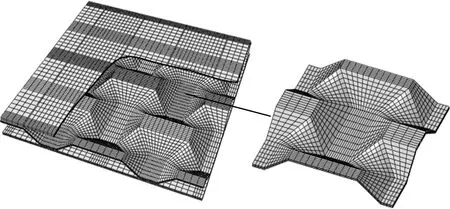
图2 夹芯板及胞元有限元模型Fig.2 FE model of sandwich panel and a unit cell
2.1 面板的变形及应力
图3为成形半径为500 mm的柱面件纵向截面上y方向应变分布。由图可以看到:在柱面成形过程中,上面板受压,下面板受拉,且面板焊接区域的应变明显小于悬空区(非焊接区),这是由面板与芯板焊接使得焊接区域材料变厚造成的。上、下面板在焊接区的应变仅有悬空区的15.2%和11.5%。表明夹芯板柱面弯曲时,受压面板的悬空区相比于焊接区更加容易产生失稳。

图3 截面上y向应变分布Fig.3 Strain distribution of section in y-direction
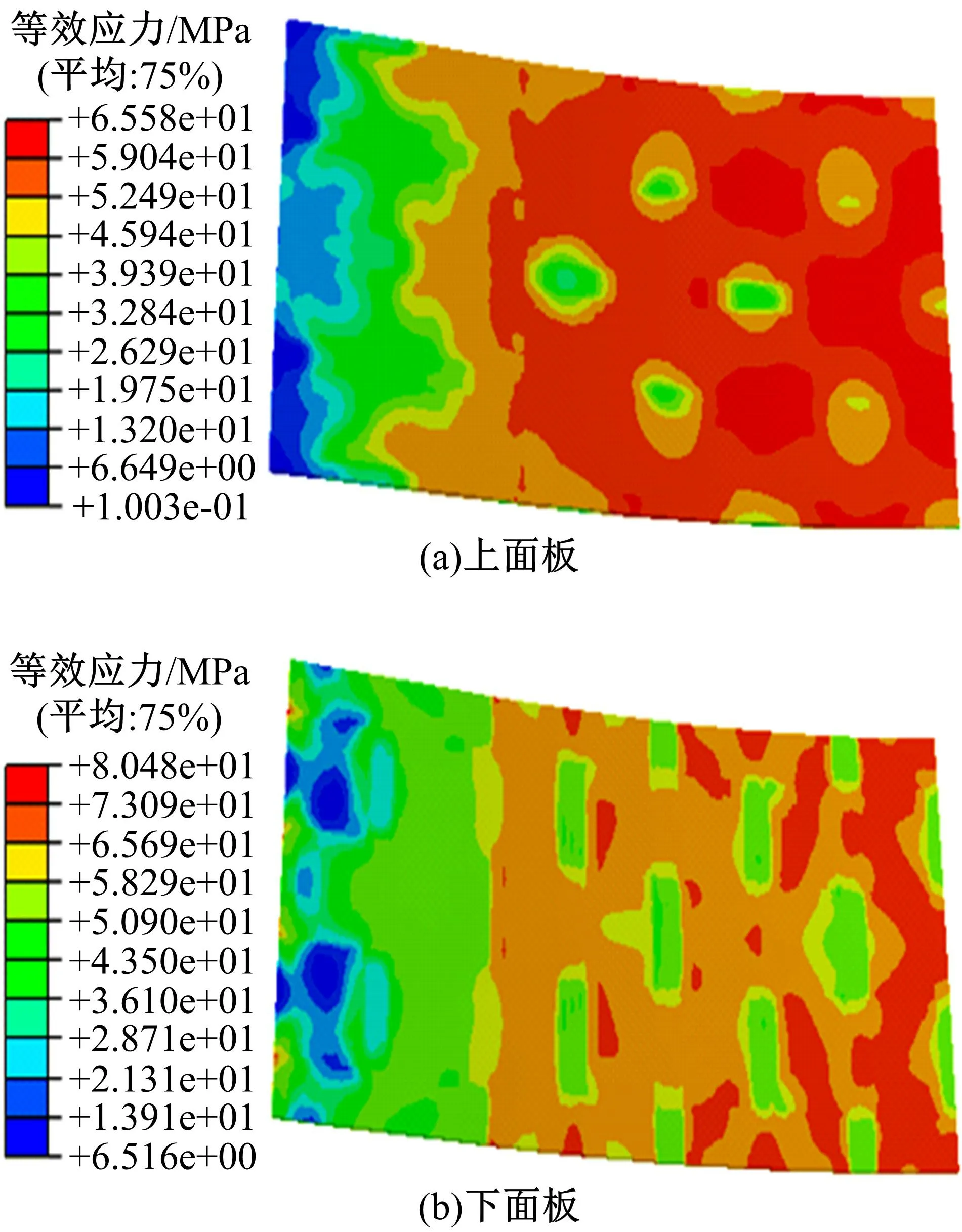
图4 夹芯板柱面的等效应力分布Fig.4 Equivalent stress distribution of cylindrical face sheet
图4为柱面成形件的面板在y向上从对称中心到边缘的等效应力分布。由图可见:上、下面板的应力分布趋势基本一致,从边缘至对称中心线应力逐渐增大。上、下面板的应力分布受面板和夹芯的焊接位置的影响很大,面板悬空区(非焊接区)的应力明显大于面板焊接区域的应力,且悬空区与焊接区的应力差值随柱面曲率半径减小而增大。在面板的中心区域,上、下面板焊接区的等效应力约为悬空区的76.2%和67%;但是靠近面板边缘位置,两种区域的等效应力没有明显差别。
2.2 芯板的变形及应力
图5为芯板的等效应力及等效应变分布。由图可见:在柱面弯曲成形时,夹芯的变形较为复杂,各斜平面间过渡曲面的应变比较大,最大值可达到0.92%;而梯形凸、凹台的底面(即与上、下面板焊接的区域)变形较小。夹芯板成形前后,夹芯胞元y向凸台底面与斜面的夹角α从144.53°变成145.14°,其斜面长度方向的平均应变为6×10-4;x向的夹角β从144.53°变成144.54°,斜面长度方向平均应变为1.9×10-3,表明双向梯形夹芯在弯曲成形时,沿弯曲方向(y方向)上夹芯斜平面的长度几乎没有变化,夹芯的弯曲变形主要通过斜面与底面的夹角变化而完成。

图5 夹芯的等效应力与应变Fig.5 Equivalent stress and strain of core plate

图6 芯板胞元的应力Fig.6 Stress distribution of core plate cell
图6为柱面成形件夹芯胞元的应力分布。由图可见,胞元不仅在柱面弯曲方向(y向)存在较大的正应力σy,在轴线方向(x向)也存在较大的正应力σx,此外还有较小的面内剪应力τxy。同样可见,过渡曲面区域的各个应力分量值都高于其他区域,且分量σx数量级与σy相当,这也从应力分布的角度说明胞元的变形集中在过渡曲面区域。
3 成形缺陷及成形质量影响分析
3.1 夹芯板柱面的成形缺陷
数值模拟结果表明,在夹芯板柱面成形过程中,随着柱面曲率半径的减小,在夹芯板的面板上主要产生3种形式的成形缺陷:凹陷缺陷、局部直面效应以及折皱缺陷。
凹陷缺陷最易发生在面板的悬空区(非焊接区)。当夹芯板沿着夹芯的l方向弯曲时,在受压侧的面板上产生凹陷缺陷,凹陷缺陷数值模拟结果的光照图及其截面线如图7所示。凹陷的原因是受压面板在悬空区发生失稳,轻微的凹陷会使夹芯板成形件的平滑度和表面质量下降,曲面夹芯板在制造过程中要防止较大的凹陷发生。
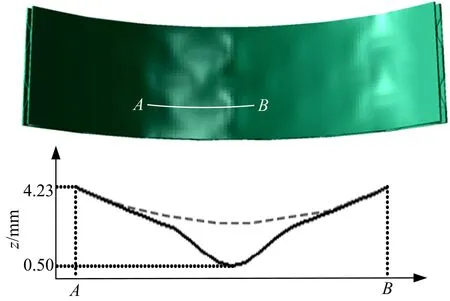
图7 上面板的凹陷成形缺陷Fig.7 Depression forming defects on upper face sheet
局部直面效应数值模拟结果的光照图和截面线如图8所示。局部直面效应同样产生于面板的悬空区,当夹芯板沿着夹芯的l方向弯曲时,在受拉侧的面板上出现局部直面效应。其产生的原因是夹芯板在弯曲成形时产生的拉力只会使面板的悬空区发生伸长变形而不会发生弯曲变形,细微的局部直面效应会使成形件的表面平滑度下降,而局部直面效应较为明显时就成为缺陷,应予以避免。
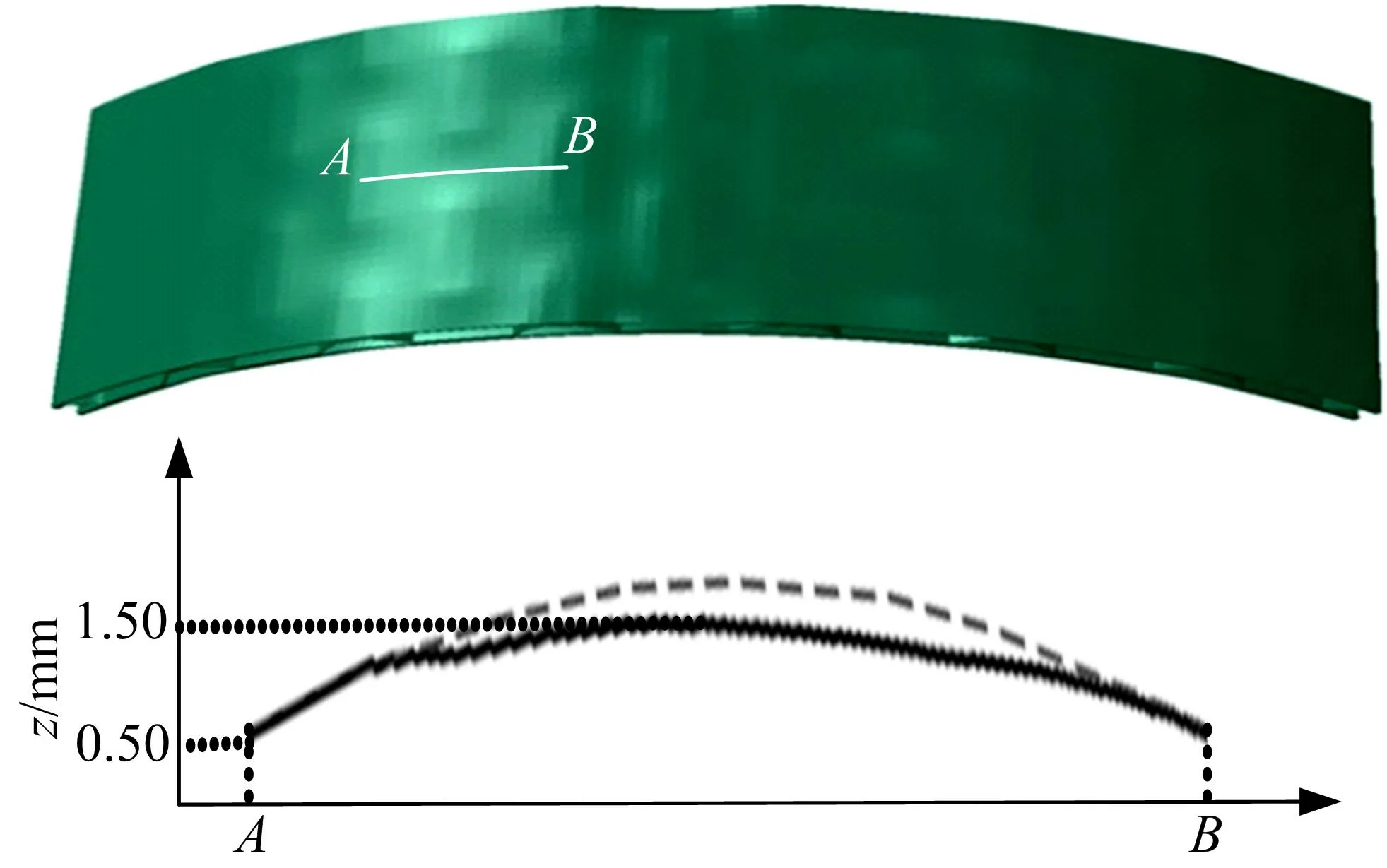
图8 下面板的局部直面成形效应Fig.8 Straight plane forming defects on the lower face sheet
折皱缺陷同样发生在夹芯板受压一侧的面板上,是当夹芯板沿着夹芯的w方向弯曲时,受压面板沿x方向产生贯穿失稳皱曲的一种缺陷,且面板厚度越小越容易产生折皱,折皱缺陷数值模拟结果的光照图和截面线如图9所示。夹芯板曲面成形中折皱的产生会导致成形件报废,成形时应防止其发生。
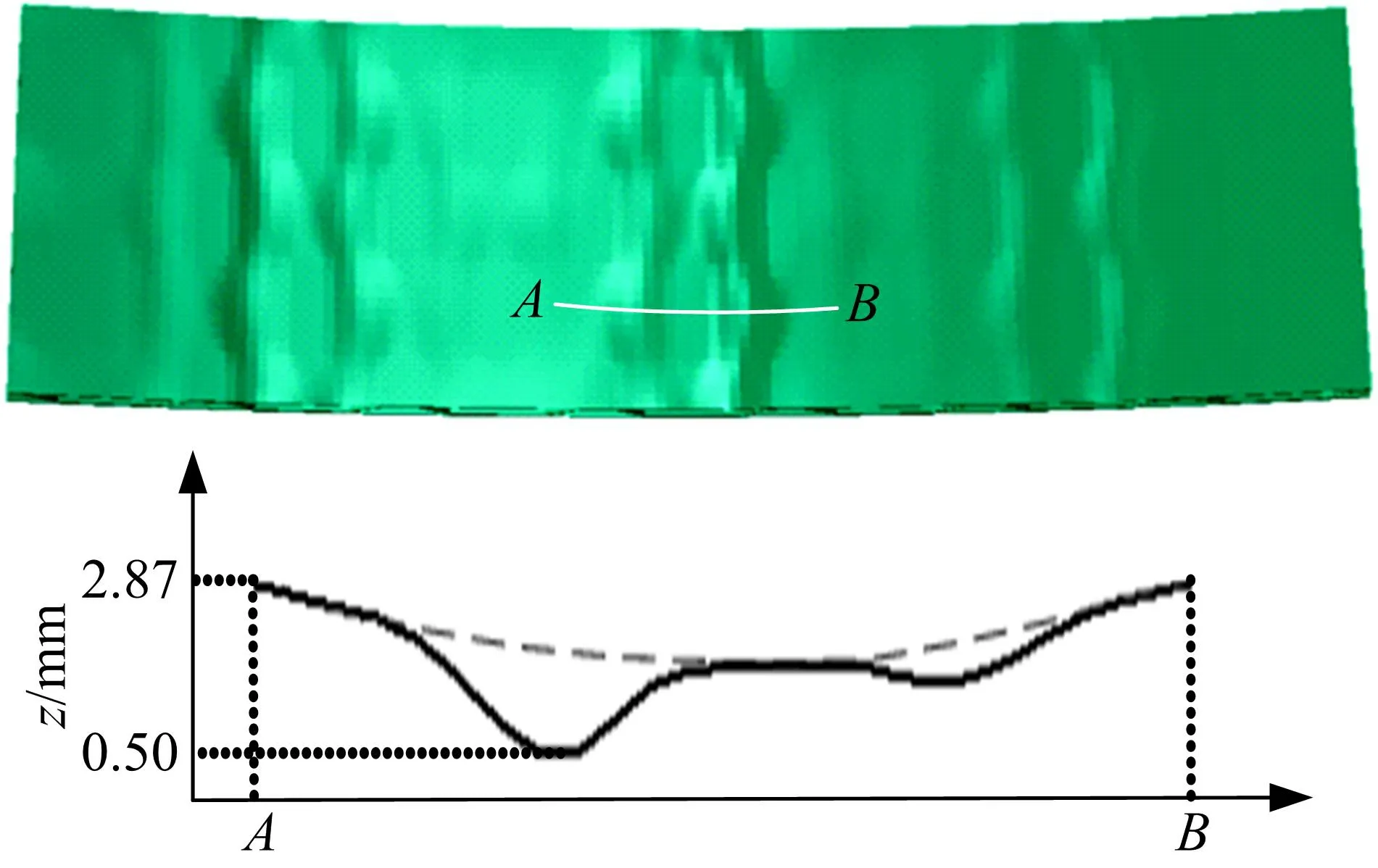
图9 上面板折皱缺陷Fig.9 Wrinkle forming defects on the upper face sheet
3.2 成形质量分析
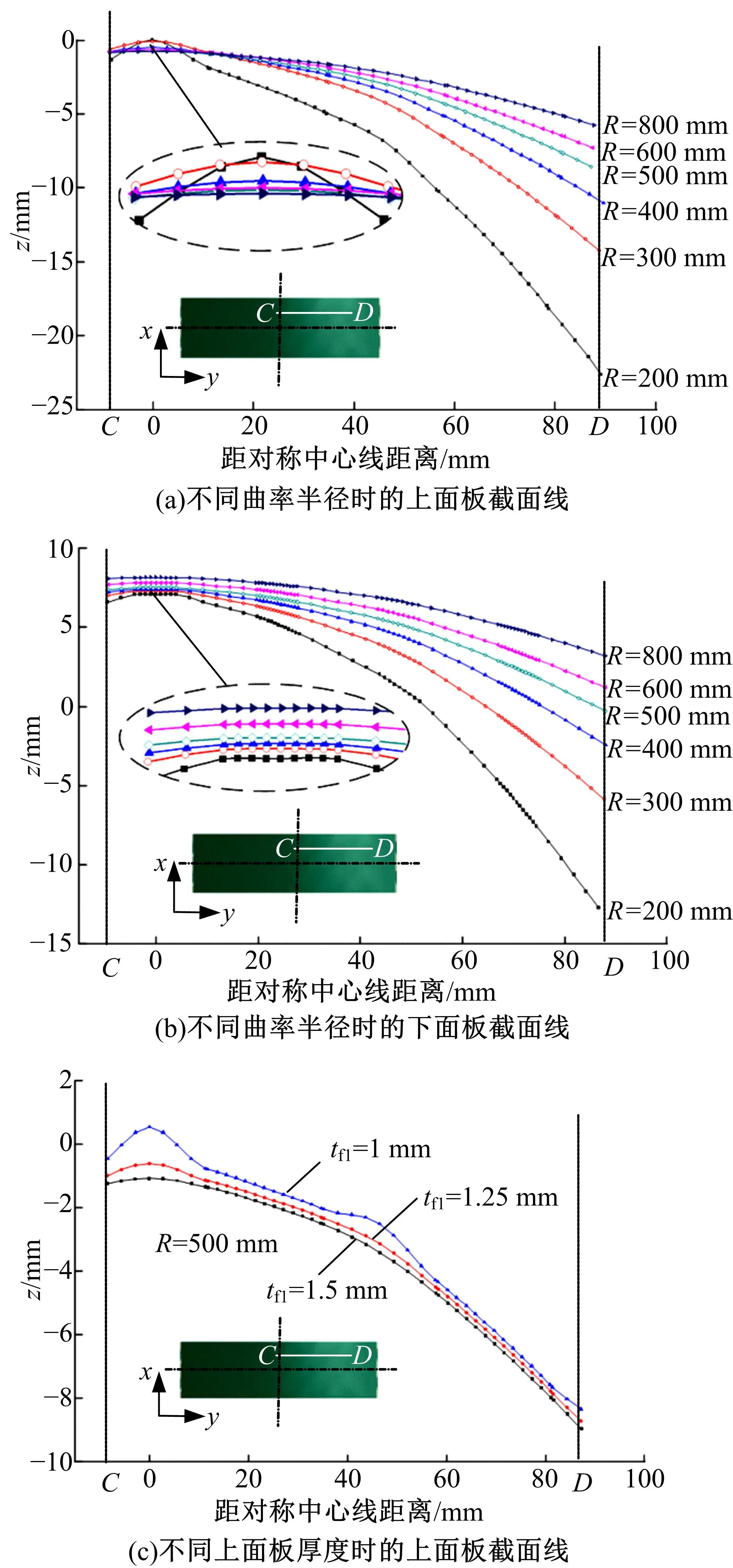
图10 平滑度及成形缺陷随柱面半径及面板厚度的变化Fig.10 Variation of smoothness and forming defects with cylinder radius and thickness of panel
图10为夹芯板不同弯曲半径和面板厚度的柱面纵向截面线,由图可观察柱面件的成形缺陷及平滑度的变化。图中CD截面线经过面板x向对称中心上方23 mm处的一个悬空区的中心,C、D两点分别位于y向对称中心线左侧10 mm和右侧87 mm。图10(a)为tf1=1.5 mm,tf2=1 mm时的上面板截面线,可以看到,半径为200 mm的柱面中心出现了严重的凹陷,半径为400 mm的柱面仅有微小的凹陷,当柱面半径R≥500 mm时,凹陷基本完全消失,表明成形半径越大,面板平滑度越好。下面板的截面线如图10(b)所示,由图可见,半径为200 mm时下面板的悬空区产生了显著的直面效应缺陷,但随着曲率半径的增大,这种缺陷渐渐消失,下面板平滑度逐步提高。图10(c)为柱面半径为500 mm,上面板厚度分别为1、1.25、1.5 mm时的截面线,可以看到,面板凹陷程度随着面板厚度的增大而逐渐减轻,当厚度大于1.5 mm时凹陷逐渐消失。综上所述,夹芯复合板面板厚度和变形程度是影响成形质量的主要因素。
4 夹芯板柱面成形试验
利用多点成形压机对夹芯复合板进行柱面成形试验。通过计算机控制系统调整离散基本体高度构成目标模具型面,将夹芯板成形为不同曲率半径的柱面件。图11为多点压机柱面成形试验。

图11 多点压机柱面成形试验Fig.11 Multi-point pressure forming experiment
图12为不同柱面半径及面板厚度的试验件形貌图。图12(a)给出了tf1=1.5 mm,成形半径分别为500、600、800 mm柱面件,可以看到试验件上面板表面光滑,成形质量比较好。面板厚度对成形缺陷有重要影响,当上面板厚度tf1=1 mm时,成形半径为800 mm的柱面即出现折皱,如图12(b)的数值模拟及试验结果所示,可明显看出其上面板的折痕,且发生在弯曲方向的中心处及左右对称四分之一处。

图12 试验件形貌Fig.12 Morphology of experimental parts
采用三维光学扫描仪对试验件的成形精度进行测量。图13给出了试验件扫描点云以及上面板厚度为1.5 mm、柱面半径分别为500 mm、800 mm时成形件上面板右半侧y向中心截面线的目标值、数值模拟结果以及试验测量值。通过对比得到,夹芯板弯曲半径R=500 mm时的数值模拟值与目标值误差小于2 mm,90%以上截面线误差在0.9 mm以内,而模拟值与测量值基本重合,靠近边缘区域误差稍微增大,最大误差仅为0.6 mm;R=800 mm时的数值模拟值与目标值误差小于2.3 mm,90%以上在1.4 mm以内,而模拟值与测量值的最大误差为1.6 mm。
图14给出了R=500 mm的柱面试验件在中间位置4个胞元的曲率半径测量结果。图中取距x向对称中心线23 mm的y向截面,b1~b5对应上面板胞元悬空区中心点,B1~B4对应焊接区中心点,下面板与之相反。可以看出,曲率半径的分布明显呈现出与夹芯胞元对应的周期性变化。上面板焊接区(B处)比悬空区(b处)的曲率半径偏大,下面板焊接区(b处)比悬空区(B处)的半径偏小,从曲率分布的角度验证了上面板凹陷和下面板直面效应等缺陷。
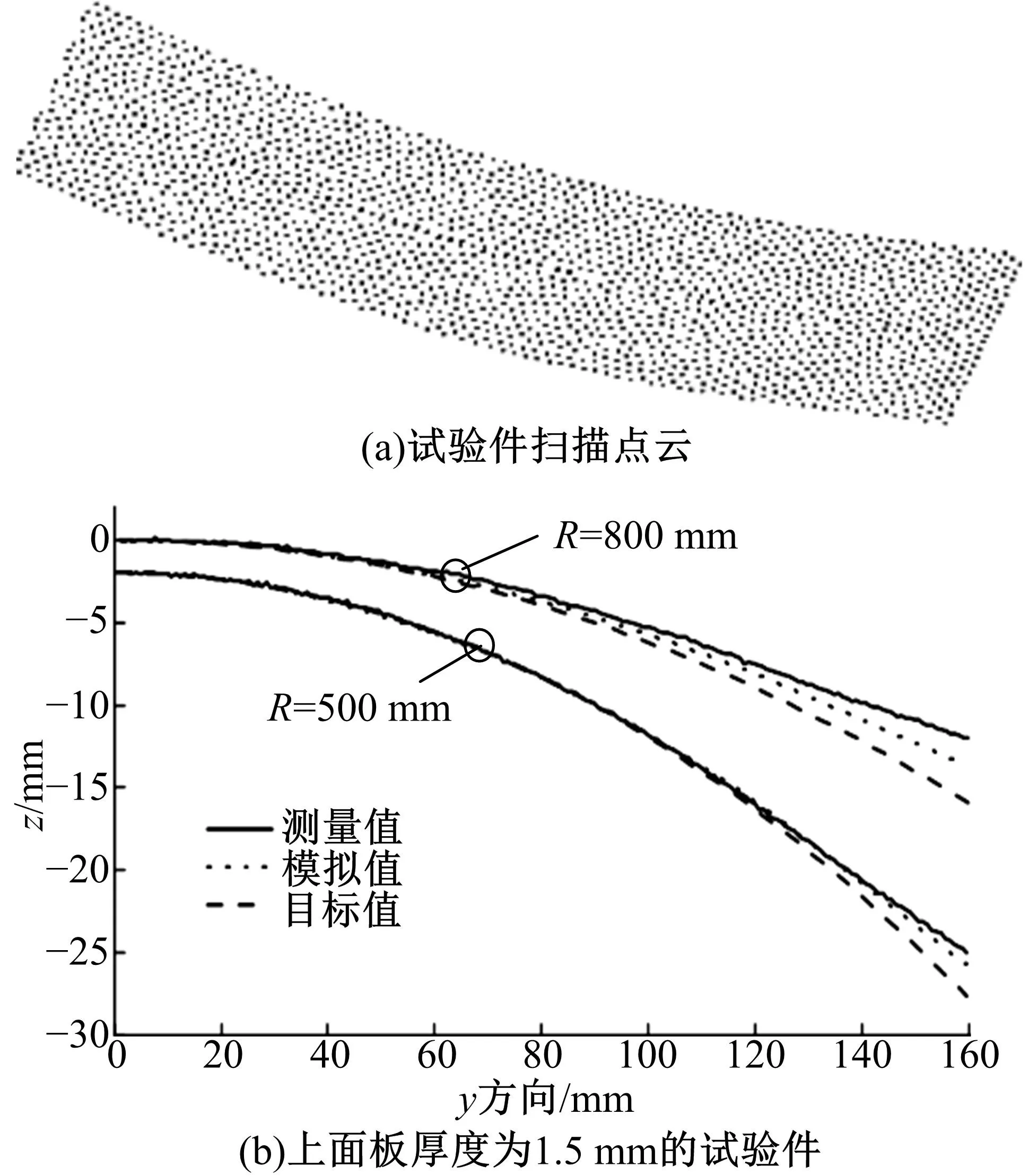
图13 成形件扫描点云及沿y向截面线轮廓Fig.13 Scanning point cloud and profile along y section
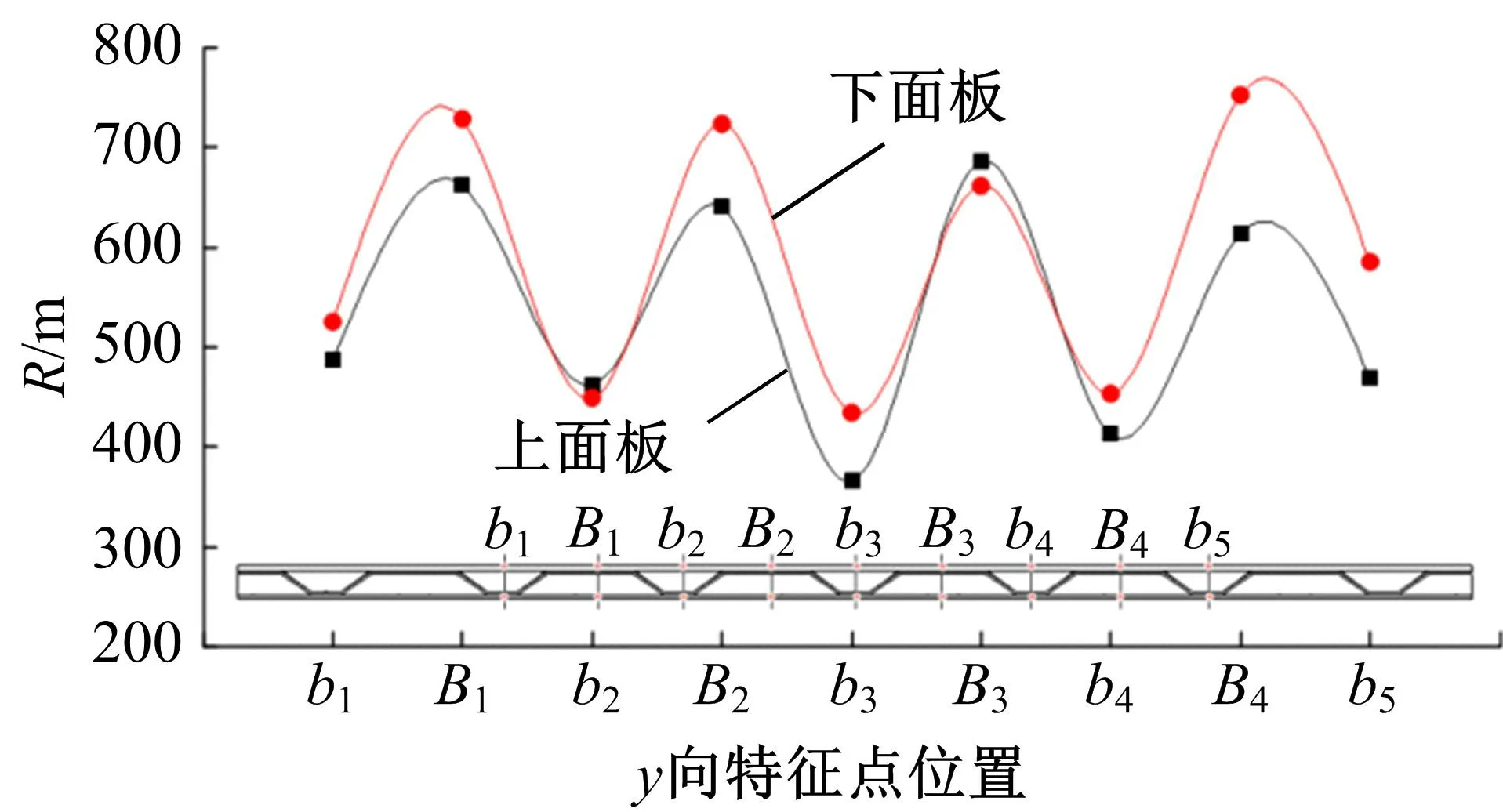
图14 面板特征点处曲率半径Fig.14 Radius at characteristic points of panel
5 结 论
(1)双向梯形夹芯复合板在柱面弯曲成形过程中,上面板受压,下面板受拉,面板悬空区(非焊接区)的应力和应变明显大于焊接区。在柱面中心区域,上面板沿弯曲方向焊接区的应变仅为悬空区的15.2%,等效应力为76.2%;下面板焊接区的应变只有悬空区的11.5%,等效应力只有67%。表明对夹芯板弯曲成形时,面板的悬空区比焊接区更容易出现失稳。
(2)夹芯的弯曲变形主要通过斜面与底面的夹角变化来实现,且夹芯各胞元的变形主要集中在过渡曲面区域。
(3)夹芯板柱面成形过程中,主要出现面板凹陷、面板局部直面效应和面板折皱3种形式的成形缺陷,面板厚度和变形程度是影响成形质量的主要因素。
(4)通过对多点柱面成形试验件形貌、精度以及曲率半径的分析,验证了上文所述夹芯板的成形特点和成形缺陷。
参考文献:
[1] 邓宗白,马超,李栋栋,等. 基于Reissner理论的硬夹心夹层板的弯曲研究[J]. 中国科学:技术科学, 2014(1):81-88.
Deng Zong-bai, Ma Chao, Li Dong-dong, et al. Study on bending of hard core sandwich plates based on Reissner's sandwich theory[J]. Science China Technological Sciences,2014(1):81-88.
[2] Maturi D A, Ferreira A J M, Zenkour A M, et al. Analysis of sandwich plates with a new layerwise formulation[J]. Composites Part B Engineering,2014,56(1):484-489.
[3] Thai H T,Nguyen T K,Vo T P,et al. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory[J]. European Journal of Mechanics—A/Solids,2014,45(2):211-225.
[4] Lok T S, Cheng Q H. Bending and forced vibration response of a clamped orthotropic thick plate and sandwich panel[J]. Journal of Sound & Vibration,2001,245(1):63-78.
[5] Swaminathan K, Naveenkumar D T. Higher order refined computational models for the stability analysis of FGM plates-analytical solutions[J]. European Journal of Mechanics—A/Solids,2014,47(12):349-361.
[6] 刘人怀,成振强. 简支夹层矩形板的非线性弯曲[J]. 应用数学和力学,1993,14(3):203-218.
Liu Ren-huai,Cheng Zhen-qiang. Nonlinear bending of simply supported rectangular sandwich plates[J]. Applied Mathematics and Mechanics,1993,14(3):203-218.
[7] Zenkour A M. A comprehensive analysis of functionally graded sandwich plates: Part 1—Deflection and stresses[J]. International Journal of Solids & Structures,2005,42(18):5224-5242.
[8] Khalili S M R,Kheirikhah M M,Fard K M. Biaxial wrinkling analysis of composite-faced sandwich plates with soft core using improved high-order theory[J]. European Journal of Mechanics—A/Solids,2014,43(43):68-77.
[9] Peng M J,Sun Y,Yao J,et al. Finite element simulation on three-point bending of brazed aluminum honeycomb panel[J]. Advanced Materials Research,2010,168-170:1046-1050.
[10] Seong D Y,Yang D Y,Nam G H,et al. Bending behaviors of metallic sandwich plates with a sheared dimple core under simply supported loading[J]. Journal of Sandwich Structures & Materials,2011,13(4):445-466.

