冰雪条件下快速路汇流区可变限速控制

陈永恒，刘鑫山，熊 帅，汪昆维，谌 垚, 杨少辉

(1.吉林大学 交通学院，长春 130022；2.中国城市规划设计研究院 城市交通研究分院，北京100037)

0 引 言

中国北方地区冬季漫长、降雪量大，不仅影响驾驶员的视野及心理，而且容易引起路面结冰的现象，导致车辆行驶安全性降低，使得本来就相对敏感的快速路交通更不稳定，尤其是当交通需求较大时，更容易形成大面积、长距离的拥堵，而拥堵的消散过程又更为缓慢，给国民经济的发展带来了巨大损失。

长期以来，国内外学者对冰雪条件下的城市快速路做了大量研究，并取得了一定的成果。在冰雪条件对驾驶员的影响方面，邢恩辉等[1]以8名熟练驾驶员为样本，对冰雪对驾驶员感知特性的影响进行了研究，得出冰雪环境下驾驶员视觉感知车速比非冰雪环境下降低了5%～14%，前、后车距离在50 m以内时两种环境下驾驶员视觉感知车距无差异的结论。在冰雪条件对交通流的影响方面，Knapp等[2]通过研究爱荷华州的数据发现，冬季风雪能够使交通量降低16%～47%，并得出交通量的降低量与风速的平方及降雪量成正相关的关系；邢恩辉等[3]通过采集哈尔滨市快速路的数据发现，冰雪条件使自由流速度降低了10 km/h，平均车速降低约20%，且冰雪条件下行车速度随流量增大而降低的速度更快。在冰雪条件下快速路车流控制方面，李松龄等[4]基于车辆追尾条件及跟驰特性建立了各种冰雪条件下城市快速路的限速模型，将在哈尔滨地区采集的数据代入模型中进行计算，得到不同流量下各种冰雪条件的限速值，并给出根据车型与交通量进行分级限速管理的建议。

虽然目前对于城市快速路的研究已取得了大量成果，但已有研究成果多集中在冰雪条件下快速路的交通特性方面以及提高冰雪条件下快速路的行车安全性方面，对于如何提高在冰雪条件下交通需求较大时快速路的行车效率方面则少有涉及。为此，本文在前人研究的基础上，提出了一种以提高冰雪条件下快速路的行车效率为目标的城市快速路可变限速(Variable speed limits,VSL)控制方法，对于冰雪环境下的快速路管理具有一定的参考意义。

1 冰雪对城市快速路交通的影响

冰雪主要通过3个方面的影响来干扰城市快速路的正常运行：①降雪落至路面之后如不及时清理，会因车辆碾压形成压实雪附着在路面上，甚至形成冰板路面，从而交大程度地降低轮胎与路面之间的附着力，降低车辆的爬坡能力及行驶稳定性，进而降低车速，增大交通流运行时的安全车距，降低道路通行能力；②降雪天气直接降低了环境的能见度，使驾驶员的视野变小，视线变得模糊不清；③冰雪天气通过环境的改变增大了驾驶难度，使驾驶员的心理变得急躁、紧张等，进而对相对车速、车间距离等的感知判断能力发生改变。

在研究冰雪条件对道路交通流的影响时，通常将降雪情况和路面情况分为若干级别进行研究。如在《道路通行能力手册》[5]中将降雪情况分为小雪、中雪、大雪、暴雪等4类，并列出了分类标准及其对通行能力及速度的影响程度。但是，在不同地区冰雪天气的发生频率及影响程度不同以及驾驶员应对冰雪的经验技巧的差异会间接影响冰雪条件下交通流的运行规律。因此，为了制定切实、合理的控制策略，在实际应用中应针对控制地区的路段具体调查其受冰雪影响时的交通流特性。

本文选取长春市南部快速路卫民街与卫星路交汇处的快速路汇入区路段进行研究，调查地点如图1所示。

图1 调查地点Fig.1 Study site

该路段入口匝道上游为地下隧道，下游2000 m区域为高架桥且没有出口匝道，因此避免了城市道路上车辆行驶的干扰。此外，该路段的交通需求较大，在早、中、晚3个时间段均会产生由汇入车辆交织导致的严重交通阻塞，是长春市常发性拥堵路段之一。考虑到实际数据获取的难度，并与实际情况(长春市的快速路应急除雪工作较为及时)结合，本次研究拍摄了正常天气及除雪后快速路交通运行的视频，并采集交通流数据以交通流状态转变过程中的关键交通流参数表征冰雪的影响，如表1和表2所示。

(1)自由流速度：指道路上处于非跟驰状态下车辆的行车速度。可以通过分析不同车头时距时前、 后两车速度的相关系数得到跟驰状态的临界值，然后根据前、后车头时距大于临界值时的后车行车速度的统计值确定。

表1 城市快速路主线交通流数据Table 1 Traffic flow data of urban expressway′s main line

表2 城市快速路交织区交通流数据对比Table 2 Traffic flow data of urban expressway’s merging area

(2)跟驰状态起始密度：指交通流由自由流状态向跟驰状态转变时的密度。

由于实测时，道路上两种交通流状态发生转变的时间不能直接准确地获取，其对应的跟驰状态起始密度也不能直接获得，所以本文首先确定自由流车速和临界跟驰车头时距，然后根据式(1)计算跟驰状态起始密度[6]：

(1)

式中：Dg为跟驰状态起始密度；vf为自由流速度；t0为临界跟驰车头时距，其中，利用前后车速度相关性分析的方法确定临界跟驰车头时距[6]，将交通流从自由流向跟驰流过渡的车头时距(0～10 s)分为9个区间，然后对不同区间前、后两车的车速进行相关性分析。两种天气下交织区交通流车速相关性分析结果如表3所示。

由表3可知，正常天气条件下，当车头时距小于6 s时，前、后车速度具有相关性；当车头时距大于6 s时，前、后车速度不具有相关性，因此正常天气条件下交织区的临界跟驰车头时距为6 s。同理，可得冰雪天气下的临界跟驰车头时距为8 s。结合已测得的自由流速度值，代入式(1)中，可得两种天气下跟驰状态起始密度分别为9.68、8.33 veh/km，由于该数值为车流密度，车辆数四舍五入取整后分别为10、8 veh/km。

(3)最大通行能力和最佳密度：最大通行能力取调查时段内每20 s车道截面通过的最大流率，最大流率时段对应的密度即为最佳密度。

表3 交织区前、后车速度相关性分析Table 3 Correlation analysis of velocities before and after merging area

(4)停车波波速：交织区瓶颈形成时交通波向上游传播的速度。

在测量过程中，分别测量停车波起始位置至其传递至上游某一固定位置的距离和所用时间，两者相除得出波速，并选取多个拥堵形成的过程，多次计算后求平均值作为停车波波速的最终值。

(5)突变后流率：指道路车辆密度达到最佳密度后继续增大，通行能力突降后的流率[7]。

图2 交织区流率-密度散点图Fig.2 Scatter plot of traffic flow and velocity

通过对冰雪条件下快速路交织区每20 s的流率统计及对快速路交织区的流率-密度散点图(见图2)的绘制发现，冰雪条件下的快速路交通流同正常天气条件下一样，在由自由流向阻塞流发展的过程中会发生通行能力突变现象。在确定阻塞密度kj、停车波波速w及最佳密度km后，由几何知识可得突变后交织区流率的计算公式：

Qd=w(kj-km)

(2)

式中：Qd为突变后流率。

(6)阻塞密度：交通严重阻塞时单车道每千米路段所包含的车辆数。

由表1和表2可得：与正常天气条件下相比，除雪后瓶颈区及其上游的自由流速度、最大通行能力、最佳密度、停车波波速等均有所降低；正常条件下瓶颈上游及瓶颈区通行能力的突变幅度分别为10.5%、12.17%，除雪后瓶颈上游及瓶颈区通行能力的突变幅度分别为15.89%、19.42%，即除雪后道路通行能力突变提前且突变幅度更大；两种道路条件下道路的阻塞密度没有明显变化。

2 可变限速控制策略

当前实际应用的快速路交通流控制方法包括匝道控制和主线限速控制，前者适用于快速路已经严重拥堵或者其他不适宜接收车辆的情况，关闭入口匝道以阻止车辆的进入；后者限速值一般取自由流的85%位车速，再根据道路线型、天气条件等因素进行修改，限速值一旦确定之后并不随交通流状态而改变，其实质为静态限速方法。上述两种方法均不是根据交通流状态确定限速值的可变限速策略，其目的是在交通需求不大时保证交通运行的安全性，而对于效率的提高并无帮助。

快速路作为一个复杂的动态系统，交通流各参数及其之间的关系会随系统内、外条件发生变化，尤其是冰雪天气下，快速路的稳定运行更易受到破坏，静态的限速显然不是最优的限速方法。因此，本文对基于快速路实时交通运行状态及根据外部条件设定限速值的方法进行了研究，以期在保证安全性的同时提高快速路运行效率。

2.1 可变限速控制方法及原理

2.1.1 可变限速控制方法

通常，限制一条道路最大运输效率的区段称为瓶颈区。在城市快速路上，瓶颈区域一般存在于车道减少处、车流汇合、分离处、转弯区域、施工区域以及发生交通事故的区域等。图3为快速路入口瓶颈区即汇流瓶颈区可变限速控制的示意图。

图3 快速路入口瓶颈区可变限速控制示意图Fig.3 Schematic of VSL control for entrance bottleneck of expressway

限速区域为瓶颈上游区域，限速长度根据具体路段灵活确定，但不应少于800 m。每隔一段时间对各检测器所得的数据进行处理，当满足限速启动条件时，根据限速策略在限速区域的可变情报板上发布限速值，并在控制区的上游对前来的车辆予以限速预告；限速值根据最近的监测数据确定，每个限速值周期性更新；在无需进行限速时，关闭可变限速控制[7]。

2.1.2 可变限速控制提高通行效率的原理

国、内外学者[7-9]在对道路上瓶颈区域的交通流进行研究时，发现了一种称为“通行能力突变(Capacity drop)”的现象，即当道路通过流率达到或接近其最大通行能力时，若密度继续增大，通行能力将突然下降的现象，如图4(a)所示。当密度达到最佳密度km，流率达到道路最大通行能力qm之后，随着密度的进一步增大，流率将迅速下降至突变后流率qd。通过前文中实际路段的调查数据可知，相同区域冰雪条件下与正常天气相比，通行能力的突变幅度更大。

图4 VSL控制提高通行能力的原理Fig.4 Principle of improving capacity using VSL

可变限速控制的目的是使瓶颈区域上游在交通需求较大时保持低流量、高密度的通行状态，从而使瓶颈区的通过流率维持在其通行能力附近。为了便于说明，画出在交通需求逐渐增大时瓶颈区流率随时间的变化图，如图4(b)所示。其中，纵轴表示流率，横轴表示时间。在t1时刻道路上交通流密度达到最佳密度km，流率达到最大通行能力qm。

若不对快速路交通流进行控制，在道路上交通流密度达到km后，瓶颈区向下游输送车辆的流率将会突然降低，如图4(b)中线段AB、BC所示；若对快速路交通流进行了合适的限速控制而使快速路瓶颈区的交通流密度不能达到km，则瓶颈区流率将维持在稍低于最大通行能力qm，但高于突变后流率qd的q′，如图4(b)中线段AD所示。此时，瓶颈区向下游输送的车辆数与无控制时相比将会得到提高，提高的数量为阴影部分四边形ACDB的面积。

2.2 基于Q学习算法的VSL控制策略设计

在制定快速路控制策略时，可以把快速路的状态演变看作一个马尔科夫过程，即快速路在控制开始时刻t0的条件下，一个控制周期T结束后它的运行状态与且仅与在此周期选择的控制动作(限制速度)有关，而与快速路在之前的状态无关。此时，可以把求限制速度的问题转化为求解马尔科夫过程的问题，而强化学习中的Q学习算法作为求解该问题的一种方法，具有以下特性[10]：①可通过与环境不断地试错交互来进行学习，不要求或较少要求先验知识；②可用于模型不确定的环境中；③是一种增量式学习方法，使用与学习可以同时进行。

在对冰雪条件下具体快速路进行限速控制的初始，并不能精确地知道各种限速动作将会对快速路的运行产生何种影响(较少的先验知识)；其次，要想建立能够精确描述冰雪条件下的快速路运行机理的模型基本不可能；最后，由于交通大环境的发展，一些在快速路区域之外影响其运行的因素也在不断变化，相对于固定的可变限速控制策略，一种能够随时根据控制效果对后续的控制策略进行修改的算法更能满足需要。

综合以上考虑，本文在获取限制速度的过程中选择了Q学习算法。

2.2.1Q学习算法原理[10]

Q学习算法是强化学习算法的一种，在该算法中，智能体将整个学习过程分为若干次学习，每次学习的步骤如下：

(1)观察当前的环境状态st。

(2)执行一个可选动作at。

(3)观察下一个状态st+1。

(4)收到一个立即强化信号。

(5)按照式(3)调整Q值：

Qt(st,at)=

(3)

2.2.2 基于Q学习算法求限速值

本文提出的基于Q学习算法的可变限速控制(简称Q-VSL)求限速值的步骤如下所示。

(1)确定交织区上游、交织区及入口匝道处的所有状态，确定可选的限速值。

(2)制定各限速情况下的即时奖励r及长远奖励Q学习的确定规则。

(3)基于仿真平台实现在各种状态下加以不同限速动作的仿真。

(4)由步骤(2)(3)得到所有状态下执行不同限速动作时对应的r值及Q学习值，并对Q学习值进行迭代直至其收敛或达到迭代次数。

(5)确定动作选择策略，并结合第(4)步得到的Q学习值确定不同状态下选择各限速动作的概率。

在步骤(1)中，快速路运行状态应包括所有影响控制效果的状态因素，动作应包括所有可选的控制行为，其确定及划分是算法成功与否的关键。本文状态及动作分类如表4所示。

表4 快速路状态及控制动作划分Table 4 Classifications of expressway states and control actions

在步骤(2)(3)(4)中，借助仿真平台在各种状态组合中加入不同的控制动作，并根据其控制效果确定对应的即时奖励值，且越是有利于提高其运行效率的，即时奖励值越大(本文中即时回报值取在单一限速时间段内瓶颈区通过的车辆数)。之后，按照式(3)合理地选择系数对Q学习值进行更新。

在步骤(5)中，所得的表中包含各状态与不同动作对应时的Q学习值，结合选择策略(贪心算法)可以确定各个状态下各限速动作的选择概率。实际应用中，该Q学习值表能够根据应用效果进行不断更新。

2.2.3 可变限速控制策略设计

图5 Q-VSL控制策略流程图Fig.5 Flow chart of Q-VSL control strategy

本文提出的Q-VSL控制方法流程如图5所示。为了避免由于车辆速度波动较大引起的交通安全问题，本设计规定限速值每6 min更新一次，最新一次所取的限速值需在上次限速值及与其相邻的两个值中选取，即根据实际交通系统状态和Q学习学习结果所得的限速值与上一时间段的限速值相差不超过20 km/h。每次限速值发布之后，根据6 min之后的交通系统状态评价该次限速控制的效果，并据此对控制之前的状态对应的各可选动作的Q学习值及被择概率表进行更新，这体现了本文控制算法的持续在线学习能力，该能力能够弱化在算法中考虑不足和已经发生变化的因素对控制效果的影响。因此，该算法的应用时间越长，控制效果越好、越稳定。

3 仿真验证

基于Q学习算法求限速值时，为了避免求值过程中可能出现的状态遗漏，把交通流状态、系统输入及天气条件3类状态参数进行组合，在这些组合中显然存在大量不可能出现的状态，也不可能对那些状态进行实际的限速操作；此外，为了保证交通安全也不可能对实际出现的状态进行各种限速值控制的试验。为了解决以上问题，本文选择交通流仿真技术对提出的可变限速策略进行验证。

3.1 元胞传输模型及其改进

本文研究目的是提高快速路的通行效率，在综合考虑是否能够满足模拟关键的交通流特性、模型参数标定的难易、能否加入可变限速控制以及仿真时间的基础上，本文采用元胞传输模型，以Matlab为仿真平台对本文限速策略进行了验证。

3.1.1 基本CTM模型

元胞传输模型(Cell transmission model，CTM)是宏观动力学模型LWR模型的差分离散形式，由美国科学家Daganzo于1994年提出[11]，被用来对快速路交通流及城市路网交通进行仿真模拟。

基本的元胞传输模型将时间划分为相等的时间间隔(即仿真步长)T0，路段分为若干等距小段(称为元胞)L0来模拟实际道路上的交通流运行。其中，每个元胞的长度等于自由流速度与仿真步长的乘积，且元胞内的流量与密度符合图6所示的梯形函数关系。图中，q为交通流流率；vf为自由流速度；k为交通流密度；qmax为元胞最大通行能力；w为拥堵形成时向上游传播的交通波波速；kj为阻塞交通流密度。

图6 经典的CTM交通流基本图Fig.6 Traffic flow chart of classic CTM

在模拟道路运行时，每一时刻系统的状态由各元胞中所含的车辆数确定。元胞i在步长t时段内从上游元胞接受的车辆数情况可由式(4)得到：

Js(i,t)=

(4)

式中：Js(i,t)为元胞i在步长t时接受的车辆数；N(i)为元胞i所能包含的最大车辆数；n(i,t-1)为元胞i在步长(t-1)结束时所包含的车辆数。

3.1.2 CTM模型的改进

基本的元胞传输模型能够模拟道路上常规的交通流运行如拥堵的形成及消散，交通波的生成及传播等，但是，其对于交通流流量与密度的关系的假设过于简单，既无法体现车辆较多时道路上车辆的时走时停现象，也无法体现瓶颈区拥堵形成时的通行能力突变现象，而且在同步流时通过流量不变的假设与事实存在明显差异。为了更真实、精确地反映快速路实际运行情况，本文在实际调查数据的基础上对元胞传输模型的交通流基本图做了如下改进：

(1)自由流枝的改进

图7 CTM流率-密度基本图自由流枝的改进示意图Fig.7 Schematic of improvement of free flow branch in fundamental volume-density diagram of CTM

在经典的交通流梯形关系图的中，假设车辆可以由自由流速度行驶直至达到道路的通行能力，如图6所示。而实际中，在道路密度由零逐渐增加的过程中，初始阶段由于车流密度较小，车辆可以以自由流速度行驶，如图7(a)中线段AB所示，道路通过流率随着密度呈正比上升；随着车流密度进一步增加，车辆间距变小，车辆之间的相互干扰加重，致使车速逐渐降低，但是此时的道路通过流率仍然是增加的，只是增速有所放缓，直至到达最大通行能力，如图7(a)中曲线BC所示。为此，在本研究中对CTM中的交通流基本图的自由流部分做了如图7(b)所示的改进。

在图中，自由流枝包括两段，称为完全自由段OD与部分自由段DF，其中，kf为车两段之间衔接处的交通流密度；km为最佳密度。

(2)瓶颈区通行能力突变现象及滞后效应的改进

滞后效应[12]指的是在交通流状态转变过程中，自由流与拥堵流之间的车流密度存在重叠的部分，且从自由流向拥堵流过渡时的车流密度大于由拥堵流向自由流过渡的密度。本文通过实际采集到的数据绘制流率随密度变化的散点图(见图2)，验证了该现象。为了体现这种现象，对瓶颈区元胞的交通流基本图做如图8所示的改进[13]。

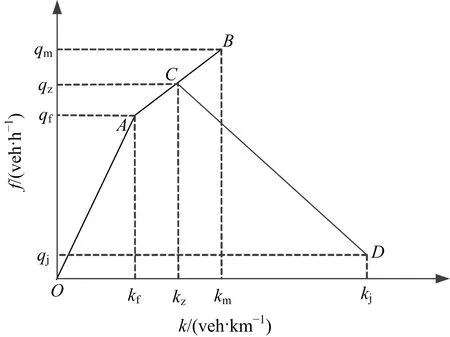
图8 CTM流率-密度基本图中加入突变和滞后效应的改进示意图Fig.8 Schematic of fundamental volume-density diagram of CTM inlaid capacity gap and hysteresis effects

图8中，kz为从拥堵流向自由流转变时的交通流密度；qz为对应的交通流密度。通过实测数据得到kf、qf、km、qm和w时，可通过计算得到kz和qz。当kzkj之后的部分，为了避免元胞路段交通流密度达到阻塞密度之后将既不会接收上游车辆也不会再向下游输送车辆的现象，将车流密度大于阻塞密度之后的流率取为一较小值qj。

(3)限速影响的改进

在快速路加入限速控制后，理论上讲，只有不限速车辆行驶速度超过限速值时才有必要限速，当限速值小于自由流车速而大于无限速情况下的最佳车速时，随着密度的增大，车辆行驶速度保持不变一段时间后将减小至最佳车速(此时密度为最佳密度)；此后，基本图与无限速情况下相同(见图9(a))。当限速值小于最佳车速时，车辆将按限速值行驶至该限速值下的最大流率，然后与无限速情况下相同[7](见图9(b))。

图9 限速影响的两种情况下CTM流率-密度基本图Fig.9 Fundamental volume-density diagram of CTM of two scenarios for limiting speed

3.2 可变限速策略的仿真设计

图10为仿真路段元胞设计图，仿真路段总长度为1400 m，其中包括一个主线输入元胞①，一个匝道输入元胞⑨，一个瓶颈元胞⑥，一个终端元胞⑩，6个主线元胞(②、③、④、⑤、⑦、⑧)，单个元胞长度为200 m；入口匝道输入车辆通过元胞⑥汇入主线，交织区长度为200 m。

图10 仿真路段元胞设计示意图Fig.10 Schematic of cellular elements design in simulation segments

在仿真程序的开始，需要对各个元胞进行初始化。初始化包括确定各元胞当前所包含的车辆数，输入元胞的输入速度随时间的变化关系，以及非输入元胞内部车辆运行所遵循的交通流基本图(见表5)。仿真时间为4 h，共1800个步长，在每个仿真步长内，各元胞中所含的车辆数将按照式(3)(4)进行更新，直至仿真结束。

表5 元胞初始化Table 5 Initialization of cellular

3.3 效果评价

为了更好地对Q-VSL控制方法进行效果评价，本文对冰雪条件(除雪后)下的快速路瓶颈汇流区域进行了不采用任何控制、采用基于限速模型的可变限速控制、采用Q-VSL控制等的仿真，并将控制效果进行了对比分析。其中，基于限速模型的可变限速控制的核心思想是通过分析车流量、大小车型、车道位置等因素对快速路运行速度的影响，基于车辆追尾时的临界条件以及车辆的跟驰特性，建立与道路附着系数、交通量等参数相关的安全限速模型，并利用不同冰雪路面附着系数对模型中的路面参数进行标定，进而提出分级限速的控制方法。本文参考冰雪条件下安全停车间距限速模型[4]，对于除雪后的城市快速路采用的限速值为50 km/h。

为了使仿真效果更接近于实际情况，仿真路段的流量输入采用随时间变化的形式，如图11所示。其中主线需求在仿真开始的60 min内由零匀速增加到1800 veh/h(主线通行能力)，维持30 min后，在36 min内匀速减少为720 veh/h，之后维持不变；入口匝道需求在仿真开始的60 min内由零匀速增加到600 veh/h，之后维持不变。

图11 仿真路段车辆输入Fig.11 Input of simulation road

图12 冰雪天气三种控制方法下瓶颈通过流率对比Fig.12 Comparison of flow rate at the bottleneck under three control methods in snow and ice weather

图12及表6为除雪条件下采用各种限速控制策略的控制效果对比，其中图12从左至右依次为除雪条件下无控制、模型控制以及Q-VSL控制时瓶颈区域流率随仿真步长的变化图。

由图可知，未采用任何控制与采用模型控制时的瓶颈通过流率随时间的变化基本相同，这是因为当限制速度大于路段运行最佳速度时，限制速度并不能起到限制流量的效果。在此两种控制手段下，瓶颈区流率在到达其最大通行能力之后迅速降低，之后维持在1050 veh/h左右，并在步长为1071时运行状态恢复畅通；采用Q-VSL控制之后，瓶颈区流率在到达其最大通行能力之前有一较大幅度的降低，随后升高并维持在1400 veh/h左右，且在整个仿真过程中瓶颈区未出现长时间拥堵的现象。

由表6中数据可知，模型控制相对于无控制在通行效率方面基本无提升，而采用Q-VSL控制后，每条车道在无控制的整个拥堵时间内多通过了376辆车。由此可见，本文控制方法与不予控制及模型控制相比，不仅提高了快速路入口回流区域的服务水平，也较大幅度地提高了其通行效率。

表6 控制结果对比Table 6 Comparison of control results

4 结束语

以提高城市快速路入口匝道瓶颈区通行效率为目的，提出了一种基于Q学习智能算法确定限速值的城市快速路可变限速控制策略，与其他控制策略相比，本文控制策略具有以下两个突出优点：

(1)实用性。本文控制策略简单明确、易于实施；没有建立模型应用时根据具体情况制定不同的限速策略，相对于模型法和加权法，本文方法精确度更高；相比于同样应用Q学习算法求限速值的研究，本文实现了系统动态输入下快速路限速值的确定，更接近于实际应用情况。

(2)鲁棒性。本文控制策略是闭环控制，在实际应用过程中随时根据控制效果对控制策略进行实时修改，并指导下次决策。该调整不仅可以使控制策略适应控制环境的变化，甚至可以逐渐消除策略制定过程中考虑不足的因素的影响，因此，理论上讲，该控制策略的应用时间越久，控制效果越稳定。

参考文献：

[1] 邢恩辉，王锐，韩平. 冰雪道路环境对驾驶人视觉感知特性的影响[J]. 中国安全科学学报，2012，22(3):86-91.

Xing En-hui，Wang Rui，Hang Ping. Influence of snowy and icy road conditions on driver visual perception characteristics[J]. China Safety Science Journal，2012，22(3):86-91.

[2] Knapp K，Smithson L. Winter storm event volume impact analysis using multiple-source archived monitoring data[J]. Journal of the Transportation Research Board，2000，1700(1):10-16.

[3] 邢恩辉，张明强，吴贵福，等. 寒地城市快速路冰雪路面交通流特性研究[J]. 佳木斯大学学报:自然科学版，2010，28(2):232-234.

Xing En-hui，Zhang Ming-qiang，Wu Gui-fu，et al. Traffic flow characteristics of urban expressway in the period of ice and snow of cold area[J]. Journal of Jiamusi University (Natural Science Edition)，2010，28(2):232-234.

[4] 李松龄，向涛涛. 冰雪条件下城市快速路限速研究[J]. 交通信息与安全，2015(5):55-61.

Li Song-ling，Xiang Tao-tao. A study of the speed limits under the ice and snow conditions for urban expressways[J]. Journal of Transport Information and Safety，2015(5):55-61.

[5] 美国交通研究委员会. 道路通行能力手册(精)[M]. 北京：人民交通出版社，2007.

[6] 杨小宝，张宁. 一种改进的跟驰状态判定方法[J]. 交通运输系统工程与信息，2006，6(2):14-17.

Yang Xiao-bao，Zhang Ning. An improved method of determining car-following state[J]. Journal of Transportation Systems Engineering and Information Technology,2006，6(2):14-17.

[7] 李志斌. 快速道路可变限速控制技术[D]. 南京：东南大学交通学院，2015.

Li Zhi-bin. Variable speed limit control technique on expressways[D]. Nanjing:College of Transportation,Southeast University,2015.

[8] Hao Y，Wang Y，Sun L J，et al. Research on spatial-temporal features of urban freeway congestion[C]∥The First International Symposium on Transportation and Development-Innovative Best Practices, Beijing, China,2008:185-191.

[9] Chung K，Rudjanakanoknad J，Cassidy M J. Relation between traffic density and capacity drop at three freeway bottlenecks[J]. Transportation Research Part B: Methodological，2007，41(1):82-95.

[10] 王雪松，朱美强，程玉虎. 强化学习原理及其应用[M]. 北京：科学出版社，2014:2-3，56.

[11] Daganzo C F. The cell transmission model:a dynamic representation of highway traffic consistent with the hydrodynamic theory[J]. Transportation Research Part B:Methodological,1994,28(4):269-287.

[12] Yperman I, Logghe S, Tampere C, et al. The link transmission model: an efficient implementation of kinematics wave theory for dynamic network loading[J]. Archives of Transport, 2008, 20(1/2):147-167.

[13] 杨泳，严余松，户佐安,等. 城市快速路改进型元胞传输模型及仿真[J]. 公路交通科技,2015，31(6):135-141.

Yang Yong，Yan Yu-song，Hu Zuo-an,et al. An improved cell transmission model for urban expressway and simulation[J]. Journal of Highway and Transportation Research and Development,2015,31(6):135-141.