变压器式可控电抗器的解耦工作模式

田铭兴, 李 进, 高 原, 柳轶彬， 闵永智

(1. 兰州交通大学自动化与电气工程学院, 甘肃 兰州 730070; 2. 兰州交通大学甘肃省轨道交通电气自动化工程实验室, 甘肃 兰州 730070; 3.西南交通大学电气工程学院, 四川 成都 610031; 4. 西安交通大学电气工程学院, 陕西 西安 710049)

无功平衡和电压稳定是电网安全可靠,经济运行的重要保证,所以,随着我国长距离、高电压输电线路的发展,对无功补偿装置的研究已经成为必然趋势[1-2].变压器式可控电抗器(controllable reactor of transformer type, CRT)是一种新型的可控电抗器[3-4].俄罗斯学者于1995年首次提出了其基本原理,大量研究表明,CRT相比于其他无功补偿装置[5-7]具有谐波含量小、响应速度快,且能实现大容量连续可调的优点.

CRT相当于多绕组变压器[8-9],其副边(控制绕组)通过晶闸管的控制使之工作于满足一定规律的短路或开路状态.采用类似多绕组变压器同心式铁心结构的CRT,由于各控制绕组之间存在很强的电磁耦合[10],使得已经投入运行的控制绕组电流会随着其他控制绕组电流的改变而发生变化,导致各控制绕组电流在大多数工况下都低于其额定值.文献[11-12]中的磁集成CRT虽然消除了控制绕组之间的电磁耦合,实现了各控制绕组电流互不影响,但其结构复杂.若通过在各个控制绕中增加控制器的方式来解耦,势必会大大增加CRT的运行成本.所以,如何以简单经济的方式消除同心式CRT中由于电磁耦合而产生的绕组电流之间的相互影响,具有重要的研究价值.

文献[13]采用分段线性化方法,提出了各绕组瞬时电流表达式,并推导出了CRT各绕组基波电流有效值和各触发角之间的定量关系;文献[14]提出了CRT多绕组工作模式的概念,并得出了工作绕组的基波及各奇次谐波电流有效值的计算公式,并在此基础上实现了谐波优化.文献[13]和[14]的重要意义在于对CRT绕组电流有效值和触发角之间的关系进行了初步研究,并指出了可以通过晶闸管触发角的选择以达成某个控制目标.因此,如果以各个控制绕组电流互不影响为目标,就应该存在满足这一目标的触发角变化规律;反过来,如果以这样的触发角变化规律来控制各控制绕组在各周期中的开路或短路状态,就可以实现各控制绕组电流之间的互不影响,即实现了CRT的解耦控制,本文称之为解耦工作模式.

对于文献[13]中给出的CRT各绕组基波电流有效值矩阵表达式,存在以下问题:(1) 在不同计算周期内,由于各绕组的触发次序可能会发生变化,因此,最终所得的绕组基波电流矩阵中各电流不能和绕组逐一对应,使其不便于应用;(2) 未对各绕组各次谐波电流的计算进行分析.文献[14]只给出了工作绕组电流的电流计算模型,并未对各控制绕组电流进行分析,也不够全面.所以,本文首先针对文献[13-14]中的不足,改进CRT绕组电流计算模型使之更加便于应用;其次,在给出解耦工作模式原理并分析其特点的基础上,研究满足各绕组额定电流的限流电感和使各绕组电流互不影响的触发角的计算方法.最后,通过一个算例来说明上述工作的正确性.

1 绕组电流计算模型

CRT的工作原理如图1所示.

图1 CRT工作原理Fig.1 Schematic diagram of CRT

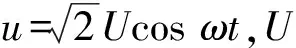
各物理量说明如下:

定义绕组电流矩阵为

I=[I1I2…Ik…In]T,Ik为绕组Wk的电流有效值;

绕组自互感矩阵为

对角线元素为各绕组自感,非对角元素为各绕组间的互感;

限流电感矩阵为

L=diag[0LX2…LXk…LXn],LXk为绕组Wk中串联的限流电抗器的电感;

触发角矩阵为

α=[α1α2…αk…αnπ/2],αk为绕组Wk中串联的反并联晶闸管触发角(假设工作绕组中也串联了一组反并联晶闸管,α1≡0°);

将α中的元素按从小到大的顺序排列(大小相等时,绕组编号小的在前)可得新的触发角矩阵,记为

β=[β1β2…βi…βnπ/2],

(1)

对于式(1)显然有

β1≤β2≤…βi≤…βn;

(2)

由α和β可构成一个n阶方阵P,其元素为

(3)

上述各式中:1≤i≤n, 1≤j≤n.

则得电感矩阵Ln如式(4)所示.

Ln=P(M+L)PT.

(4)

文献[13]求出了各绕组在周期内各个时段上的瞬时电流表达式,并对其进行傅里叶分解得出了各绕组的基波电流有效值表达式,基于以上工作,若对其进一步傅里叶分解,并考虑各周期内的触发次序的不同,可得各绕组的各次谐波电流有效值如式(5)所示.

(5)

式中:

Ik(2m-1)=[I1(2m-1)I2(2m-1)…Ik(2m-1)…In(2m-1)]T,Ik(2m-1)表示绕组Wk的2m-1次谐波电流有效值,m=2,3,…;

U1为工作电压的有效值；

h[·]为对该矩阵中的各元素取其绝对值后的矩阵;

V=(O,E)-(E,O),E为n阶单位方阵,O为n×1阶零向量;

fm(β)=[fm(β1)fm(β2) …fm(βn)fm(π/2)]T,

其中:

fm(x)=

Y是一个上n×n阶的三角矩阵,由图2所示步骤得来.

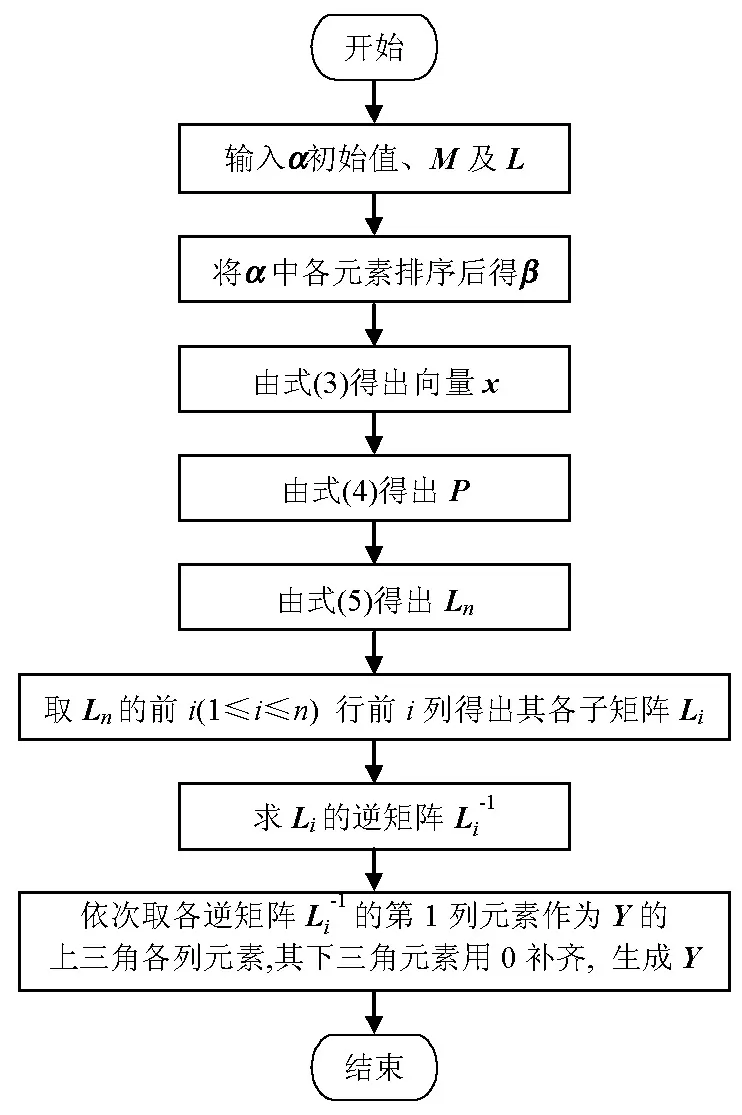
图2 Y的计算流程Fig.2 Calculation flowchart of Y

若只考虑2M-1次及以下的奇次谐波,各绕组电流有效值为

I=[I1I2…In]=

(6)

可将式(6)简记为

I=f(M,L,α).

(7)

式(7)即为CRT的绕组电流矩阵I和绕组自互感矩阵M、限流电感矩阵L,以及触发角矩α之间关系的具体表达式.

对于已经制成的CRT来说,式(8)中的M是已知的,因此,当给定I、L、α中的任意两个量时,就可由式(8)求解出另外一个量.

2 CRT解耦工作模式原理

CRT现有的工作模式中,顺次单支路工作模式具有谐波电流小,调节简单的优点,因此本文选用顺次单支路工作模式和解耦工作模式进行比较分析.

由于CRT各绕组之间存在电磁耦合,且在顺次单支路工作模式下,始终只有一个控制绕组处于调节状态[17],所以已经达到短路状态的控制绕组电流会随着后续绕组的调节发生变化,文献[18]算例中的6绕组CRT为例,在顺次单支路工作模式下,各控制绕组电流变化趋势如图3所示.

图3 顺次单支路工作模式下各控制绕组电流与工作绕组电流的关系Fig.3 Relationship between the working winding current and control winding current under sequential single branch operation mode

所谓CRT的解耦工作模式,就是当以某种特殊的触发角变化规律来调节各晶闸管时,各控制绕组电流达到其额定值(即其最大值)后都保持恒定不变,不受其它控制绕组的工作状态变化的影响.以6绕组的CRT为例,采用解耦工作模式后,各控制绕组电流与工作绕组电流关系应如图4所示.

图4 解耦工作模式下各控制绕组电流与工作绕组电流的关系Fig.4 Relationship between the working winding current and control winding current under the decoupling operation mode

图4中,纵坐标I2N、I3N、…、I6N分别为解耦工作模式下各控制绕组的额定电流;此时,所有控制绕组电流都达到其额定值(所有晶闸管都全导通),因此,I1(5)就是工作绕组的额定电流.

图4所示解耦工作模式具有以下特点:(1) 控制绕组依次投入运行;(2) 当前一个控制绕组电流达到其额定值时,后一个控制绕组才开始投入运行;(3) 各控制绕组电流在达到其额定值之后,一直保持在该额定值不变,不受后续控制绕组的电流变化影响;(4) 工作绕组电流达到其额定值时各控制绕组的电流均为其额定值.

3 触发角计算

当已知M、L,并给定各控制绕组电流I2、I3、…、In后,可由式(8)求得控制绕组所串联的晶闸管触发角α2、α3、…、αn,以及工作绕组电流I1.

根据图4所示CRT解耦工作模式的特点,各控制绕组电流给定方法如下.

首先需要已知各控制绕组的额定电流I2N、I3N、…、InN.之后,可将整个调节范围分为n-1级,在各级内只有一个控制绕组电流从0增大到其额定值,且其余控制绕组电流保持不变(或额定值或0).例如,在第k-1(2≤k≤n)级中各控制绕组电流情况如下:

当k=2时:Ik=I2∈[0,I2N],I3=I4=…=In=0;

当3≤k≤n-1时:I2=I2N,I3=I4,…,Ik-1=I(k-1)N,

Ik∈[0,IkN],Ik+1=…=In=0;

当k=n时:I2=I2N,I3=I4N,…,In-1=I(n-1)N,

Ik=In∈[0,InN].

这样,若将上述各级内[0,IkN]按一定的步长进行离散,对应每一个离散点,可给定各控制绕组电流.

按上述分段离散法,只要离散步长足够小,所求得的相应离散点的触发角α2、α3、…、αn,和工作绕组电流I1就有足够的精度.若按由此得到的触发角随工作绕组电流的变化规律来控制各晶闸管,就可实现图4所示的解耦控制.

4 限流电感计算

由第3节分析可知,当各控制绕组的电流确定后,若要求解实现解耦的触发角,还需确定M、L.对于结构确定的CRT,M可由文献[18]所述方法得到,而L可通过下述方法求得.

根据解耦工作模式的特点,最后一个控制绕组电流达到其额定值,所有晶闸管的触发角都为0,此时,各控制绕组电流均为其额定值.

由图1可知,若忽略绕组电阻和铁心磁饱和非线性,当所有晶闸管的触发角都为0(所有晶闸管全导通)时,可按照正弦稳态电路求解L,因此:

U1-ωLI1=ωMI1,

(8)

式中:I1=[I1I2…Ik…In]T;

U1=[U10 … 0]T.

由式(8)得:

(9)

式中:

I2=diag[0I2I3…In];

L1=[I1LX2LX3…LXn]T.

由式(9)可得:

(10)

式中:

I3=[I2I3…In]T;

由式(10)可得:

(11)

所以,当已知M、工作电压额定值U1N和各控制绕组的额定电流时,通过求解式(11)所示的方程组,即可得出工作绕组的实际额定电流I1N及各限流电感大小,且此处求出的工作绕组额定电流I1N中包含了励磁电流.

5 算例分析

[I2NI3NI4NI5NI6N]=

[9.16 11.59 24.52 51.85

109.64] A,

自互电感矩阵(单位为H)为

将上述条件代入式(11),可得

L1=[208 A 40.223 H 30.184 H

12.830 H 5.376 H 2.121 H].

L1中,第1个元素即为CRT(工作绕组)的额定电流,其它元素为限流电感.根据L的定义,可得:

L=[0 40.223 30.184 12.830

5.376 2.121] H

由解耦工作模式的原理,可将整个调节范围分为以下5级,在各级调节范围内,各控制绕组的电流情况如下:

第1级:I2∈[0,9.16] A,

I3=I4=I5=I6=0;

第2级:I2=9.16 A,

I3∈[0,11.59] A,

I4=I5=I6=0;

第3级:I2=9.16 A,

I3=11.59 A,

I4∈[0,24.52] A,

I5=I6=0;

第4级:I2=9.16 A,

I3=11.59 A,

I4=24.52 A,

I5∈[0,51.85] A,

I6=0;

第5级:I2=9.16 A,

I3=11.59 A,

I4=24.52 A,

I5=51.85 A,

I6∈[0,109.64] A.

将各级内处于变化状态的控制绕组电流的调节范围以0.1 A为步长进行离散,即实现了对整个调节过程的离散.对于任意离散点,再根据式(7)即可得该离散点所对应的触发角向量以及工作绕组电流.

按上述方法,从第1个离散点I2=0开始逐级逐点求解,可得出整个调节范围中各离散对应的各控制绕组触发角以及工作绕组电流.由所求解出的触发角和工作绕组电流可绘出各控制绕组的触发角随工作绕组电流的变化曲线如图5所示.反过来,由所求得的触发角代入式(7)可得到各绕组电流,并绘出各控制绕组电流随工作绕组电流的变化曲线如图6所示.

可以看出的是图6和图4是一致的.同时,作为比较,图5、图6中也分别给出了顺次单支路工作模式下的各控制绕组触发角及其相应的绕组电流如虚线所示.

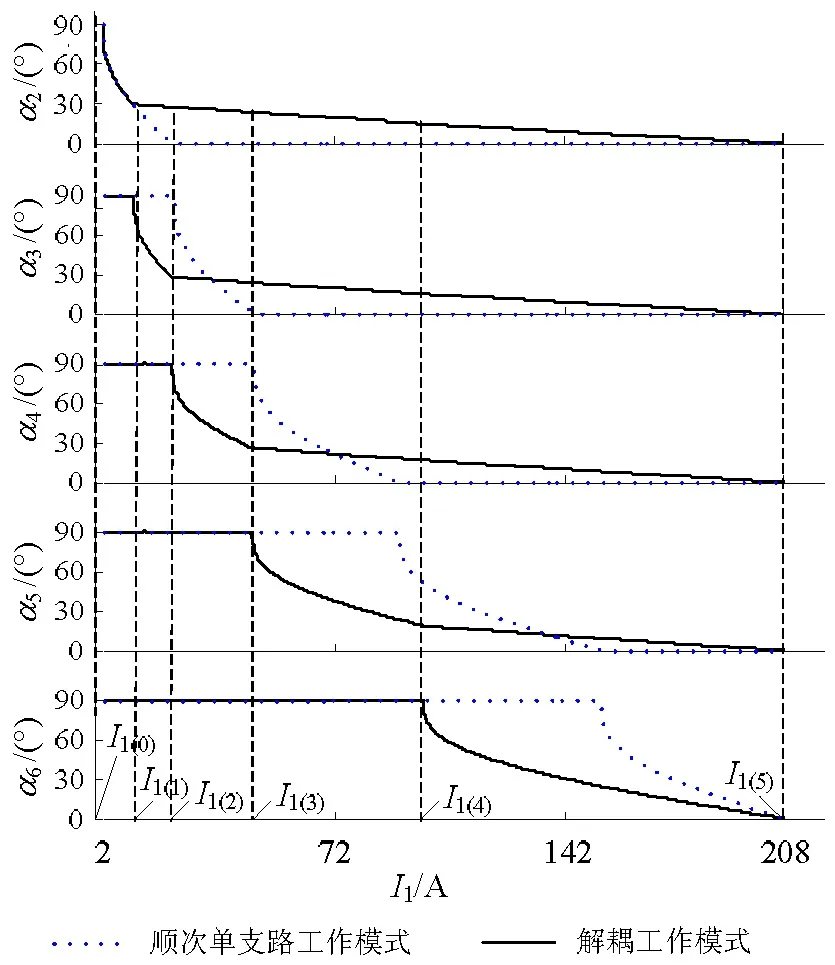
图5 各控制绕组的触发角随工作绕组电流的变化曲线Fig.5 Curve for the variation of the trigger angle of control winding with the current of the working winding

图6 各控制绕组电流随工作绕组电流的变化曲线Fig.6 Curve for the variation of the current of control winding with current of working winding

由图6可以看出,CRT满足相同的输出电流时,各控制绕组(最后一个除外)在顺次单支路工作模式下的额定电流远大于解耦工作模式下的额定电流.解耦工作模式下的控制绕组电流不受其它绕组工作状态的影响,图6所示6个关键离散点处,各控制绕组电流如表1所示.

为了更清楚说明计算结果,也作为一个例子,表2给出了图5所示6个关键离散点的计算结果.

表1关键离散点处各控制绕组电流和工作绕组电流
Tab.1 Control winding current and the working winding current at key points A

电流离散点I1(0)I1(1)I1(2)I1(3)I1(4)I1(5)I209.169.169.169.169.16I30011.5911.5911.5911.59I400024.5224.5224.52I5000051.8551.85I600000109.64I12.0311.0622.6247.0698.73207.96

表2关键离散点处触发角和工作绕组电流
Tab.2 Trigger angles and the working winding current at key points (°)

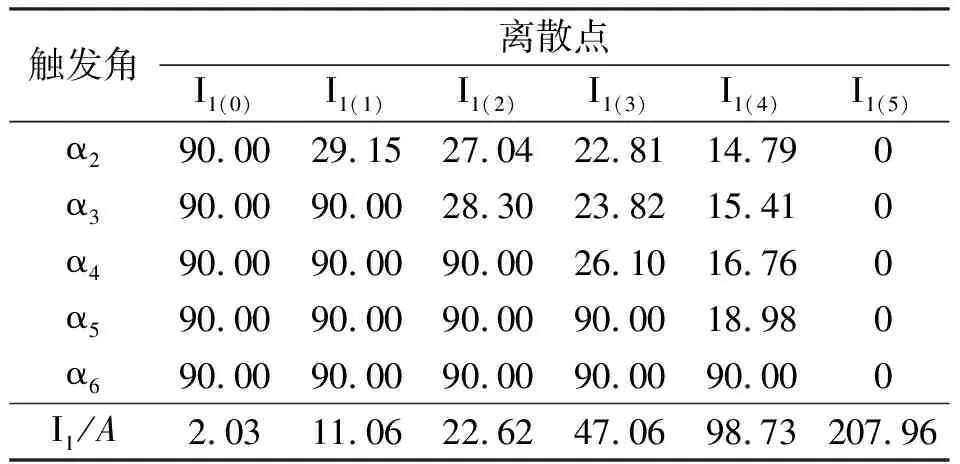
触发角离散点I1(0)I1(1)I1(2)I1(3)I1(4)I1(5)α290.0029.1527.0422.8114.790α390.0090.0028.3023.8215.410α490.0090.0090.0026.1016.760α590.0090.0090.0090.0018.980α690.0090.0090.0090.0090.000I1/A2.0311.0622.6247.0698.73207.96

从图5可以看出,CRT的工作绕组电流在[2.03,207.96] A的调节过程中,各控制绕组触发角在解耦工作模式下的调节规律.从图6可以看出在解耦工作模式下,CRT各绕组电流有效值的确能像图4所示规律变化,实现了解耦;该结果同样证明了本文第3部分所提出的限流电感计算方法的正确性.

6 结 论

(1) 改进的CRT绕组电流计算模型可对各绕组电流有效值和谐波进行计算,且便于使用.

(2) 基于多绕组工作模式的基本思想提出的CRT的解耦工作模式能够实现各控制绕组电流达到额定值后保持不变,使绕组材料的通流能力得到了充分利用.

(3) 根据解耦工作模式的特点给出的限流电感和触发角的计算方法便于编程实现.

(4) 相比于顺次单支路工作模式,输出电流一定时,在解耦工作模式下CRT各控制绕组的额定电流大大减小,这为开发性价比更高的CRT奠定了基础.

致谢：本文的研究工作得到兰州交通大学优秀科研团队项目(201701)的资助.

参考文献:

[1] 孙玉娇,周勤勇,申洪. 未来中国输电网发展模式的分析与展望[J]. 电网技术,2013,37(7): 1929-1935.

SUN Yujiao, ZHOU Qinyong, SHEN Hong. Analysis and prospect on development patterns of China’s power transmission network in future[J]. Power System Technology, 2013, 37(7): 1929-1935.

[2] 秦晓辉,郭强,周勤勇,等. 一种无功平衡与临界潮流快速分析方法及其在特高压可控高抗需求分析中的应用[J]. 中国电机工程学报,2013,33(19): 102-111.

QIN Xiaohui, GUO Qiang, ZHOU Qinyong, et al. Fast analysis method of reactive power balancing and critical power flow andapplication to study controllable shunt reactors requirement in UHV grid[J]. Proceedings of the CSEE, 2013, 33(19): 102-111.

[3] 周沛洪,何慧雯,戴敏,等.可控电抗器在1000 kV交流紧凑型输电线路中的应用[J]. 高电压技术,2011,37(8): 1832-1842.

ZHOU Peihong, HE Huiwen, DAI Min, et al. Application of controllable reactors to 1000 kV AC compact transmission line[J]. High Voltage Engineering, 2011, 37(8): 1832-1842.

[4] 张丽,徐玉琴. 并联电抗器在超(特)高压电网中应用及发展[J]. 电力自动化设备,2007,27(4): 75-78.

ZHANG Li, XU Yuqin. Application and development of shunt reactors in EHV & UHV transmission lines[J]. Electric Power Automation Equipment, 2007, 27(4): 75-78.

[5] 陈绪轩,田翠华,陈伯超,等. 多级饱和磁阀式可控电抗器谐波分析数学模型[J]. 电工技术学报,2011,26(3): 57-64.

CHEN Xuxuan, TIAN Cuihua, CHEN Bochao, et al. Mathematical model for harmonics analysis of the multi-stage saturable magnetic-valve controllable reactor[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 57-64.

[6] 孙媛媛,尹志明,郑伟杰,等. 晶闸管可控电抗器的谐波产生特性研究[J]. 电工技术学报,2012,27(7): 267-273.

SUN Yuanyuan, YIN Zhiming, ZHENG Weijie, et al. Study of the harmonic producing characteristics of the thyristor controlled reactors[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 267-273.

[7] 张宇,陈乔夫,李江红,等. 一种用于电气化铁道无功补偿的可控电抗器[J]. 电工技术学报,2011,26(8): 166-171.

ZHANG Yu, CHEN Qiaofu, LI Jianghong, et al. A controllable reactor for reactive power compensation of electrified railways[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 166-171.

[8] 刘海涛,张卫星,刘瑜,等. 变压器式可控电抗器的控制绕组无功容量分析[J]. 电力系统及其自动化学报,2006,18(6): 70-72.

LIU Haitao, ZHANG Weixing, LIU Yu, et al. Reactive power capacitance analysis for controllable shunting reactors of transformer type[J]. Proceedings of the CSU-EPSA, 2006, 18(6): 70-72.

[9] 张宇. 新型变压器式可控电抗器技术研究[D]. 武汉:华中科技大学,2009.

[10] 田铭兴,原东昇,安潇,等. 变压器式可控电抗器绕组电流分析[J]. 高电压技术,2014,40(1): 269-274.

TIAN Mingxing, YUAN Dongsheng, AN Xiao, et al. Analysis on winding current of controllable reactor of transformer type[J]. High Voltage Engineering, 2014, 40(1): 269-274.

[11] 田铭兴,尹建宁,柳轶彬,等. 基于磁集成技术的变压器式可控电抗器的结构设计与分析[J]. 高电压技术,2014,40(10): 3141-3149.

TIAN Mingxing, YIN Jianning, LIU Yibin, et al. Structure design and analysis of controllable reactor of transformer type based on magnetic integration technology[J]. High Voltage Engineering, 2014, 40(10): 3141-3149.

[12] 田铭兴,付鹏宇,黎宁昊. 磁集成变压器式可控电抗器结构及其磁路与电路分析[J]. 西南交通大学学报,2017,52(4): 774-781.

TIAN Mingxing, FU Pengyu, LI Ninghao. Magnetically integrated structure for transformer-type controllable reactors: magnetic circuit and circuit analysis[J]. Journal of Southwest Jiaotong University, 2017, 52(4): 774-781.

[13] 田铭兴,柳轶彬,尹健宁,等. 变压器式可控电抗器绕组电流与触发角的关系[J]. 电力自动化设备:2014,34(8): 122-127.

TIAN Mingxing, LIU Yibin, YIN Jianning, et al. Relationship between CRT winding current and firing angle[J]. Electric Power Automation Equipment, 2014, 34(8): 122-127.

[14] 田铭兴,柳轶彬,郭毅娜,等. 基于多绕组调节模式的变压器式可控电抗器谐波电流优化[J]. 电网技术,2015,39(10): 93-99.

TIAN Mingxing, LIU Yibin, GUO Yina, et al. Harmonic current optimization of controllable reactor of transformer type based on multi-winding regulation mode[J]. Power System Technology, 2015, 39(10): 93-99.

[15] TIAN Mingxing, LI Qingfu, LI Qunfeng. A controllable reactor of transformer type[J]. IEEE Transactions on PowerDelivery, 2004, 19(4): 1718-1726.

[16] TIAN Mingxing. Analysis of transformers on the concept of elementary winding[J]. Electrical Engineering, 2007, 25(9): 553-561.

[17] 柳轶彬,田铭兴,尹建宁. 变压器式可控电抗器的单绕组调节模式及谐波电流优化[J]. 电力自动化设备,2015,35(7): 74-82.

LIU Yibin, TIAN Mingxing, YIN Jianning. Single-winding regulating mode and harmonic current optimization of controllable reactor of transformer type[J]. Electric Power Automation Equipment, 2015, 35(7): 74-82.

[18] 田铭兴. 变压器式可控电抗器的基本理论研究[D]. 西安:西安交通大学,2005.