高雷诺数下方柱绕流特性的数值模拟
周 强, 廖海黎, 曹曙阳
(1. 西南交通大学风工程四川省重点实验室, 四川 成都 610031; 2. 同济大学土木工程防灾国家重点实验室, 上海 200092)
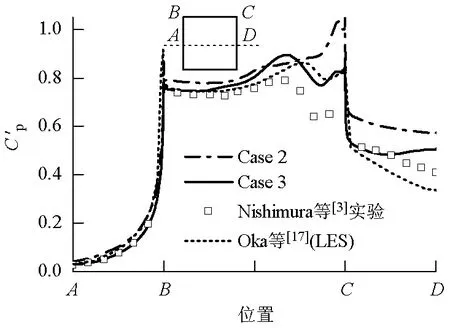
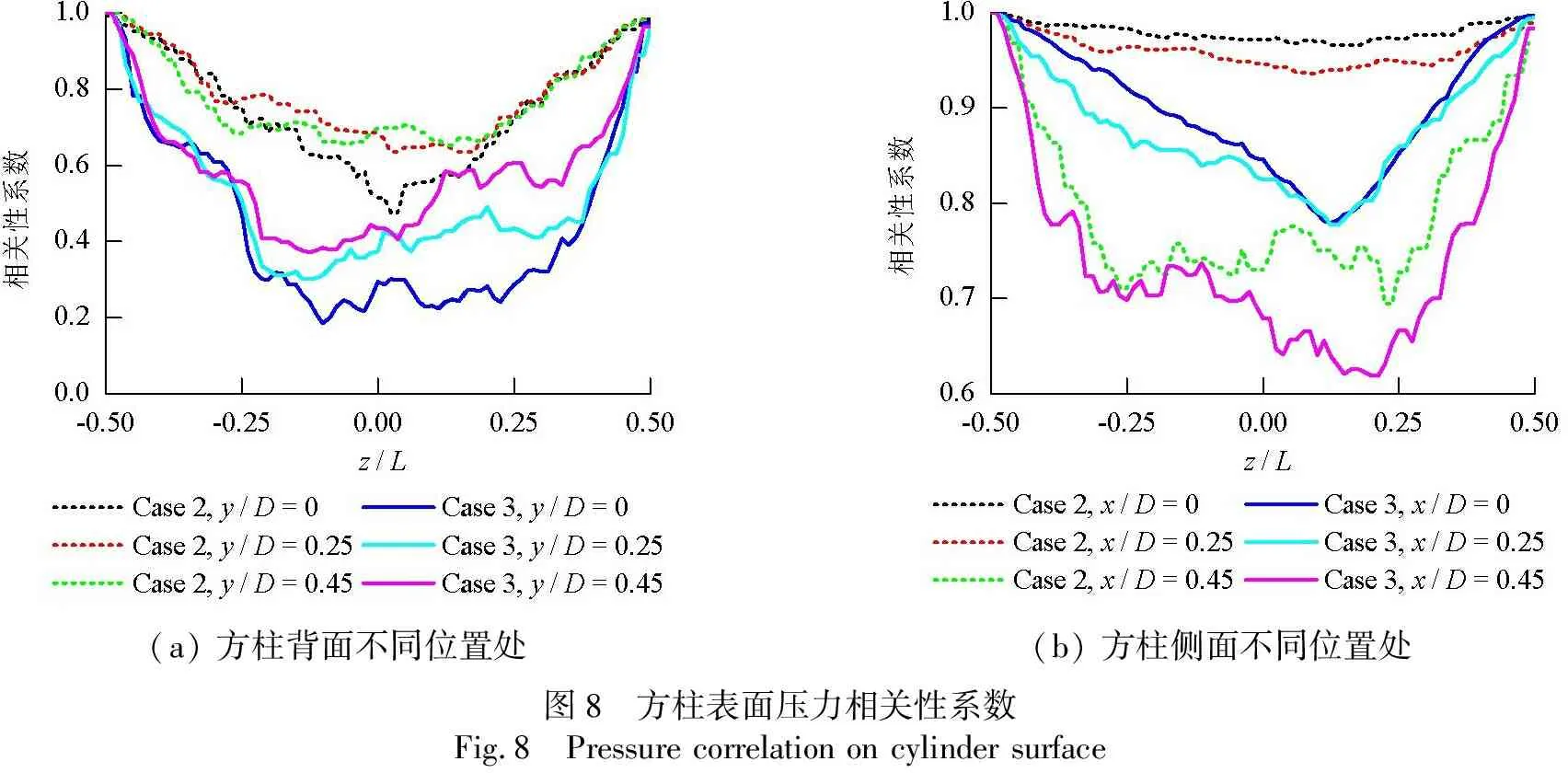
长期以来,方柱绕流一直是风工程、钝体空气动力学、海洋工程等研究领域重要的、基础性的热点问题.在实际工程应用中,如桥梁的桥塔和桥墩、高层建筑、海洋平台等具有方柱形状的构件,在风或者水流作用下,会产生有规律的大尺度旋涡脱落现象,致使结构发生风致振动,进而导致其受损或发生疲劳破坏.因此,研究在方柱绕流问题及其尾流结构对于实际工程设计和建造具有十分重要的意义.
不同雷诺数下,流体绕过方柱呈现出明显不同的流动特性.其中在高雷诺数下,流体经方柱前端边角后发生明显的流动分离,并伴随着回流或转捩,形成大尺度和不稳定的旋涡脱落,即与低雷诺数下流场相比,高雷诺数下的方柱绕流特性更加复杂,且表现出更加显著的三维特性.鉴于此,若采用雷诺时均方法,很难扑捉到准确的高雷诺数下方柱绕流特性;由于计算量太大,目前直接数值模拟还只限于雷诺数较低的流动.因此,对于高雷诺数方柱绕流问题,主要的数值研究方法就是大涡模拟(large eddy simulation, LES)方法.
到目前为止,国内外学者针对方柱绕流问题开展了大量而丰富的实验和数值模拟研究.在实验研究方面,Lyn等[1]通过水洞实验,采用LDV(laser doppler velocimetry)技术研究了Re=21 400下的方柱绕流特性,详细分析了其尾流结构,同时其研究结果也广泛被作为数值模拟的参考标准;此后国外学者Saha等[2]在风洞中对高雷诺数下方柱的绕流特性进行了深入研究;近年来,Nishimura和Taniike[3]通过试验详细研究了不同攻角下方柱绕流特性;Yen等[4]利用粒子图像测速技术(particle image velocimetry, PIV)研究了方柱在4 000 综上可见,对于高雷诺数下方柱绕流的数值模拟,因其流动的复杂性和明显的三维特性,此时,采用LES是比较合适的选择.然而如上文所述,大多采用LES方法模拟中展向长度的选取等细节问题还是存在不够明确的地方,导致一些流场速度、气动力等关键参数的脉动项与实验结果存在一定差别.为此,本文基于开源CFD软件OpenFoam平台,采用基于动态亚格子模型的大涡模拟方法,在Re=22 000情况下,对均匀来流条件下的不同网格系统、展向长度的方柱绕流问题进行了三维数值模拟,首先对数值结果的准确性进行验证,然后重点分析断面周围网格以及长径比对尾流区流场结构的影响,并给出不同长径比下气动力的展向空间相关性. 经过滤波后,大涡模拟的连续性和N-S方程为 (1) (2) (3) 式中:τkk为应力,k=1,2,3;δij为 Kroneker符号;Sij为变形速率张量;vSGS为亚格子模型涡粘系数, (4) (5) 其中:Lkk为亚格子Leonard 应力;Lij和Mij的表达式分别为 其中,Δ为格子过滤尺寸标准. (1) 计算区域 本文共计算3个算例,其中Case 1和Case 2的计算区域为30D×18D×4D(D为方柱断面宽度),Case 3则为30D×18D×8D.方柱模型上游来流区域长度为10D,下游尾流区长度为20D,即x方向上的长度为30D;模型离上下边界各为9D,即y方向上的宽度为18D;为了研究长径比的影响,展向长度分别取4D和8D两种长度,如图1所示. 图1 计算区域示意图及边界条件Fig.1 Computational domain and boundary conditions (2) 边界条件(如图1所示) 方柱表面边界条件:采用无滑移光滑固壁边界; 入口边界条件:采用均匀来流速度条件,U=10 m/s;拟压(pseudo-pressure)φ采用Neumann条件; 出口边界条件:速度满足格式为 ∂/∂t+c∂/∂x=0 的对流边界条件,拟压取为0,这里c为任意常数; 上下边界条件:采用自由流动边界条件; 展向边界条件:采用周期边界条件. (3) 网格划分 (4) 数值算法 在空间离散上,本文采用NVD(normalized variable diagram)格式,从而避免中心差分引起的非物理性振荡.对于时间的离散格式,采用二阶完全隐式法,以获得稳定并准确的结果.为避免计算中的数值振荡问题,本文在数值算法上采用了MIM(momentum interpolation method)方法[14];对N-S方程组采用Piso求解算法,并将连续性方程的收敛值设置为1×10-6;无量纲时间步长设置为Δt*=ΔtU/D=2.5×10-4,以确保柯朗数小于1,且保证每步计算可在20次迭代内完成. 图2 整个计算区域内网格划分情况Fig.2 Grid system (a) Case 1(b) Case 2和Case 3图3 方柱表面周围网格划分情况Fig.3 Grid around square cylinder 本节针对基于时间积分的平均积分分量,与其他实验和数值结果进行了比较,以确保本文数值计算的准确性. 如表1所示,本文3个算例得到的St均与Lyn等[1]和Norberg[15]的实验值比较吻合;平均阻力系数CD与Sohankar等[5]的LES结果间误差小于1%,两者结果十分接近. 需要指出的是,表1中计算气动力系数所采用的特征长度均为方柱断面宽度D.由此可见,本文进行的数值模拟是准确和可靠的. 表1 平均积分分量对比表Tab.1 Comparison of integral parameters 同时由表1可以发现,与Case 1中各项气动力参数的结果相比,Case 2和Case 3结果更加准确,即在方柱表面附近先布置厚度均匀的正交网格,可有效改善数值结果.因此以下将主要针对后两者的结果进行说明. (a) 平均值 (b) 脉动值图4 方柱表面压力分布Fig.4 Surface pressure distribution on square cylinder 由图4可见,本文结果与其他实验和数值结果基本吻合;且与Oka等[17]的数值结果相比,本文更加接近Nishmura等[3]的实验值.如图4(b)所示,与Case 2相比,Case 3中的脉动值与实验值更加吻合,特别是在方柱背面区域和靠近后方边角附近区域,也就是旋涡主要作用区域.这再次表明气动力系数的脉动值对展向长度更敏感. 图5给出并比较了中心平面(y=0的平面)上平均流向速度的分布情况. 图5 中心线上的平均流向速度分布Fig.5 Stream-wise velocity at centreline 在尾流区,本文的结果较Wang等[8]的结果更加与实验值一致.但可以发现各个结果间的Lr偏差较小,而Umin/U比值偏差更大.其原因在于Umin/U较Lr对长径比更加敏感,因此,Case 2和Case 3的Umin/U比值也因为展向长度的不同而出现不同的结果.与此类似,Norberg[18]在研究圆柱绕流时,对比不同的长径比和阻塞率的试验结果后,也发现Umin对长径比更加敏感. 流动速度的脉动值和雷诺应力分布都是流场结构中重要的湍流特征,因此可通过对速度脉动值和雷诺应力的分析,研究方柱尾流结构中的湍流特性. (a) 平均流向速度(b) 平均竖向速度图6 尾流区不同位置处平均速度分布Fig.6 Mean velocity profile in the wake 由于旋涡的交替出现使得尾流区流向速度脉动值的峰值不在中心处,而是在两侧出现双峰值,如图7(a)所示.这说明在尾流区存在明显卡门涡街现象.然而随着流动向下游发展,峰值对应的尖角消失,变得更圆滑,甚至消失.这说明旋涡在下游发展中逐渐减弱.如图7(b)所示,尾流区不同位置处的脉动竖向速度均在在中心线上达到峰值,即存在单个峰值.因此表明交替出现的旋涡对流向和竖向上速度脉动值的影响是不同的.如图7(c)所示,由于交替旋涡的出现,雷诺应力(u′v′)呈现关于y=0轴的反对称性.此外以上三者均在位置x/D=1.5处达到峰值,然后随着流向而逐渐衰减,这表明旋涡强度最大值对应的位置在x/D=1.5附近,即回转长度大约为1.5D,再次证明了表1中得到的回转长度是合理准确的. 同时可以发现,本文Case 2和Case 3结果均与其他结果基本吻合,但Case 3的结果更加接近Lyn等[1]实验值.由此可见,速度的脉动值对展向长度,即长径比更加敏感,因此为保证得到准确的湍流流场特性,需要选择合理长径比. 为了进一步研究展向长度(长径比)对流场的影响,本文在方柱表面不同位置上,沿展向布置了一系列监测点,并通过分析得到其压力的相关性系数,如图8所示. 由于展向采用周期边界条件,因此压力的相关性系数在两侧均等于1.同时可以发现随着长径比的增加,背面和侧面的压力相关性均减弱.背面压力相关性的减弱导致方柱的阻力系数的平均值和脉动值均有所减小,如表1所示;而侧面压力的减弱使得升力的脉动值明显减小,从而使得其值与实验结果更加吻合.因此,在对方柱绕流进行数值模拟时,为保证获取准确合理的平均和脉动气动力,以及准确的流场湍流特性,取8D的展向长度是十分必要的. (a) 脉动流向速度(b) 脉动竖向速度(c) 雷诺应力(u′v′)图7 尾流区不同位置处的脉动速度分布Fig.7 Fluctuating wake velocity (a) 方柱背面不同位置处(b) 方柱侧面不同位置处图8 方柱表面压力相关性系数Fig.8 Pressure correlation on cylinder surface 在典型高雷诺数Re=22 000下,本文基于开源软件Openfoam平台,采用大涡模拟方法,对不同网格划分体系、不同展向长度下的方柱绕流进行三维数值模拟研究,在验证了数值结果的准确性基础上,深入分析了其尾流的流场结构和气动力特性,并给出了展向长度(长径比)对流场的影响,得到以下结论: (1) 在方柱表面附近先布置厚度均匀的正交网格,可获得更加准确的气动力结果. (2) 在方柱绕流中,回转长度是尾流结构的重要参考指标,其值大小直接影响着方柱气动力的表现,特别是断面的阻力系数. (3) 高雷诺数下,展向长度对回转长度影响较小,但对尾流流向速度分布中的Umin/U比值影响较大,即Umin/U比值对长径比更为敏感. (4) 长径比的大小直接影响方柱气动力的表现,特别是展向相关性,这使得气动力的脉动值对长径比也更加敏感,故为保证计算结果的准确性,特别为了获取更准确的湍流特性,展向长度取为8D是更为合理和有效. [1] LYN D, EINAV S, RODI W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319. [2] SAHA A, MURALIDHAR K, BISWAS G. Experimental study of flow past a square cylinder at high Reynolds numbers[J]. Experiments in Fluids, 2000, 29(6): 553-563. [3] NISHIMURA A, TANIIKE Y. Fluctuating wind forces of a stationary two dim. square prism[C]∥Proceedings of 16th National Symposium on Wind Engineering. Tokyo: Springer, 2000: 255-260. [4] YEN S C, YANG C W. Flow patterns and vortex shedding behavior behind a square cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(8): 868-878. [5] SOHANKAR A, NORBERG C, DAVIDSON L. Numerical simulation of flow past a square cylinder[C]∥The 3rd ASME/JSME Joint Fluids Engineering Conference. San Francisco: American Society of Mechanical Engineers, 1999: 18-23. [6] OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379-398. [7] SRINIVAS Y, BISWAS G, PARIHAR A, et al. Large-eddy simulation of high Reynolds number turbulent flow past a square cylinder[J]. Journal of Engineering Mechanics, 2006, 132(3): 327-335. [8] WANG G, VANKA S. Large-eddy simulations of high Reynolds number turbulent flow over a square cylinder[J]. Dept. of Mechanical and Industrial Engineering Rep. No. CFD, 1996: 96-02. [9] RODI W, FERZIGER J, BREUER M, et al. Status of large eddy simulation: results of a workshop[J]. Transactions-American Society of Mechanical Engineers Journal of Fluids Engineering, 1997, 119: 248-262. [10] VOKE P R. Flow past a square cylinder: test case LES2[J]. Direct and Large Eddy Simulation Ⅱ, Spring, 1997, 5: 335-373 [11] GRIGORIADIS D, BARTZIS J, GOULAS A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632. [12] 张伟,葛耀君. 方柱绕流粒子图像测速试验与数值模拟[J]. 同济大学学报:自然科学版,2009,37(7): 857-861,892. ZHANG Wei, GE Yaojun. Particle image velocimetry study and numerical simulation of turbulent near wake of square cylinder[J]. Journal of Tongji University: Natural Science, 2009, 37(7): 857-861, 892. [13] LILLY D K. A proposed modification of the Germano subgrid-scale closure method[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(3): 633-635. [14] CHOI S K. Note on the use of momentum interpolation method for unsteady flows[J]. Numerical Heat Transfer: Part A: Applications, 1999, 36(5): 545-550. [15] NORBERG C. Flow around rectangular cylinders: pressure forces and wake frequencies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1/2/3): 187-196. [16] 周强,曹曙阳,周志勇. 亚临界雷诺数下圆柱体尾流结构的数值模拟[J]. 同济大学学报:自然科学版,2013,41(1): 33-38. ZHOU Qiang, CAO Shuyang, ZHOU Zhiyong. Numerical studies of wake characteristics on a circular cylinder at sub-critical reynolds number[J]. Journal of Tongji University: Natural Science, 2013, 41(1): 33-38. [17] OKA S, ISHIHARA T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(11): 548-559. [18] NORBERG C. An experimental investigation of the flow around a circular cylinder: influence of aspect ratio[J]. Journal of Fluid Mechanics, 1994, 258: 287-316.1 控制方程与建模
1.1 控制方程
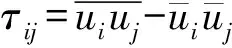
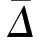
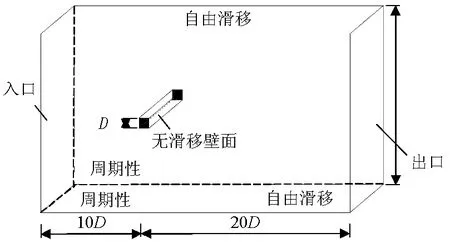
1.2 建模与数值算法



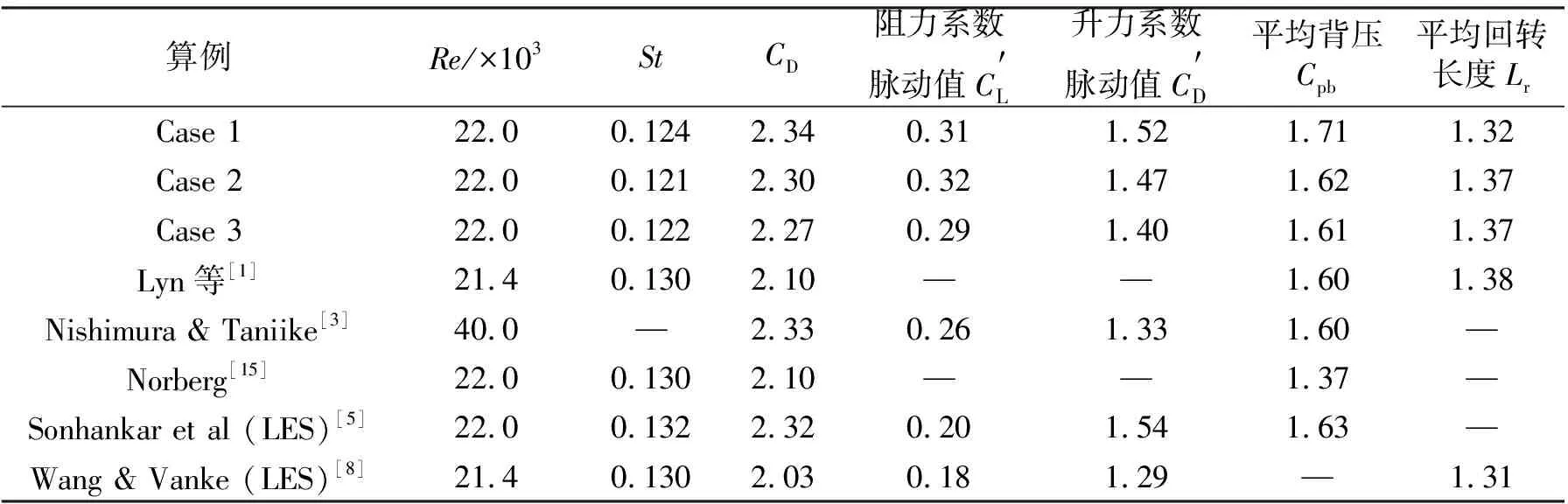
2 数值验证
3 结果与讨论
3.1 气动力特性



3.2 流场特性

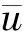


4 结 论

