最大度为5的简单图的2-距离列表染色*

卜月华, 王丽霞

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 金华 321004)

0 引 言

对于图的2-距离色数,1977年,Wegner[1]提出了关于其上界的一个著名的猜想:

猜想1[1]对最大度为Δ的平面图G,有:

Wegner还给出了:若猜想1成立,则上界是可达的.Tomassen利用图的分解和四色定理证明了猜想1对于Δ=3的情况成立,但是目前对于Δ≥4的情况仍未解决.

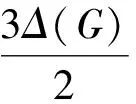
文献[3]给出下列结论：

定理1[3]对最大度为Δ≥8 821且g(G)≥6的平面图G,有χ2(G)≤Δ(G)+2.

文献[4]将定理1改进到以下结论：

定理2[4]对最大度为Δ≥18且g(G)≥6的平面图G,有χ2(G)≤Δ(G)+2.

文献[7]证明下面的定理:

定理3[7]对最大度Δ=4的图G,下列结论成立:

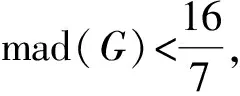
文献[8]研究了Δ(G)=5的图的2-距离染色,有下列结论:

定理4[8]对最大度Δ=5的简单图G,有:

笔者改进了定理 4中4)的结果,主要得到下列结果:

定理5对最大度Δ≤5的简单图G,有:

1 定理 5 的证明

对于G的一个2-距离染色(或G的部分2-距离染色)c,设V1⊆V(G),记c(V1)={c(v)|v∈V1}.用F(v)表示顶点v的禁用色集合,显然有F(v)=c(N2(v)),则|F(v)|≤|N2(v)|≤|D(v)|.由于定理5的2个结果相互独立,因此,可作为2个引理来证明.

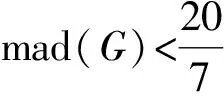
性质1δ(G)≥2.

证明 反证法.若存在1-点v,记uv∈E(G),则根据图G的极小性知,G′=G-v有一个L-2-距离染色c′.因为|F(v)|≤|D(v)|=d(u)≤Δ(G),所以可令c(v)∈L(v)c(N2(v)),u∈V(G-v),c(u)=c′(u),从而G是一个L-2-距离可染的.矛盾.性质1证毕.

性质2k-点(2≤k≤4)至多与k-2个2-点相邻.

证明 设k-点v与k-1个2-点相邻(不妨设d(v1)=d(v2)=…=d(vk-1)=2,d(vk)≥3),则由图G的极小性知,G′=G-v是L-2-距离可染的.擦去v1,v2,…,vk-1的颜色并进行重染.因为|F(v)|≤Δ(G)+k-1≤8,所以可以将v染好.此时|F(vi)|≤Δ(G)+1+1≤7(1≤i≤k-1).因此,可依次染好v1,v2,…,vk-1.从而G是L-2-距离可染的.矛盾.性质2证毕.

性质3若3-点v与1个2-点v1相邻,则v的另外2个邻点v2,v3满足d(v2)+d(v3)≥9.

证明 反证法.假设d(v2)+d(v3)<9,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v的颜色并进行重染.由于d(v2)+d(v3)<9,所以|F(v)|≤d(v2)+d(v3)+1≤8+1=9,从而可以将顶点v染好.此时,|F(v1)|≤Δ(G)+3≤8,所以G是L-2-距离可染的.这与G是引理1的反例矛盾.性质3证毕.

下面利用权转移的方法证明G是不存在的,从而完成引理1的证明.给每个顶点v定义初始权μ(v)=d(v),则

(1)

下面定义转权规则:

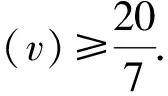
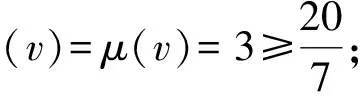
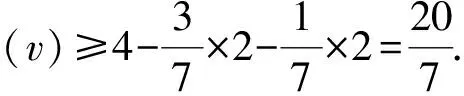
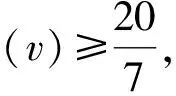
与式(1)矛盾.引理 1 证毕.

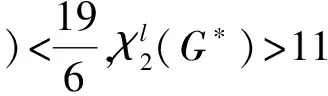
性质4δ(G)≥2.

证明 与性质1的证明一样.故略.

性质5k-点(2≤k≤5)至多与k-2个2-点相邻.

证明 与性质2的证明类似.故略.

性质6若3-点v与1个2-点v1相邻,则v的另外2个邻点v2,v3都是Δ-点.

证明 反证法.若v2,v3中至少有一个(Δ-1)-点,不妨设d(v2)≤Δ(G)-1,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v的颜色并进行重染.由于d(v2)+d(v3)≤9,从而|F(v)|≤d(v2)+d(v3)+1≤9+1=10,所以可以将顶点v染好.此时,|F(v1)|≤Δ(G)+3≤8,所以也可以将v1染好.从而G是L-2-距离可染的.这与G的假设矛盾.性质6证毕.

性质7设3(0)-点v的邻域为N(v)={v1,v2,v3},则

1)若d(v1)=d(v2)=d(v3)=3,则d(vi1)+d(vi2)≥9(i=1,2,3);

2)若d(v1)=d(v2)=3,d(v3)=4,则d(v11)+d(v12)+d(v21)+d(v22)≥18;

3)若d(v1)=d(v2)=3,d(v3)=5,则d(vi1)+d(vi2)≥8(i=1,2).

证明 1)若d(vi1)+d(vi2)(i=1,2,3)中至少有1个小于9,不妨设d(v11)+d(v12)≤8,则由图G的极小性知,对于G′=G-vv1的列表配置L,G′是L-2-距离可染的.擦去v,v1的颜色并进行重染.因为|F(v1)|≤d(v11)+d(v12)+2≤10,所以可令c(v1)∈L(v)c(N2(v1),从而可以将v1染好.此时,v的禁用色至多为9,所以可以将v染好.因此，G是L-2-距离可染的.矛盾.

2)若d(v11)+d(v12)+d(v21)+d(v22)≤17,则d(v11)+d(v12)和d(v21)+d(v22)中至少有1个不超过8,不妨设d(v11)+d(v12)≤8.由图G的极小性知,G′=G-vv1是L-2-距离可染的.擦去v,v1的颜色并进行重染.因为|F(v1)|≤d(v11)+d(v12)+2≤8+2=10,|F(v)|≤4+3+2=9,所以可以依次染好v1,v,从而图G是L-2-距离可染的.矛盾.

3)不妨设d(v11)+d(v12)≤7,由图G的极小性知,G′=G-vv1是L-2-距离可染的.擦去v,v1的颜色并进行重染.因为|F(v)|≤d(v3)+3+2=10,所以可以将v染好.此时,因为d(v11)+d(v12)≤7,所以|F(v1)|≤7+3=10,从而可以将v1染好.这与G是引理2的极小反例矛盾.性质7证毕.

性质8若4-点v与2个2-点v1,v2相邻,则d(v3)+d(v4)≥9,且4(2)-点不与4(2)-点相邻.

证明 若d(v3)+d(v4)≤8,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2的颜色并进行重染.因为|F(v)|≤8+2=10,所以可以将v染好.此时,|F(vi)|≤Δ(G)+4≤9(i=1,2),从而可以将v1,v2染好.与G是引理2的极小反例矛盾.

若4(2)-点v与1个4(2)-点v3相邻,记与v3相邻的2个2-点为v31,v32.由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v3,v31,v32的颜色并进行重染.先讨论顶点v和v3的禁用色.因为|F(v)|≤Δ(G)+1+2+1≤9,|F(v3)|≤Δ(G)+2+2≤9,所以可以将v和v3染好.此时,2-点v1,v31和v32的禁用色分别不超过Δ(G)+4,Δ(G)+3,Δ(G)+3,从而G是L-2-距离可染的.矛盾.性质8证毕.

性质94(1)-点v至多与1个4(2)-点相邻.若4(1)-点v与1个4(2)-点相邻,记此点为v2,则d(v3)+d(v4)≥9.

证明 设4-点v的邻域为N(v)={v1,v2,v3,v4}.若v1是2-点,v2,v3是4(2)-点,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3及N(v2),N(v3)中2-点的颜色并进行重染.因为|F(v)|≤Δ(G)+3≤8,|F(vi)|≤Δ(G)+2+1≤8(i=2,3),所以可以将v,v2,v3依次染好.此时,|F(v1)|≤Δ(G)+4≤9,因此,可以将v1重新染好.最后,因为N(vi) (i=2,3)中2-点的禁用色至多为Δ(G)+3≤8(若N(v2)和N(v2)中有2个2-点的距离小于等于2,则这2个2-点的可用色相应增加),所以可以将N(v2)和N(v3)中的2-点重染好,从而G是L-2-距离可染的.这与G的假设矛盾.

设4(1)-点v相邻2-点v1和4(2)-点v2,但是d(v3)+d(v4)≤8,记v2的2个2-邻点为v21,v22.由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v21,v22的颜色并进行重染.因为|F(v)|≤d(v3)+d(v4)+2≤8+2=10,|F(v2)|≤Δ(G)+2+2≤9,所以可以依次染好v,v2.此时,|F(v1)|≤Δ(G)+4≤9,因此可以将v1染好.因为v21,v22的禁用色都不超过Δ(G)+3≤8,所以v21,v22可以被染好，从而G是L-2-距离可染的.矛盾.因此,d(v3)+d(v4)≥9.性质9证毕.

性质101)4(1)-点v至少与1个4+-点相邻;当4(1)-点v恰好与2个3(0)-点v2,v3相邻时,v2和v3只能是i-型3(0)-点和j-型3(0)-点,其中i+j≤2.

2)若4(1)-点v与2个1-型的3(0)-点v2,v3相邻,其中v2,v3不同于v的邻点分别记为v2i,v3i(i=1,2),d(v21)=d(v31)=3,则d(v22)=d(v32)=Δ.

证明 1)若4(1)-点v与3个3-点v2,v3,v4相邻,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去顶点v的颜色并进行重染.因为|F(v)|≤3×3+1=10,|F(v1)|≤Δ(G)+3=8,所以可以依次染好v,v1,从而G是L-2-距离可染的.矛盾.

若与4(1)-点v相邻的2个3(0)-点中一个是1-型的3(0)-点v2,另一个是2-型的3(0)-点v3,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3的颜色并进行重染.因为|F(v)|≤Δ(G)+1+2+2≤10,所以可以将v染好.此时|F(v2)|≤Δ(G)+3+2≤10,|F(v3)|≤3+3+2=8,故可以依次将v2,v3染好.最后,因为|F(v1)|≤Δ(G)+4≤9,所以图G是L-2-距离可染的.矛盾.其他情况类似可证.

2)当4(1)-点v与2个1-型的3(0)-点v2,v3相邻时,若d(v22)+d(v32)<2Δ,则可设d(v22)≤Δ-1.由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3的颜色并进行重染.因为|F(v)|≤Δ(G)+1+2+2=10,所以可以将v染好.此时,|F(v3)|≤Δ(G)+3+2=10,|F(v2)|≤Δ(G)-1+2+3≤9,故可以依次染好v3,v2.最后,因为|F(v)|≤Δ(G)+4≤9,所以图G是L-2-距离可染的.矛盾.性质10证毕.

性质11设v为4(0)-点,N(v)={v1,v2,v3,v4},则N(v)中至多有3个4(2)-点.若N(v)中恰好有3个4(2)-点,则v的另一个邻点v4及vi(i=1,2,3)的另一个邻点都是Δ-点.

证明 若4(0)-点v与4个4(2)-点v1,v2,v3,v4相邻,则由图G的极小性知,G′=G-v是L-2-距离可染的.擦去v1,v2,v3,v4及N2(v)中2-点的颜色并进行重染.由于|F(vi)|≤Δ(G)+2≤7(i=1,2,3,4),所以可以依次染好v1,v2,v3,v4.此时,|F(v)|≤4×2=8,故也可以将v染好.最后,由于N2(v)中2-点的禁用色都不超过Δ(G)+3≤8,所以可以将未着色的2-点都染好，从而G是L-2-距离可染的.矛盾.

若N(v)中恰好有3个4(2)-点,但是v的另一个邻点v4或vi(i=1,2,3)的另一个邻点中有一个不是Δ-点,不妨设d(v4)≤Δ(G)-1.由图G的极小性知,G′=G-v是L-2-距离可染的.擦去v1,v2,v3和N(vi)(i=1,2,3)中2-点的颜色并进行重染.因为|F(vi)|≤Δ(G)+2≤7(i=1,2,3),所以可以依次染好v1,v2,v3.此时,|F(v)|≤(Δ(G)-1)+2×3≤10,故可以染好v.最后,由于N(vi)(i=1,2,3)中2-点的禁用色至多为Δ(G)+3≤8,所以可以将它们都染好,从而图G是L-2-距离可染的.这与图G的假设矛盾.其他几种情况类似可证.性质11证毕.

性质12若5-点v与3个2-点相邻,则d(v4)+d(v5)≥8,即v4,v5是5-点与3+-点或者都是4+-点,且v不再与5(3)-点、3(1)-点、4(2)-点、i-型的3(0)-点相邻(i=1,2).

证明 设5(3)-点v的2-邻点分别为v1,v2,v3.

若d(v4)+d(v5)<8,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3的颜色并进行重染.因为|F(v)|≤d(v4)+d(v5)+3≤7+3=10,所以可以将v染好.此时,|F(vi)|≤Δ(G)+3≤8(i=1,2,3),从而G是L-2-距离可染的.这与G的假设矛盾.

若5(3)-点v与5(3)-点v4相邻,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v1,v2,v3,v4和N(v4)中2-点的颜色并进行重染.由于|F(v)|≤Δ(G)+3+1≤9,|F(v4)|≤Δ(G)+4≤9,所以可以依次将v和v4染好.此时,|F(vi)|≤Δ(G)+3≤8,故可以将vi染好(i=1,2,3).最后,因为N(v4)中每个2-点的禁用色至多是Δ(G)+3≤8,从而G是L-2-距离可染的.这与G的假设矛盾.

类似地,可以证明5(3)-点v不与4(2)-点、3(1)-点相邻.

下面将证明5(3)-点v不与i-型的3(0)-点相邻(i=1,2).

设5(3)-点v与1-型的3(0)-点v4相邻,为方便,记v4的3-邻点为v41,v的2-邻点为v1,v2,v3.由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v4,v2,v3的颜色并进行重染.因为|F(v)|≤Δ(G)+3+2≤10,|F(v4)|≤Δ(G)+3+1≤9,所以可以染好v和v4.此时,|F(vi)|≤Δ(G)+3≤8(i=1,2,3),从而G是L-2-距离可染的.矛盾.同样可以证明5(3)-点不与2-型3(0)-点相邻.性质12证明.

性质131)5(2)-点v至多与1个4(2)-点或3(1)-点相邻且5(2)-点不同时与3(1)-点和4(2)-点相邻;

2)当5(2)-点v与1个4(2)-点或3(1)-点相邻时,有d(v4)+d(v5)≥8;

3)5(2)-点不同时与3(1)-点和i-型3(0)-点(i=1或2)相邻.

证明 设与5(2)-点v相邻的2个2-点为v1,v2.

1)若5(2)-点v相邻2个4(2)-点v3,v4,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3,v4及N(v3),N(v4)中2-点的颜色.由于|F(v)|≤Δ(G)+4≤9,|F(vi)|≤Δ(G)+3≤8(i=3,4),|F(vi)|≤Δ(G)+1(i=1,2),所以可以依次染好v,v3,v4,v1,v2.此时,N(v3)中2-点的禁用色至多为Δ(G)+3≤8,故可以将N(v3)中的2-点染好.最后,因为N(v4)中的2-点的禁用色至多为Δ(G)+3≤8,所以仍可以将N(v4)中的2-点染好.因此,G是L-2-距离可染的.矛盾.同样可证其他几种情况.

2)设5(2)-点v相邻1个4(2)-点或3(1)-点v3且d(v4)+d(v5)≤7,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v1,v2,v3及N(v3)中2-点的颜色.因为|F(v)|≤d(v4)+d(v5)+3≤7+3=10,|F(v3)|≤Δ(G)+2+2≤9,|F(vi)|≤Δ(G)+2≤7(i=1,2),所以可以依次染好v,v3,v1,v2.此时,因为N(v3)中的每个2-点的禁用色至多是Δ(G)+3≤8,所以可以将N(v3)中的2-点染好,从而G是L-2-距离可染的.矛盾.

3)若5(2)-点v相邻1个3(1)-点v3和1个1-型的3(0)-点v4,则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3,v4及N(v3)中2-点的颜色.因为|F(v)|≤Δ(G)+3+2=10,|F(v4)|≤Δ(G)+4≤9,|F(v3)|≤Δ(G)+2≤7,|F(vi)|≤Δ(G)+1(i=1,2),所以可以依次染好v,v4,v3,v1,v2.最后,因为N(v3)中2-点的禁用色至多为Δ(G)+3≤8,从而G是L-2-距离可染的.这与G的假设矛盾.性质13证毕.

性质145(1)-点v至多与2个3(1)-点相邻.当5(1)-点v与2个3(1)-点v2,v3相邻时,d(v4)+d(v5)≥8,即v4,v5都是4+-点或者是5-点与3+-点.

证明 5(1)-点至多与2个3(1)-点相邻的证明与5(2)-点至多与1个3(1)-点相邻的证明类似.故略.

若5(1)-点v与2个3(1)-点v2,v3相邻且d(v4)+d(v5)≤7(为方便,记v的2-邻点为v1),则由图G的极小性知,G′=G-v1是L-2-距离可染的.擦去v,v2,v3及N(v2),N(v3)中2-点的颜色.因为|F(v)|≤d(v4)+d(v5)+3≤7+3=10,|F(vi)|≤Δ(G)+1+2=8(i=2,3),|F(v1)|≤Δ(G)+2≤7,所以可以先染好v,再染好v2,v3,v1.此时,N(v2),N(v3)中2-点的禁用色至多是Δ(G)+3≤8,所以G是L-2-距离可染的.这与G的假设矛盾.性质14证毕.

性质155(0)-点至多与4个3(1)-点相邻.

证明 若5(0)-点v与5个3(1)-点相邻(为方便,记v1,v2,v3,v4,v5为v的5个3(1)-邻点,vi1为vi的2-邻点(i=1,2,3,4,5)),则由图G的极小性知,G′=G-v是L-2-距离可染的.擦去vi,vi1(i=1,2,3,4,5)的颜色并进行重染.因为|F(vi)|≤Δ(G)+1≤6(i=1,2,3,4,5),所以可以依次染好v1,v2,v3,v4,v5.此时,因为|F(v)|≤2×5=10,所以可以将v染好.最后,因为|F(vi1)|≤Δ(G)+3≤8(i=1,2,3,4,5),所以可以染好N2(v)中的2-点v11,v21,v31,v41,v51,从而图G是L-2-距离可染的.矛盾.性质15证毕.

接下来利用权转移的方法证明G不存在,从而完成引理2的证明.给每个点一个初始权μ(v)=d(v),则

(2)

下面定义转权规则:

2)d(v)=3.由性质5知,v至多相邻1个 2-点.

②v是3(0)-点.

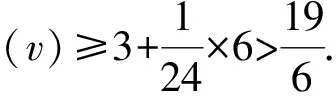
3)d(v)=4.由性质5知,v至多与2个2-点相邻.考虑下面几种情况：

②v是4(1)-点.由性质10知,v至少与1个 4+-点相邻.

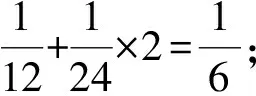
③v是4(0)-点.由性质11知,v至多与3个4(2)-点相邻.

4)d(v)=5.由性质5知,v至多相邻3个2-点.考虑下列情况:

①v是5(3)-点.由性质12知,d(v4)+d(v5)≥8.

②v是5(2)-点.由性质13中的1)知,v至多与1个3(1)-点或4(2)-点相邻.

③v是5(1)-点.由性质14知,v至多与2个3(1)-点相邻.

与式(2)矛盾.引理2证毕.

综合引理1、引理2的结论,完成定理5的证明.

2 结 语

参考文献：

[1]Wegner G.Graphs with given diameter and a coloring problem[R].Dortmund:University of Dortmund,1977.

[2]Lih K W,Wang W F,Zhu X.Coloring the square of aK4-minor free graph[J].Discrete Math,2003,269(1/2/3):303-309.

[4]Borodin O V,Ivanova A O.2-distance (Δ+2)-coloring of planar graphs with girth six andΔ≥18[J].Discrete Math,2009,309(23/24):6496-6502.

[5]Bonamy M,Lévêque B,Pinlou A.Graphs with maximum degreeΔ≥17 and maximum average degree less than 3 are list 2-distance (Δ+2)-colorable[J].Discreten Math,2014,317:19-32.

[6]Cranston D W,krekovski R.Sufficient sparseness conditions forG2to be (Δ+1)-choosable whenΔ≥ 5[J].Discrete Appl Math,2014,162(10):167-176.

[7]Cranston D W,Erman R,krekovski R.Choosability of the square of a planar graph with maximum degree four [J].Australas J Combin,2014,59(1):86-97.

[8]Bu Yuehua,Lü Xia,Yan Xiaoyan.The list 2-distance coloring of a graph withΔ(G)=5[J].Discrete Mathematics,Algorithms and Applications,2015,7(2):1550017(11).