隔板法在排列组合中的应用

■河南省虞城县高级中学 何海涛

排列组合是高考的必考内容,它联系生活实际、题型多变、解法灵活、能力要求高,但得分率低。而排列组合中的分配问题,是排列组合问题中的重点与难点 ,对于排列组合中涉及相同物品的分配或名额分配的问题,若采用隔板法,则能起到事半功倍的效果。

一、问题的提出

将n个相同的元素分到m个(n≥m)不同盒中,有多少种不同的分法?

模型1.要求每盒非空

例1 某校准备组建一个由12人组成的篮球队,这12个人来自高一年级10个班级,每个班至少1人,问分配方案共有多少种。

解析:将问题抽象为:12个相同的小球,分配给10个不同的班级,也就是将12个小球排成一排,在其两两之间的11个空中任取9个插上隔板,这样就将12个小球分成了10组,分隔成的10个小组的球的个数与名额分配数相等,则隔板插入的方法数就等于名额分配方案数,共有C911=55(种)分法。

模型2.要求盒子可空

例2 将8个相同的小球放入4个不同的盒子中,盒子可空,有多少种不同的方法?

解析:首先设想每个盒子中借来1个球,共用去4个球,若某盒最后分得结果为n个(n≥1),则代表原来8个相同的小球分入该盒n-1个球,则原问题等价于“将12个相同的小球放入4个不同盒子中,每盒至少一个小球”,由例1知方法数为C311=165。

方法总结如下:

模型1:将n个相同的元素分装到m个不同盒中(n≥m),每个盒子至少1个元素,方法数为Cm-1n-1。

模型2:将n个相同的元素分装到m个不同的盒中,盒子可空,则方法数为Cm-1n+m-1。

二、应用举例

1.要求每盒至少n个元素

例3 将20本相同的书分给4名学生,要求每名学生至少3本,有多少种不同的分法。

解法1:可以将问题转化为模型1,首先每人分得相同的2本,然后从剩下的12本按照模型1的方法分配分给4个人,则有C311=165(种)分法。

解法2:可以将问题转化为模型2,首先每人分得相同的3本,然后从剩下的8本按照模型2的方法分配分给4个人,则有C4-18+4-1=C311=165(种)分法。

2.要求每盒分别有n1,n2…,nm个元素

例4 某校准备参加今年高中的数学联赛,把16个选手名额分配到三(1)、三(2)、三(3)、三(4)四个教学班,每班的名额不少于该班的序号数,则不同的分配方案共有多少种?

解法1:可以将问题转化为模型1,首先三(2)班分得1个名额,三(3)班分得2个名额,三(4)班分得3个名额,再将剩余的10个相同的名额分配给4个班级,每个班级至少有1个名额,按照模型1的方法共有C39=84(种)分配方案。

解法2:可以将问题转化为模型2,首先三(1)班分得1个名额,三(2)班分得2个名额,三(3)班分得3个名额,三(4)班分得4个名额,再将剩余的6个相同的名额分配给4个班级,按照模型2的方法共有C4-16+4-1=C39=84(种)分配方案。

3.求不定方程非负整数解的个数

例5 求不定方程x+y+z=12非负整数解的个数。

解析:将x、y、z分别看成是x个1,y个1,z个1组成,则共有12个1,问题转化为模型2,将12个1分给3个对象x、y、z,允许有空,则不同的分配方法有ffff93=91(种),不定方程非负整数解的个数为91个。

例6 求(x1+x2+…+x5)10的展开式中共有多少项。

解析:(x1+x2+…+x5)10的展开式中的通项公式为k3+k4+k5=10(k1、k2、k3、k4、k5∈Z)。

则该问题转化为求不定方程k1+k2+k3+k4+k5=10的非负整数解的个数,根据例5不难得到方程非负整数解的个数为C414,故(x1+x2+…+x5)10的展开式中共有C414项。

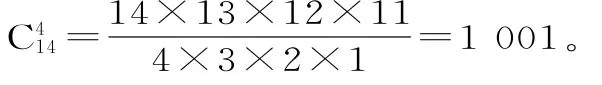
所以,(x1+x2+…+x5)10的展开式中共有1001项。