近水面状态有限长圆柱壳受迫振动的输入功率流和声辐射特性

王鹏 李天匀 朱翔 郭文杰

摘要： 基于声固耦合模型，采用波传播方法分析近水面状态有限长圆柱壳受迫振动的输入功率流和声辐射特性，并考虑了自由液面的影响。通过与有限元仿真结果进行对比分析，验证了该方法的正确性。当圆柱壳接近自由液面时，自由液面的存在致使水下圆柱壳输入功率流和声辐射特性的峰值频率向高频偏移，且响应幅值也略有增大。随着潜深的增大，自由液面对圆柱壳输入功率流特性的影响逐渐减小。当潜深大于5倍半径时，自由液面对耦合系统输入功率流的影响可以忽略，但其对耦合系统声辐射特性的影响不可忽略。关键词： 船舶振动； 近水面状态圆柱壳； 自由液面； 输入功率流； 虚源法

中图分类号： U661.44； O427.1文献标志码： A文章编号： 10044523（2017）04059607

DOI：10.16385/j.cnki.issn.10044523.2017.04.010

引言

自由液面广泛存在于工程实际应用中。自由液面的存在将致使流场形成有限域，它对声波的反射作用也会导致有限域内圆柱壳振动与声辐射特性较无限域状态存在明显差异，且使得声场分布特性更为复杂。因此，研究自由液面对圆柱壳振动与声辐射特性的影响是十分重要的。

国内外许多学者已针对半无限域内圆柱壳的声辐射特性进行了分析研究，但主要针对二维圆柱殼结构。Skidan[1]基于边界积分方法分析推导了半无限域内圆柱壳的声辐射特性，并分别考虑了自由液面和刚性壁面的影响。Chang[2]基于Flügge壳体理论和近似辐射条件，将半无限域内圆柱壳声场耦合问题转变成一个边界值问题，并通过双极子坐标变换求解了耦合系统的辐射声压。Ye[3]基于波传播方法探讨了存在刚性壁面条件下浸没圆柱壳的特殊声振特性。李天匀[4]基于波传播方法分析推导了有限潜深状态下二维圆柱壳辐射声压的近似表达式，并探讨了自由液面对结构声辐射特性的影响。

针对有限域内有限长圆柱壳的声振特性，国内外学者也开展了相关研究。Ergin[5]基于三维水动力数学模型方法，分析了自由液面和刚性壁面对水下圆柱壳自振特性的影响。基于有限元方法，王宗利[6]对有限潜深状态下圆柱壳的自振特性展开了数值分析，并计入了流体静压的影响。基于有限元软件ANSYS，刘佩[7]通过数值仿真分析了自由液面和刚性壁面对圆柱壳固有频率特性的影响。王鹏[8]采用波传播方法分析了近水面状态下圆柱壳的固有振动特性，并探讨了自由液面对圆柱壳模态频率特性的影响。目前，针对有限域内有限长圆柱壳的声振特性研究主要侧重于圆柱壳的自由振动特性，较少涉及圆柱壳的受迫振动和声辐射特性。

本文基于波传播方法建立近水面状态下有限长圆柱壳声场耦合振动模型，并考虑自由液面的影响，进而分析圆柱壳受迫振动的输入功率流和声辐射特性。通过与有限元方法进行对比分析，对本文理论分析方法的正确性进行验证，随后探讨了自由液面、潜深等对近水面状态下有限长圆柱壳输入功率流和声辐射特性的影响。

1理论分析〖*4〗1.1研究对象近水面状态下有限长圆柱壳结构如图1所示。圆柱壳长度为2L，半径为R，厚度为h。壳体材料的密度为ρs，弹性模量为E，泊松比为μ。圆柱壳轴线与自由液面平行，且距离为H，定义为潜深。流体密度为ρf。柱坐标系如图1所示，z， θ， r分别表示圆柱壳的轴向，周向和径向。圆柱壳两端分别简支在半无限长的刚性声障板上。

图1近水面状态有限长圆柱壳结构示意图

Fig.1Sketch of a finite cylindrical shell submerged near the free surface第4期王鹏，等： 近水面状态有限长圆柱壳受迫振动的输入功率流和声辐射特性振 动 工 程 学 报第30卷1.2壳体振动方程

采用Flügge理论描述壳体振动方程Lu

v

w=1-μ2R2E′h0

0

fr-pr=R（1）式中E′=E（1+iξ），ξ为结构阻尼因子，L为微分算子矩阵，具体元素如下：

L11=R22z2+1-μ2（K+1）2θ2-ρsR2（1-μ2）E2t2，

L12=L21=1+μ2R2zθ，L13=L31=-KR33z3+

1-μ2KR3zθ2+μRz，L22=1-μ2（3K+

1）R22z2+2θ2-ρsR2（1-μ2）E2t2，L23=L32=

θ-3-μ2KR23z2θ，L33=1+K+KR44z4+

2KR24〖〗z2θ2+K4θ4+2K2θ2+ρsR2（1-μ2）E2t2。

厚度因子K=h2/（12R2），u， v， w分别表示轴向、周向和径向的壳体位移。p|r=R是壳体表面的流体声压，反映了流体对结构的反作用力，fr表示外激励力。当壳体受对称载荷激励时，壳体受迫振动响应是结构对称模态响应的叠加，当圆柱壳受非对称载荷激励，则壳体振动响应应为对称和非对称模态响应的叠加。为简化分析，考虑壳体受对称载荷激励，如图1所示。

基于波传播方法，可以假设圆柱壳位移具有如下展开式（略去时间简谐项eiωt）：u=∑+∞m=0∑+∞n=0Umncos（nθ）sinkmz

v=∑+∞m=0∑+∞n=0Vmnsinnθcoskmz

w=∑+∞m=0∑+∞n=0Wmncosnθcoskmz（2）式中m， n分别为轴向和周向模态阶数，km为轴向波数，可根据壳体边界条件确定[9]。假设壳体两端简支，kmL=（2m+1）π/2。

1.3流体声压

假设流体为理想声介质，则流体声压满足声学波动方程2p-1c2f2pt2=0（3）式中cf为流体声速。

自由液面对声波的反射作用使得声场形成半无限域，也致使圆柱壳的声场分布特性更加复杂，本文采用虚源法处理自由液面的影响，如图2所示。忽略圆柱壳结构的声散射效应，则流体中声场包括两部分：一部分是由于结构振动产生的辐射声场，其声压用pr表示；另一部分是由于自由液面对声波的反射所形成的反射声场，即虚源的辐射声场，其声压用pi表示。因而，在半无限域声场中，流体声压可以表述为

图2虚源法示意图

Fig.2Sketch of the image methodp=pr+pi（4）

采用分离变量法求解式（3），可以得到流体声压的表达式pr=∑∞m=0∑∞n=0prmn（z）H（2）n（krr）cos（nθ）

pi=∑∞m=0∑∞n=0pimn（z）H（2）n（krr′）cos（nθ′） （5）式中kr为径向波数，k2r=k2f-k2m，kf=ωcf。H（2）n（）为n阶Hankel函数。r′和θ′为虚源坐标系的径向和周向。

忽略流体的重力效应和自由液面的表面波动效应，则流体声压在自由液面处满足声压释放条件

pr，θ，zfree surface=0（6）

在自由液面上的任意一点，r=r′，θ′=π-θ。

基于graf加法定理[10]，可以建立虚源声场与本体辐射声场的映射关系H（2）n（krr′）cos（nθ′）=

∑a=-∞（-1）aH（2）n-a（2krH）Ja（krr）cos（aθ），r≤2H

∑a=-∞（-1）aJn-a（2krH）H（2）a（krr）cos（aθ），r≥2H（7）式中a为加法定理的级数下标，Jn（）表示n阶第一类Bessel函数。

流体与圆柱壳结构始终保持接触，则辐射声压与壳体径向振速在交界面处满足声振连续条件-1iρfωpr〖〗rr=R=wt（8）将式（5）和（2）代入上式，并进行Fourier变换，可得rmn（λ）=ρfω2krH（2）′n（krR）m（λ）Wmn（9）式中mλ=∫L-Lexp（iλz）cos（kmz）dz。

1.4外激励力

假设圆柱壳受径向点激励力作用，则外激励力可以表述成fr=F0Rδ（z-z0）δ（θ-θ0）（10）式中F0为激励力幅值，z0和θ0分别为激励点的轴向和周向坐标，δ（）为狄拉克函数。壳体受如图1所示的对称载荷激励，则z0=0，θ0=0。

依波传播方法，对外激励力做级数展开

fr=∑+∞〖〗m=0∑+∞n=0frmncosnθcoskmz（11）

式中frmn=εnFo/（2πLR）。当n=0时，εn=1；当n≥1时，εn =2。

1.5声固耦合振动方程

将式（2），（4），（5），（11）代入壳体振动方程，消去轴向位移和周向位移并进行正交化处理，可得近水面状态下圆柱壳声场耦合振动方程

ZMmnWmn+∑+∞p=0ZmnpqWpn=frmn（12）

式中机械位移阻抗ZMmn=EhR2（1-μ2）II33，II33=（T11T22-T12T21）det（T），T为（m， n）阶模态下的系数矩阵，其各元素为：

T11=-k2mR2-n21+K1-μ/2+Ω2，T12=

-kmRn1+μ/2，T21=T12，T13=-kmRν1-

Kk3mR3+n2KkmR1-μ/2，T31=-T13，T32=

-T23，T22=-k2mR2（1+3K）1-ν1/2-n2+

Ω2，T23=-n-Knk2mR23-μ/2，T33=1+K-

2Kn2+Kk2mR2+n22-Ω2，无量纲频率Ω=ω/ωring，壳体环频率ωring=ER2ρs1-μ2。辐射位移阻抗，Zmnpq=Zrmpn+Zimpn，体现了（m，n）阶振动模态与（p，q） 阶振动模态的耦合作用。Zrmpn和Zimpn分别表示辐射声和反射声的位移阻抗，Zrmpn=ρfω2πL·∫∞-∞H（2）n（krR）krH（2）′n（krR）m（λ）p（λ）dλ，Zimpn=ρfω2πL·

∑q=0∫∞-∞（-1）q+1ΔJn（krR）krH（2）′q（krR）m（λ）p（λ）dλ， Δ=

H（2）q-n（2krH）+（-1）nH（2）q+n（2krH）。Zrmpn体现了声场圆柱壳耦合作用，而Zimpn反映了自由液面的影响。

1.6输入功率流

根据输入功率流的定义，点激励力作用下近水面状态有限长圆柱壳的输入功率流可表述为pin=1〖〗2∫SRe（fr）ds（13）式中S为壳体外表面积。

为方便后续数据分析，对输入功率流进行无量化处理Pin=pinF20πρsE（1-μ2）（14）1.7辐射声功率

根据辐射声功率的定义，可以得到近水面状态下有限长圆柱壳流场耦合系统的辐射声功率pv=∫Sp（wt）ds（15）式中（）表示复共轭，S表示壳体外表面积。

定义辐射声功率级Lpv=10lg（pvC0）（16）式中C0为辐射声功率的参考值，C0=0.67×10-18 W。

2方法验证2.1流场圆柱壳耦合系统参数本文选取的声场圆柱壳耦合模型参数如表1所示。表1有限潜深状态下圆柱壳流场耦合模型参数

Tab.1Parameters for the coupled system of a cylindrical shell submerged near the free surface壳体壳体材料流体外力长度L/

m半径R/

m厚度h/

m密度ρs/

（kg·m-3）泊松比

μ彈性模量E/

Pa阻尼因子

ξ密度ρf/

（kg·m-3）声速cf/

（m·s-1） 幅值

F01.2840.180.00378500.32.06×10110.051025146012.2收敛性分析

输入功率流参数的计算涉及对模态数m， n以及下标q的截断，因此有必要进行理论方法的收敛性分析。假设对m， n和q的最大取值分别为M，N和A，外激励力频率f=150 Hz，圆柱壳潜深H=0.2 m，选取点（z=L/2， θ=π， r=R）的壳体位移级Lw作为评价指标，收敛性分析结果如图3所示。位移级定义，Lw=20lg（w/w0）， w0=1×10-12 m。

图3理论方法收敛性分析

Fig.3Convergence analysis of present method

假设M，N，A均相等且均为MN，然后采用控制变量法分别探讨M，N，A对理论计算结果收敛性的影响。从图3中可以看出，M=N=A=15足以保证计算结果收敛。

2.3理论方法验证

目前尚无关于存在自由液面条件下有限长圆柱壳结构输入功率流特性的研究，无法直接引用文献验证本文方法的正确性。依据输入功率流的定义式可以知道，圆柱壳结构受迫振动的输入功率流特性与壳体的受迫振动响应密切相关。因此，本文选取壳体振动位移为评价指标，并通过与基于有限元软件Patran/Nastran[8]的计算结果进行对比分析以验证本文方法的有效性。假设潜深H=0.5 m，选取点（z=L/2， θ=π， r=R）处的振动位移级进行验证分析，结果如图4所示。

从图4中可以看出，本文计算结果与有限元结果整体吻合较好，壳体振动位移随激励频率的变化规律一致，仅在峰值频率点及共振峰值上略有偏差，但相对误差较小。因此，本文提出的理论分析方法是正确的。

图4本文方法与有限元方法对比验证

Fig.4Validation of the present method3数值计算〖*3〗3.1自由液面对水下圆柱壳输入功率流特性的影响为了探究自由液面对水下圆柱壳输入功率流特性的影响，本文给出了潜深H=0.2 m时圆柱壳输入功率流特性随激励频率的变化关系，并与理想无限域中圆柱壳的输入功率流进行对比分析，如图5所示。

图5自由液面对水下圆柱壳输入功率流特性的影响

Fig.5Effect of free surface on input power flow from a submerged cylindrical shell

从图5可以看出，当圆柱壳靠近自由液面时，自由液面的存在将致使耦合系统输入功率流曲线的峰值频率相应向高频偏移，对共振幅值也略有影响。将流体对结构振动的影响等效为附连水质量，则自由液面的存在将致使水下圆柱壳的附连水质量减少，进而导致水下圆柱壳流场耦合系统的耦合模态频率增大，也会导致圆柱壳受迫振动响应略微增大。上述结论与作者[8]研究自由液面对水下圆柱壳自由振动特性影响所得到的结论相一致，进一步说明了本文方法的正确性。

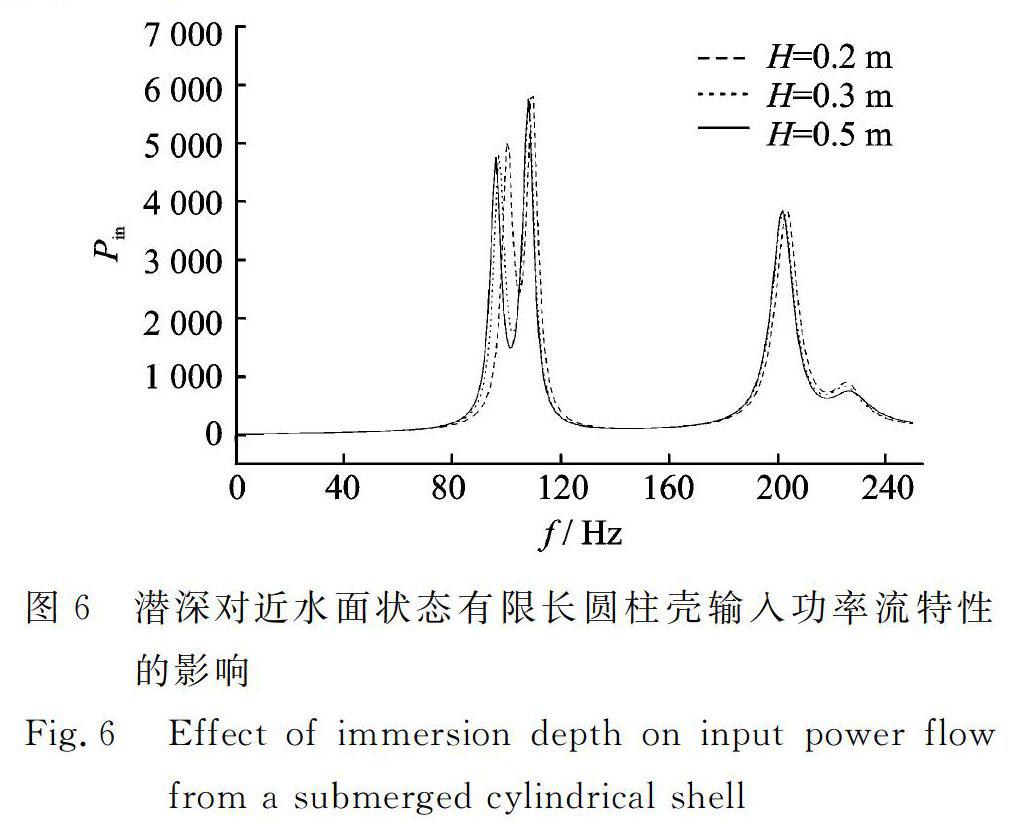
3.2潜深对近水面状态圆柱壳输入功率流特性的影响为了研究潜深对近水面状态圆柱壳输入功率流特性的影响，本文分别给出了H=0.2，0.3，0.5 m条件下圆柱壳输入功率流随激励频率的变化规律，如图6所示。

图6潜深对近水面状态有限长圆柱壳输入功率流特性的影响

Fig.6Effect of immersion depth on input power flow from a submerged cylindrical shell

从图6可以看出，不同潜深条件下圆柱壳输入功率流特性随激励频率的整体变化规律较类似，但在峰值频率和共振幅值上存在差异。随激励频率的增大，圆柱壳受迫振动的平均输入功率流增大，并在耦合模态频率点附近产生共振现象，即出现明显峰值。随着潜深H的增大，圆柱壳输入功率流曲线的峰值频率点向低频偏移，且共振响应幅值也略有变化。因而，当圆柱壳接近自由液面时，随着壳体潜深的增大，耦合模态频率相应地逐渐减小。上述现象表明，随着潜深的增大，自由液面对水下圆柱壳输入功率流特性的影响逐渐减小。此外，潜深对耦合系统振动能量特性曲线不同共振频率的影响程度（如峰值频率偏移量和共振幅值变化量）不尽相同。

从式（12）可知，Zrmn反映了声场圆柱壳耦合作用，而Zimn反映了自由液面的影响。为了探究自由液面对水下圆柱壳受迫振动响应特性的影响机理，本文给出了前五阶模态下辐射阻抗比Zimn/Zrmn随潜深比H/R的变化规律，如图7所示。

图7辐射阻抗比|Zimn/Zrmn|随潜深比H/R的变化

Fig.7Variation of impedance ratio |Zimn/Zrmn| versus immersion depth ratio H/R当潜深较小时，各阶弯曲模态下辐射声阻抗比Zimn/Zrmn相对较大。此时，反射声阻抗Zimn与辐射声阻抗Zrmn大小相近，因而自由液面的影响不可忽略。此外，潜深较小时不同弯曲模态下的阻抗比值大小不一（低阶模态下的阻抗比值较大，而高阶模态下的阻抗比值则相对较小），这说明自由液面对耦合系统耦合模态频率的影响程度不尽相同。随着潜深比H/R的增大，耦合系统各阶辐射阻抗比Zimn/Zrmn均减小并逐渐趋于0。辐射声阻抗Zrmn与潜深H无关，则上述现象说明自由液面的影响随着潜深的增大而逐渐减小。当潜深H≥5R时，耦合系统各阶辐射阻抗比Zimn/Zrmn均已完全收敛于0。此时，反射声阻抗Zimn较辐射声阻抗Zrmn而言是一个小量，因而自由液面的影响可以忽略。此外，辐射声阻抗比值Zimn/Zrmn是无量纲量，受结构几何尺寸影响较小，因此本文结论具有一定的普遍性。

自由液面对水下圆柱壳受迫振动响应特性的影响也可以采用声波衰减理论来解释。反射声阻抗Zimn可以反映自由液面的影响，且与虚源辐射声场密切相关。图7表明，随着潜深H的增大，反射声阻抗Zimn逐渐减小并趋于0。随着潜深H的增大，虚源辐射声波传播距离增长，声波衰减效应越来越明显，虚源辐射声波对耦合系统声场的贡献也逐渐减小，并最终可以忽略。

3.3自由液面对近水面状态圆柱壳声辐射特性的影响为了探究自由液面对近水面状态下圆柱壳声辐射特性的影响，本文给出了H=0.2，0.3，0.9，1.5 m条件下圆柱壳辐射声功率随激励频率的变化规律，如图8所示。

从图8可以看出，不同潛深条件下圆柱壳辐射声功率（如峰值频率点和共振响应幅值）存在明显差异，这说明自由液面对耦合系统的声辐射特性影响显著。当潜深较小（H≤5R）时，随着潜深的增大，耦合系统辐射声功率特性频响曲线的峰值相应地向低频偏移，且共振响应幅值也有明显变化。该现象说明，随着潜深的增大，耦合系统的耦合模态频率相应减小，这也从侧面印证了文献[8]关于自由液面影响的结论。当潜深相对较大（H>5R）时，随着潜深的增大，耦合系统辐射声功率曲线的共峰值频率基本不变，但是共振峰值略有下降。此外，随着潜深的增大，一些高阶模态频率下的共振现象消失。这主要是因为，近水面状态下圆柱壳的弯曲模态振型与无限域中的结构模态振型存在一定的差别[11]。随着潜深的增大，近水面状态下圆柱壳的模态振型逐渐趋近于无限域中结构对应的模态振型。因而，当在激励点的位置与某一阶弯曲模态振型的周向节点重合时，该阶弯曲模态频率下的共振现象会消失。

图8自由液面对近水面状态下圆柱壳辐射声功率特性的影响

Fig.8Effect of the free surface on radiated sound power from a submerged cylindrical shell with the free surface nearby4结论

本文从理论推导角度分析了近水面状态有限长圆柱壳的输入功率流和声辐射特性，并揭示了自由液面的影响机理。通过数值计算，得到以下结论：

（1）当圆柱壳接近自由液面时，自由液面的存在将致使声场圆柱壳耦合系统的共振频率增大；

（2）随着潜深的增大，自由液面影响逐渐减弱，耦合系统的输入功率流和辐射声功率曲线的峰值频率向低频偏移；

（3）在本文研究中，当潜深H≥5R时，自由液面对水下圆柱壳输入功率流特性的影响可以忽略，但是自由液面仍然会影响耦合系统辐射声功率幅值；

本文的研究为进一步深入研究近水面条件下水下交个的声振特性提供了理论基础，也为后续工作研究多边界条件下声场圆柱壳耦合系统的振动与声辐射特性提供参考。

参考文献：

[1]Skidan O， Klosner J M， Baron M L. Sound radiation from a cylinder immersed in an acoustic fluid bounded by an elastic halfspace[J]. The Journal of the Acoustical Society of America， 1974， 56（2）： 427—439.

[2]Chang K Y， DiMaggio F L. Vibrations of cylindrical shells in a semiinfinite acoustic medium[J]. The Journal of the Acoustical Society of America， 1971， 49（3B）： 759—767.

[3]李天匀， 江丰， 叶文兵，等. 有限浸没深度无限长圆柱壳辐射声场波动特性[J]. 中国舰船研究， 2013， 8（1）：73—79.

Li Tianyun， Jiang Feng， Ye Wenbing， et al. The wave characteristics of the acoustic radiation from cylindrical shell within finite depth from the free surface[J]. 2013， 8（1）：73—79.

[4]Ye Wenbing， Li Tianyun， Zhu Xiang， et al. Acoustic radiation of cylindrical shells submerged in the fluid in presence of the seabed or dock[J]. Journal of Ship Mechanics， 2013， 17（3）： 313—325.

[5]Ergin A， Price W G， Randall R， et al. Dynamic characteristics of a sugmerged， flexible cylinder vibrating in finite water depths[J]. Journal of Ship Research， 1992， 36（2）： 154—167.

[6]王宗利， 金占禮，林启荣，等. 潜水深度对结构自振特性影响的数值分析[J]. 机械强度， 2001， 23（3）： 344—346.

Wang Zongli， Jin Zhanli， Lin Qirong， et al. Natural analysis of the influences of water depth on the vibration characteristics of submerged structures[J]. Journal of Mechanical Strength， 2001， 22（3）：344—346.

[7]刘佩， 刘书文， 黎胜. 潜深对水下圆柱壳振动声辐射特性的影响[J]. 舰船科学技术，2014，36（5）：36—41.

Liu Pei， Liu Shuwen， Li Sheng. The effect of immersion depth of submerged cylindrical shell on vibroacoustic characteristics[J]. Ship Science and Technology， 2013， 36（5）：36—41.

[8]王鹏，李天匀，朱翔，等. 近水面状态有限长圆柱壳振动特性分析[J]. 振动工程学报，2016，29（5）：772—778.

Wang Peng， Li Tianyun， Zhu Xiang， et al. Frequency analysis of submerged cylindrical shell near the fluid surface[J]. Journal of Vibration Engineering， 2016，29（5）：772—778.

[9]Zhu X， Ye W B， Li T Y， et al. The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J]. Ocean Engineering， 2013， 58： 22—26.

[10]Lee W M， Chen J T. Scattering of flexural wave in a thin plate with multiple circular holes by using the multipole Trefftz method[J]. International Journal of Solids and Structures， 2010， 47（9）： 1118—1129.

[11]郭文杰，李天匀，朱翔，等. 计及自由液面影响的水下有限深度圆柱壳自由振动分析[J]. 振动与冲击， 2017，36（10）：1—6.

Guo Wenjie， Li Tianyun， Zhu Xiang， et al. Free vibration analysis of a submerged cylindrical shell with finite depth from the free surface[J]. Journal of Vibration and Shock， 2017，36（10）：1—6.

Research on input power flow and sound radiation from

a cylindrical shell immersed near the free surface

WANG Peng， LI Tianyun， ZHU Xiang， GUO Wenjie

（School of Naval Architecture and Ocean Engineering， Huazhong University of Science and

Technology， Wuhan 430074， China）

Abstract： The soundstructure interaction model is used to analyze the input power flow and sound radiation characteristics from a cylindrical shell immersed in fluid near the free surface， and the effect of free surface is considered. The accuracy of present method is verified through comparison with the FEM. When cylindrical shell is close to free surface， the existence of free surface will result in the reduction of resonance frequencies. When the immersion depth of shell increases， the influence of free surface will be reduced. Finally， the free surface effect on structure vibration characteristics is negligible， but it will still affect the response level of sound radiation characteristics of coupled system. Key words： vibration of ship； cylindrical shell immersed near the free surface； free surface； input power flow； the image method作者簡介： 王鹏（1989—），男，博士研究生。Email：paulwang@hust.edu.cn

通讯作者： 李天匀（1969—），男，博士，教授，博士生导师。Email：ltyz801@hust.edu.cn