数形结合思想在小学数学教学中的应用
陈劲松
数形结合思想概括来讲就是抽象与具体的相互转化。在小学阶段学生刚开始接触数学的时候,老师应该把数学中最精彩的思想方法,数形结合的思想慢慢渗透给学生,这样在他们以后的学习中就能轻松地从具体中提炼出抽象,从抽象中描绘出具体。在小学数学教学中加强数形结合思想的运用,既能提高学生对知识的理解,又能激发学生学习数学的兴趣。如果能在小学阶段将数形结合的思想深植于学生的学习习惯中,将对他们以后进入初高中进行数学学习打下良好的基础。
一、利用数形结合思想在小学数学教学中讲解定义、定理、运算法则(数到形)
二、利用数形结合思想解答小学数学教学中遇到的问题(形到数)
比如,有这样一个问题,2条直线相交最多有几个交点?3条直线相交最多有几个交点?4条直线相交最多有几个交点?2017条直线相交最多有几个交点?n条直线相交最多有几个交点?这些问题由浅入深,由特殊到一般,不仅考查了学生归纳总结的能力,更重要的是将几何问题和代数问题结合起来,锻炼学生使用数形结合思想解决问题的能力。首先在教学过程中,老师可以先画出两条直线相交时的图形(如图3),然后提问学生如果要画第三条直线,怎样画才能使得交点数最多,这就要使得第三条直线和我们已经画完的两条直线都相交(如图4),这样的话交点数就是1+2个,再画第四条直线时,要使得交点数最多,就要使得第四条直线和前面我们画的三条直线也全都相交(如图5),因此交点数为1+2+ 3。以此类推,如果有2017条直线相交,那么第2017条直线就要和前面我们画的2016条直线全都相交,交点数为1+2+ 3+4+…+2016,归纳总结得n条直线就有1+2+3+4+…+(n-1)个交点。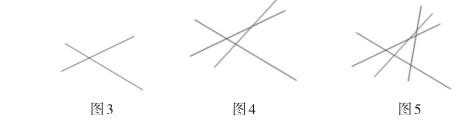
三、数形结合思想在小学数学教学中的应用
在小學数学教学中,有一部分内容是统计。统计不仅是收集数据还要对数据进行整理和描述。数据的收集和整理都是对数字的抽象处理,而将数据描述出来就是将抽象转化为具体,让使用数据的人能够清楚直观地了解数据的分布、各部分数据所占总体的比例以及数据的整体走向等。书中向学生们介绍了三种统计图表,分别是饼图、直方图和折线图,画出统计图是从数到形的具体化,看得懂统计图并能通过看统计图回答一些简单的数据问题,则是由形到数的抽象化,因此这一章的内容是数形结合思想中互相转化的一个典型例子。
在小学数学教学中,类似典型的问题还有行程问题、追赶问题、位置和方向问题等。除了这些常考常见的题型外,教师们在教学过程中可以有针对性地设置一些专题讲解,用于完善学生的解题技巧。可以看出在小学数学教学中,数形结合思想解决问题是一种常见且重要的方法,是为以后初高中学习函数、解析几何等更高层次的数形结合的应用打基础,只有把基础夯实,在以后的学习中才能事半功倍。
作者单位江苏省滨海县蔡桥镇中心小学

